概要信息：

　目　　录　
第一章　绪论 （１）
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
第二章　连续时间系统的时域分析 （１０）
!!!!!!!!!!!!!!!!!!!!!!!!!
第三章　傅里叶变换 （２６）
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
第四章　拉普拉斯变换、连续时间系统的Ｓ域分析 （４９）
!!!!!!!!!!!!!!!!!!!
第五章　傅里叶变换应用于通信系统－滤波、调制与抽样 （７８）
!!!!!!!!!!!!!!!!
第六章　信号的空间矢量分析 （９５）
!!!!!!!!!!!!!!!!!!!!!!!!!!!
第七章　离散信号与系统时域分析 （１１６）
!!!!!!!!!!!!!!!!!!!!!!!!!
第八章　Ｚ变换和离散时间系统的Ｚ域分析 （１３１）
!!!!!!!!!!!!!!!!!!!!!
第九章　离散傅里叶变换及其他离散正交变换 （１５１）
!!!!!!!!!!!!!!!!!!!!
第十一章　反馈系统 （１６５）
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
第十二章　系统的状态变量分析 （１７９）
!!!!!!!!!!!!!!!!!!!!!!!!!!
第一章　绪　　论
一、信号的概念和分类
１．信号
随时间变化的物理量，消息的具体表现形式。
２．描述和分类
（１）描述：波形图和函数表达式
（２）分类：确定和随机
周期和非周期
连续和离散（注意区别模拟和数字）
一维和多维
要点：判定离散时间信号是否为数字信号
例１　判断下列图示信号的类型
（ａ）连续（模拟）；（ｂ）连续（量化）；（ｃ）离散（数字）；（ｄ）离散；（ｅ）离散（数字）；（ｆ）离散（数字）
二、典型非奇异信号
１．指数信号
ｆ（ｔ）＝Ｋｅａｔ，τ＝ １
ａ
—１—
郑君里《信号与系统》考点精讲
２．正弦信号
ｆ（ｔ）＝Ｋｓｉｎ（ωｔ＋θ）
３．复指数信号
ｆ（ｔ）＝Ｋｅｓｔ＝Ｋｅωｔｃｏｓ（ωｔ）＋ｊＫｅσｔｓｉｎ（ωｔ）
４．抽样信号
Ｓａ（ｔ）＝ｓｉｎｔｔ
５．钟形信号
ｆ（ｔ）＝Ｅｅ－（
ｔ
τ）
２
要点：熟记典型信号的表达式、波形特征
三、信号的运算
关于自变量：位移、反折、尺度
关于信号的幅值：加、乘（在相同时刻）、微分、积分
位移：时间轴上左右平移
ｆ（ｔ） →
移位
ｆ（ｔ）＝ｆ（ｔ＋ｔ０）
反折：时间轴上关于纵轴镜像
ｆ（ｔ） →
反折
ｆ（ｔ）＝ｆ（－ｔ）
尺度：时间轴上的压缩和扩展
ｆ（ｔ） →
尺度
ｆ（ｔ）＝ｆ（ａｔ）
相加
ｆ１（ｔ）、ｆ２（ｔ） →
相加
ｆ（ｔ）＝ｆ１（ｔ）＋ｆ２（ｔ）
相乘
ｆ１（ｔ）、ｆ２（ｔ） →
相乘
ｆ（ｔ）＝ｆ１（ｔ）×ｆ２（ｔ）
微分
ｆ（ｔ） →
微分 ｄ
ｄｔｆ（ｔ）
积分
ｆ（ｔ） →
积分∫
ｔ
－
!
ｆ（ｔ）ｄｔ
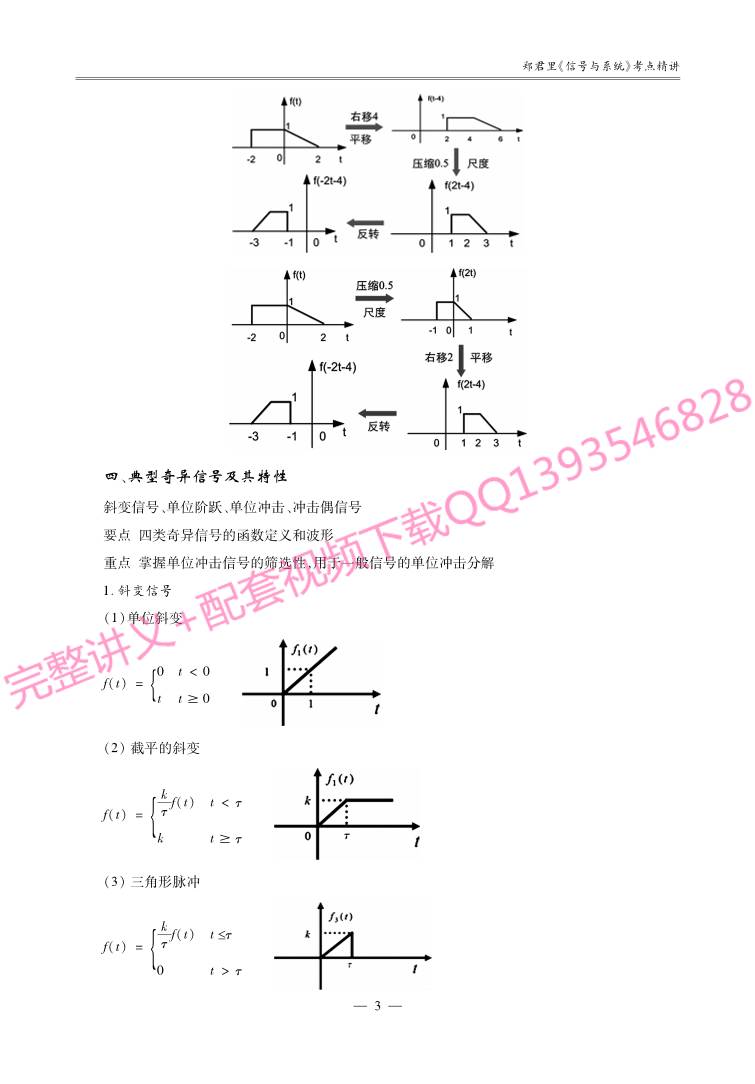
掌握用上述运算进行信号波形变换的方法
（图见视频）
例２　已知ｆ（ｔ），求ｆ（－４－２ｔ）
—２—
四、典型奇异信号及其特性
斜变信号、单位阶跃、单位冲击、冲击偶信号
要点：四类奇异信号的函数定义和波形
重点：掌握单位冲击信号的筛选性，用于一般信号的单位冲击分解
１．斜变信号
（１）单位斜变
ｆ（ｔ）＝
０ ｔ＜０
ｔ ｔ{ ０
　　
（２）截平的斜变
ｆ（ｔ）＝
ｋ
τ
ｆ（ｔ） ｔ＜τ
ｋ ｔ
{
τ
　　
（３）三角形脉冲
ｆ（ｔ）＝
ｋ
τ
ｆ（ｔ） ｔ
"τ
０ ｔ＞
{
τ
　　
—３—
郑君里《信号与系统》考点精讲
２．单位阶跃信号
（１）单位阶跃
ｕ（ｔ）＝
０ ｔ＜０
１ ｔ＞{ ０
　　
（２）矩形脉冲
ＲＴ（ｔ）＝ｕ（ｔ）－ｕ（ｔ－Ｔ）　　
（３）符号函数
ｓｇｎ（ｔ）＝
１ ｔ＞０
－１ ｔ＜{ ０
　　
用来描述符号函数：ｓｇｎ（ｔ）＝２ｕ（ｔ）－１
描述信号的接入特性：ｆ（ｔ）＝ｆ１（ｔ）ｕ（ｔ）
３．单位冲激信号（６种来源）
（１）矩形脉冲
δ（ｔ）＝ｌｉｍ
τ→０
１
τ
［ｕ（ｔ＋τ２）－ｕ（ｔ－
τ
２）］　　
（２）三角脉冲
δ（ｔ）＝ｌｉｍ
τ→０
１
τ
１
τ
（１－ ｔ
τ
）［ｕ（ｔ＋τ）－ｕ（ｔ－τ２{ }）］　　
（３）双边指数脉冲
δ（ｔ）＝ｌｉｍ
τ→０
１
２τ
ｅ－
ｔ{ }τ 　　
（４）钟形脉冲
δ（ｔ）＝ｌｉｍ
τ→０
１
τ
ｅ－π（
ｔ
τ）{ }２ 　　
—４—
（５）采样信号
δ（ｔ）＝ｌｉｍ
ｋ→!
ｋ
π
Ｓａ（ｋｔ{ }）　　
（６）狄拉克函数
∫
!
－
!
δ（ｔ）ｄｔ＝１
δ（ｔ）＝０（当ｔ≠０
{
）
　　
４．冲击偶信号及其演变
δ′（ｔ）＝ｄｄｔδ（ｔ）＝
ｄ２
ｄｔ２
ｕ（ｔ）
（图见视频）
５．单位冲激信号的性质
（１）抽样性
∫
!
－
!
δ（ｔ）ｆ（ｔ）ｄｔ＝∫
!
－
!
δ（ｔ）ｆ（０）ｄｔ＝ｆ（０）∫
!
－
!
δ（ｔ）ｄｔ＝ｆ（０）
∫
!
－
!
δ（ｔ－ｔ０）ｆ（ｔ）ｄｔ＝∫
!
－
!
δ（ｔ－ｔ０）ｆ（ｔ０）ｄｔ＝ｆ（ｔ０）
（２）偶对称性
δ（ｔ）＝δ（－ｔ）
（３）尺度变换
δ（ａｔ）＝ １
ａδ（ｔ）
６．冲激偶信号的性质
（１）抽样性
∫
!
－
!
δ′（ｔ）ｆ（ｔ）ｄｔ＝－ｆ′（０）
（２）乘法
ｆ（ｔ）δ′（ｔ）＝ｆ（０）δ′（ｔ）－ｆ′（０）δ（ｔ）
（３）积分
∫
!
－
!
δ′（ｔ）ｄｔ＝０
（４）尺度
δ′（ａｔ）＝ １
ａ·
１
ａδ′（ｔ）
（５）卷积
—５—
郑君里《信号与系统》考点精讲
ｆ（ｔ）δ′（ｔ）＝ｄｄｔｆ（ｔ）＝ｆ′（ｔ）
例３　求列下表达式的值
（１）∫
!
－
!
ｆ（ｔ０－ｔ）δ（ｔ）ｄｔ
（２）∫
!
－
!
ｅ－ｊωｔ［δ（ｔ）－δ（ｔ－ｔ０）］ｄｔ
解：根据单位冲激信号的筛选性可得：
∫
!
－
!
ｆ（ｔ０－ｔ）δ（ｔ）ｄｔ＝－∫
!
－
!
ｆ（ｔ０－ｔ）δ（－ｔ）ｄ（－ｔ）
＝－∫
－
!
!
ｆ（ｔ０＋τ）？δ（τ）ｄτ＝∫
!
－
!
ｆ（ｔ０＋τ）δ（τ）ｄτ
＝∫
!
－
!
ｆ（ｔ）？δ（ｔ－ｔ０）ｄｔ＝ｆ（ｔ０）
∫
!
－
!
ｅ－ｊωｔ［δ（ｔ）－δ（ｔ－ｔ０）］ｄｔ＝∫
!
－
!
ｅ－ｊωｔδ（ｔ）ｄｔ－∫
!
－
!
ｅ－ｊωｔδ（ｔ－ｔ０）ｄｔ＝１－ｅ
ｊωｔ０
五、信号的分解
直流分量与交流分量、奇分量与偶分量、脉冲分量、阶跃分量、正交分量
重点：掌握信号的单位冲击分解
１．交流分量与直流分量
ｆ（ｔ）→ｆＤ ＋ｆＡ（ｔ）
Ｐ＝１Ｔ∫
Ｔ
２
－Ｔ２
ｆ２（ｔ）ｄｔ
＝１Ｔ∫
Ｔ
２
－Ｔ２
［ｆＤ ＋ｆＡ（ｔ）］
２ｄｔ
＝１Ｔ∫
Ｔ
２
－Ｔ２
［ｆ２
Ｄ
＋２ｆＤｆＡ（ｔ）＋ｆ
２
Ａ（ｔ）］ｄｔ
＝ｆ２Ｄ ＋
１
Ｔ∫
Ｔ
２
－Ｔ２
ｆ２Ａ（ｔ）ｄｔ
信号的功率 ＝直流功率 ＋交流功率
直流功率 ＝ｆ２Ｄ
交流功率 ＝１Ｔ∫
Ｔ
２
－Ｔ２
ｆ２Ａ（ｔ）ｄｔ
２．奇分量和偶分量
ｆ（ｔ）→ｆｅ（ｔ）＋ｆｏ（ｔ）＝
１
２［ｆ（ｔ）＋ｆ（－ｔ）］＋
１
２［ｆ（ｔ）－ｆ（－ｔ）］ａ
３．正交分量
用相互正交的正交函数集各个分量的线性组合来表示某些信号
—６—
注意：只用于周期信号的分解，常见的正交完备集就是三角函数和复指数函数，即周期信号的三
角级数分解和复指数分解。
４．脉冲分量
→　 　ｆ（ｔ）＝ｌｉｍ
τ→０
ｆ１（ｔ）＝∫
!
－
!
ｆ（τ）δ（ｔ－τ）ｄτ
六、系统模型及其分类
重点：掌握系统的分类
１．系统模型的表示方法：数学方程和框图
连续时间系统的描述：微分方程
离散时间系统的描述： }
→
差分方程
选取合适的状态变量，如电容电压、电感电流等
框图表示系统的基本运算单元：
加法　　
乘法　　
积分　　
例４　求解下列ＲＬＣ串联电路并画出系统框图
解：根据ＫＶＬ可得：
ｉ（ｔ）＝Ｃ
ｄｕｃ（ｔ）
ｄｔ
ｕｃ（ｔ）＋Ｌ
ｄｉ（ｔ）
ｄｔ ＋Ｒｉ（ｔ）＝ｅ（ｔ
{
）
整理可得该系统的微分方程为：ＬＣｄ
２ｉ（ｔ）
ｄｔ２
＋ＲＣｄｉ（ｔ）ｄｔ ＋ｉ（ｔ）＝Ｃ
ｄｅ（ｔ）
ｄｔ
对上式积分：ｉ（ｔ）＝１Ｌ∫ｅ（τ）ｄτ－ＲＬ∫ｉ（τ）ｄτ－１ＬＣｉ（τ）ｄτｄτ
—７—
郑君里《信号与系统》考点精讲
利用框图的基本运算单元得：
２．系统的分类
１）连续时间系统、离散时间系统———输入输出信号类型
２）即时系统、动态系统———有无储能元件
３）集总参数、分布参数———状态变量手否考虑空间位置因素
４）线性系统、非线性系统———是否满足线性特性
５）时不变系统、时变系统———是否具有时不变特性
６）因果系统、非因果系统———响应与激励施加的先后关系
７）稳定系统、非稳定系统———系统响应的收敛性
８）可逆系统、不可逆系统———响应与激励是否具有
一一对应的关系
重点研究：稳定的线性时不变系统因果系统
Ｎ阶连续ＬＴＩ系统
　描述
→
　
Ｎ阶常系数线性微分方程
Ｎ阶离散ＬＴＩ系统
　描述
→
　
Ｎ阶常系数线性差分方程
七、系统模型及其分类
重点：线性时不变系统的判定
１．线性时不变系统的特点：
１）线性性质：叠加性、均匀性（齐次性）
２）时不变性：响应与激励施加的时刻无关
３）微分特性：本质即线性
２．线性性质的判定：
分解性、零状态线性、零输入线性
３．时不变特性的判定：
激励信号平移，判定响应
例５　试判定下述系统的线性特性、时变特性ｒ（ｔ）＝ｘ（０－）ｓｉｎｔ＋ｔｅ（ｔ）
解：（１）满足分解性，易知：
ｒｚｉ（ｔ）＝ｘ（０－）ｓｉｎｔ　　ｒｚｓ（ｔ）＝ｔｅ（ｔ）
（２）ｘ（０－）＝ｘ１（０－）时ｒｚｉ１（ｔ）＝ｘ１（０－）ｓｉｎｔ，
ｘ（０－）＝ｘ２（０－）时，ｒｚｉ２（ｔ）＝ｘ２（０－）ｓｉｎｔ
—８—
当ｘ（０－）＝ａｘ１（０－）＋ｂｘ２（０－）
ｒｚｉ（ｔ）＝［ａｘ１（０－）＋ｂｘ２（０－）］ｓｉｎｔ
＝ａｘ１（０－）ｓｉｎｔ＋ｂｘ２（０－）ｓｉｎｔ
＝ａｒｚｉ１（ｔ）＋ｂｒｚｉ２（ｔ）
（３）ｅ（ｔ）＝ｅ１（ｔ）时，ｒｚｓ１（ｔ）＝ｔｅ１（ｔ）
ｅ（ｔ）＝ｅ２（ｔ）时，ｒｚｓ２（ｔ）＝ｔｅ２（ｔ）
当ｅ（ｔ）＝ａｅ１（ｔ）＋ｂｅ２（ｔ）时，
ｒｚｓ（ｔ）＝ｔ［ａｅ１（ｔ）＋ｂｅ２（ｔ）］＝ａｔｅ１（ｔ）＋ｂｔｅ２（ｔ）＝ａｒｚｓ１（ｔ）＋ｂｒｚｓ２（ｔ）
满足零输入线性，综合（１）～（３），该系统为线性系统
关于时变特性的判断：当ｅ（ｔ）→ｅ（ｔ－ｔ０）时
系统响应ｙ（ｔ）＝ｘ（０－）ｓｉｎｔ＋ｔｅ（ｔ－ｔ０）
而ｒ（ｔ－ｔ０）＝ｘ（０－）ｓｉｎ（ｔ－ｔ０）＋（ｔ－ｔ０）ｅ（ｔ－ｔ０）≠ｙ（ｔ）
因此，该系统为时变系统
八、系统分析的方法
１．系统研究的内容
系统分析：给定系统在特定激励下的响应
系统综合：满足响应与激励之间关系的系统设计及实现
２．ＬＴＩ系统分析的方法
１）数学描述：输入—输出描述法，适用于单变量系统
状态变量描述法，适用于多变量系统
２）模型求解：时域求解法（经典法、卷积法、数值解法）
变换域求解法（ＬＴ、ＦＴ、ＺＴ）
→ →时域卷积 频域乘积 频域代数方程
→ →频域卷积 时域乘积 时域代数方程
—９—
郑君里《信号与系统》考点精讲
第二章　连续时间系统的时域分析
ＬＴＩ系统分析的方法：
数学描述：输入—输出描述法，适用于单变量系统
状态变量描述法，适用于多变量系统
模型求解：时域求解法（经典法、卷积法、数值解法）
变换域求解法（ＬＴ、ＦＴ、ＺＴ）
→ →时域卷积 频域乘积 频域代数方程
经典法：解微分方程，齐次通解＋非齐次特解
自由响应＋强迫响应
注意初始值０＋、０－的区别与求法
卷积法：求卷积运算，零状态响应，物理概念明确。
一、微分方程的建立与求解
１．微分方程的建立
根据系统的物理模型、元件的约束特性、系统结构的
约束特性：ＫＶＬ、ＫＣＬ、欧姆定理、达朗贝尔原理。
对于机械系统的处理：机电类比法。
例１　列出下述两个系统的微分方程
对于第一个系统，选取ｖ（ｔ）为变量，可得元件的电流关系：
ｉＲ（ｔ）＝
１
Ｒｖ（ｔ）　　ｉＬ（ｔ）＝
１
Ｒ∫
ｔ
－
!
ｖ（τ）ｄτ　　ｉＣ（ｔ）＝Ｃ
ｄ
ｄｔｖ（ｔ）
根据ＫＣＬ：ｉＲ（ｔ）＋ｉＬ（ｔ）＋ｉＣ（ｔ）＝ｉＳ（ｔ）
整理得：Ｃｄ
２
ｄｔ２
ｖ（ｔ）＋１Ｒ
ｄ
ｄｔｖ（ｔ）＋
１
Ｌｖ（ｔ）＝
ｄ
ｄｔｉＳ（ｔ）
对于第二个系统，选取ｖ（ｔ）为变量，根据胡克定律：
Ｆｋ（ｔ）＝ｋ·ｘ（ｔ）＝ｋ∫
ｔ
－
!
ｖ（τ）ｄτ
摩擦力：Ｆｆ（ｔ）＝ｆ·ｖ（ｔ）　　ｆ：摩擦系数
—０１—
惯性力：Ｆｍ（ｔ）＝ｍ·
ｄ
ｄｔｖ（ｔ）　　惯性定律
力学平衡的达郎贝尔原理：Ｆｋ（ｔ）＋Ｆｆ（ｔ）＋Ｆｍ（ｔ）＝ＦＳ（ｔ）
整理得：ｍｄ
２
ｄｔ２
ｖ（ｔ）＋ｆｄｄｔｖ（ｔ）＋ｋｖ（ｔ）＝
ｄ
ｄｔＦＳ（ｔ）
分析形式： →机械量 电气量（机电类比法）
２．微分方程的求解
线性时不变系统（ＬＴＩ）以常系数线性微分方程描述：
设系统激励为ｅ（ｔ），响应为ｒ（ｔ），则系统可描述为：
Ｃ０
ｄｎ
ｄｔｎ
ｒ（ｔ）＋Ｃ１
ｄｎ－１
ｄｔｎ－１
ｒ（ｔ）＋… ＋Ｃｎ－１
ｄ
ｄｔｒ（ｔ）＋Ｃｎｒ（ｔ）
＝Ｅ０
ｄｍ
ｄｔｍ
ｅ（ｔ）＋Ｅ１
ｄｍ－１
ｄｔｍ－１
ｅ（ｔ）＋… ＋Ｅｍ－１
ｄ
ｄｔｅ（ｔ）＋Ｅｍｅ（ｔ）
根据经典法：全响应 ＝齐次通解 ＋非其次特解
Ｃ０
ｄｎ
ｄｔｎ
ｒ（ｔ）＋Ｃ１
ｄｎ－１
ｄｔｎ－１
ｒ（ｔ）＋… ＋Ｃｎ－１
ｄ
ｄｔｒ（ｔ）＋Ｃｎｒ（ｔ）＝０
齐次解形如Ａｅαｔ的线性组合，设ｒ（ｔ）＝Ａｅαｔ则：
Ｃ０Ａα
ｎｅαｔ＋Ｃ１Ａα
ｎ－１ｅαｔ＋… ＋Ｃｎ－１Ａαｅα
ｔ＋ＣｎＡｅα
ｔ＝０
得特征方程：Ｃ０α
ｎ＋Ｃ１α
ｎ－１＋… ＋Ｃｎ－１α＋Ｃｎ ＝０
若αｋ满足上式，则Ａｅαｋ
ｔ满足原方程
１）无重根ｒｈ（ｔ）＝∑
ｎ
ｉ＝１
Ａｉｅαｉ
ｔ
２）α１有ｋ重根ｒｈ（ｔ）＝（∑
ｋ
ｉ＝１
Ａｉｔ
ｋ－ｉ
）·ｅα１ｔ＋∑
ｎ－ｋ＋１
ｉ＝２
Ａｉｅαｉ
ｔ
特解ｒｐ（ｔ）形式取决于激励信号
选定形式，待定系数法
齐次解只与系统本身的结构和参数有关，而与激励信号无关，反映系统本身特征，又称为固有相
应或自由响应。而特解的形式由激励决定，称为强迫响应。
激励ｅ（ｔ） 响应特解ｒｐ（ｔ）
常数Ｅ 常数Ｂ
ｔｐ Ｂ１ｔ
ｐ＋Ｂ２ｔ
ｐ－１＋… ＋Ｂｐｔ＋Ｂｐ＋１
ｅαｔ Ｂｅαｔ
ｃｏｓωｔ
ｓｉｎωｔ
Ｂ１ｃｏｓωｔ＋Ｂ２ｓｉｎωｔ
ｔｐ·ｅαｔ·ｃｏｓωｔ
ｔｐ·ｅαｔ·ｓｉｎωｔ
（Ｂ１ｔ
ｐ＋Ｂ２ｔ
ｐ－１＋… ＋Ｂｐｔ＋Ｂｐ＋１）ｅα
ｔｃｏｓωｔ
＋（Ｄ１ｔ
ｐ＋Ｄ２ｔ
ｐ－１＋… ＋Ｄｐｔ＋Ｄｐ＋１）ｅα
ｔｓｉｎωｔ
—１１—
郑君里《信号与系统》考点精讲
这样，原方程的完全解为：
ｒ（ｔ）＝ｒｈ（ｔ）＋ｒｐ（ｔ）＝∑
ｎ
ｉ＝１
Ａｉｅ
－αｉｔ＋ｒｐ（ｔ）
为使方程有唯一解，需根据初始状态求解待定系数：
设求解区为：０＋"ｔ＜＋!
初始状态为：ｒ（０＋）ｒ
、（０＋）ｒ
（ｎ－１）（０＋）
则：
ｒ（０＋）＝Ａ１＋Ａ２＋…Ａｎ＋ｒｐ（０＋）
ｒ、（０＋）＝Ａ１α１＋Ａ２α２＋…Ａｎαｎ＋ｒ
、
ｐ（０＋）
……
ｒ（ｎ－１）（０＋）＝Ａ１α
ｎ－１
１ ＋Ａ２α
ｎ－１
２ ＋…Ａｎ＋ｒ
ｎ－１
ｐ （０＋







）
以矩阵形式表示为：
［
ｒ（０＋）－ｒｐ（０＋）
ｒ、（０＋）－ｒ
、
ｐ（０＋）

ｒ（ｎ－１）（０＋）－ｒ
ｎ－１
ｐ （０＋）
］＝［
１ １ … １
α１ α２ … αｎ
   
αｎ－１１ αｎ－１２ … αｎ－１２
］［
Ａ１
Ａ２

Ａｎ
］
例２　给定微分方程：ｄ
２
ｄｔ２
ｒ（ｔ）＋５ｄｄｔｒ（ｔ）＋６ｒ（ｔ）＝ｅ（ｔ）
求：（１）ｅ（ｔ）＝２ｅ－ｔ，ｔ０，ｒ（０）＝２，ｒ′（０）＝－１
（２）ｅ（ｔ）＝ｅ－２ｔ，ｔ０，ｒ（０）＝１，ｒ′（０）＝０
时系统的全响应。
解：原系统的特征方程为：λ２＋５λ＋６＝０
求得特征根：λ１ ＝－２　　λ２ ＝－３
齐次通解为：ｒｈ（ｔ）＝Ｃ１ｅ
－２ｔ＋Ｃ２ｅ
－３ｔ
根据激励形式可知：
（１）ｅ（ｔ）＝２ｅ－ｔ时，特解为：ｒｐ（ｔ）＝Ａｅ
－ｔ
将特解带入原方程得：
Ａｅ－ｔ＋５（－Ａｅ－ｔ）＋６Ａｅ－ｔ＝２Ａｅ－ｔ
解得：Ａ＝１
可得特解为：ｒｐ（ｔ）＝ｅ
－ｔ
系统全响应：ｒ（ｔ）＝ｒｈ（ｔ）＋ｒｐ（ｔ）＝Ｃ１ｅ
－２ｔ＋Ｃ２ｅ
－３ｔ＋ｅ－ｔ
现根据初始状态求待定系数Ｃ１、Ｃ２：
ｒ（０）＝Ｃ１＋Ｃ２＋１＝２　　ｒ′（０）＝－２Ｃ１－３Ｃ２－１＝－１
解得：Ｃ１ ＝３、Ｃ２ ＝－２
—２１—
故全响应为：ｒ（ｔ）＝３ｅ－２ｔ－２ｅ－３ｔ＋ｅ－ｔ
（２）ｅ（ｔ）＝ｅ－２ｔ时，其指数次与特征跟之一相同：
其特解形式为：ｒｐ（ｔ）＝（Ａ１ｔ＋Ａ０）ｅ
－２ｔ
带入微分方程：Ａ１ｅ
－２ｔ＝ｅ－２ｔ
解得：Ａ１ ＝１
系统全响应：
ｒ（ｔ）＝ｒｈ（ｔ）＋ｒｐ（ｔ）＝Ｃ１ｅ
－２ｔ＋Ｃ２ｅ
－３ｔ＋（ｔｅ－２ｔ＋Ａ０ｅ
－２ｔ）
＝（Ｃ１＋Ａ０）ｅ
－２ｔ＋Ｃ２ｅ
－３ｔ＋ｔｅ－２ｔ
代入初始条件得：
ｒ（０）＝（Ｃ１＋Ａ０）＋Ｃ２ ＝１
ｒ′（０）＝－２（Ｃ１＋Ａ０）－３Ｃ２＋１＝０
解得：Ｃ１＋Ａ０ ＝２　　Ｃ２ ＝－１
故全响应为：ｒ（ｔ）＝２ｅ－２ｔ－ｅ－３ｔ＋ｔｅ－２ｔ
利用初始条件无法求出Ｃ１和Ａ０，因此分解不出自由响应和强迫响应。
二、起始点的跳变———从０－到０＋状态的转换
１．关于０－状态和０＋状态
状态为零输入时的初始状态，即初始值由系统的初始储能所产生。
０＋状态为加入激励信号后的初始状态，即初始值不但有初始储能，还受激励信号的影响。
系统０－状态 } →
系统激励信号
０＋状态
０＋状态
齐次通解{ } →
非齐次特解
全响应
０－到０＋ →跃变 右边包含δ（ｔ）及其各阶导数
２．０＋状态的确定———冲激函数匹配法
冲激函数匹配法：利用ｔ＝０时刻方程两边的δ（ｔ）及各阶导数应该平衡的原理来求解（０＋）的方
法。原因在于微分方程右边还有δ（ｔ）及其各阶导数，造成（０＋）和（０－）时刻的值不相等。
在经典法求全响应的积分常数时，用的是０＋状态初始值。
在求系统零输入响应时，用的是０－状态初始值。
在求系统零状态响应时，用的是０＋状态初始值，这时的零状态是指０－状态为零。
已知系统为：
ａ０ｙ（ｔ）＋ａ１ｙ′（ｔ）＋… ＋ａｎｙ
（ｎ）（ｔ）＝ｂ０＋ｂ１δ（ｔ）＋ｂ２δ′（ｔ）＋… ＋ｂｍδ
（ｍ－１）（ｔ）Ｑ
若ｍ
"
ｎ则可设：
—３１—
郑君里《信号与系统》考点精讲
ｙ（ｎ）（ｔ）＝Ｃｍδ
（ｍ－１）（ｔ）＋… ＋Ｃ１δ（ｔ）＋Ｃ０
ｙ（ｎ－１）（ｔ）＝Ｃｍδ
（ｍ－２）（ｔ）＋… ＋Ｃ２δ（ｔ）＋Ｃ１
　　　
ｙ（ｎ－ｍ）（ｔ）＝Ｃｍ
ｙ（ｎ－ｍ－１）（ｔ）＝… ＝ｙ（ｔ）＝０
若ｍ＞ｎ则可设：
ｙ（ｎ）（ｔ）＝Ｃｍδ
（ｍ－１）（ｔ）＋… ＋Ｃ１δ（ｔ）＋Ｃ０
ｙ（ｎ－１）（ｔ）＝Ｃｍδ
（ｍ－２）（ｔ）＋… ＋Ｃ２δ（ｔ）＋Ｃ１
　　　
ｙ（ｔ）＝Ｃｍδ
（ｍ－ｎ－１）（ｔ）＋… ＋Ｃｎ－１
将ｙ（ｔ）及其各阶导数带入原方程，求出Ｃ０…Ｃｍ对ｙ（ｔ）及各阶导数求（０－，０＋）的积分．
例３　电路如图示，ｔ＜０时Ｓ处于位置１且已达到稳态，ｔ＝０时，Ｓ由１转向２。建立ｉ（ｔ）的微分
方程并求解其在ｔ０＋时的变化。
解：１）列写电路方程
根据ＫＶＬ：Ｒ１ｉ（ｔ）＋ｖＣ（ｔ）＝ｅ（ｔ）
ＬｄｄｔｉＬ（ｔ）＋ｉＬ（ｔ）Ｒ２ ＝ｖＣ（ｔ）
根据ＫＣＬ：ＣｄｄｔｖＣ（ｔ）＋ｉＬ（ｔ）２ ＝ｉ（ｔ）
先消去ｖＣ（ｔ）得：
ｄ
ｄｔｉ（ｔ）＝－
１
Ｒ１Ｃ
ｉ（ｔ）＋ １Ｒ１Ｃ
ｉＬ（ｔ）＋
１
Ｒ１
ｄ
ｄｔｅ（ｔ）
ｄ
ｄｔｉＬ（ｔ）＝－
Ｒ１
Ｌｉ（ｔ）－
Ｒ２
ＬｉＬ（ｔ）＋
１
Ｌｅ（ｔ）
再消去ｉＬ（ｔ）得：
ｄ
ｄｔｉＬ（ｔ）＝－
Ｒ１
Ｌｉ（ｔ）－
Ｒ２
ＬｉＬ（ｔ）＋
１
Ｌｅ（ｔ）
ｄ２
ｄｔ２
ｉ（ｔ）＋（１Ｒ１Ｃ
＋
Ｒ２
Ｌ）
ｄ
ｄｔｉ（ｔ）＋（
１
ＬＣ＋
Ｒ２
Ｒ１ＬＣ
）ｉ（ｔ）
＝１Ｒ１
ｄ２
ｄｔ２
ｅ（ｔ）＋
Ｒ２
Ｒ１Ｌ
ｄ
ｄｔｅ（ｔ）＋
１
Ｒ１ＬＣ
ｅ（ｔ）
—４１—
带入参数得：
ｄ２
ｄｔ２
ｉ（ｔ）＋７ｄｄｔｉ（ｔ）＋１０ｉ（ｔ）＝
ｄ２
ｄｔ２
ｅ（ｔ）＋６ｄｄｔｅ（ｔ）＋４ｅ（ｔ）
２）求系统全响应
齐次解：
特征方程为：λ２＋７λ＋１０＝０
特征根：λ１ ＝－２　　λ２ ＝－５
可得：ｉｈ（ｔ）＝Ａ１ｅ
－２ｔ＋Ａ２ｅ
－５ｔ（ｔ０＋）
由题设知：ｔ０＋时，ｅ（ｔ）＝４Ｖ为常数，
故特解形式为：ｉｐ（ｔ）＝Ｂ
带入系统方程解得：Ｂ＝８５
因此：ｔ０＋时，
ｉ（ｔ）＝ｉｈ（ｔ）＋ｉｐ（ｔ）＝Ａ１ｅ
－２ｔ＋Ａ２ｅ
－５ｔ＋８５
３）确定换路后的ｉ（０＋）和
ｄ
ｄｔｉ（０＋）
换路前：ｉ（０－）＝ｉＬ（０－）＝
２
Ｒ１＋Ｒ２
＝４５Ａ
ｄ
ｄｔｉ（０－）＝０
ｖＣ（０－）＝ｉＬ·Ｒ２ ＝
４
５×
３
２ ＝
６
５Ｖ
换路后，根据换路定理：
ｉ（０＋）＝
１
Ｒ１
［ｅ（０＋）－ｖＣ（０＋）］＝
１
Ｒ１
［ｅ（０＋）－ｖＣ（０－）］＝
１
１［４－
６
５］＝
１４
５　　Ａ
ｄ
ｄｔｉ（０＋）＝
１
Ｒ１
［
ｄ
ｄｔｅ（０＋）－
ｄ
ｄｔｖＣ（０＋）］
＝１Ｒ１
ｄ
ｄｔｅ（０＋）－
１
Ｃ［ｉ（０＋）－ｉＬ（０＋{ }）］
＝１Ｒ１
ｄ
ｄｔｅ（０＋）－
１
Ｃ［ｉ（０＋）－ｉＬ（０－{ }）］
＝１１［０－
１
１（
１４
５－
４
５）］＝－２　　Ａ／ｓ
４）求ｉ（ｔ）在ｔ０＋时的全响应：
根据ｉ（ｔ）的全响应表达式可得：
ｉ（０＋）＝Ａ１＋Ａ２＋
８
５ ＝
１４
５
ｄ
ｄｔｉ（０＋）＝－２Ａ１－５Ａ２ ＝－
{ ２
—５１—
郑君里《信号与系统》考点精讲
解得：Ａ１ ＝
４
３　Ａ２ ＝－
２
１５
系统全响应为：
ｉ（ｔ）＝（４３ｅ
－２ｔ－２１５ｅ
－５ｔ＋８５）　　Ａ　　（ｔ０＋）
例４　利用冲激函数匹配法求例四中的全响应
解　前面已推得系统的微分方程为：
ｄ２
ｄｔ２
ｉ（ｔ）＋７ｄｄｔｉ（ｔ）＋１０ｉ（ｔ）＝
ｄ２
ｄｔ２
ｅ（ｔ）＋６ｄｄｔｅ（ｔ）＋４ｅ（ｔ）
考虑到激励信号在ｔ＝０时刻由２Ｖ跃变到４Ｖ，代入上式即得ｔ＝０时的微分方程如下：
ｄ２
ｄｔ２
ｉ（ｔ）＋７ｄｄｔｉ（ｔ）＋１０ｉ（ｔ）＝２δ′（ｔ）＋１２δ（ｔ）＋８Δｕ（ｔ）
换路前：ｉ（０－）＝
４
５Ａ　
ｄ
ｄｔｉ（０－）＝０Ａ　　／ｓ
观察微分方程两侧可知：
ｄ２
ｄｔ２
ｉ（ｔ）项中包含δ′（ｔ）
因此可设：
（０－＜ｔ＜０＋）　
ｄ２
ｄｔ２
ｉ（ｔ）＝ａδ′（ｔ）＋ｂδ（ｔ）＋ｃΔｕ（ｔ）
ｄ
ｄｔｉ（ｔ）＝ａδ（ｔ）＋ｂΔｕ（ｔ）
ｉ（ｔ）＝ａΔｕ（ｔ







）
代入前式：
［ａδ′（ｔ）＋ｂδ（ｔ）＋ｃΔｕ（ｔ）］＋７［ａδ（ｔ）＋ｂΔｕ（ｔ）］＋１０ａΔｕ（ｔ）＝２δ′（ｔ）＋１２δ（ｔ）＋８Δｕ（ｔ）
比较系数：
ａ＝２
ｂ＋７ａ＝１２
ｃ＋７ｂ＋１０ａ＝
{
８
→　 　
ｉ（０＋）－ｉ（０－）＝ａ＝２
ｄ
ｄｔｉ（０＋）－
ｄ
ｄｔｉ（０－）＝ｂ＝－２
ｄ２
ｄｔ２
ｉ（０＋）－
ｄ２
ｄｔ２
ｉ（０－）＝ｃ＝







→
２
　
ｉ（０＋）＝ｉ（０－）＋２＝（
４
５＋２）＝
１４
５Ａ
ｄ
ｄｔｉ（０＋）＝
ｄ
ｄｔｉ（０－）－２＝－２
{ Ａ／ｓ
—６１—
三、零输入响应和零状态响应
例１　已知图示的ＲＣ电路，电容两端有起始电压ｖＣ（０－）试求时的电容ｔ＞０两端电压ｖＣ（ｔ）。
解：可求得系统方程为：
ｄ
ｄｔｖＣ（ｔ）＋
１
ＲＣｖＣ（ｔ）＝
１
ＲＣｅ（ｔ →）
［
ｄ
ｄｔｖＣ（ｔ）＋
１
ＲＣｖＣ（ｔ）］·ｅ
ｔ
ＲＣ ＝ １ＲＣｅ（ｔ）·ｅ
ｔ
→ＲＣ
ｄ
ｄｔ［ｅ
ｔ
ＲＣ·ｖＣ（ｔ）］＝
１
ＲＣｅ
ｔ
ＲＣ·ｅ（ｔ →）
∫
ｔ
０－
ｄ
ｄｔ［ｅ
τ
ＲＣ·ｖＣ（τ）］ｄτ＝∫
ｔ
０－
１
ＲＣｅ
τ
ＲＣ·ｅ（τ）ｄ →τ
ｅ
ｔ
ＲＣ·ｖＣ（ｔ）－ｖＣ（０－）＝
１
ＲＣ∫
ｔ
０－
ｅ
τ
ＲＣ·ｅ（τ）ｄ →τ
ｖＣ（ｔ）＝ｅ
－ｔＲＣ·ｖＣ（０－）＋
１
ＲＣ∫
ｔ
０－
ｅ－
１
ＲＣ（ｔ－τ）ｅ（τ）ｄτ
ｅ－
ｔ
ＲＣ·ｖＣ（０－）零输入响应ｒｚｉ（ｔ）
１
ＲＣ∫
ｔ
０－
ｅ－
１
ＲＣ（ｔ－τ）ｅ（τ）ｄτ零状态响应ｒｚｓ（ｔ）
零输入响应满足：
Ｃ０
ｄｎ
ｄｔｎ
ｒｚｉ（ｔ）＋Ｃ１
ｄｎ－１
ｄｔｎ－１
ｒｚｉ（ｔ）＋… ＋Ｃｎ－１
ｄ
ｄｔｒｚｉ（ｔ）＋Ｃｎｒｚｉ（ｔ）＝０
齐次解的一部分：ｒｚｉ（ｔ）＝∑
ｎ
ｋ＝１
Ａｚｉｋｅαｋ
ｔ
零状态响应满足：
Ｃ０
ｄｎ
ｄｔｎ
ｒｚｓ（ｔ）＋Ｃ１
ｄｎ－１
ｄｔｎ－１
ｒｚｓ（ｔ）＋… ＋Ｃｎ－１
ｄ
ｄｔｒｚｓ（ｔ）＋Ｃｎｒｚｓ（ｔ）
＝Ｅ０
ｄｍ
ｄｔｍ
ｅ（ｔ）＋Ｅ１
ｄｍ－１
ｄｔｍ－１
ｅ（ｔ）＋… ＋Ｅｍ－１
ｄ
ｄｔｅ（ｔ）＋Ｅｍｅ（ｔ）
初始状态：ｒ（ｋ）（０－）＝０　　（ｋ＝０，１，２，…ｎ－１）
其解：ｒｚｓ（ｔ）＝∑
ｎ
ｋ＝１
Ａｚｓｋｅαｋ
ｔ＋Ｂ（ｔ）
系统全响应：ｒ（ｔ）＝∑
ｎ
ｋ＝１
Ａｋｅαｋ
ｔ＋Ｂ（ｔ）＝∑
ｎ
ｋ＝１
Ａｚｉｋｅαｋ
ｔ＋∑
ｎ
ｋ＝１
Ａｚｓｋｅαｋ
ｔ＋Ｂ（ｔ）
例２　将图中ｔ＜０电路看做起始状态，分别求ｔ＞０时的零输入响应和零状态响应。
—７１—
郑君里《信号与系统》考点精讲
解：转换初始储能
前已求得：ｉＬ（０－）＝
４
５Ａ　ｖＣ（０－）＝
６
５Ｖ
ｄ２
ｄｔ２
ｉ（ｔ）＋７ｄｄｔｉ（ｔ）＋１０ｉ（ｔ）＝
ｄ２
ｄｔ２
ｅ（ｔ）＋６ｄｄｔｅ（ｔ）＋４ｅ（ｔ）
（图见视频）
１）零输入响应
→系统方程
ｄ２
ｄｔ２
ｉｉ（ｔ）＋７
ｄ
ｄｔｉｚｉ（ｔ）＋１０ｉｉ（ｔ）＝０
→初始状态 ｉｚｉ（０＋）
ｄ
ｄｔｉｚｉ（０＋）
（图见视频）
初始值等效电路ＫＣＬ、ＫＶＬ：
ｉｚｉ（０＋）＝－
ｖＣ（０＋）
Ｒ１
＝－
ｖＣ（０－）
Ｒ１
＝－６５Ａ
ｉＣ（０＋）＝ｉｚｉ（０＋）－ｉＬ（０＋）＝ｉｚｉ（０＋）－ｉＬ（０－）＝Ｃ
ｄ
ｄｔ［－Ｒ１·ｉｚｉ（０＋）］ｖＣ（０＋）
ｄ
ｄｔｉｚｉ（０＋）＝－
１
Ｒ１Ｃ
［ｉｚｉ（０＋）－ｉＬ（０＋）］＝２　　Ａ／ｓ
→零输入响应
ｄ２
ｄｔ２
ｉｉ（ｔ）＋７
ｄ
ｄｔｉｚｉ（ｔ）＋１０ｉｉ（ｔ）＝０
ｉｚｉ（０＋）＝－
６
５Ａ
ｄ
ｄｔｉｚｉ（０＋）＝２






 Ａ／ｓ
→ｉｚｉ（ｔ）＝（－
４
３ｅ
－２ｔ＋２１５ｅ
－５ｔ）　　Ａ　　（ｔ＞０）
２）零状态响应
（图见视频）
ｄ２
ｄｔ２
ｉｚｓ（ｔ）＋７
ｄ
ｄｔｉｚｓ（ｔ）＋１０ｉｚｓ（ｔ）＝
ｄ２
ｄｔ２
ｅ（ｔ）＋６ｄｄｔｅ（ｔ）＋４ｅ（ｔ）
已求得其全响应为：
—８１—
ｉｚｓ（ｔ）＝Ｃｚｓ１ｅ
－２ｔ＋Ｃｚｓ２ｅ
－５ｔ＋８５　　（ｔ＞０）
将ｅ（ｔ）＝４ｕ（ｔ）代入方程右端得自由项：ｄ
２
ｄｔ２
ｅ（ｔ）＋６ｄｄｔｅ（ｔ）＋４ｅ（ｔ）＝４δ′（ｔ）＋２４δ（ｔ）＋１６
根据冲激函数匹配法确定待定系数：
设：
ｄ２
ｄｔ２
ｉｚｓ（ｔ）＝ａδ′（ｔ）＋ｂδ（ｔ）＋ｃΔｕ（ｔ）
ｄ
ｄｔｉｚｓ（ｔ）＝ａδ（ｔ）＋ｂΔｕ（ｔ）
ｉｚｓ（ｔ）＝ａΔｕ（ｔ







）
　　（０－＜ｔ＜０＋）
代入微分方程，比较系数后整理可得：
ｉｚｓ（０＋）－ｉｚｓ（０－）＝ａ＝４
ｄ
ｄｔｉｚｓ（０＋）－
ｄ
ｄｔｉｚｓ（０－）＝ｂ＝－
{ ４
ｉｚｓ（０＋）＝４＋ｉｚｓ（０－）＝４
ｄ
ｄｔｉｚｓ（０＋）＝－４＋
ｄ
ｄｔｉｚｓ（０－）＝－
{ ４
ｉｚｓ（ｔ）＝Ｃｚｓ１ｅ
－２ｔ＋Ｃｚｓ２ｅ
－５ｔ＋８５　　（ｔ＞０







→
）
Ｃｚｓ１ ＝
８
３　　Ｃｚｓ１ ＝－
４
１５
系统零状态响应：
ｉｚｓ（ｔ）＝（
８
３ｅ
－２ｔ－４１５ｅ
－５ｔ＋８５）Ａ （ｔ＞０）
ｉ（ｔ）＝４３ｅ
－２ｔ－２１５ｅ
－５
     
ｔ
自由响应
暂态响应
＋　 ８５{　
强迫响应
稳态响应
＝（－４３ｅ
－２ｔ＋２１５ｅ
－５ｔ
       
）
令输入响应
＋（８３ｅ
－２ｔ－４１５ｅ
－５ｔ＋８５
         
）
零状态响应
四、冲激响应和阶跃响应
阶跃响应：单位阶跃信号作用下的零状态响应
冲激响应：单位冲激信号作用下的零状态响应
（图见视频）
对于ＬＴＩ系统，单位冲激响应满足：
Ｃ０ｈ
（ｎ）（ｔ）＋Ｃ１ｈ
（ｎ－１）（ｔ）＋… ＋Ｃｎ－１ｈ′（ｔ）＋Ｃｎｈ（ｔ）
＝Ｅ０δ
（ｍ）（ｔ）＋Ｅ１δ
（ｍ－１）（ｔ）＋… ＋Ｅｍ－１δ′（ｔ）＋Ｅｍδ（ｔ）
—９１—
郑君里《信号与系统》考点精讲
ｈ（ｋ）（０－）＝０
δ（ｔ）及其各阶导数ｔ０＋时恒为０，故：
Ｃ０ｈ
（ｎ）（ｔ）＋Ｃ１ｈ
（ｎ－１）（ｔ）＋… ＋Ｃｎ－１ｈ′（ｔ）＋Ｃｎｈ（ｔ）＝０
ｎ＞ｍ时：ｈ（ｔ）＝（∑
ｎ
ｋ＝１
Ｃｋｅαｋ
ｔ）ｕ（ｔ）
ｎ
"
ｍ时：采用冲激匹配法确定系数。
例３　求例２中电流ｉ（ｔ）的冲激响应ｈ（ｔ）和单位阶跃响应ｇ（ｔ）。
解：１）单位冲激响应
已求得系统方程为
ｄ２
ｄｔ２
ｉ（ｔ）＋７ｄｄｔｉ（ｔ）＋１０ｉ（ｔ）＝
ｄ２
ｄｔ２
ｅ（ｔ）＋６ｄｄｔｅ（ｔ）＋４ｅ（ｔ）
故其单位冲激响应满足：
ｈ″（ｔ）＋７ｈ′（ｔ）＋１０ｈ（ｔ）＝δ″（ｔ）＋６δ′（ｔ）＋４δ（ｔ）
其解为：
ｈ（ｔ）＝Ｃ１ｅ
－２ｔ＋Ｃ２ｅ
－５ｔ　　（ｔ０＋）
观察方程右侧，可设：
ｄ２
ｄｔ２
ｈ（ｔ）＝ａδ″（ｔ）＋ｂδ′（ｔ）＋ｃδ（ｔ）＋ｄΔｕ（ｔ）
ｄ
ｄｔｈ（ｔ）＝ａδ′（ｔ）＋ｂδ（ｔ）＋ｃΔｕ（ｔ）
ｈ（ｔ）＝ａδ（ｔ）＋ｂΔｕ（ｔ







）
　　（０－＜ｔ＜０＋）
代入方程解得：ａ＝１，ｂ＝－１，ｃ＝１故：
ｈ（０＋）＝ｂ＋ｈ（０－）＝－１
ｈ′（０＋）＝ｃ＋ｈ′（０－）＝
{ １
代入ｈ（ｔ）中解得：Ｃ１ ＝－
４
３　　Ｃ２ ＝
１
３
由于ｎ
"
ｍ，故ｈ（ｔ）中含有ａδ（ｔ）项因此：
ｈ（ｔ）＝δ（ｔ）＋（－４３ｅ
－２ｔ＋１３ｅ
－５ｔ）ｕ（ｔ）
２）单位阶跃响应
ｇ″（ｔ）＋７ｇ′（ｔ）＋１０ｇ（ｔ）＝δ′（ｔ）＋６δ（ｔ）＋４ｕ（ｔ）
ｇ′（０－）＝ｇ（０－）＝０
全响应为：ｇ（ｔ）＝Ｃ１ｅ
－２ｔ＋Ｃ２ｅ
－５ｔ＋Ｂ　　（ｔ０＋）
根据特解形式得：
１０Ｂ＝４
—０２—
特解：ｇｐ（ｔ）＝
２
５
根据冲激函数匹配法设：
ｄ２
ｄｔ２
ｇ（ｔ）＝ａδ′（ｔ）＋ｂδ（ｔ）＋ｃΔｕ（ｔ）
ｄ
ｄｔｈ（ｔ）＝ａδ（ｔ）＋ｂΔｕ（ｔ）
ｇ（ｔ）＝ａΔｕ（ｔ







）
　　（０－＜ｔ＜０＋）
代入方程解得：ａ＝１，ｂ＝－１，ｃ＝１故：
ｇ（０＋）＝ａ＋ｇ（０－）＝１
ｇ′（０＋）＝ｂ＋ｇ′（０－）＝－
{ →
１
Ｃ１ ＝２／３
Ｃ２ ＝－１／
{ １５
全响应：ｇ（ｔ）＝（２３ｅ
－２ｔ－１１５ｅ
－５ｔ＋２５）ｕ（ｔ）
五、卷积
原理：将信号进行冲击分解，根据系统ｈ（ｔ）求任意激励信号的零状态响应
ｆ１（ｔ）ｆ２（ｔ）∫
!
－
!
ｆ１（τ）ｆ２（ｔ－τ）ｄτ＝ｆ２（ｔ）ｆ１（ｔ）
则系统的零状态响应为：ｒ（ｔ）＝ｅ（ｔ）ｈ（ｔ）＝∫
!
－
!
ｅ１（τ）ｈ（ｔ－τ）ｄτ
计算：
１）转换自变量
２）反折
３）平移
４）相乘
５）积分
例１　计算图示信号的卷积
（图见视频）
１）－
!
＜ｔ
"
－０．５时
—１２—
郑君里《信号与系统》考点精讲
ｅ（ｔ）ｈ（ｔ）＝０
２）－０．５
"
ｔ
"
１且ｔ－２
"
－０．５时
ｅ（ｔ）ｈ（ｔ）＝∫
ｔ
－０．５
１×１２（ｔ－τ）ｄτ＝
ｔ２
４＋
ｔ
４＋
１
１６
３）ｔ１且ｔ－２"－０．５时，１"ｔ"３２
ｅ（ｔ）ｈ（ｔ）＝∫
１
－０．５
１×１２（ｔ－τ）ｄτ＝
３ｔ
４＋
３
１６
４）－１２"
ｔ－２
"
１且ｔ１时，３２"
ｔ
"
３
ｅ（ｔ）ｈ（ｔ）＝∫
１
ｔ－２
１×１２（ｔ－τ）ｄτ＝－
ｔ２
４＋
ｔ
２＋
３
４
５）ｔ－２１且ｔ１时，ｅ（ｔ）ｈ（ｔ）＝０
综上可得ｅ（ｔ）ｈ（ｔ）如下图所示：
六、卷积的性质
熟练掌握卷积各种性质的数学证明
１．卷积代数
１）交换律
２）分配律
３）结合律
ｆ１（ｔ）ｆ２（ｔ）＝ｆ２（ｔ）ｆ１（ｔ）
ｆ１（ｔ）［ｆ２（ｔ）＋ｆ３（ｔ）］＝ｆ１（ｔ）ｆ２（ｔ）＋ｆ１（ｔ）ｆ３（ｔ）
［ｆ１（ｔ）ｆ２（ｔ）］ｆ３（ｔ）＝ｆ１（ｔ）［ｆ２（ｔ）ｆ３（ｔ）］
系统串并联
（图见视频）
２）卷积的微分与积分特性
ｄ
ｄｔ［ｆ１（ｔ）ｆ２（ｔ）］＝ｆ１（ｔ）
ｄ
ｄｔｆ２（ｔ）＝ｆ２（ｔ）
ｄ
ｄｔｆ１（ｔ）
∫
ｔ
－
!
［ｆ１（λ）ｆ２（λ）］ｄλ＝ｆ１（ｔ）∫
ｔ
－
!
ｆ２（λ）ｄλ＝ｆ２（ｔ）∫
ｔ
－
!
ｆ１（λ）ｄλ
设：ｓ（ｔ）＝ｆ１（ｔ）ｆ２（ｔ）
—２２—
则：ｓ（ｉ）（ｔ）＝ｆ（ｊ）１ （ｔ）ｆ
（ｉ－ｊ）
２ （ｔ）
３）与冲激函数或阶跃函数的卷积
ｆ（ｔ）δ（ｔ）＝∫
!
－
!
ｆ（τ）δ（ｔ－τ）ｄτ
ｆ（ｔ）δ（ｔ）＝∫
!
－
!
ｆ（τ）δ（ｔ－τ）ｄτ
筛选性 ＝∫
!
－
!
ｆ（τ）δ（τ－ｔ）ｄτ＝ｆ（ｔ）
信号与单位冲激信号的卷积为本身
ｆ（ｔ）δ（ｔ－ｔ０）＝∫
!
－
!
ｆ（τ）δ（ｔ－ｔ０－τ）ｄτ＝ｆ（ｔ－ｔ０）
结论：与δ（ｔ－ｔ０）卷积的结果是延迟个时间单位。
利用卷积的微分、积分特性可得：
ｆ（ｔ）δ′（ｔ）＝ｆ′（ｔ）
ｆ（ｔ）ｕ（ｔ）＝∫
ｔ
－
!
ｆ（τ）ｄτ
一般形式：
ｆ（ｔ）δ（ｋ）（ｔ）＝ｆ（ｋ）（ｔ）
ｆ（ｔ）δ（ｋ）（ｔ－ｔ）＝ｆ（ｋ）（ｔ－ｔ０）
例２　利用卷积特性重新计算计算例１中的卷积
解：根据微分、积分特性得
ｒ（ｔ）＝ｅ（ｔ）ｈ（ｔ）＝ｄｄｔｅ（ｔ）∫
ｔ
－
!
ｈ（τ）ｄτ
∫
ｔ
－
!
ｈ（τ）ｄτ＝∫
ｔ
－
!
１
２τ［ｕ（τ）－ｕ（τ－２）］ｄτ
＝（∫
ｔ
－
!
１
２τｄτ）ｕ（ｔ）－（∫
ｔ
－
!
１
２τｄτ）ｕ（ｔ－２）
＝１４ｔ
２［ｕ（ｔ）－ｕ（ｔ－２）］＋ｕ（ｔ－２）＝ｈ（－１）（ｔ）
ｄ
ｄｔｅ（ｔ）＝δ（ｔ＋
１
２）－δ（ｔ－１）
ｒ（ｔ）＝ｅ（ｔ）ｈ（ｔ）＝ｄｄｔｅ（ｔ）∫
ｔ
－
!
ｈ（τ）ｄτ
＝ １
４（ｔ＋
１
２）
２
［ｕ（ｔ＋１２）－ｕ（ｔ－
３
２）］＋ｕ（ｔ－
３
２{ }）－ １
４（ｔ－１）
２［ｕ（ｔ－１）－ｕ（ｔ－３）］＋ｕ（ｔ－３{ }）
—３２—
郑君里《信号与系统》考点精讲
＝
０．２５（ｔ＋０．５）２　　 －０．５
"
ｔ＜１
０．７５（ｔ－０．２５）　　１
"
ｔ＜１．５
１－０．２５（ｔ－１）２　　１．５
"
ｔ＜
{
３
可得：
七、微分方程的算子解法
基本算子：ｐ＝ｄｄｔ　　
１
ｐ＝∫
ｔ
－
!
（…）ｄτ
系统的微分方程可用算子法描述为：
（Ｃ０ｐ
ｎ＋Ｃ１ｐ
ｎ－１＋… ＋Ｃｎ－１ｐ＋Ｃｎ）ｒ（ｔ）＝（Ｅ０ｐ
ｍ ＋Ｅ１ｐ
ｍ－１＋… ＋Ｅｍ－１ｐ＋Ｅｍ）ｅ（ｔ）
１．基本规则
１）算子公因子不能对消
２）算子乘除顺序不能颠倒
先“乘”后“除”不抵消
ｐ１ｐｘ≠
１
ｐｐｘ
先“除”后“乘”可抵消
２．算立法简历微分方程
ｖＬ（ｔ）＝Ｌ
ｄ
ｄｔｉＬ（ｔ）＝Ｌｐ·ｉＬ（ｔ）　等效电感
ｖＣ（ｔ）＝
１
Ｃ∫
ｔ
－
!
ｉＣ（τ）ｄτ＝
１
Ｃｐ·ｉＣ（ｔ）　等效电容
例３　利用算子法建立系统方程。
解：用算子符号表示电路元件
—４２—
（图见视频）
根据ＫＶＬ：
（Ｒ１＋
１
Ｃｐ）ｉ（ｔ）－
１
ＣｐｉＬ（ｔ）＝ｅ（ｔ）
－１Ｃｐｉ（ｔ）＋
１
Ｃｐ（Ｌｐ＋Ｒ２＋
１
Ｃｐ）ｉＬ（ｔ）＝
{ ０
应用克莱姆法则解得：
ｉ（ｔ）＝
（
１
Ｒ１
ｐ＋
Ｒ２
Ｒ１Ｌ
＋ １
Ｒ１ＬＣｐ
）
ｐ＋（
Ｒ２
Ｌ＋
１
Ｒ１Ｃ
）＋（１ＬＣ＋
Ｒ２
Ｒ１ＬＣ
）
１
ｐ
允许先积分后微分，同乘ｐ得：
ｉ（ｔ）＝
（
１
Ｒ１
ｐ２＋
Ｒ２
Ｒ１Ｌ
ｐ＋ １
Ｒ１ＬＣ
）
ｐ２＋（
Ｒ２
Ｌ＋
１
Ｒ１Ｃ
）ｐ＋（１ＬＣ＋
Ｒ２
Ｒ１ＬＣ
）
·ｅ（ｔ）
代入参数整理后得：
ｄ２
ｄｔ２
ｉ（ｔ）＋７ｄｄｔｉ（ｔ）＋１０ｉ（ｔ）＝
ｄ２
ｄｔ２
ｅ（ｔ）＋６ｄｄｔｅ（ｔ）＋４ｅ（ｔ）
八、小结
１．ＬＴＩ连续系统的响应：
全响应＝齐次解（自由响应）＋特解（强迫响应）
２．关于０－和０＋初始值
当系统已经用微分方程表示时，如果包含有
#
（ｔ）及其各阶导数，说明相应的０－状态到０＋状态
发生了跳变。冲激函数匹配法。
３．零输入响应和零状态响应
ｙ（ｔ）＝ｙｈ（ｔ）＋ｙｐ（ｔ）
自由响应＋强迫响应；暂态响应＋稳态响应；
零输入响应＋零状态响应
４．冲激响应和阶跃响应
５．卷积积分
定义，计算的５个过程
６．卷积积分的性质
交换律、分配率、结合律
利用性质求卷积
—５２—
郑君里《信号与系统》考点精讲
第三章　傅立叶变换
一、引言
通过本章的学习掌握以下内容：
１．周期信号和非周期信号频谱分析的方法
———傅立叶级数和傅立叶变换
２．周期信号和非周期信号频谱的特点与区别
３．理解非周期信号频谱密度函数的概念
４．信号时域特性与频域特性之间的关系
５．采样定理
要点：典型信号的傅立叶变换，利用傅立叶变换的
性质求信号的正、反变换，信号的频谱分析。
二、周期信号的傅立叶级数分析
１．三角函数形式的傅里叶级数
（１）狄利克雷条件
在一周期内，如果有间断点存在，则间断点的数目应该是有限个；
在一周期内，极大值和极小值的数目应该是有限个；
在一周期内，信号是绝对可积的。
周期信号可以由一系列不同角频率的三角函数的线性组合来逼近：
（２）描述
ｆ（ｔ）＝ａ０＋ａ１ｃｏｓ（ω１ｔ）＋ｂ１ｓｉｎ（ω１ｔ）＋ａ２ｃｏｓ（２ω１ｔ）＋ｂ２ｓｉｎ（２ω１ｔ）＋…＋ａｎｃｏｓ（ｎω１ｔ）＋ｂｎｓｉｎ（ｎω１ｔ）＋…
＝ａ０＋∑
!
ｎ＝１
［ａｎｃｏｓ（ｎω１ｔ）＋ｂｎｓｉｎ（ｎω１ｔ）］
—６２—
ａ０ ＝
１
Ｔ１∫
ｔ０＋Ｔ１
ｔ０
ｆ（ｔ）ｄｔ—直流分量幅值
ａｎ ＝
２
Ｔ１∫
ｔ０＋Ｔ１
ｔ０
ｆ（ｔ）ｃｏｓ（ｎω１ｔ）ｄｔ—余弦分量幅值
ｂｎ ＝
２
Ｔ１∫
ｔ０＋Ｔ１
ｔ０
ｆ（ｔ）ｓｉｎ（ｎω１ｔ）ｄｔ———正弦分量幅值
合并、整理可得：
ｆ（ｔ）＝ｃ０＋∑
!
ｎ＝１
ｃｎｃｏｓ（ｎω１ｔ＋φｎ）
其系数如下：
ａ０ ＝ｃ０，ｃｎ ＝ ａ２ｎ＋ｂ
２
槡 ｎ，φｎ ＝－ａｒｃｔａｎ
ｂｎ
ａｎ
ｓｉｎφｎ ＝
－ｂｎ
ａ２ｎ＋ｂ
２
槡 ｎ
，ｃｏｓφｎ ＝
ａｎ
ａ２ｎ＋ｂ
２
槡 ｎ
ａｎ ＝ｃｎｃｏｓφｎ，ｂｎ ＝－ｃｎｓｉｎφ







ｎ
直流分量、基波、二次谐波、三次谐波……
２．复指数形式的傅里叶级数
欧拉公式：
ｃｏｓｎω０ ＝
１
２（ｅ
ｊｎω０＋ｅ－ｊｎω０）
ｓｉｎｎω０ ＝
１
ｊ２（ｅ
ｊｎω０＋ｅ－ｊｎω０ }
）
ｏｒ　ｅ±ｊｎω０ ＝ｃｏｓｎω０±ｊｓｉｎｎω０
代入三角函数形式的傅立叶级数可得：
ｆ（ｔ）＝ｃ０＋∑
!
ｎ＝１
ｃｎｃｏｓ（ｎω０ｔ＋φｎ）
＝ｃ０＋∑
!
ｎ＝１
ｃｎ
２［ｅ
ｊ（ｎω０ｔ＋φｎ）＋ｅ－ｊ（ｎω０ｔ＋φｎ）］
＝ｃ０＋∑
!
ｎ＝１
ｃｎ
２ｅ
ｊｎω０ｔｅｊφｎ＋∑
!
ｎ＝１
ｃｎ
２ｅ
－ｊｎω０ｔｅ－ｊφｎ
＝ｃ０＋∑
!
ｎ＝１
ｃｎ
２ｅ
ｊｎω０ｔｅｊφｎ＋∑
－
!
ｎ＝－１
ｃ－ｎ
２ｅ
－ｊｎω０ｔｅ－ｊφ－ｎ
＝ｃ０＋∑
!
ｎ＝１
ｃｎ
２ｅ
ｊｎω０ｔｅｊφｎ＋∑
－１
ｎ＝－
!
ｃｎ
２ｅ
ｊｎω０ｔｅｊφｎ
整理后可得复指数形式的傅立叶级数：
ｆ（ｔ）＝∑
!
ｎ＝－
!
ｃｎ
２ｅ
ｊｎω１ｔｅｊφｎ ＝∑
!
ｎ＝－
!
Ｆ（ｎω０）ｅ
ｊｎω１ｔａ＝∑
!
ｎ＝－
!
Ｆｎｅ
ｊｎω１ｔ
—７２—
郑君里《信号与系统》考点精讲
其中：Ｆｎ ＝Ｆ（ｎω１）＝
１
Ｔ∫
ｔ０＋Ｔ
ｔ０
ｆ（ｔ）ｅ－ｊｎω１ｔｄｔ
比较上述两种形式的傅立叶级数，可得到二者系数之间的关系：
Ｆ０ ＝ａ０ ＝ｃ０
Ｆｎ ＝ Ｆｎ ｅ
ｊφｎ ＝１２（ａｎ＋ｊｂｎ）＝
１
２ｃｎｅ
ｊφｎ
Ｆ－ｎ ＝
１
２（ａｎ＋ｊｂｎ）＝
１
２ｃｎｅ
－ｊφｎ
Ｆｎ ＝
１
２ｃｎ ＝ Ｆ－ｎ
φｎ ＝－ａｒｃｔａｎ
ｂｎ
ａｎ
Ｆｎ＋Ｆ－ｎ ＝２Ｒｅ［Ｆｎ］＝ａｎ
ｊ（Ｆｎ－Ｆ－ｎ）＝ｊ２Ｉｍ［Ｆｎ］＝ｂ

















ｎ
三角函数形式：ｃｎ ～ω，φｎ ～ω　　单边频谱
复指数的形式：Ｆｎ ～ω，φｎ ～ω　双边频谱
二者之间关系：Ｆ（ｎω１） ＝
１
２ｃｎ（ｎ≠０），Ｆ０ ＝ｃ０ ＝ａ０
幅值谱偶对称：Ｆ（ｎω１） ＝ Ｆ（－ｎω１）
相位谱奇对称：φ（ｎω１）＝－φ（－ｎω１）
３．周期信号的频谱及其特点
幅值、相角与角频率之间的关系分别称为幅值谱、相位谱，统称频率特性或频谱。
Ｆ（ｎω１）＝ Ｆ（ｎω１）ｅ
ｊφｎ
幅频特性：Ｆ（ｎω１） ＝
１
２ ａ２ｎ＋ｂ
２
槡 ｎ ＝
１
２ｃｎ
相频特性：φｎ ＝ａｒｃｔａｎ（
－ｂｎ
ａｎ
）
离散性、谐波性、收敛性引入负频率，无物理意义
例１　试做出信号：ｆ（ｔ）＝１＋ｓｉｎω１ｔ＋２ｃｏｓω１ｔ＋ｃｏｓ（２ω１ｔ＋
π
４）的两种形式的频谱。
解：整理原式得：ｆ（ｔ）＝１＋槡５ｃｏｓ（ω１ｔ－０．１５π）＋ｃｏｓ（２ω１ｔ＋
π
４）
ｃ０ ＝１　　ｃ１ ＝槡５＝２．２３６　　ｃ２ ＝１
φ０ ＝０　　φ１ ＝－０．１５π　　φ２ ＝０．２５π
—８２—
考试点（ｗｗｗ．ｋａｏｓｈｉｄｉａｎ．ｃｏｍ）名师精品课程　电话：４００－６８８５－３６５
利用欧拉公示化简得：
ｆ（ｔ）＝１＋（１．１２ｅ－ｊ０．１５πｅｊω１ｔ＋１．１２ｅｊ０．１５πｅ－ｊω１ｔ）＋（０．５ｅｊ０．２５πｅｊ２ω１ｔ＋０．５ｅ－ｊ０．２５πｅ－ｊ２ω１ｔ）
＝∑
２
ｎ＝－２
Ｆ（ｎω１）ｅ
ｊｎω１ｔ
４．函数的对称性与傅立叶系数的关系
当波形满足某种对称关系时，傅里叶级数中的某些特定项将不会出现，利用这种性质可以对谐波
成分迅速作出判断，以简化傅立叶系数的计算。常用的有：
周期对称：奇函数、偶函数
ｆ（ｔ）＝－ｆ（－ｔ）　　ｆ（ｔ）＝ｆ（－ｔ）
半周期对称：奇谐函数、偶谐函数
ｆ（ｔ）＝－ｆ（ｔ±Ｔ２）　　ｆ（ｔ）＝ｆ（ｔ±
Ｔ１
２）
（１）奇函数
ａｎ ＝０
ｂｎ ＝
４
Ｔ∫
Ｔ
２
０
ｆ（ｔ）ｓｉｎ（ｎω１ｔ）ｄｔ
Ｆｎ ＝－Ｆ－ｎ ＝－
１
２ｊｂｎ
φｎ ＝－
π
２
不含余弦项，只含有正弦项，傅立叶系数为虚数。
（２）偶函数
ａｎ ＝
４
Ｔ∫
Ｔ
２
０
ｆ（ｔ）ｃｏｓ（ｎω１ｔ）ｄｔ
ｂｎ ＝０
Ｆｎ ＝Ｆ－ｎ ＝
１
２ａｎ ＝
１
２ｃｎ
φｎ ＝０
不含正弦项，只含有余弦项和直流项，傅立叶系数为实函数。
（３）奇谐函数
ｎ为奇数时：
ａｎ ＝
４
Ｔ∫
Ｔ
２
０
ｆ（ｔ）ｃｏｓ（ｎω１ｔ）ｄｔ
ｂｎ ＝
４
Ｔ∫
Ｔ
２
０
ｆ（ｔ）ｓｉｎ（ｎω１ｔ）ｄｔ
—９２—
郑君里《信号与系统》考点精讲
（４）偶谐函数
ｎ为偶数时：
ａｎ ＝
４
Ｔ∫
Ｔ
２
０
ｆ（ｔ）ｃｏｓ（ｎω１ｔ）ｄｔ
ｂｎ ＝
４
Ｔ∫
Ｔ
２
０
ｆ（ｔ）ｓｉｎ（ｎω１ｔ）ｄｔ
５．傅里叶有限级数与最小方均误差，吉布斯现象
ｆ（ｔ）＝ａ０＋∑
!
ｎ＝１
［ａｎｃｏｓ（ｎω１ｔ）＋ｂｎｓｉｎ（ｎω１ｔ）］
ＳＮ ＝ａ０＋∑
Ｎ
ｎ＝１
［ａｎｃｏｓ（ｎω１ｔ）＋ｂｎｓｉｎ（ｎω１ｔ）］
εＮ（ｔ）＝ｆ（ｔ）－ＳＮ　　误差项
ＥＮ ＝εＮ
２（ｔ）＝１Ｔ１∫
ｔ０＋Ｔ１
ｔ０
εＮ
２（ｔ）ｄｔ
ＥＮ ＝εＮ
２（ｔ）＝ｆ２（ｔ）－［ａ０
２＋１２∑
Ｎ
ｎ＝１
（ａｎ
２＋ｂｎ
２）］
有限项逼近所产生的方均误差
由上式可知：ｌｉｍ
Ｎ→!
ＳＮ ＝ｆ（ｔ）
对于对称方波的逼近分析发现：
（１）Ｎ越大，越接近方波
（２）快变信号，高频分量，主要影响跳变沿；
（３）慢变信号，低频分量，主要影响顶部；
（４）任一分量的幅度或相位发生相对变化时，波形将会失真。
相数越多，合成波形中出现的峰起越靠近原函数的不连续点，其值约为总跳变量的９％。称为“吉
布斯现象”。
—０３—
三、典型周期信号的傅立叶级数
１．周期矩形脉冲信号
其在一个周期内的表达式为：
ｆ（ｔ）＝［ｕ（ｔ＋π２）－ｕ（ｔ－
π
２）］
偶函数，ｂｎ ＝０只有ａ０、ａｎ项。
Ｆ（ｎω１）＝
１
Ｔ１∫
Ｔ１
２
－
Ｔ１
２
ｆ（ｔ）ｅ－ｊｎω１ｔｄｔ
＝１Ｔ１∫
τ
２
－τ２
Ｅｅ－ｊｎω１ｔｄｔ＝ＥτＴ１
Ｓａ（ｎω１
τ
２）
求得：
ｆ（ｔ）＝ＥτＴ１＋
Ｅτω１
π ∑
!
ｎ＝１
Ｓａ（ｎω１τ２ ）ｃｏｓ（ｎω１ｔ）
ｆ（ｔ）＝ＥτＴ１∑
!
ｎ＝－
!
Ｓａ（ｎω１τ２ ）ｅ
ｊｎω１τ
Ｆ（ｎω１）为实数Ｆｎ ＞０，相位０，Ｆｎ ＜０，相位 ±π
当Ｔ１→ !
时，ω１→０，
Ｅτ
Ｔ１
为无限小，
ｆ（ｔ）由周期信号→非周期信号
信号能量的主要部分称为带宽，记为：
Ｂω ＝
２π
τ
或Ｂｆ＝
１
τ
—１３—
郑君里《信号与系统》考点精讲
当上述矩形信号为方波时，既是偶函数，又是奇谐函数，故只有基波和奇次余弦谐波分量
ｆ（ｔ）＝２Ｅ
π
［ｃｏｓ（ω１ｔ）－１３ｃｏｓ（３ω１ｔ）＋
１
５ｃｏｓ（５ω１ｔ）－…］
谐波幅值以１／ｎ收敛
由矩形脉冲信号的频谱特性印证了周期信号频谱的特点：离散性、谐波性、收敛性。
２．周期锯齿脉冲
ｆ（ｔ）＝Ｅ
π∑
!
ｎ＝１
（－１）ｎ＋１ １ｎｓｉｎ（ｎω１ｔ）
只包含正弦分量，谐波幅值以１／ｎ收敛
３．周期三角脉冲
ｆ（ｔ）＝Ｅ２＋
４Ｅ
π２∑
!
ｎ＝１
１
ｎ２
ｓｉｎ２（ｎπ２）ｃｏｓ（ｎω１ｔ）
包含直流分量、基波以及奇次谐波分量，谐波幅值以１／ｎ２收敛。
４．周期半波余弦信号
ｆ（ｔ）＝Ｅ
π
－２Ｅ
π∑
!
ｎ＝１
１
（ｎ２－１）
ｃｏｓ（ｎπ２）ｃｏｓ（ｎω１ｔ）
包含直流分量、基波以及各次谐波分量，
谐波幅值以１／ｎ２收敛。
四、傅立叶变换
１．由傅立叶级数到傅立叶变换
Ｔ１→ !
　　ｌｉｍ
Ｔ→!
ｆＴ（ｔ）＝ｆ（ｔ）
—２３—
Ｆ（ｎω１）＝
１
Ｔ１∫
Ｔ１
２
－
Ｔ１
２
ｆ（ｔ）ｅ－ｊｎω１ｔｄｔ→０
频谱间隔：ω１ ＝
２π
Ｔ１
→０
→离散谱 连续谱
谱系数Ｆｎ ＝Ｆ（ｎω１）无意义，但仍有相当对大小关系。
谱系数两侧同时乘以周期
Ｔ１Ｆ（ｎω１）＝
Ｆ（ｎω１）
１／Ｔ ＝
Ｆ（ｎω１）
ｆ 　　单位频带上的频谱
Ｔ１→ !
时，ｆ＝１Ｔ１
→０，Ｆ（ｎω１）→０
谱线间隔：Δ（ｎω１）＝ω１→ｄω（ｎω１）→ω
Ｆ（ω）＝ｌｉｍ
Ｔ１→!
Ｔ１Ｆ（ｎω１）＝ｌｉｍＴ１→!
∫
Ｔ１
２
－
Ｔ１
２
ｆ（ｔ）ｅ－ｊｎω１ｔｄｔ＝∫
!
－
!
ｆ（ｔ）ｅ－ｊｎωｔｄｔ　　频谱密度函数
称上式为信号的傅立叶变换
Ｆ（ω）＝｜Ｆ（ω）｜ｅｊφ（ω）
Ｆ（ω） ～ω：幅值谱
φ（ω）～ω：相位谱
２．傅立叶反变换
Ｆ（ｊω）＝∫
!
－
!
ｆ（ｔ）ｅ－ｊωｔｄｔ
ｆＴ（ｔ）＝∑
!
ｎ＝－
!
１
Ｔ［∫
Ｔ
２
－Ｔ２
ｆＴ（ｔ）ｅ
－ｊｎω１ｔｄｔ］ｅｊｎω１ｔ
ｆＴ（ｔ）＝∑
!
ｎ＝－
!
ω１
２π
［∫
Ｔ
２
－Ｔ２
ｆＴ（ｔ）ｅ
－ｊｎω１ｔｄｔ］ｅｊｎω１ｔ
ｆ（ｔ）＝∫
!
－
!
１
２π
（∫
!
－
!
ｆ（ｔ）ｅ－ｊωｔｄｔ）ｅｊωｔｄω
ｆ（ｔ）＝ １２π∫
!
－
!
Ｆ（ｊω）ｅｊωｔｄω
记：Ｆ（ω）＝∫
!
－
!
ｆ（ｔ）ｅ－ｊωｔｄｔ＝Ｆ［ｆ（ｔ）］
ｆ（ｔ）＝ １２π∫
!
－
!
Ｆ（ｊω）ｅｊωｔｄω＝Ｆ－１［Ｆ（ｊω）］
分别称为傅立叶变换和傅立叶反变换
３．傅立叶变换的物理意义
ｆ（ｔ）＝ １２π∫
!
－
!
Ｆ（ω）ｅｊωｔｄω
＝ １２π∫
!
－
!
Ｆ（ω）ｅｊφ（ω）ｅｊωｔｄω
—３３—
郑君里《信号与系统》考点精讲
＝ １２π∫
!
－
!
Ｆ（ω）ｃｏｓ［ωｔ＋φ（ω）］ｄω＋ｊ
１
２π∫
!
－
!
Ｆ（ω）ｓｉｎ［ωｔ＋φ（ω）］ｄω
＝１
π∫
!
０
Ｆ（ω）ｃｏｓ［ωｔ＋φ（ω）］ｄω
＝∫
!
０
Ｆ（ω）
π
ｄωｃｏｓ［ωｔ＋φ（ω）］
ｆ（ｔ）＝∫
!
０
Ｆ（ω）
π
ｄωｃｏｓ［ωｔ＋φ（ω）］
求和　　幅值　　余弦信号
无穷多个振幅为（
１
π Ｆ（ω）
ｄω）余弦信号之和
ｆ（ｔ）＝ １２π∫
!
－
!
Ｆ（ω）ｅｊωｔｄω＝∫
!
－
!
Ｆ（ω）
２π
ｄω·ｅｊωｔ
求和　　幅值　　复指数信号
无穷多个振幅为（
１
２π Ｆ（ω）
ｄω）复指数信号之和
４．傅立叶变换存在的条件
信号绝对可积∫
!
－
!
ｆ（ｔ）ｄｔ＜!
所有能量信号均满足此条件。
充分非必要条件。借助奇异函数的概念，许多不满足此条件的信号都存在傅立叶变换。
五、典型非周期信号的傅立叶变换
１．单边指数信号
ｆ（ｔ）＝
ｅ－αｔｔ＞０α＞０
０ｔ＜{ ０
Ｆ（ω）＝Ｆ［ｆ（ｔ）］＝∫
!
－
!
ｅ－αｔｕ（ｔ）ｅ－ｊωｔｄｔ＝∫
!
０
ｅ－（α＋ｊω）ｔｄｔ＝ １
α＋ｊω
　　
Ｆ（ω） ＝
１
α２＋ω槡
２
ω＝０，Ｆ（ω） ＝
Ｅ
α
ω→±!
，Ｆ（ω）→
{
０
　　
φ（ω）＝－ａｒｃｔａｎωα
ω→０，φ（ω）＝０
ω→＋!
，φ（ω）→－π２
ω→－!
，φ（ω）→ π







２
　　
—４３—
２．双边指数信号
ｆ（ｔ）＝ｅ－ａ｜ｔ｜（－
!
＜ｔ＜＋
!
）　　ａ＞０
Ｆ（ω）＝∫
!
－
!
ｆ（ｔ）ｅ－ｊωｔｄｔ＝∫
!
０
ｅ－（ａ＋ｊω）ｔｄｔ
　　　
Ｆ（ω）＝ １
ａ－ｊω
＋ １
ａ＋ｊω
＝ ２ａ
ａ２＋ω２
Ｆ（ω）＝ ２ａ
ａ２＋ω２
＝ Ｆ（ω）
φ（ω）＝
}
０
　　　
３．矩形脉冲信号
ｆ（ｔ）＝Ｅ［ｕ（ｔ＋τ２）－ｕ（ｔ－
τ
２）］
Ｆ（ω）＝∫
τ
２
－τ２
Ｅｅ－ｊωｔｄｔ＝ＥτＳａ（ωτ２）
Ｆ（ω） ＝ＥτＳａ（ωτ２）
φ（ω）＝
０　（４ｎπ
τ
＜ ω ＜
２（２ｎ＋１）π
τ
）
π　（２（２ｎ＋１）πτ
＜ ω ＜
４（ｎ＋１）π
τ
{
）
４．钟形脉冲信号（高斯信号）
ｆ（ｔ）＝Ｅｅ－（
ｔ
τ）２（－
!
＜ｔ＜＋
!
）
Ｆ（ω）＝槡πＥτｅ
－（ωτ２）２
５．符号函数
ｆ（ｔ）＝ｓｇｎ（ｔ）＝
＋１，ｔ＞０
－１，ｔ＜{ ０
—５３—
郑君里《信号与系统》考点精讲
处理方法：
衰减因子
ｆ１（ｔ）＝ｓｇｎ（ｔ）ｅ
－α ｔ
求Ｆ１（ω），求极限得到Ｆ（ω）
Ｆ１（ω）＝∫
０
－
!
－ｅαｔｅ－ｊωｔｄｔ＋∫
!
０
ｅ－αｔｅ－ｊωｔｄｔ
＝ －１
α－ｊω
＋ １
α＋ｊω
＝ －ｊ２ω
α２＋ω２
Ｆ（ω）＝ｌｉｍ
α→０
Ｆ１（ω）＝ｌｉｍ
α→０
－ｊ２ω
α２＋ω２
＝２ｊω
ｓｇｎ（ｔ） ２ｊω
＝－ｊ２
ω
＝ ２
ω
ｅｊ
π
２
Ｆ（ω） ＝（ （
２
ω
）
槡
２
＝ ２
ω
）
Ｆ（ω）是偶函数
ａｒｃｔａｎ
－２
ω
０ ＝
－π２，ω＞０
π
２，ω＜
{ ０
φ（ω）是奇函数
６．升余弦脉冲信号
ｆ（ｔ）＝Ｅ２［１＋ｃｏｓ（
πｔ
τ
）］０
" ｔ"τ
Ｆ（ω）＝∫
!
－
!
ｆ（ｔ）ｅ－ｊωｔｄｔ
＝∫
τ
－τ
Ｅ
２［１＋ｃｏｓ（
πｔ
τ
）］ｅ－ｊωｔｄｔ
＝Ｅ２∫
τ
－τ
ｅ－ｊωｔｄｔ＋Ｅ４∫
τ
－τ
ｅｊ
πｔ
τｅ－ｊωｔｄｔ＋Ｅ４∫
τ
－τ
ｅ－ｊ
πｔ
τｅ－ｊωｔｄｔ
＝ＥτＳａ（ωτ）＋Ｅτ２Ｓａ［（ω－
π
τ
）τ］＋Ｅτ２Ｓａ［（ω＋
π
τ
）τ］
（图见视频）
六、冲激函数和阶跃函数的傅立叶变换
１．冲击函数的傅立叶变换
Ｆ（ω）＝∫
!
－
!
δ（ｔ）ｅ－ｊωｔｄｔ
—６３—
２．冲激偶函数的傅立叶变换
∫
!
－
!
ｆ（ｔ）δ′（ｔ）ｄｔ＝－ｆ′（０）
Ｆ［δ′（ｔ）］＝∫
!
－
!
δ′（ｔ）ｅ－ｊωｔｄｔ＝－［ｅ－ｊωｔ］′ｔ＝０ ＝－（－ｊω）＝ｊω
３．阶跃函数的傅立叶变换
ｕ（ｔ）＝１２＋
１
２ｓｇｎ（ｔ）
１
２πδ（ω）
１
２ｓｇｎ（ｔ）
１
ｊω
ｕ（ｔ）πδ（ω）＋１ｊω
—７３—
郑君里《信号与系统》考点精讲
七、傅立叶变换的基本性质
对称性、线性（叠加性）、奇偶虚实性、尺度变换特性、时移特性、频移特性、微分特性、积分特性。
重点掌握在基本的傅里叶变换对基础上利用上述八个性质对一般信号进行付傅立叶变换的方
法，了解傅里叶变换在通讯系统领域中的应用。
δ（ｔ）１
ｕ（ｔ） １ｊω
＋πδ（ω）
ｕ（ｔ）ｅ－αｔ １
α＋ｊω
ｅｊω０ｔ２πδ（ω－ω０）
ｅ－ａｔ２ π
槡ａ
ｅ－
ω２
４ａ
１．对称性
若：ｆ（ｔ）Ｆ（ω），则：Ｆ（ｔ）２πｆ（－ω）
特殊的：ｆ（ｔ）为偶函数时，Ｆ（ｔ）２πｆ（ω）
利用已知变换对方便的求出信号的傅里叶变换。
（图见视频）
２．线性（叠加性和齐次性）
若：ｆ１（ｔ）Ｆ１（ω），ｆ２（ｔ）Ｆ２（ω）
则：ｃ１ｆ１（ｔ）＋ｃ２ｆ２（ｔ）ｃ１Ｆ１（ω）＋ｃ２Ｆ２（ω）
傅里叶正、反变换公式为求积分（求和）复杂信号分解后求和。
３．奇偶虚实性
Ｆ（ω）＝∫
!
－
!
ｆ（ｔ）ｅ－ｊωｔｄｔ
＝∫
!
－
!
ｆ（ｔ）ｃｏｓωｔｄｔ－ｊ∫
!
－
!
ｆ（ｔ）ｓｉｎωｔｄｔ
＝Ｒ（ω）＋ｊＸ（ω）＝Ｆ（ω）＝ Ｆ（ω）ｅ－ｊφ（ω）
其中：
Ｒ（ω）＝∫
!
－
!
ｆ（ｔ）ｃｏｓωｔｄｔ＝Ｒ（－ω）
Ｘ（ω）＝－ｊ∫
!
－
!
ｆ（ｔ）ｓｉｎωｔｄｔ＝－Ｘ（－ω）
Ｆ（ω） ＝ Ｒ２（ω）＋Ｘ２（ω槡 ）
φ（ω）＝ａｒｃｔａｎＸ（ω）Ｒ（ω）
＝－φ（－ω











）
为ω的偶函数
为ω的奇函数
为ω的偶函数
为ω的奇函数
结论：
—８３—
ｆ（－ｔ）Ｆ（－ω）
ｆ（ｔ）Ｆ（－ω）
ｆ（ｔ）为实函数时，ｆ（－ｔ）Ｆ（－ω）＝Ｆ（ω）
４．尺度变换
若：ｆ（ｔ）Ｆ（ω）
则：ｆ（ａｔ） １
ａＦ（
ω
ａ），ａ≠０
意义：
→时域压缩 频域扩展
→时域扩展 频域压缩
→时域对折 频域对折
信号的等效脉冲宽度与其等效带宽成反比（图见视频）
５．时移特性
若ｆ（ｔ）Ｆ（ω），则ｆ（ｔ－ｔ０）Ｆ（ω）ｅ
－ｊωｔ０；
设Ｆ（ω）＝ Ｆ（ω）ｅｊφ（ω），则ｆ（ｔ－ｔ０） Ｆ（ω）·ｅｊ［φ（ω）－ωｔ０］
不影响幅度频谱，只影响相位频谱
６．频移特性
若ｆ（ｔ）Ｆ（ω）则ｆ（ｔ）ｅ±ｊω０ｔＦ（ωω０）
通信中调制与解调，频分复用。
时域ｆ（ｔ）乘以ｅｊω０ｔ，频谱右移ω０
时域ｆ（ｔ）乘以ｅ－ｊω０ｔ，频谱左移ω０
７．微分特性
若：ｆ（ｔ）Ｆ（ω）
则：
ｄ（ｎ）ｆ（ｔ）
ｄｔｎ
（ｊω）ｎＦ（ω）　时域微分
ｄ（ｎ）Ｆ（ω）
ｄωｎ
（－ｊｔ）ｎｆ（ｔ）　{
频域微分
应用：ｕ（ｔ） １ｊω
＋πδ（ω）　　δ（ｔ）１　　δ′（ｔ）Ｆ（ω）
８．积分特性
若：ｆ（ｔ）Ｆ（ω）
则：∫
ｔ
－
!
ｆ（τ）ｄτＦ（ω）ｊω
＋πＦ（０）δ（ω）
例１　求图示信号的频谱
—９３—
郑君里《信号与系统》考点精讲
解：已知矩形信号的频谱为采样信号，即
ｆ０（ｔ）Ｆ０（ω）＝ＥτＳａ（
ωτ
２）
（图见视频）
而三脉冲矩形信号可表示为：
ｆ（ｔ）＝ｆ０（ｔ）＋ｆ０（ｔ＋Ｔ）＋ｆ０（ｔ－Ｔ）
根据傅里叶变换的线性特性和时移特性：
Ｆ（ω）＝Ｆ０（ω）（１＋ｅ
ｊωＴ＋ｅ－ｊωＴ）＝Ｅτ·Ｓａ（ωτ２）［１＋２ｃｏｓ（ωＴ）］
（图见视频）
与矩形信号相比：
脉冲数目增多时，幅频特性包络线不变，带宽不变。
例２　试求双Ｓａ信号的频谱。
解：由例１和傅里叶变换的对称性知：采样信号
ｆ０（ｔ）＝
ωｃ
π
Ｓａ（ωｃｔ）的频谱为矩形。如图：
Ｆ［ｆ０（ｔ）］＝
１（ω ＜ωｃ）
０（ω ＜ωｃ
{
）
根据傅里叶变换的时移特性知：
Ｆ［ｆ０（ｔ－２τ）］＝
ｅ－ｊ２ωｔ（ω ＜ωｃ）
０（ω ＜ωｃ
{
）
根据傅里叶变换的线性特性得双Ｓａ信号的频谱：
Ｆ（ω）＝Ｆ［ｆ０（ｔ）］－Ｆ［ｆ０（ｔ－２τ）］＝
１－ｅ－ｊ２ωτ（ω ＜ωｃ）
０（ω ＜ωｃ
{
）
其幅频特性为：
Ｆ（ω） ＝
２ｓｉｎ（ωτ）（ω ＜ωｃ）
０（ω ＜ωｃ
{
）
—０４—
由于实际中常取τ＝πωｃ
故：
Ｆ（ω） ＝
２ｓｉｎ（πω
ωｃ
）（ω ＜ωｃ）
０（ω ＜ωｃ
{
）
因此，双Ｓａ信号及其频谱如下：
与单Ｓａ信号相比，没有直流分量，便于传输。
例３　设矩形脉冲信号Ｇ（ｔ）的高度为Ｅ，宽度为τ，试求矩形调幅信号ｆ（ｔ）＝Ｇ（ｔ）ｃｏｓ（ω０ｔ），的频谱。
解：Ｇ（ω）＝Ｅτ·Ｓａ（ωτ２）　ｆ（ｔ）＝
１
２Ｇ（ｔ）（ｅ
ｊω０ｔ＋ｅ－ｊω０ｔ）
根据傅里叶变换的频移特性得原信号的频谱为：
（图见视频）
Ｆ（ω）＝１２Ｇ（ω－ω０）＋
１
２Ｇ（ω＋ω０）＝
Ｅτ
２Ｓａ［
（ω－ω０）τ
２ ］＋Ｅτ２Ｓａ［
（ω＋ω０）τ
２ ］
例４　ｆ（ｔ）＝
Ｅ（１－２
τ ｔ
）（ｔ＜τ２）
０（ｔ＞τ２
{
）
，求三角脉冲信号的频谱
解：取原信号的一阶及二阶导数得：
（图见视频）
ｄｆ（ｔ）
ｄｔ ＝
２
τ
Ｅ（－τ２ ＜ｔ＜０）
－２
τ
Ｅ（０＜ｔ＜τ２）
０（ｔ＞τ２







）
ｄ２ｆ（ｔ）
ｄｔ２
＝２Ｅ
τ
［δ（ｔ＋τ２）＋δ（ｔ－
τ
２）－２δ（ｔ）］
二者的时域波形如下图：
—１４—
郑君里《信号与系统》考点精讲
根据傅里叶变换的微分特性可得：
Ｆ［ｆ″（ｔ）］＝∫
!
－
!
［
２Ｅ
τδ
（ｔ＋τ２）－
４Ｅ
τδ
（ｔ）＋２Ｅ
τδ
（ｔ－τ２）］ｅ
－ｊωｔｄｔ
＝２Ｅ
τ
ｅｊω
τ
２ －４Ｅ
τ
＋２Ｅ
τ
ｅ－ｊω
τ
２ ＝（ｊω）２Ｆ（ω）＝－ω２Ｆ（ω）
整理可得：
Ｆ（ω）＝ １
－ω２
［
２Ｅ
τ
ｅｊω
τ
２ －４Ｅ
τ
＋２Ｅ
τ
ｅ－ｊω
τ
２］
＝ １
－ω２
２Ｅ
τ
［ｅｊω
τ
２ －２＋ｅ－ｊω
τ
２］
＝－２Ｅ
τω２
［ｅｊω
τ
４ －ｅ－ｊω
τ
４］２ ＝－２Ｅ
τω２
（２ｊｓｉｎωτ４）
２
＝８Ｅ
τω２
（ｓｉｎωτ４）
２（
ωτ
４）
２
（
ωτ
４）
２ ＝
τＥ
２Ｓａ（
ωτ
４）
２
（图见视频）
例５　求图示信号的傅里叶变换
解：（图见视频）
根据傅里叶变换的积分特性：
Ｆ２（ω）＝［πδ（ω）＋
１
ｊω
］Ｓａ（ω２）ｅ
－ｊω２ ＝πδ（ω）＋
Ｓａ（ω２）ｅ
－ｊω２
ｊω
Ｆ（ω）＝Ｆ［１］＋Ｆ２（ω）＝３πδ（ω）＋
Ｓａ（ω２）ｅ
－ｊω２
ｊω
９．卷积特性
１）时域卷积定理
若：ｆ１（ｔ）Ｆ１（ω），ｆ２（ｔ）Ｆ２（ω）
则：ｆ１（ｔ）ｆ２（ｔ）Ｆ１（ω）·Ｆ２（ω）
Ｆ［ｆ１（ｔ）ｆ２（ｔ）］＝∫
!
－
!
［∫
!
－
!
ｆ１（τ）ｆ２（ｔ－τ）ｄτ］ｅ
－ｊωｔｄｔ
＝∫
!
－
!
ｆ１（τ）［∫
!
－
!
ｆ２（ｔ－τ）ｅ
－ｊωｔｄｔ］ｄτ
＝∫
!
－
!
ｆ１（τ）Ｆ２（ω）ｅ
－ｊωｔｄｔ
—２４—
＝Ｆ１（ω）Ｆ２（ω）
２）频域卷积定理
若：ｆ１（ｔ）Ｆ１（ω），ｆ２（ｔ）Ｆ２（ω）
则：ｆ１（ｔ）·ｆ２（ｔ）
１
２π
Ｆ１（ω）Ｆ２（ω）
卷积定理揭示了时域运算与频域运算的对应关系：
时域乘积对应频域卷积，时域卷积对应频域乘积。
系统的变换域分析法的基础。
例６　求下述余弦脉冲信号的频谱。
ｆ（ｔ）＝
Ｅｃｏｓ（πｔ
τ
）（ｔ"τ２）
０（ｔ＞τ２
{
）
解：（图见视频）
将余弦信号用窗函数截取，即可得到
余弦脉冲信号：ｆ（ｔ）＝Ｇ（ｔ）ｃｏｓ（πｔ
τ
）
Ｆ（ω）＝Ｆ［Ｇ（ｔ）·ｃｏｓ（πｔτ
）］
＝ １２π
·［ＥτＳａ（ωτ２）］［πδ（ω＋
π
τ
）＋πδ（ω－πτ
）］
＝Ｅτ２Ｓａ［（ω＋
π
τ
）
τ
２］＋
Ｅτ
２Ｓａ［（ω－
π
τ
）
τ
２］
考点：掌握各种基本信号的傅里叶变换对，灵活运用傅里叶变换的各种特性对一般信号进行频谱
分析。
八、周期信号的傅立叶变换
满足狄利克雷条件的周期信号
ｆｐ（ｔ）→傅里叶级数Ｆ（ｎω１）离散谱
满足绝对可积条件的非周期信号
ｆ（ｔ）→傅里叶变换Ｆ（ω）连续谱
一般的周期信号是否可进行傅里叶变换？
ｆｐ（ｔ）→ ∑
!
ｎ＝－
!
Ｆｎｅ
ｊｎω１ｔ或ｃ０＋∑
!
ｎ＝－
!
ｃｎｃｏｓ（ｎω１ｔ＋φｎ）
存在傅里叶变换
单位冲击信号的引入，使绝对可积成为非必要条件，
一般的周期信号存在ＦＴ。
—３４—
郑君里《信号与系统》考点精讲
１．正、余弦信号的傅立叶变换
已知１２πδ（ω）根据频移特性可得：
１·ｅｊω１ｔ２πδ（ω－ω１）
１·ｅ－ｊω１ｔ２πδ（ω＋ω１）
应用欧拉公式，根据线性特性可得：
ｃｏｓω１ｔ
１
２［２πδ（ω－ω１）＋２πδ（ω＋ω１）］
＝πδ（ω＋ω１）＋πδ（ω－ω１）
ｓｉｎω１ｔ
１
２ｊ［２πδ（ω－ω１）－２πδ（ω＋ω１）］
＝ｊπδ（ω＋ω１）－ｊπδ（ω－ω１）
根据上节例３，对矩形脉冲信号求极限，并根据单位冲击信号的采样信号定义：δ（ｔ）＝ｌｉｍ
ｋ→!
ｋ
π
Ｓａ（ｋｔ）
（图见视频）
２．一般周期信号的傅立叶变换
ＦＴ（ω）＝Ｆ［ｆＴ（ｔ）］
＝Ｆ［∑
!
－
!
Ｆ（ｎω１）ｅ
ｊｎω１ｔ］
＝∑
!
－
!
Ｆ（ｎω１）Ｆ［ｅ
ｊｎω１ｔ］
＝２π∑
!
－
!
Ｆ（ｎω１）δ（ω－ｎω１）
其中：Ｆ（ｎω１）＝
１
Ｔ∫
Ｔ１
２
－
Ｔ１
２
ｆ（ｔ）ｅ－ｊｎω１ｔｄｔ
从上式中可以看出：周期信号的傅里叶变换是由一系列位于信号谐波频率的冲击函数组成的，冲
击信号的幅值等于原信号傅里叶级数相应系数的２π倍。
例１　求图示周期信号的傅里叶变换
解：
Ｆｎ ＝
１
Ｔ∫Ｔｆ（ｔ）·ｅ－ｊω１ｔｄｔ
＝１２∫
３
２
－１２
［Ｇ１
２
（ｔ）－Ｇ１
２
（ｔ－１）］ｅ－ｊｎπｔｄｔ
—４４—
＝
ｓｉｎｎπ４
ｎπ
［１－（－１）ｎ］
Ｆ（ω）＝Ｆ［ｆ（ｔ）］
＝２π∑
!
ｎ＝－
!
Ｆｎδ（ω－ｎπ）
＝２∑
!
ｎ＝－
!
ｓｉｎｎπ４
ｎ ［１－（－１）ｎ］δ（ω－ｎπ）
３．单脉冲信号的频谱密度与周期信号谱系数的关系
设单个脉冲信号ｆ０（ｔ）周期拓展后得到：ｆＴ（ｔ）
ｆ０（ｔ）＝
１
２π∫
!
－
!
Ｆ０（ω）ｅ
ｊωｔｄω
Ｆ０（ω）＝∫
!
－
!
ｆ０（ｔ）ｅ
－ｊωｔ{ ｄｔ
　　　　
ｆＴ（ｔ）＝∑
!
ｎ＝－
!
Ｆ（ｎω１）ｅ
ｊｎω１ｔ
Ｆ（ｎω１）＝
１
Ｔ１∫
Ｔ
２
－Ｔ２
ｆＴ（ｔ）ｅ
－ｊｎω１ｔ{ ｄｔ
（图见视频）
比较后可得二者关系：Ｆ（ｎω１）＝
１
Ｔ１
Ｆ０（ω）
ω＝ｎω１
例２　求周期单位冲激序列的傅里叶变换
δＴ（ｔ）＝∑
!
ｎ＝－
!
δ（ｔ－ｎＴ１）δ（ｔ）１
可得δＴ（ｔ）的傅里叶级数谱系数
Ｆ（ｎω１）＝
１
Ｔ１
Ｆ０（ω）
ω＝ｎω１
＝１Ｔ１
δＴ（ｔ）＝∑
!
ｎ＝－
!
Ｆ（ｎω１）ｅ
ｊｎω１ｔ＝１Ｔ１∑
!
ｎ＝－
!
ｅｊｎω１ｔ
Ｆ（ω）＝Ｆ［δＴ（ｔ）］
＝１Ｔ１∑
!
ｎ＝－
!
Ｆ［ｅｊｎω１ｔ］
＝１Ｔ１∑
!
ｎ＝－
!
２πδ（ω－ｎω１）
＝ω１∑
!
ｎ＝－
!
δ（ω－ｎω１）＝δω（ω）
＝２πＴ１∑
!
ｎ＝－
!
δ（ω－ｎω１）
（图见视频）
—５４—
郑君里《信号与系统》考点精讲
例３　求周期矩形脉冲序列的傅里叶变换。
Ｆ０（ω）→Ｆ（ｎω１）→Ｆ（ω）
Ｆ０（ω）＝ＥτＳａ（
ωτ
２）
Ｆ（ｎω１）＝
１
Ｔ１
Ｆ０（ω）
ω＝ｎω１
Ｆ（ω）＝２π∑
!
ｎ＝－
!
Ｆ（ｎω１）·δ（ω－ｎω１）
＝２π∑
!
ｎ＝－
!
Ｅτ
Ｔ１
Ｓａ（
ｎω１τ
２ ）δ（ω－ｎω１）
＝Ｅτω１∑
!
ｎ＝－
!
Ｓａ（
ｎω１τ
２ ）δ（ω－ｎω１）
（图见视频）
在定义了单位冲激信号之后，周期信号的傅里叶级数和傅里叶变换得到了统一，掌握由傅里叶级
数的系数求傅里叶变换的方法。
九、抽样信号的傅立叶变换
（图见视频）
１．时域抽样
周期抽样脉冲的频谱：Ｐ（ω）＝２π∑
!
ｎ＝－
!
Ｐｎδ（ω－ｎωｓ）
其中：Ｐｎ ＝
１
Ｔｓ∫
Ｔｓ
２
－
Ｔｓ
２
ｐ（ｔ）ｅ－ｊωｓｔｄｔ
设采样器模型为：ｆｓ（ｔ）＝ｆ（ｔ）ｐ（ｔ）
根据频域卷积定理得：
Ｆｓ（ω）＝２πＦ（ω）Ｐ（ω）＝∑
!
ｎ＝－
!
ＰｎＦ（ω－ｎωｓ）
可见，采样之后所的信号的频谱是原始信号频谱的加权和，权系数为采样脉冲的傅里叶系数。
１）矩形脉冲抽样（自然抽样）
Ｐｎ ＝
１
Ｔｓ∫
Ｔｓ
２
－
Ｔｓ
２
ｐ（ｔ）ｅ－ｊｎωｓｔｄｔ＝１Ｔｓ∫
Ｔｓ
２
－
Ｔｓ
２
Ｅｅ－ｊｎωｓｔｄｔ＝ＥτＴｓ
Ｓａ（
ｎωｓτ
２ ）
—６４—
Ｆｓ（ω）＝
Ｅτ
Ｔｓ∑
!
ｎ＝－
!
Ｓａ（
ｎωｓτ
２ ）Ｆ（ω－ｎωｓ）
将原始信号的频谱按照采样信号的规律重复。
自然抽样的频谱关系
（图见视频）
２）冲激抽样（理想抽样）
ｐ（ｔ）＝δＴ（ｔ）＝∑
!
ｎ＝－
!
δ（ｔ－ｎＴｓ）ωｓ∑
!
－
!
δ（ω－ｎωｓ）
ｆｓ（ｔ）＝ｆ（ｔ）δＴ（ｔ）＝∑
!
ｎ＝－
!
ｆ（ｎＴｓ）δ（ｔ－ｎＴｓ）
Ｆｓ（ω）＝Ｆ［ｆ（ｔ）δＴ（ｔ）］＝
１
２π
Ｆ（ω）δＴ（ω）＝
１
Ｔｓ∑
!
ｎ＝－
!
Ｆ（ω－ｎωｓ）
将原始信号的频谱按照等幅的规律重复。
理想抽样的频谱关系
（图见视频）
２．频域抽样
对频域信号进行理想抽样，研究二者所对应的时域信号之间的关系。
Ｆ１（ω）＝Ｆ（ω）δω（ω）δω（ω）＝∑
!
ｎ＝－
!
δ（ω－ｎω１）
Ｆ［∑
!
ｎ＝－
!
δ（ｔ－ｎＴ１）］＝ω１∑
!
ｎ＝－
!
δ（ω－ｎω１）， （ω１＝２πＴ１）
Ｆ－１［∑
!
ｎ＝－
!
δ（ω－ｎω１）］＝１ω１∑
!
ｎ＝－
!
δ（ｔ－ｎＴ１）＝Ｆ－１［δω（ω）］＝
δＴ（ｔ）
ω１
ｆ１（ｔ）＝ｆ（ｔ）Ｆ－１［δω（ω）］＝
１
ω１∑
!
ｎ＝－
!
ｆ（ｔ－ｎＴ１）
频域理想抽样的时域对应关系（时域和频域离散的性与周期性相互对应关系）。
（图见视频）
十、抽样定理
１．时域抽样定理
—７４—
郑君里《信号与系统》考点精讲
从上图可知：ωｓ２ωｍ或ｆｓｆωｍ时，采样所得离散信号不发生频谱混叠。鉴于傅里叶变换一一
对应的关系，离散信号中保留了连续信号的所有特征，采样有效，可通过理想低通滤波器无失真的
恢复。
２．频域抽样定理
对于时间受限信号 ｔ"ｔｍ，对频域的采样间隔时，采样所得离散频谱所对应的时间信号不发生时
域混叠，采样有效，用窗函数从中选出单个脉冲即可无失真的恢复出原来的时域信号。
—８４—
２．名词定义
状态：对于一个动态系统的装态是表示系统的一组最小变量，只要知道ｔ＝ｔ０时这组变量和ｔｔ０
时的输入，那么就能完全确定系统在任何时间ｔｔ０的行为。
状态变量：能够表示系统状态的那些变量。
状态矢量：能够完全描述一个系统行为的ｋ个状态变量，可以看做矢量λ（ｔ）的各个分量的坐标。
状态空间：状态矢量λ（ｔ）所在的空间。
状态轨迹：在状态空间中，状态矢量端点随时间变化而推出的路径。
ｉＬ（ｔ）与ｕＣ（ｔ）与时间ｔ的关系
３．用状态变量分析系统的优点：
１）便于研究系统内部一些物理量在信号转换过程中的变化，这些物理量可以用状态矢量的一个
分量表现出来，从而便于研究其变化规律。
２）系统的状态分析法与系统的复杂程度没有关系，复杂系统和简单系统的数学模型形式相似，都
可表示为一些状态变量的线性组合。
３）状态方程的主要参数鲜明的表征了系统的关键性能，利用状态方程分析系统的稳定性也比较
方便。
４）状态变量分析法适用于非线性或时变系统。
５）由于状态方程都是一阶微分方程或一阶差分方程，因而便于采用数值解法，为使用计算机分析
系统提供了有效途径。
二、连续时间系统状态方程的建立
１．状态方程的一般形式和建立方法概述
一个动态连续系统的时域数学模型可利用信号的各阶导数来描述。作为连续系统的状态方程表
现为状态变量的一阶微分联立方程组，即：
状态方程
ｄ
ｄｔλ１（ｔ）＝ｆ１［λ１（ｔ），λ２（ｔ），…λｋ（ｔ）；ｅ１（ｔ），ｅ２（ｔ），…ｅｍ（ｔ），ｔ］
ｄ
ｄｔλ２（ｔ）＝ｆ２［λ１（ｔ），λ２（ｔ），…λｋ（ｔ）；ｅ１（ｔ），ｅ２（ｔ），…ｅｍ（ｔ），ｔ］
…
ｄ
ｄｔλｋ（ｔ）＝ｆｋ［λ１（ｔ），λ２（ｔ），…λｋ（ｔ）；ｅ１（ｔ），ｅ２（ｔ），…ｅｍ（ｔ），ｔ









］
—０８１—
输出方程
ｒ１（ｔ）＝ｈ１［λ１（ｔ），λ２（ｔ），…λｋ（ｔ）；ｅ１（ｔ），ｅ２（ｔ），Λｅｍ（ｔ），ｔ］
ｒ２（ｔ）＝ｈ２［λ１（ｔ），λ２（ｔ），…λｋ（ｔ）；ｅ１（ｔ），ｅ２（ｔ），Λｅｍ（ｔ），ｔ］
…
ｒｒ（ｔ）＝ｈｒ［λ１（ｔ），λ２（ｔ），…λｋ（ｔ）；ｅ１（ｔ），ｅ２（ｔ），Λｅｍ（ｔ），ｔ







］
对于线性时不变系统（ＬＴＩ），状态方程式状态变量和输入信号的线性组合，可用矢量矩阵形式表
示为：
用矢量矩阵形式可表示为：
状态方程
［
ｄ
ｄｔλ］ｋ×１
＝Ａｋ×ｋλｋ×１（ｔ）＋Ｂｋ×ｍｅｍ×１（ｔ）
输出方程
［ｒ（ｔ）］ｒ×１ ＝Ｃｒ×ｋλｋ×１（ｔ）＋Ｄｒ×ｍｅｍ×１（ｔ）
其中：
λ（ｔ）＝
λ１（ｔ）
λ２（ｔ）
…
λｋ（ｔ













）
Ａ＝
ａ１１ ａ１２ … ａ１ｋ
ａ２１ ａ２２ … ａ２ｋ
… … …
ａｋ１ ａｋ２ … ａ














ｋｋ
Ｃ＝
ｃ１１ ｃ１２ … ｃ１ｋ
ｃ２１ ｃ２２ … ｃ２ｋ
  
ｃｒ１ ｃｒ２ … ｃ














ｒｋ
ｄ
ｄｔλ（ｔ[ ]） ＝
ｄ
ｄｔλ１（ｔ）
ｄ
ｄｔλ２（ｔ）
…
ｄ
ｄｔλｋ（ｔ



















）
Ｂ＝
ｂ１１ ｂ１２ … ｂ１ｍ
ｂ２１ ｂ２２ … ｂ２ｍ
  
ｂｋ１ ｂｋ２ … ｂ














ｋｍ
Ｄ＝
ｄ１１ ｄ１２ … ｄ１ｍ
ｄ２１ ｄ２２ … ｄ２ｍ
  
ｄｒ１ ｄｒ２ … ｄ














ｒｍ
—１８１—
郑君里《信号与系统》考点精讲
ｒ（ｔ）＝
ｒ１（ｔ）
ｒ２（ｔ）
…
ｒｒ（ｔ













）
　　ｅ（ｔ）＝
ｅ（ｔ
ｅ（ｔ
…
ｅ（














ｔ
２．由电路图直接建立状态方程
状态变量（均为独立变量）：
电容两端电压与流经电感电流或电容电荷与电感磁链。
系统阶数（ｋ）：状态变量个数。
（图见视频）
注意选取独立变量
在选定状态变量之后，即可利用ＫＣＬ和ＫＶＬ列写电路方程，经化简消去一些不需要的变量，只留
下状态变量和输入信号经整理给出状态方程。
３．由系统的输入－输出方程或流图建立状态方程
假定某一物理系统可用如下微分方程表示
ｄｋ
ｄｔｋ
ｒ（ｔ）＋ａ１
ｄｋ－１
ｄｔｋ－１
ｒ（ｔ）＋… ＋ａｋ－１
ｄ
ｄｔｒ（ｔ）＋ａｋ
ｄｋ
ｄｔｋ
ｒ（ｔ）
＝ｂ０
ｄｋ
ｄｔｋ
ｅ（ｔ）＋ｂ１
ｄｋ－１
ｄｔｋ－１
ｅ（ｔ）＋… ＋ｂｋ－１
ｄ
ｄｔｅ（ｔ）＋ｂｋｅ（ｔ）
表示为算子形式为
（ｐｋ＋ａ１ｐ
ｋ－１＋Λ＋ａｋ－１ｐ＋ａｋ）ｒ（ｔ）＝（ｂ０ｐ
ｋ＋ｂ１ｐ
ｋ－１＋Λ＋ｂｋ－１ｐ＋ｂｋ）ｅ（ｔ）
为便于选择状态变量，将其传输算子表示成
Ｈ（ｐ）＝
ｂ０＋ｂ１／ｐ＋… ＋ｂｋ－１／ｐ
ｋ－１＋ｂｋ／ｐ
ｋ
１＋ａ１／ｐ＋… ＋ａｋ－１／ｐ
ｋ－１＋ａｋ／ｐ
ｋ
这样当用积分器来实现该系统时，有流图如下：
（图见视频）
将系统的状态方程和输出方程表示成矩阵简化形式：
λ
·
（ｔ）＝Ａλ（ｔ）＋Ｂｅ（ｔ）
ｒ（ｔ）＝Ｃλ（ｔ）＋Ｄｅ（ｔ{
）
对应的Ａ、Ｂ、Ｃ、Ｄ矩阵分别是：
—２８１—
Ａ＝
０ １ ０ …
０ ０ １ …
    
０ ０ ０ … １
－ａｋ －ａｋ－１ －ａｋ－２ … －ａ
















１
　　　Ｂ＝
０
０
０
















１
Ｃ＝［（ｂｋ－ａｋｂ０），（ｂｋ－１－ａｋ－１ｂ０），…（ｂ２－ａ２ｂ０），（ｂ１－ａ１ｂ０）］
Ｄ＝ｂ０
三、连续时间系统状态方程的求解
１．用拉普拉斯变换法求解状态方程
若给定方程：
ｄ
ｄｔλ（ｔ）＝Ａλ（ｔ）＋Ｂｅ（ｔ）
ｒ（ｔ）＝Ｃλ（ｔ）＋Ｄｅ（ｔ
{
）
两边取拉氏变换得
ｓΛ（ｓ）－λ（０－）＝ＡΛ（ｓ）＋ＢＥ（ｓ）
Ｒ（ｓ）＝ＣΛ（ｓ）＋ＤＥ（ｓ）
　　λ（０－）＝
λ１（０－）
λ２（０－）

λｋ（０－













）
式中：λ（０－）为初始条件
整理得
Λ（ｓ）＝（ｓＩ－Ａ）－１λ（０－）＋（ｓＩ－Ａ）
－１ＢＥ（ｓ）
Ｒ（ｓ）＝Ｃ（ｓＩ－Ａ）－１λ（０－）＋［Ｃ（ｓＩ－Ａ）
－１Ｂ＋Ｄ］Ｅ（ｓ{
）
因而时域表示式为：
λ（ｔ）＝Ｌ－１［（ｓＩ－Ａ）－１λ（０－）］＋Ｌ
－１［（ｓＩ－Ａ）－１Ｂ］Ｌ－１Ｅ（ｓ）
ｒ（ｔ）＝ＣＬ－１［（ｓＩ－Ａ）－１λ（０－）］＋｛ＣＬ
－１［（ｓＩ－Ａ）－１Ｂ］＋Ｄδ（ｔ）｝Ｌ－１Ｅ（ｓ
{
）
２．用时域法求解状态方程（矢量微分方程求解）
对给定的状态方程，若已知：
ｄ
ｄｔλ（ｔ）＝Ａλ（ｔ）＋Ｂｅ（ｔ）
并给定起始状态矢量λ（０－）＝
λ１（０－）
λ２（０－）

λｋ（０－













）
—３８１—
郑君里《信号与系统》考点精讲
可解得方程的一般解为
λ＝ｅＡｔλ（０－）＋ｅ
ＡｔＢｅ（ｔ）
将此结果带入输出方程得到
ｒ（ｔ）＝ＣｅＡｔλ（０－）＋［Ｃｅ
ＡｔＢ＋Ｄδ（ｔ）］ｅ（ｔ）
无论状态方程的解或输出方程的解都由零输入解（由λ（０－）引起）和零状态解（由ｅ（ｔ）引起）相
加组成。两部分的变化规律都与矩阵ｅＡｔ有关，因此ｅＡｔ反映了系统状态变化的本质。
ｅＡｔ称为“状态转移矩阵”，它的拉氏变化（ｓＩ－Ａ）－１称为“特征矩阵”。
其它直接求ｅＡｔ的方法：
１）计算机求解：将给定的Ａ带入ｅＡｔ＝∑
!
ｋ＝０
１
ｋ！Ａ
ｋｔｋ
利用计算机求无穷级数之和。
２）化对角阵计算法：若将Ａ矩阵化为对角阵 Ａ^，则ｅＡ^ｔ也是对角阵，当 Ａ^的对角各元素为ａｉ时，ｅ
Ａ^ｔ对
应元素为ｅａｉｔ，即：
Ａ^＝ｄｉａｇ［ａ１，ａ２，…，ａｋ］
ｅＡ^ｔ＝ｄｉａｇ［ｅａ１ｔ，ｅａ２ｔ，…，ｅａｋｔ］
３）化ｅＡｔ为有限项之和求解，此处需要利用凯莱 －哈密顿定理。
３．由状态方程求系统函数Ｈ（ｓ）
当给定系统的状态方程时，可利用已知的Ａ，Ｂ，Ｃ，Ｄ矩阵表示系统转移函数Ｈ（ｓ）。
设给定状态方程
λ（ｔ）＝Ａλ（ｔ）＋Ｂｅ（ｔ）
ｒ（ｔ）＝Ｃλ（ｔ）＋Ｄｅ（ｔ{
）
（Ａ，Ｂ，Ｃ，Ｄ为常数阵）
可得Ｈ（ｓ）＝Ｒ（ｓ）Ｅ（ｓ）＝Ｃ（ｓＩ－Ａ）
－１Ｂ＋Ｄ
对其取逆变换的冲击响应：ｈ（ｔ）＝ＣｅＡｔＢ＋Ｄδ（ｔ）
此外转移函数的一般表达式为：Ｈ（ｓ）＝
ｂ０ｓ
ｋ＋ｂ１ｓ
ｋ－１＋… ＋ｂｋ－１ｓ＋ｂｋ
ｓｋ＋ａ１ｓ
ｋ－１＋… ＋ａｋ－１ｓ＋ａｋ
比较上面转移函数表达式可以看出｜（ｓＩ－Ａ）｜即为Ｈ（ｓ）分的特征多项式，所以称（ｓＩ－Ａ）－１为
系统的特征矩阵。
四、离散时间系统状态方程的建立
１．状态方程的一般形式和建立方法概述
对于一个动态的时域离散系统，它的数学模型是用各阶差分方程形式描述的。作为离散系统的
状态方程表现为一阶差分联立方程组的形式。
即：
—４８１—
状态方程
λ１（ｎ＋１）＝ｆ１［λ１（ｎ），λ２（ｎ），…λｋ（ｎ）；ｘ１（ｎ），ｘ２（ｎ），…ｘｍ（ｎ），ｍ］
λ２（ｎ＋１）＝ｆ２［λ１（ｎ），λ２（ｎ），…λｋ（ｎ）；ｘ１（ｎ），ｘ２（ｎ），…ｘｍ（ｎ），ｍ］
…
λｋ（ｎ＋１）＝ｆｋ［λ１（ｎ），λ２（ｎ），…λｋ（ｎ）；ｘ１（ｎ），ｘ２（ｎ），…ｘｍ（ｎ），ｍ







］
输出方程
ｙ１（ｎ）＝ｈ１［λ１（ｎ），λ２（ｎ），…λｋ（ｎ）；ｘ１（ｎ），ｘ２（ｎ），…ｘｍ（ｎ），ｎ］
ｙ２（ｎ）＝ｈ２［λ１（ｎ），λ２（ｎ），…λｋ（ｎ）；ｘ１（ｎ），ｘ２（ｎ），…ｘｍ（ｎ），ｎ］
…
ｙｒ（ｎ）＝ｈｒ［λ１（ｎ），λ２（ｎ），…λｋ（ｎ）；ｘ１（ｎ），ｘ２（ｎ），…ｘｍ（ｎ），ｎ







］
如果是线性时不变系统，则状态方程和输出方程是状态变量和输入信号的线性组合，即：
状态方程
λ１（ｎ＋１）＝ａ１１λ１（ｎ）＋ａ１２λ２（ｎ）＋… ＋ａ１ｋλｋ（ｎ）＋ｂ１１ｘ１（ｎ）＋ｂ１２ｘ２（ｎ）＋… ＋ｂ１ｍｘｍ（ｎ）
λ２（ｎ＋１）＝ａ２１λ１（ｎ）＋ａ２２λ２（ｎ）＋… ＋ａ２ｋλｋ（ｎ）＋ｂ２１ｘ１（ｎ）＋ｂ２２ｘ２（ｎ）＋… ＋ｂ２ｍｘｍ（ｎ）
…
λｋ（ｎ＋１）＝ａｋ１λ１（ｎ）＋ａｋ２λ２（ｎ）＋… ＋ａｋｋλｋ（ｎ）
＋ｂｋ１ｘ１（ｎ）＋ｂｋ２ｘ２（ｎ）＋… ＋ｂｋｍｘｍ（ｎ









）
输出方程
ｙ１（ｎ）＝ｃ１１λ１（ｎ）＋ｃ１２λ２（ｎ）＋… ＋ｃ１ｋλｋ（ｎ）＋ｄ１１ｘ１（ｎ）＋ｄ１２ｘ２（ｎ）＋… ＋ｄ１ｍｘｍ（ｎ）
ｙ２（ｎ）＝ｃ２１λ１（ｎ）＋ｃ２２λ２（ｎ）＋… ＋ｃ２ｋλｋ（ｎ）
＋ｄ２１ｘ１（ｎ）＋ｄ２２ｘ２（ｎ）＋… ＋ｄ２ｍｘｍ（ｎ）
…
ｙｒ（ｎ）＝ｃｒ１λ１（ｎ）＋ｃｒ２λ２（ｎ）＋… ＋ｃｒｋλｋ（ｎ）＋ｄｒ１ｘ１（ｎ）＋ｄｒ２ｘ２（ｎ）＋… ＋ｄｒｍｘｍ（ｎ









）
２．由系统的输入 －输出差分方程建立状态方程
对于离散系统通常用下列ｋ阶差分方程描述
ｙ（ｎ）＋ａ１ｙ（ｎ－１）＋ａ２ｙ（ｎ－２）＋… ＋ａｋ－１ｙ［ｎ－（ｋ－１）］＋ａｋｙ（ｎ－ｋ）
＝ｂ０ｘ（ｎ）＋ｂ１ｘ（ｎ－１）＋ｂ２ｘ（ｎ－２）＋… ＋ｂｋ－１ｘ［ｎ－（ｋ－１）］＋ｂｋｘ（ｎ－ｋ）
表示成算子形式为
（Ｅｋ＋ａ１Ｅ
ｋ－１＋ａ２Ｅ
ｋ－２＋… ＋ａｋ－１Ｅ＋ａｋ）ｙ（ｎ）
＝（ｂ０Ｅ
ｋ＋ｂ１Ｅ
ｋ－１＋ｂ２Ｅ
ｋ－２＋…ｂｋ－１Ｅ＋ｂｋ）ｘ（ｎ）
传输算子为
Ｈ（Ｅ）＝
ｂ０＋ｂ１／Ｅ＋ｂ２／Ｅ
２＋… ＋ｂｋ－１／Ｅ
ｋ－１＋ｂｋ／Ｅ
ｋ
１＋ａ１／Ｅ＋ａ２／Ｅ
２＋… ＋ａｋ－１Ｅ
ｋ－１＋ａｋ／Ｅ
ｋ
—５８１—
郑君里《信号与系统》考点精讲
（图见视频）
如图，选延时单元作为状态变量，则有：
λ１（ｎ＋１）＝λ２（ｎ）
λ２（ｎ＋１）＝λ３（ｎ）

λｋ－１（ｎ＋１）＝λｋ（ｎ）
λｋ（ｎ＋１）＝－ａｋλ１（ｎ）－ａｋ－１λ２（ｎ）－…
－ａ２λｋ－１（ｎ）－ａ１λｋ（ｎ）＋ｘ（ｎ











）
ｙ（ｎ）＝（ｂｋ－ａｋｂ０）λ１（ｎ）＋（ｂｋ－１－ａｋ－１ｂ０）λ２（ｎ）＋… ＋（ｂ２－ａ２ｂ０）λｋ－１（ｎ）＋（ｂ１－ａ１ｂ０）λｋ（ｎ）
＋ｂ０ｘ（ｎ）
表示成矢量方程的形式为
λ（ｎ＋１）＝Ａλ（ｎ）＋Ｂｅ（ｎ）
ｙ（ｔ）＝Ｃλ（ｎ）＋Ｄｅ（ｎ{
）
其中
Ａ＝
０ １ ０ …
０ ０ １ …
    
０ ０ ０ … １
－ａｋ －ａｋ－１ －ａｋ－２ … －ａ
















１
　　Ｂ＝
０
０
０
















１
Ｃ＝［（ｂｋ－ａｋｂ０），（ｂｋ－１－ａｋ－１ｂ０），…（ｂ２－ａ２ｂ０），（ｂ１－ａ１ｂ０）］
Ｄ＝ｂ０
可见根据离散系统的传输算子来列写系统的状态方程其步骤和结果与连续系统是一样的。
３．由给定系统的方框图或流图建立状态方程
给定系统的方框图或流图，只要取延时单元的输出作为状态变量便可建立系统的状态方程。
作为状态方程与输出方程，在形式上是相同的，就是由输入量、输出量、状态变量以及联系它们之
间关系Ａ、Ｂ、Ｃ、Ｄ矩阵构成。
对连续系统状态方程和输出方程形式为
λ
·
（ｔ）＝Ａλ（ｔ）＋Ｂｅ（ｔ）
ｒ（ｔ）＝Ｃλ（ｔ）＋Ｄｅ（ｔ{
）
对离散系统状态方程和输出方程形式为
λ（ｎ＋１）＝Ａλ（ｎ）＋Ｂｅ（ｎ）
ｙ（ｔ）＝Ｃλ（ｎ）＋Ｄｅ（ｎ{
）
—６８１—
五、离散时间系统状态方程的求解
离散系统状态方程的求解和连续系统的求解方法相似，包括时域和变化域。
１．矢量差分方程的时域求解
离散系统的状态方程为在ｎ＝ｎ０有λ（ｎ０），则有
λ（ｎ０＋１）＝Ａλ（ｎ０）＋Ｂｅ（ｎ０）
当ｎ＞ｎ０利用迭代法可归结为：
λ（ｎ）＝Ａｎ－ｎ０λ（ｎ０）＋∑
ｎ－１
ｉ＝ｎ０
Ａｎ－１－ｉＢｘ（ｉ）
若ｎ０ ＝０，并将上述对ｎ值得限制以阶跃信号的形式写入表达式
λ（ｎ）＝Ａｎλ（０）ｕ（ｎ）＋［∑
ｎ－１
ｉ＝ｎ０
Ａｎ－１－ｉＢｘ（ｉ）］ｕ（ｎ－１）
解得输出为：
ｙ（ｎ）＝Ｃλ（ｎ）＋Ｄｘ（ｎ）＝ＣＡｎλ（０）ｕ（ｎ）＋［∑
ｎ－１
ｉ＝ｎ０
ＣＡｎ－１－ｉＢｘ（ｉ）］ｕ（ｎ－１）＋Ｄｘ（ｎ）ｕ（ｎ）
若令ｘ（ｎ）＝δ（ｎ），则系统的单位脉冲响应为
ｈ（ｎ）＝ＣＡｎ－１Ｂｕ（ｎ－１）＋Ｄδ（ｎ）
２、Ａｎ的计算
与连续系统的情况类似，离散系统状态方程时域求解的关键步骤是计算状态转移矩阵，即Ａｎ
利用凯莱 －哈密顿定理，有
Ａｊ＝ｃ０Ｉ＋ｃ１Ａ＋ｃ２Ａ
２＋… ＋ｃｋ－１Ａ
ｋ－１（ｊｋ）
分别用Ａ的特征值代入上式，解联立方程即可求出系数
ｃ０，ｃ１，Λ，ｃｋ－１
３．离散系统状态方程的ｚ变换解
由离散系统的状态方程和输出方程
λ（ｎ＋１）＝Ａλ（ｎ）＋Ｂｅ（ｎ）
ｙ（ｔ）＝Ｃλ（ｎ）＋Ｄｅ（ｎ{
）
两边取ｚ变换并整理得
Λ（ｚ）＝（ｚＩ－Ａ）－１ｚλ（０）＋（ｚＩ－Ａ）－１ＢＸ（ｚ）
Ｙ（ｚ）＝Ｃ（ｚＩ－Ａ）－１ｚλ（０）＋Ｃ（ｚＩ－Ａ）－１ＢＸ（ｚ）＋ＤＸ（ｚ{
）
取其逆变换即得时域表示式为
λ（ｎ）＝Ｚ－１［（ｚＩ－Ａ）－１ｚ］λ（０）＋Ｚ－１［（ｚＩ－Ａ）－１Ｂ］Ｚ－１［Ｘ（ｚ）］
ｙ（ｎ）＝Ｚ－１［Ｃ（ｚＩ－Ａ）－１］ｚλ（０）＋Ｚ－１［Ｃ（ｚＩ－Ａ）－１Ｂ＋Ｄ］Ｚ－１［Ｘ（ｚ{
）］
状态转移矩阵为
Ａｎ－１ｕ（ｎ－１）＝Ｚ－１［Ｃ（ｚＩ－Ａ）－１］
—７８１—
郑君里《信号与系统》考点精讲
两边取ｚ变换并整理得
Λ（ｚ）＝（ｚＩ－Ａ）－１ｚλ（０）＋（ｚＩ－Ａ）－１ＢＸ（ｚ）
Ｙ（ｚ）＝Ｃ（ｚＩ－Ａ）－１ｚλ（０）＋Ｃ（ｚＩ－Ａ）－１ＢＸ（ｚ）＋ＤＸ（ｚ{
）
取其逆变换即得时域表示式为
λ（ｎ）＝Ｚ－１［（ｚＩ－Ａ）－１ｚ］λ（０）＋Ｚ－１［（ｚＩ－Ａ）－１Ｂ］Ｚ－１［Ｘ（ｚ）］
ｙ（ｎ）＝Ｚ－１［Ｃ（ｚＩ－Ａ）－１］ｚλ（０）＋Ｚ－１［Ｃ（ｚＩ－Ａ）－１Ｂ＋Ｄ］Ｚ－１［Ｘ（ｚ{
）］
状态转移矩阵为
Ａｎ－１ｕ（ｎ－１）＝Ｚ－１［Ｃ（ｚＩ－Ａ）－１］
六、状态矢量的线性变换
１．在线性变换下状态方程的特性
设一组状态变量λ与另一组状态变量γ之间有
γ１ ＝ｐ１１λ１＋ｐ１２λ２＋… ＋ｐ１ｋλｋ
γ２ ＝ｐ２１λ１＋ｐ２２λ２＋… ＋ｐ２ｋλｋ

γｋ ＝ｐｋ１λ１＋ｐｋ２λ２＋… ＋ｐｋｋλ







ｋ
表示为矢量式为γ
→
＝Ｐ
→
λ
→
其中λ和γ为列矢量
γ＝
γ１
γ２

γ







ｋ
　　λ＝
λ１
λ２

λ







ｋ
　　Ｐ＝
ｐ１１ ｐ１２ … ｐ１ｋ
ｐ２１ ｐ２２ … ｐ２ｋ
  … 
ｐｋ１ ｐｋ２ … ｐ１














ｋ
λ经线性变换变成γ，则原状态方程也做相应的改变。设源基底下状态方程表示为
ｄ
ｄｔλ（ｔ）＝Ａλ＋Ｂｅ（ｔ）
经γ
→
＝Ｐ
→
λ
→
变换后
Ｐ－１ ｄｄｔγ（ｔ）＝ＡＰ
－１γ（ｔ）＋Ｂｅ（ｔ）
因而在新的状态变量下，状态方程与输出方程中的系数矩阵与原方程的系数矩阵有如下关系
Ａ^＝ＰＡＰ－１
Ｂ^＝ＰＢ
Ｃ^＝ＣＰ－１
Ｄ^







＝Ｄ
—８８１—
２．系统转移函数阵在线性变换下是不变的
状态方程和系统转移函数是描述系统的两种方法，当状态矢量用不同基底时，并不影响系统的物
理本质，因此对同一系统不同状态变量的选择，系统函数应是不变的。
证明：
Ｈ（ｓ）＝Ｃ^（ｓＩ－Ａ）－１Ｂ^＋Ｄ^＝ＣＰ－１（ｓＩ－ＰＡＰ－１）－１ＰＢ＋Ｄ
＝Ｃ［（ｓＩ－ＰＡＰ－１）Ｐ］－１ＰＢ＋Ｄ
＝Ｃ［Ｐ－１（ｓＩ－ＰＡＰ－１）Ｐ］－１Ｂ＋Ｄ
＝Ｃ（ｓＩ－Ａ）－１Ｂ＋Ｄ＝Ｈ（ｓ）
３．由状态方程判断系统的稳定性
特征值决定了系统的自由运动情况，因此可以根据Ａ矩阵的特征值来判断系统的稳定情况。
１）连续系统
判断连续系统是否稳定，只要定出Ａ的特征值Ｒｅ［ａｉ］是否小于零，即对稳定系统Ｒｅ［ａｉ］＜０。
判断上述情况需要求解方程｜ａＩ－Ａ｜＝０
方程｜ｓＩ－Ａ｜＝０的根在ｓ平面上的位置决定了系统的稳定情况，因为其与求解方程｜ａＩ－Ａ｜＝
０的特征根来判定系统稳定性是一致的。即只要知道根落在ｓ平面的左半平面，便可确定系统的稳定情
况，即判定Ｒｅ［ａｉ］＜０
２）离散系统
对于离散系统，根据Ａ矩阵的特征值｜ａｉ｜＜１判定。即系统的特征根位于单位圆内系统稳定。和连
续系统相似，Ａ矩阵的特征值和离散系统转移函数特征多项式的根位置相同，判定准则也相同。
七、系统的可控制性与可观测性
１）控制作用是否必然可以使系统在有限时间内，从起始状态指引到所要求状态，这就是可控制性
问题。
２）是否可以做到，通过观测有限时间内输出量，而识别系统的起始状态。
１．系统可控制性定义、可控阵满秩判别法
１）可控性：
当系统用状态方程描述时，给定系统的任意初始态，可以找到容许的输入量（即控制矢量），在有
限时间内把系统的所有状态引向状态空间的原点（即零状态），如果能做到这一点，则称系统是完全可
控制的。如果只对部分状态变量适用，则称系统不完全可控。
２）可控满秩判别法
设连续系统有ｋ个状态变量，则可用如下状态方程
λ
·
ｋ×１（ｔ）＝Ａｋ×ｋλｋ×１（ｔ）＋Ｂｋ×ｋｅ（ｔ）
它的解为
—９８１—
郑君里《信号与系统》考点精讲
λ（ｔ）＝ｅＡｔλ（０－）＋∫
ｔ
０
ｅＡ（ｔ－τ）Ｂｅ（τ）ｄτ
只要方程
ｅＡｔλ（０－）＋∫
ｔ
０
ｅＡ（ｔ－τ）Ｂｅ（τ）ｄτ＝０有解即可满足要求。
将上式改写为：λ（０－）＝－∫
ｔ
０
ｅ－ＡτＢｅ（τ）ｄτ
考虑到凯莱 －哈密顿定理，则有：
ｅ－Ａτ ＝∑
ｋ－１
ｉ＝０
ｃｉ（τ）Ａ
ｉ
代入上式有
λ（０－）＝－∑
ｋ－１
ｉ＝０
ＡｉＢ∫
ｔ１
０－
ｃｉ（τ）ｅ（τ）ｄτ
令ωｉ（ｔ１） ＝∫
ｔ１
０－
ｃｉ（τ）ｅ（τ）ｄτ
则上式可写成
λ（０－）＝－∑
ｋ－１
ｉ＝０
ＡｉＢωｉ（ｔ１）
＝－（Ｂ　ＡＢ　…　Ａｋ－１Ｂ）
ω０（ｔ１）
ω１（ｔ１）
…
ωｋ－１（ｔ１













）
Ａ为非奇异矩阵，若系统状态完全可控，也就是给定一组起始状态 λ（０－），满足之前方程，则必
须有：
Ｍ ＝［Ｂ ＡＢ Ａ２Ｂ … Ａｋ－１Ｂ］
满秩。这就是连续系统完全可控的充要条件。
Ｍ称为系统的可控性判别矩阵，简称可控阵，在给定系统状态方程时，只要Ｍ阵满秩，系统即为完
全可控系统
２．系统的可观性定义，可观阵满秩判别法
１）系统的可观测性：
如果系统用状态方程描述，在给定控制后，能在有限时间间隔内根据系统输出唯一地确定系统的
所有起始状态，则称系统完全可观；若只能确定部分起始状态，则称系统不完全可观。
２）可观阵满秩判别法
设连续时间系统有ｋ个状态变量，则系统的输出可写作：
ｒ（ｔ）＝ＣｅＡｔλ（０－）＋［Ｃｅ
ＡｔＢ＋Ｄδ（ｔ）］ｅ（ｔ）
令ｅ（ｔ）＝０，这样有：
—０９１—
ｒ（ｔ）＝ＣｅＡｔλ（０－）
或按凯莱 －哈密顿定理可写成
ｒ（ｔ）＝Ｃ（ｃ０Ｉ＋ｃ１Ａ＋Λ＋ｃｋ－１Ａ
ｋ－１）λ（０－）
上式表明输出量是系统所有起始状态的线性组合。
ｒ（ｔ）＝［ｃ０ ｃ１ Λ ｃｋ－１］
Ｃ
ＣＡ
Ｍ
ＣＡｋ－











１
λ（０－）
因而要在０＜ｔ＜ｔ０时间间隔内，根据输出量唯一确定起
始状态必须使矩阵
Ｎ＝
Ｃ
ＣＡ
…
ＣＡｋ－











１
有Ｋ个线性无关列向量，亦即上阵满秩。这是连续系统可观的充要条件。Ｎ称为系统的可观阵，在
给定系统时，只要Ｎ阵满秩，则系统为完全可观系统。
—１９１—
郑君里《信号与系统》考点精讲