概要信息：

阎石《数字电子技术基础》考点精讲
考核的性质及要求
考试的性质：笔试，通过适当比例的基本题，中等难度及较高难度题，考察应试者对基本概念，基
本知识的掌握能力，对运用基本理论知识分析设计电路的能力，以及应用基本理论知识解决实际问题
的能力。
１．掌握数字电子技术的基本概念和基本知识．
２．掌握基本的逻辑电路分析及设计方法。
３．器件的基本特性，基本分析方法，应用方法及设计方法。
４．具有较强的知识拓展能力，能分析及设计综合的逻辑电路
考核的方式
多数高校是和模拟电子技术基础合在一起放在一张试卷上来考，称为“电子技术”。各占７５分，
满分为１５０分，但由于研究生阶段所研究的专业，方向等有所不同，所以对数字电子技术基础这门课
程的要求程度也有所不同，因此也有单独来考数字电子技术基础的。
例如：深圳大学的生物医学工程就是将数字电子技术基础单独来作为一门专业课考查的。考察
的方式比较多样，甚至有的学校还将数电和电路，信号系统，通信原理等课程中的一门或两门合在一
张试卷上考察，当然分值的比例也就有所不同，视各高校及专业的不同而不同。
考试题型分析
１．选择题：
考查学生对基本概念的理解和基本知识的掌握程度
２．填空题：
考查学生对基本知识的掌握和基本电路的分析能力
３．判断题：
考查学生对容易混淆的概念，公式，定理的掌握程度
４．分析设计题：
—１—
阎石《数字电子技术基础》考点精讲及复习思路
考查学生对节本理论和分析设计方法的综合应用
《数字电子技术基础》的复习方法
１．注重掌握基本概念、基本原理、基本分析和设计方法我们要学习的不是各种电路的简单罗列，
不是死记硬背各种电路，而是要掌握它们的基本概念、基本原理、基本分析与设计方法。只有这样才
能对给出的任何一种电路进行分析，或者根据要求设计出满足实际需要的数字电路。
２，注意归纳总结
需要掌握一些典型电路，因为这些典型电路是构成数字系统的部件。掌握它们包括了解它们的
功能、结构特点及应用背景，并注意总结归纳，掌握其本质。例如，译码器和数据选择器都可以实现逻
辑函数，但两者的区别是，一个 ｎ位二进制输入端的译码器，只能用于产生变量数不大于 ｎ的组合逻
辑函数，它可以附加门电路，实现多个输出的组合逻辑电路；一个ｎ个地址输人端的数据选择器，可以
实现变量数＞ｎ的逻辑函数。由于数据选择器只有一个输出端，所以只能实现单个输出的逻辑函数。
３，抓重点，注重掌握功能部件的外特性数字集成电路的种类很多，各种电路的内部结构及内部工
作过程千差万别，特别是大规模集成电路的内部结构更为复杂。学习这些电路时，不可能也没有必要
一一记住它们，主要是了解电路结构特点及工作原理，重点掌握它们的外部特性（主要是输入和输出
之间的逻辑功能）和使用方法，并能在此基础上正确地利用各类电路完成满足实际需要的逻辑设计。
４．多做练习，多做真题．
章节分析
数制和码制
（１）二、十六进制、十进制及其他们的相互转换。
（２）掌握十进制代码；熟悉格雷码及奇偶校验码。
逻辑代数基础
（１）逻辑代数的基本运算
（２）逻辑代数的基本公式与定理
（３）逻辑函数的各种表示方法
（４）逻辑代数的公式化简法，卡诺图化简法
门电路
（１）掌握正逻辑和负逻辑的概念。
（２）掌握各种门电路的性能和表示方法
（３）了解ＴＴＬ和ＣＭＯＳ门电路的外部特性
（４）若干电参数的物理意义：ＶＯＨ、ＶＯＬ、ＶＩＨ等
—２—
考试点（ｗｗｗ．ｋａｏｓｈｉｄｉａｎ．ｃｏｍ）名师精品课程　电话：４００－６８８５－３６５
组合逻辑电路
（１）组合逻辑电路的特点及描述方法
（２）掌握用ＳＳＩ分析与设计组合逻辑电路的基本方法
（３）掌握常用的ＭＳＩ组合功能部件的逻辑功能、性能拓展及使用方法
（４）定性了解竞争———冒险产生的原因及消除方法
触发器
（１）ＲＳ、Ｄ、ＪＫ、Ｔ型触发器的逻辑功能、描述方法及触发器逻辑功能的转换。
（２）复位、置位端的应用（注意是异步还是同步）
（３）会画不同类型，不同结构的触发器的时序波形图
时序逻辑电路
（１）时序逻辑电路的特点及描述方法
（２）掌握同步时序逻辑电路和异步计数器的基本分析方法
（３）掌握同步时序逻辑电路的基本设计方法（ＳＳＩ）
（４）掌握常用ＭＳＩ时序逻辑器件的逻辑功能及使用方法
（５）电路能否自启动分析。
脉冲波形的产生与整形
（１）由５５５定时器构成的施密特触发器、单稳态触发器、多谐振荡器的工作原理、波形分析和计算
（２）若干电参数的物理意义：ＶＴ＋、ＶＴ－、ＴＷ、ＴＣＰ、ｆＣＰ等
半导体存储器
（１）ＲＯＭ、ＲＡＭ的结构及分析，存储容量的计算
（２）用存储器实现组合逻辑函数
（３）存储器容量的扩展
ＤＡＣ与ＡＤＣ
（１）ＤＡＣ的组成：权电阻，倒Ｔ型、权电流ＤＡＣ的工作原理和特点，转换误差分析、ＶＯ的计算
（２）ＡＤＣ的组成：并联型，计数型、逐次—渐进型、双积分型ＡＤＣ的结构及性能比较
（３）ＤＡＣ和ＡＤＣ的分辨率的计算
—３—
阎石《数字电子技术基础》考点精讲及复习思路
第１讲　数制与编码
考点：
１．常用数（二进制、十进制、八进制）的表示。及它们之间的相互转换
２．常用编码的表示
８４２１ＢＣＤ码　　５４２１ＢＣＤ码
２４２１ＢＣＤ码　　余三ＢＣＤ码
格雷码　　奇偶校验码
所占分数不多，１分到２分。有的学校不考，但后面的题要用到这一章的概念
数制：多位数码中的每一位数的构成及低位向高位进位的规则
（一）十进制
十进制：十进制采用０，１，２，３，４，５，６，７，８，９十个数码，其进位的规则是“逢十进一”
十进制数的展开式
４５８７．２９＝４
!
１０３＋５
!
１０２＋８
!
１０１＋７
!
１００＋２
!
１０"１＋９
!
１０"２
一般表达式：
（Ｎ）Ｄ＝∑
#
ｉ＝－
#
Ｋｉ×１０
ｉ
各位的权都是１０的幂
任意进制数的一般表达式为：（Ｎ）ｒ＝∑
#
ｉ＝－
#
Ｋｉ×ｒ
ｉ
十进制是人们最熟悉的数，但实现较困难
（二）二进制
二进制数的表示方法：
二进制数只有０、１两个数码。用两个状态即可表示，容易实现。进位规律是：“逢二进一”
例：１＋１＝１０＝１×２１＋０×２０
二进制数一般表达式为：
（Ｎ）Ｂ＝∑
#
ｉ＝－
#
Ｋｉ×２
ｉ
各位的权都是２的幂。
—４—
考试点（ｗｗｗ．ｋａｏｓｈｉｄｉａｎ．ｃｏｍ）名师精品课程　电话：４００－６８８５－３６５
１０１０１．１０１＝１
!
２４＋１!２２＋１
!
２０＋１
!
２－１＋１
!
２－３＝２１．６２５
二进制书写较长，易出错．为压缩二进制书写长度，采用十六进制和八进制。
（三）八进制和十六进制
１．八进制
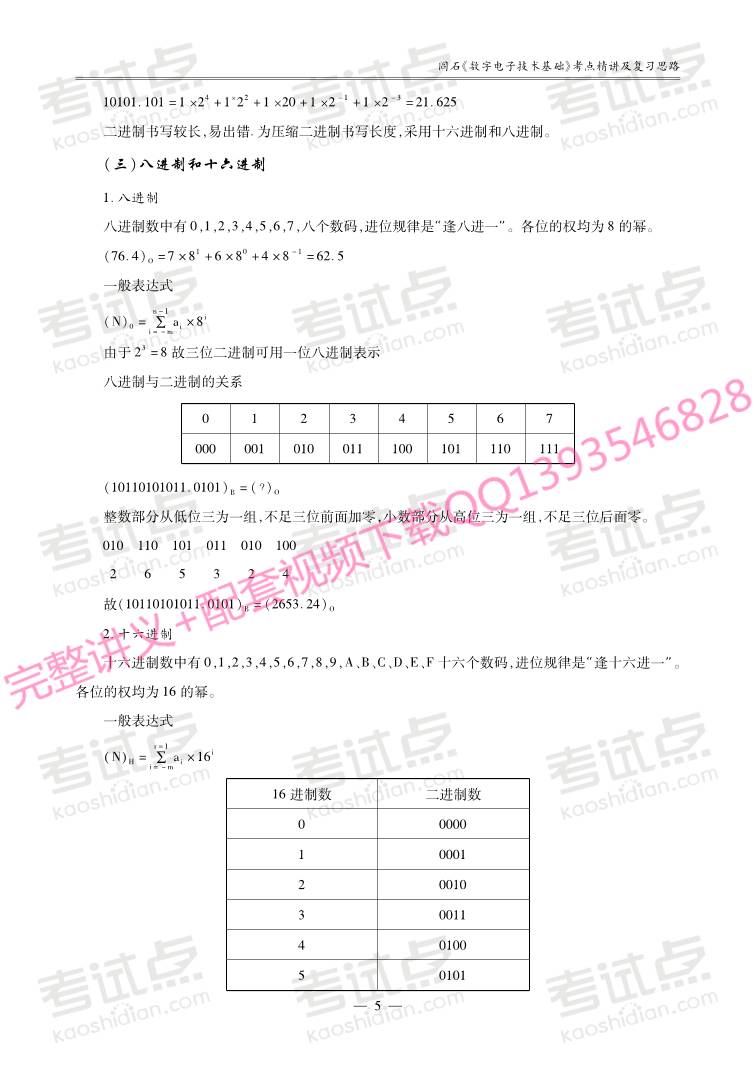
八进制数中有０，１，２，３，４，５，６，７，八个数码，进位规律是“逢八进一”。各位的权均为８的幂。
（７６．４）Ｏ＝７×８
１＋６×８０＋４×８－１＝６２．５
一般表达式：
（Ｎ）０＝∑
ｎ－１
ｉ＝－ｍ
ａｉ×８
ｉ
由于２３＝８故三位二进制可用一位八进制表示
八进制与二进制的关系
０ １ ２ ３ ４ ５ ６ ７
０００ ００１ ０１０ ０１１ １００ １０１ １１０ １１１
（１０１１０１０１０１１．０１０１）Ｂ＝（？）Ｏ
整数部分从低位三为一组，不足三位前面加零；小数部分从高位三为一组，不足三位后面零。
０１０ １１０ １０１ ０１１ ０１０ １００
２ ６ ５ ３ ２ ４
故（１０１１０１０１０１１．０１０１）Ｂ＝（２６５３．２４）Ｏ
２．十六进制
十六进制数中有０，１，２，３，４，５，６，７，８，９，Ａ、Ｂ、Ｃ、Ｄ、Ｅ、Ｆ十六个数码，进位规律是“逢十六进一”。
各位的权均为１６的幂。
一般表达式：
( )ＮＨ＝∑
ｒ＝１
ｉ＝－ｍ
ａｉ×１６
ｉ
１６进制数 二进制数
０ ００００
１ ０００１
２ ００１０
３ ００１１
４ ０１００
５ ０１０１
—５—
阎石《数字电子技术基础》考点精讲及复习思路
１６进制数 二进制数
６ ０１１０
７ ０１１１
８ １０００
９ １００１
Ａ １０１０
Ｂ １０１１
Ｃ １１００
Ｄ １１０１
Ｅ １１１０
Ｆ １１１１
各位的权都是１６的幂。
由于２４＝１６故四位二进制可用一位１６进制表示。对应关系如表所示。这样长度可压缩到二进
制数长度的四分之一。
１６进制与二进制的关系表
Ａ６．Ｃ＝１０×１６１＋６×１６０＋１２×１６－１＝１６０＋６＋０．７５＝１６６．７５
这样１６进制数的长度可压缩到二进制数长度的四分之一
（１０１１０１０１０１１．０１０１）Ｂ＝（？）Ｈ
整数部分从低位四为一组，不足四位前面加零；小数部分从高位四为一组，不足四位后面加零。
０１０１ １０１０ １０１１ ０１０１
５ Ａ Ｂ ５
（１０１１０１０１０１１．０１０１）Ｂ＝（５ＡＢ．５）Ｈ
１６进制数 二进制数
０ ００００
１ ０００１
２ ００１０
３ ００１１
４ ０１００
５ ０１０１
—６—
考试点（ｗｗｗ．ｋａｏｓｈｉｄｉａｎ．ｃｏｍ）名师精品课程　电话：４００－６８８５－３６５
１６进制数 二进制数
６ ０１１０
７ ０１１１
８ １０００
９ １００１
Ａ １０１０
Ｂ １０１１
Ｃ １１００
Ｄ １１０１
Ｅ １１１０
Ｆ １１１１
（四）数制间的转换
１．十———二转换
①整数部分用“辗转相除”法：
【例】：将十进制数６５转换为二进制数：
所以（６５）Ｄ＝（１０００００１）Ｂ
②小数部分：乘２法
乘２法；将十进制数的小数部分乘２，取其整数得Ｄ－１，；再将小数部分乘２，取其整数得Ｄ－２；再将
小数部分乘２…
【例】：将十进制数０．６２５转换为二进制数：
０．６２５　
　×　　２　
１．２５０　
→　 　整数部分＝１＝Ｄ－１
—７—
阎石《数字电子技术基础》考点精讲及复习思路
０．２５０　
　×　　２　
０．５００　
→　 　整数部分＝０＝Ｄ－２
０．５００　
　×　　２　
１．０００　
→　 　整数部分＝１＝Ｄ－３
所以（０．６２５）Ｄ＝（０．１０１）Ｂ
２．二———十转换
方法：按二进制展开式展开，即将每位的系数乘以该位的权值，然后各项乘积相加，就可得到等值
的十进制数
【例】：将二进制数１０１．１１转换为十进制数：
（１０１．１１）２＝１×２
２＋０×２１＋１×２０＋１×２－１＋１×２－２
＝４＋０＋１＋０．５＋０．２５
＝５．７５
３．二———十六进制之间的转换
①二进制转换成十六进制：
因为１６进制的基数１６＝２４，所以，可将四位二进制数表示一位１６进制数，即００００～１１１１表示０
－Ｆ。
方法：从低位到高位将每４位二进制数分为一组，并将每一组以等值的十六进制数代之，即可得
到对应的十六进制数。
（０１０１ ０００１ １０１１）


 Ｂ
　↓ ↓ ↓


 　
（５ １ Ｂ）Ｈ
②十六进制转换成二进制：
方法：将每位１６进制数展开成四位二进制数，排列顺序不变即可。
【例】：将十六进制数８ＦＣ６转换为二进制数：
（ ８ Ｆ Ｃ ６ ）Ｈ
↓ ↓ ↓ ↓
（ １０００ １１１１ １１００ ０１１０ ）Ｂ
—８—
考试点（ｗｗｗ．ｋａｏｓｈｉｄｉａｎ．ｃｏｍ）名师精品课程　电话：４００－６８８５－３６５
例题：（１５６）Ｄ对应的八进制数是（　　）
Ａ．（１５６）Ｏ　　　　　　　　　　　　　　　　Ｂ．（２３４）Ｏ
Ｃ．（４７０）Ｏ Ｄ．（５６１）Ｏ
此题考核数制间的转换。具体过程可除８取余或先转成二进制，再由二进制转为八进制。
正确选项为【Ｂ】
例题：下列各数中最大的数是（　　）
Ａ．（３７）Ｈ Ｂ．（３７）Ｄ
Ｃ．（３７）Ｏ Ｄ．（４０）Ｏ
本题仍然是考核数制的转换，将其转换为十进制，再进行比较。
正确选项为【Ａ】
【２０１１年———北京科技大学】
十进制数（２６．６２５）１０的二进制数是（　　）
Ａ．（１１０１０．１０１） Ｂ．（１００１０．１０１）
Ｃ．（１１００１．１０１） Ｄ．（１１０１０．１００）
【２００９年———浙江理工】
将二进制数（１０１０１０１．００１１）分别转换成下列进制数
十进制数 ，八进制 ，十六进制数 。
编码
由于数字系统只认可二进制代码组成的信息。所以对数字系统的信息均要用二进制代码表示。
编码———用二进制代码表示特定信息的过程。
（一）二～十进制代码（ＢＣＤ码）
十进制人们最熟悉，而机器只认识二进制代码，用二进制代码表示十进制数（ＢｉｎａｒｙＣｏｄｅｄＤｅｃｉ
ｍａｌ）简称ＢＣＤ，由于２３＝８＜１０＜２４＝１６，所以表示一位十进制至少需要四位二进制。而四位二进制
有十六种状态，从１６中任取十个状态即可组成十进制数共有２．９×１０１０种方案。
常用的有：有权码和无权码
有权码———即每位有固定的权值；
如：８４２１ＢＣＤ，５４２１ＢＣＤ，２４２１ＢＣＤ等；
无权码———即每位无固定的数值
如：余３ＢＣＤ码、格雷 ＢＣＤ码等。余 ３ＢＣＤ码和 ８４２１ＢＣＤ的关系是：８４２１ＢＣＤ加 ００１１等于余
３ＢＣＤ码。
求ＢＣＤ代码表示的十进制数
对于有权ＢＣＤ码，可以根据位权展开求得所代表的十进制数。
—９—
阎石《数字电子技术基础》考点精讲及复习思路
例如：
［０１１１］８４２１ＢＣＤ码 ＝０×８＋１×４＋１×２＋１×１＝（７）Ｄ
［１１０１］２４２１ＢＣＤ码 ＝１×２＋１×４＋０×２＋１×１＝（７）Ｄ
用ＢＣＤ代码表示十进制数
对于一个多位的十进制数，需要有与十进制位数相同的几组ＢＣＤ代码来表示。
例如：
( )４６３．５１０＝
０１００
４
０１１０
６
００１１
３
０１０１[ ]５ ８４２１ＢＣＤ
( )８６３．２１０＝
１１１０
８
１１００
６
００１１
３
００１０[ ]２ ２４２１ＢＣＤ
例题：（３８．５）Ｄ的余３ＢＣＤ码是（　　）
Ａ．（０１１０１０１１．１０００）余３ＢＣＤ Ｂ．（００１１１０００．０１０１）余３ＢＣＤ
Ｃ．（００１１１０１１．１０００）余３ＢＣＤ Ｄ．（００１１１１１０．１０１１）余３ＢＣＤ
本题考核各种常用的编码。
正确选项为【Ａ】
例题：（７６）Ｏ的８４２１ＢＣＤ码是（　　）
Ａ．（０１１１０１１０）８４２１ＢＣＤ Ｂ．（０１１０００１０）８４２１ＢＣＤ
Ｂ．（１０１０１００１）８４２１ＢＣＤ Ｄ．（１１０１１１００）８４２１ＢＣＤ
本题最易出错：选中［Ａ］其错误的原因是ＢＣＤ是表示十进制数，是按逢十进一的进位关系进位，
（０１１１０１１０）８４２１ＢＣＤ是表示七十六，而（７６）Ｏ＝７×８
１＋６×８０＝６２，是六十二，所以正确选项为［Ｂ］。
（二）可靠性编码
代码在产生和传输的过程中，难免产生错误，为减少错误的产生，或者能检测出错误的发生，故广
泛采用了可靠性编码技术。
１．格雷码（Ｇｒａｙ）
前述的代码中相邻两组代码中存在多位变化而每位变化速度不同，将会产生错误的中间状态
如８４２１ＢＣＤ码，当０１１１→１０００时，假设高位先变，则过程如下：
０１１１→１１１１→１０１１→
       
１００１
错误的中间状态
→１０００
在某些控制系统中，绝对不允许出现此种现象，为此出现格雷码（又称循环码）。格雷码的特征
是，每相邻两组代码仅有一位发生变化－即相邻两组代码的码距为１。它属于无权码。
二位格雷码
—０１—
考试点（ｗｗｗ．ｋａｏｓｈｉｄｉａｎ．ｃｏｍ）名师精品课程　电话：４００－６８８５－３６５
００
０１
１１
１０
三位格雷码
０００
００１
０１１

　　０１０　　
１１０
１１１
１０１
１００
低四位将二位格雷码前加一位０，高位对折，将高位的０变为１
同理可得四位格雷码
００００
０００１
００１１
００１０
０１１０
０１１１
０１０１

　　０１００　　
１１００
１１０１
１１１１
１１１０
１０１０
１０１１
１００１
１０００
由于相邻两组代码仅有一位变化，故不会产生错误的中间状态
—１１—
阎石《数字电子技术基础》考点精讲及复习思路
二进制码
ｂ３ｂ２ｂ１ｂ０
格雷码
Ｇ３Ｇ２Ｇ１Ｇ０
００００ ００００
０００１ ０００１
００１０ ００１１
００１１ ００１０
０１００ ０１１０
０１０１ ０１１１
０１１０ ０１０１
０１１１ ０１００
１０００ １１００
１００１ １１０１
１０１０ １１１１
１０１１ １１１０
１１００ １０１０
１１０１ １０１１
１１１０ １００１
１１１１ １０００
２．奇偶校验码
信号代码传递过程中，由于干扰等原因产生错误
如：１０００
　信号传输过程中干扰原因
→
　
１１００
如不能发现错误，其结果显然是错误的，这样设备的可靠性将很低。
为此出现多种编码方式。最常用的是奇偶校验码。即在数据码的基础上增加一位校验位，使得
“１”的个数为奇数称奇效验码如为偶数个“１”称偶校验码。接受代码时检测“１”的个数，如与发射的
代码不符即为错码。８４２１ＢＣＤ奇偶校验码如右表：
信息码 奇校位 偶校位
０ ００００ １ ０
１ ０００１ ０ １
２ ００１０ ０ １
—２１—
考试点（ｗｗｗ．ｋａｏｓｈｉｄｉａｎ．ｃｏｍ）名师精品课程　电话：４００－６８８５－３６５
信息码 奇校位 偶校位
３ ００１１ １ ０
４ ０１００ ０ １
５ ０１０１ １ ０
６ ０１１０ １ ０
７ ０１１１ ０ １
８ １０００ ０ １
９ １００１ １ ０
【２００７年—华南理工】
下列四个数中最大的数是（　　）
Ａ．（ＡＦ）１６ Ｂ．（００１０１０００００１０）８４２１ＢＣＤ
Ｃ．（１０１０００００）２ Ｄ．（１９８）１０
【２００５—华南理工】
计算按下列各式
１．求与（１ＣＥ８）１６等值得１０进制数
２．求与（４３８）８等值得８４２１ＢＣＤ码
３．求在哪一种数制中槡４１＝５成立
—３１—
阎石《数字电子技术基础》考点精讲及复习思路
第２讲　基本逻辑运算
与常用复合逻辑（１）
考点：
１．三种基本逻辑运算功能
２．常用复合逻辑功能
功能包含：真值表、逻辑函数表达式、逻辑符号、波形关系
该讲直接作为考研题的不多，但它是逻辑电路的基础。这部分不掌握后面部分很难深入。故本
部分虽然不直接作为考题。但以后的考题要涉及到本部分内容。
二值逻辑变量与基本逻辑运算
逻辑运算：
逻辑问题都是二值性的。当０和１表示逻辑状态时，两个二进制数码按照某种特定的因果关系
进行的运算。逻辑运算使用的数学工具是逻辑代数。
逻辑代数与普通代数：
与普通代数不同之处是逻辑代数中的变量只有０和１两个可取值，它们分别用来表示完全两个
对立的逻辑状态。
在逻辑代数中，有与、或、非三种基本的逻辑运算。
逻辑运算的描述方式：
逻辑代数表达式、真值表、逻辑图、卡诺图、波形图和硬件描述语言（ＨＤＬ）等。
一、三种基本逻辑运算
１．与运算
①与逻辑：只有当决定某一事件的条件全部具备时，这一事件才会发生。这种因果关系称为与逻
辑关系。
与逻辑符号
—４１—
考试点（ｗｗｗ．ｋａｏｓｈｉｄｉａｎ．ｃｏｍ）名师精品课程　电话：４００－６８８５－３６５
逻辑表达式：与逻辑：Ｌ＝Ａ·Ｂ＝ＡＢ
与逻辑的波形图：
２．或运算
在决定某一事件的各种条件中，有一个或几个条件具备时，这一事件就会发生。这种因果关系称
为或逻辑关系。
或逻辑符号：
逻辑表达式：或逻辑：Ｌ＝Ａ＋Ｂ
３．非运算
事件发生的条件具备时，事件不会发生；事件发生的条件不具备时，事件发生。这种因果关系称
为非逻辑关系。
非逻辑符号：
逻辑表达式Ｌ＝Ａ′＝Ａ
－
二、几种常用复合逻辑运算
１．与非运算
“与”逻辑和“非”逻辑的组合。先“与”再“非”。
—５１—
阎石《数字电子技术基础》考点精讲及复习思路
与非逻辑符号：
与非逻辑表达式
Ｌ＝（ＡＢ）′＝ＡＢ
波形图
真值表
２．或非运算
“或”逻辑和“非”逻辑的组合。先“或”再“非”。
或非逻辑符号
或非逻辑表达式
Ｌ＝（Ａ＋Ｂ）′＝Ａ＋Ｂ
波形关系
３．与或非
图形符号：
与或非逻辑表达式：
—６１—
考试点（ｗｗｗ．ｋａｏｓｈｉｄｉａｎ．ｃｏｍ）名师精品课程　电话：４００－６８８５－３６５
Ｙ＝（ＡＢ＋ＣＤ）′＝ＡＢ＋ＣＤ
４．“异或”“同或”逻辑
这是具有特殊功能的逻辑，它们的定义均是对二变量而言。
①“异或”“同或”逻辑
输入二变量相异为“１”，相同为“０”，称为“异或”Ｆ１。
输入二变量相异为“０”，相同为“１”，称为“同或”Ｆ２。
其真值表如下：
Ａ Ｂ Ｆ２ Ｆ１
０ ０ ０ １
０ １ １ ０
１ ０ １ ０
１ １ ０ １
由真值表可得出下式：
异或
Ｆ１＝Ａ′Ｂ＋ＡＢ′＝Ａ
－
Ｂ＋ＡＢ
－
＝ＡＢ
同或
Ｆ２＝Ａ′Ｂ′＋ＡＢ＝Ａ
－
Ｂ
－
＋ＡＢ＝Ａ⊙Ｂ
由真值表可得出下式：
可看出异或、同或互为反函数
ＡＢ＝（ＡＢ）′＝Ａ⊙Ｂ
或ＡＢ＝Ａ⊙Ｂ＝（Ａ⊙Ｂ）′
即Ａ
－
Ｂ＋ＡＢ
－
＝Ａ
－
Ｂ
－
＋ＡＢ
（Ａ′Ｂ＋ＡＢ′）′＝Ａ′Ｂ′＋ＡＢ
或Ａ
－
Ｂ
－
＋ＡＢ＝Ａ
－
Ｂ＋ＡＢ
－
（Ａ′Ｂ′＋ＡＢ）′＝Ａ′Ｂ＋ＡＢ′
ＡＢ＝（ＡＢ）′＝Ａ⊙Ｂ
或ＡＢ＝Ａ⊙Ｂ＝（Ａ⊙Ｂ）′
即Ａ
－
Ｂ＋ＡＢ
－
＝Ａ
－
Ｂ
－
＋ＡＢ
（Ａ′Ｂ＋ＡＢ′）′＝Ａ′Ｂ′＋ＡＢ
或Ａ
－
Ｂ
－
＋ＡＢ＝Ａ
－
Ｂ＋ＡＢ
－
—７１—
阎石《数字电子技术基础》考点精讲及复习思路
（Ａ′Ｂ′＋ＡＢ）′＝Ａ′Ｂ＋ＡＢ′
异或逻辑符号
②多变量的“异或”
由于不存在多变量的“异或”电路，故多变量的“异或”通
过二变量“异或”实现。例如：Ｆ＝ＡＢＣＤ
Ｆ＝Ｆ１Ｆ２　　Ｆ２＝ＣＤ
将其代入Ｆ表达式得：Ｆ＝ＡＢＣＤ
波形关系
—８１—
考试点（ｗｗｗ．ｋａｏｓｈｉｄｉａｎ．ｃｏｍ）名师精品课程　电话：４００－６８８５－３６５
第３讲　基本逻辑运算
与常用复合逻辑（２）
“异或”电路的特殊功能
００＝０　０１＝１　１０＝１
１１＝１　０Ａ＝Ａ　１Ａ＝Ａ
－
＝Ａ′
故可十分方便得Ａ，Ａ
－
控制电路如下图所示：
奇偶检测电路
奇数个“１”相异或结果为“１”。
偶数个“１”相异或结果为“０”。
利用此特性，可十分方便组成“奇偶校验位”的产生电路，也可十分方便组成奇偶校８４２１ＢＣＤ“奇
校验位产生电路”和“校验码检测电路”如下图所示：
—９１—
阎石《数字电子技术基础》考点精讲及复习思路
三、逻辑函数的表示方法
常用的表示方法
１．逻辑真值表
２．逻辑函数式（逻辑式或函数式）
３．逻辑图
４．卡诺图（在后面介绍）
５．波形图（时序图）
１．逻辑真值表表示：：逻辑抽象，列出真值表
将输入变量所有的取值下对应的输出值找出来列成表格，即可得到真值表。
【例】：三人表决电路：三人Ａ、Ｂ、Ｃ当中有两人或两人以上同意时，表决结果 Ｙ为通过，否则表决
结果Ｙ为没通过，决结果Ｙ的状态（通过与没通过）是三人Ａ，Ｂ，Ｃ状态（同意与不同意）的函数。
逻辑函数为：Ｙ＝Ｆ（Ａ，Ｂ，Ｃ）
输入变量为１表示同意，０表示不同意，输出（函数）Ｙ为１表示通过，０表示没通过。
三人表决真值表
Ａ Ｂ Ｃ Ｙ
０ ０ ０ ０
０ ０ １ ０
０ １ ０ ０
０ １ １ １
１ ０ ０ ０
１ ０ １ １
１ １ ０ １
１ １ １ １
２．各种方法间的互相转换
①从真值表写出逻辑函数式
一般方法：
（１）找出真值表中使逻辑函数为１的那些输入变量取值的组合。
（２）每组输入变量取值的组合对应一个乘积项，其中取值为１的写入原变量，取值为０的写入反
变量。
（３）将这些乘积项相加，即得输出的逻辑函数式。
②从真值表写出逻辑函数式
—０２—
考试点（ｗｗｗ．ｋａｏｓｈｉｄｉａｎ．ｃｏｍ）名师精品课程　电话：４００－６８８５－３６５
一般方法：将输入变量取值的所有组合状态逐一代入逻辑式，求出函数值，列成表。
【例】：将下图所示真值表转换为逻辑函数式。
Ａ Ｂ Ｃ Ｌ
０ ０ ０ ０
０ ０ １ ０
０ １ ０ ０
０ １ １ １
１ ０ ０ ０ →Ａ
－
ＢＣ＝Ａ′ＢＣ
１ ０ １ １ →ＡＢ
－
Ｃ＝ＡＢ′Ｃ
１ １ ０ １ →ＡＢＣ
－
＝ＡＢＣ′
１ １ １ １ →ＡＢＣ
Ｌ＝Ａ
－
ＢＣ＋ＡＢ
－
Ｃ＋ＡＢＣ
－
＋ＡＢＣ＝Ａ′ＢＣ＋ＡＢ′Ｃ＋ＡＢＣ′＋ＡＢＣ
③根据逻辑表达式画出逻辑图
一般方法：将逻辑函数中各变量之间的与、或、非等逻辑关系，用图形符号表示出来，就可画出表
示函数关系的逻辑图。
Ｌ＝Ａ
－
Ｂ
－
＋ＡＢ
④从逻辑图写出逻辑表达式
一般方法：从输入端到输出端逐级写出每个图形符号对应的逻辑式，即可得到对应的逻辑式。
Ａ
－
Ｂ＝Ａ′Ｂ
Ａ
－
Ｂ＋Ｂ
－
＋ＢＣ
－
＝（Ａ′Ｂ＋Ｂ′＋ＢＣ′）′
ＢＣ
－
＝ＢＣ′
Ｙ＝Ａ
－
Ｂ＋Ｂ
－
＋ＢＣ
－
＋ＢＣ
－
＝（Ａ′Ｂ＋Ｂ′＋ＢＣ′）′＋ＢＣ′
—１２—
阎石《数字电子技术基础》考点精讲及复习思路
⑤根据真值表画波形图
一般方法：将真值表中的变量和函数的对应值分别用高、低电平表示
真值表
Ａ Ｂ Ｌ
０ ０ １
０ １ ０
１ ０ ０
１ １ １
　 　
　
例：异或函数的几种表达方式
逻辑符号：
异或逻辑真值表
Ａ Ｂ ＬＢ
０ ０ ０
０ １ １
１ ０ １
１ １ ０
逻辑函数表达式Ｌ＝ＡＢ
—２２—
考试点（ｗｗｗ．ｋａｏｓｈｉｄｉａｎ．ｃｏｍ）名师精品课程　电话：４００－６８８５－３６５
四、关于使用集成电路的有关问题
前面已讲过集成电路分为双极性型即ＴＴＬ电路和单极性 ＭＯＳ电路。一般以 ＴＴＬ电路为主讲述
有关问题。
１．特性和参数
ＴＴＬ与非门传输特性如图所示
（１）输出高电平ＵＯＨ标值为３Ｖ，大于２．７Ｖ为合格。最高可达到３．６Ｖ。
（２）输出低电平ＵＯＬ标称值为０．３Ｖ一般认为小于０．３５Ｖ为合格。
（２）开门电平ＵＯＮ和关门电平Ｖｏｆ
开门电平：
输出低电平时与非门处于开门状态，为保证输出低电平低于０．３５Ｖ，允许输入高电平的最小值称
为开门电ＵＯＮ；
关门电平：
输出为高电平时与非门处于关门状态，为保证输出高电平高于２．７Ｖ，允许输入低电平的最高值
称为关门电平Ｖｏｆ；
（３）噪声容限ＵＮＬ和ＵＮＨ
此参数是用来说明门电路的抗干扰能力的。
输入低电平时，输出应为高电平，如果此时输入端在低电平基础上叠加一个正向干扰信号，如超
过Ｕｏｆ时，输出将低于所规定高电平值，产生逻辑错误。所允许的最大干扰信号幅度称为输入低电平
时的噪声容ＵＮＬ。
ＵＮＬ＝Ｕ０ＦＦ－ＵＩＬ＝０．８－０．３＝０．５
—３２—
阎石《数字电子技术基础》考点精讲及复习思路
输入为高电平时，输出应为低电平，如果此时输入端在高电平基础上叠加一个负向干扰信号，如
低于ＵＯＮ时，输出将高于规定低电平值，产生逻辑错误。所允许最大干扰信号幅度称为输入高电平时
的噪声容限ＵＮＨ。
ＵＮＨ＝ＵＩＨ－ＵＯＮ＝３－１．８Ｖ＝１．２Ｖ
（４）输入短路电流ＩＩＳ
对ＴＴＬ门而言当输入端接地时，将有一个电流１．４毫安左右的电流由管子流出。
当输入通过电阻接地，ＩＩＳ将在电阻上产生电压，影响该输入端的状态。
一般为了保证输出为高电平输入端电阻满足：Ｒｉ≤０．７ＫΩ为了保证输出低电平
输入端电阻满足：Ｒｉ≥２ＫΩ
场效应管无输入短路电流，通过电阻接地时，输入始终是低电平。
（５）门电路的扇入系数ＮＩ和ＮＯ
门电路允许输入端数为扇入系数ＮＩ，一般ＮＩ≥８门，为保证门电路输出正确逻辑电平时，不超过
功耗的前提下，其输出端允许带动同类门的输入端数称为扇出系数，一般 ＮＯ≥８。ＮＯ愈大，表明门的
负载能力愈强。
输出开路门（ＯＣ门），就是门电路输出级集电极开路。因此使用时，输出端一定要外接电阻到直
流电源，该们才工作。否则该门不工作
电路符号如右图：
—４２—
考试点（ｗｗｗ．ｋａｏｓｈｉｄｉａｎ．ｃｏｍ）名师精品课程　电话：４００－６８８５－３６５
ＯＣ门使用时应注意两点：
①ＯＣ门使用时，输出端与电源间应接一个电阻，才能工作。
②ＯＣ门门并联使用时，完成逻辑与的功能通常称为“线与”功能。
Ｆ＝ＡＢ·ＣＤ＝ＡＢ＋ＣＤ＝（ＡＢ）′（ＣＤ）′＝（ＡＢ＋ＣＤ）′
２．三态门（ＴＳ门或ＴＳＬ门）
由于计算机ＣＰＵ采用总线结构，外设均挂在总线上，ＣＰＵ每一时刻仅能与一个外设交换信息，此
时其它外设必须与总线脱钩，使之不影响总线的状态。否则将破坏系统的正常工作，这就要求连接到
总线的接口电路必须具有三态结构，除了０态和１态外，还增加一个高阻态。其功能和逻辑图如下所
示。三态门可以是任何门我们仅以与非门、或门为例。
所有与总线相连的逻辑电路，必须是三态结构
【例７】：逻辑电路如图所示，其输出函数Ｆ为（　　）
Ａ．Ｃ＝０　Ｆ＝Ａ＋Ｂ　Ｃ＝１　Ｆ＝ＡＢ
Ｂ．Ｃ＝０　Ｆ＝０　Ｃ＝１　Ｆ＝１
Ｃ．Ｃ＝０　Ｆ＝Ａ＋Ｂ　Ｃ＝１　Ｆ＝ＡＢ
Ｄ．Ｆ＝ＡＢ·Ｃ
－
( )＋ Ａ＋ＢＣ
—５２—
阎石《数字电子技术基础》考点精讲及复习思路
第４讲　逻辑代数与
逻辑函数化简（１）
考点：这是考试的重点之一
１．基本公式
２．函数的代数法化简
３．函数的卡诺图化简
一、基本公式
表３－１　逻辑代数基本公式表
０Ａ＝０ １＋Ａ＝１
１Ａ＝Ａ ０＋Ａ＝Ａ
ＡＡ＝Ａ Ａ＋Ａ＝Ａ
ＡＡ′＝０ Ａ＋Ａ′＝１
ＡＢ＝ＢＡ Ａ＋Ｂ＝Ｂ＋Ａ
Ａ（ＢＣ）＝（ＡＢ）Ｃ Ａ＋（Ｂ＋Ｃ）＝（Ａ＋Ｂ）＋Ｃ
Ａ（Ｂ＋Ｃ）＝ＡＢ＋ＡＣ Ａ＋ＢＣ＝（Ａ＋Ｂ）（Ａ＋Ｃ）
（ＡＢ）′＝Ａ′＋Ｂ″ （Ａ＋Ａ）′＝Ａ′Ｂ′
Ａ＋ＡＢ＝Ａ Ａ（Ａ＋Ｂ）＝Ａ
ＡＢ＋ＡＢ′＝Ａ （Ａ＋Ｂ）（Ａ＋Ｂ′）＝Ａ
Ａ（Ａ′＋Ｂ）＝ＡＢ Ａ＋Ａ′Ｂ＝Ａ＋Ｂ
ＡＢ＋Ａ′Ｃ＋ＢＣ＝ＡＢ＋Ａ′Ｃ （Ａ＋Ｂ）（Ａ′＋Ｃ）（Ｂ＋Ｃ）＝（Ａ＋Ｂ）（Ａ′＋Ｃ）
由表可看出每个定律都是成对出现的，它们互为对偶式（关于对偶概念在基本法则将会介绍）．这
些定律可以直接代入“０”、“１”取值，也可用真值表加以验证。前６个比较直观，我们不证明了。其余
的我们证明对偶式中的一个即可。
分配律前一种形式与代数一样，易理解，后一种分配关系是加对乘的分配，是普通代数中没有的，
—６２—
考试点（ｗｗｗ．ｋａｏｓｈｉｄｉａｎ．ｃｏｍ）名师精品课程　电话：４００－６８８５－３６５
故又称为特殊分配律，它的正确性可用真值表验证，如表３－２所示
表３－２　证明分配律的真值表
ＡＢＣ Ｂ·Ｃ Ａ＋ＢＣ （Ａ＋Ｂ） （Ａ＋Ｃ） （Ａ＋Ｂ）（Ａ＋Ｃ）
０００ ０ ０ ０ ０ ０
００１ ０ ０ ０ １ ０
０１０ ０ ０ １ ０ ０
０１１ １ １ １ １ １
１００ ０ １ １ １ １
１０１ ０ １ １ １ １
１１０ ０ １ １ １ １
１１１ １ １ １ １ １
表明Ａ＋ＢＣ＝（Ａ＋Ｂ）（Ａ＋Ｃ）
吸收律１的证明，只证第二式
左式＝ＡＢ＋Ａ
－
Ｂ＝ＡＢ
－
( )＋Ｂ ＝Ａ因为Ｂ
－
( )＋Ｂ＝１
左式＝右式，证毕
吸收律２的证明，也只证第二式
( )Ａ＋ＡＢ＝Ａ１＋Ｂ ＝Ａ因为( )１＋Ｂ＝１ ( )证毕
吸收律３的证明，也只证第二式
Ａ＋ＡＢ＝ Ａ＋Ａ( )
－
( )Ａ＋Ｂ
＝Ａ＋Ｂ因为Ａ＋Ａ
－
( )＝１ ( )证毕
吸收律在逻辑函数化简中十分有用，定律１、２可将两项合并为一项，并消去一个变量；定律３可
将某些项中的部分因子消去。特别是吸收定律１是卡诺图化简的基础。
求反律（摩根）的真值表
ＡＢ Ａ＋Ｂ ＡＢ ＡＢ Ａ＋Ｂ
００ １ １ １ １
０１ ０ ０ １ １
１０ ０ ０ １ １
１１ ０ ０ ０ ０
多余项定律证明如下：
—７２—
阎石《数字电子技术基础》考点精讲及复习思路
ＡＢ＋Ａ
－
Ｃ＋ＢＣ
＝ＡＢ＋Ａ
－
Ｃ＋ＢＣ（Ａ＋Ａ
－
）
＝ＡＢ＋Ａ
－
Ｃ＋ＡＢＣ＋Ａ
－
ＢＣ
＝ＡＢ（１＋Ｃ）＋Ａ
－
Ｃ（１＋Ｂ）
＝ＡＢ＋Ａ
－
Ｃ
多余项定律可推广为：
ＡＢ＋Ａ
－
Ｃ＋ＢＣＥＦＧ＝ＡＢ＋Ａ
－
Ｃ
ＡＢ＋Ａ
－
Ｃ＋ＢＣＥＦＧ
＝ＡＢ＋Ａ
－
Ｃ＋ＢＣ＋ＢＣＥＦＧ加多余项( )ＢＣ
＝ＡＢ＋Ａ
－
( )Ｃ＋ＢＣ１＋ＥＦＧ
＝ＡＢ＋Ａ
－
Ｃ
二、基本法则
逻辑代数中有三个基本法则，掌握了这些法则后，可将原有的公式加以扩展或推出一些新的
公式。
１．代入法则
由于逻辑变量及函数运算结果只能取值０或１，因此逻辑等式中的任何变量或相应部分用一个变
量代替，等式仍然成立。代入法则可扩大基本的应用范围。
【例】：证明Ａ＋Ｂ＋Ｃ＝Ａ
－
·Ｂ
－
·Ｃ
－
解：Ａ＋Ｂ＝Ａ
－
×Ｂ
－
这是两变量的求反公式，若令等
Ｂ＋Ｃ＝Ｐ代入便得到
Ａ＋Ｐ＝Ａ
－
·Ｐ
－
＝Ａ
－
·Ｂ
－
·Ｃ
－
这样就得到三变量的摩根定律。
同理可将摩根定律推广到ｎ变量
Ａ１＋Ａ２＋…＋Ａｎ＝Ａ１
－
·Ａ
－
２·…·Ａ
－
ｎ
Ａ１Ａ２…Ａｎ＝Ａ１
－
＋Ａ
－
２＋…Ａ
－
ｎ
２．对偶法则
对于任何一个逻辑表达式Ｆ，如果将其中的“＋”换成“·”，“·”换成“＋”，“１”换成“０”，“０”换
—８２—
考试点（ｗｗｗ．ｋａｏｓｈｉｄｉａｎ．ｃｏｍ）名师精品课程　电话：４００－６８８５－３６５
成“１”，并保持原先的逻辑优先级，变量不变，两变量以上的非号不动，则可得原函数Ｆ的对偶式Ｇ，且
Ｆ和Ｇ互为对偶式。根据对偶法则知原式Ｆ成立，则其对偶式也一定成立。这样，我们只需记忆表３
－１基本公式的一半即可，另一半按对偶法则可求出。注意，在求对偶式时，为保持原式的逻辑优先关
系，应正确使用括号，否则就要发生错误。
如何从原式求出对偶式其过程如下：
原式
０→１
１→０
＋→×
×→＋
( )运算顺序不变 加括号
( )二变量 含二变量 以上非号不动


























变量不变
对偶式
ＡＢ＋Ａ
－
Ｃ
其对偶式为
（Ａ＋Ｂ）·（Ａ
－
＋Ｃ）
如不加括号，就变成
Ａ＋ＢＡ
－
＋Ｃ
显然是错误的。
【例】：写出ＡＢ＋Ａ
－
Ｃ＋ＢＣ＝ＡＢ＋Ａ
－
Ｃ的对偶式
解：按照上述过程其对偶式为
( )Ａ＋Ｂ Ａ
－
( ) ( ) ( )＋Ｃ Ｂ＋Ｃ ＝ Ａ＋Ｂ Ａ
－
( )＋Ｃ
３．反演法则
由原函数求反函数，称为反演或求反。摩根定律是进行反演的重要工具。多次应用摩根定律，可
以求出一个函数的反函数。
例题：Ｆ＝Ａ＋Ｂ＋Ｃ
－
＋Ｄ＋Ｅ
－
的反函数Ｆ
－
解：用摩根定律求：
Ｆ
－
＝Ａ＋Ｂ＋Ｃ
－
＋Ｄ＋Ｅ
－
＝Ａ
－
·Ｂ＋Ｃ
－
＋Ｄ＋Ｅ
－
＝Ａ
－
·Ｂ
－
·Ｃ·Ｄ＋Ｅ
－
—９２—
阎石《数字电子技术基础》考点精讲及复习思路
＝Ａ
－
·Ｂ
－
·Ｃ·Ｄ
－
·Ｅ
由上面可以看出反复用摩根定律即可，当函数较复杂时，求反过程就相当麻烦。为此，人们从实
践中归纳出求反的法则。其法则指出，将原函数Ｆ中的“·”换成“＋”，“＋”换成“·”；“０”换成“１”，
“１”换成“０”；原变量换成反变量，反变量换成原变量，长非号即两个或两个以上变量的非号不变，即
可得反函数。
反演法则的目的是能够较快的写出函数的反函数，将原式按下述过程即可求得其
原式
０→１
１→０
＋→·
·→＋
运算顺序不变
( )二变量 含二变量 以上非号不动


























变量取反
反函数
Ｆ＝Ａ＋Ｂ＋Ｃ
－
＋Ｄ＋Ｅ
－
Ｆ
－
＝Ａ
－
·Ｂ
－
·Ｃ·Ｄ
－
·Ｅ
例：求Ｆ＝ＡＢ＋Ａ
－
Ｃ的反函数
解：Ｆ
－
＝（Ａ
－
＋Ｂ
－
）（Ａ＋Ｃ
－
）＝Ａ
－
Ａ＋Ａ
－
Ｃ
－
＋ＡＢ
－
＋Ｂ
－
Ｃ
－
＝ＡＢ
－
＋Ａ
－
Ｃ
－
三、基本公式的应用
１．等式的证明
例：用公式证明Ａ
－
Ｂ＋ＡＢ
－
＝Ａ
－
Ｂ
－
＋ＡＢ
解：Ａ
－
Ｂ＋ＡＢ
－
＝Ａ
－
Ｂ
－
＋ＡＢ
－
( )求反律
＝ Ａ＋Ｂ( )
－
Ａ
－
( )＋Ｂ ( )求反律
＝ＡＡ
－
＋ＡＢ＋Ａ
－
Ｂ
－
＋Ｂ
－
Ｂ( )分配律
＝ＡＢ＋Ａ
－
Ｂ
－
( )互补律
例：证明Ａ
－
Ｂ
－
Ｃ＋Ａ
－
ＢＣ
－
＋ＡＢ
－
Ｃ
－
＋ＡＢＣ＝ＡＢＣ
证：等式左端＝Ａ
－
Ｂ
－
Ｃ＋ＢＣ( )
－
＋Ａ Ｂ
－
Ｃ
－
( )＋ＢＣ ( )分配律
＝Ａ
－
Ｂ( )Ｃ ＋ＡＢ( )Ｃ ( )异或关系
—０３—
考试点（ｗｗｗ．ｋａｏｓｈｉｄｉａｎ．ｃｏｍ）名师精品课程　电话：４００－６８８５－３６５
令ＢＣ＝Ｐ，则上式＝Ａ
－
Ｐ＋ＡＰ
－
( )代入法则
＝ＡＰ( )异或关系
＝ＡＢＣ( )证毕
２．逻辑函数不同形式的转换
逻辑函数的形式是多种多样的，一个逻辑问题可以用多种形式的逻辑函数来表示，每一种函数对
应一种逻辑电路。逻辑函数的表达形式通常可分为五种：
与或表达式
与非－与非表达式
与或非表达式
或与表达式
或非－或非表达式
例：将函数与或表达式Ｆ＝ＡＢ＋Ａ
－
Ｃ转换为其他形式
解：（１）与非———与非式。
将与或式两次取反，利用摩根定律可得
Ｆ＝ＡＢ＋Ａ
－
Ｃ＝ＡＢ·Ａ
－
Ｃ
（２）与或非式
首先求出反函数Ｆ
－
＝ＡＢ＋Ａ
－
Ｃ＝ＡＢ
－
＋Ａ
－
Ｃ
－
然后再取反一次即得与或非表达式
Ｆ＝ＡＢ
－
＋Ａ
－
Ｃ
－
（３）或与式
将与或非式用摩根定律展开，即得或与
表达式如下：
Ｆ＝ＡＢ
－
＋Ａ
－
Ｃ
－
＝ＡＢ
－
Ａ
－
Ｃ
－
＝ Ａ
－
( ) ( )＋Ｂ Ａ＋Ｃ
（４）或非———或非式
将或与表达式两次取反，用摩根定律展开
一次得或非———或非表达式
Ｆ＝ Ａ
－
( ) ( )＋Ｂ Ａ＋Ｃ ＝Ａ
－
＋Ｂ＋Ａ＋Ｃ
—１３—
阎石《数字电子技术基础》考点精讲及复习思路
四、逻辑函数的代数法化简
１．逻辑函数与逻辑图
ＡＢ＋Ａ
－
Ｂ
－
函数的逻辑图
Ｆ＝ＡＢ
－
Ｃ
－
＋ＡＢ
－
Ｃ＋ＡＢＣ
－
＋ＡＢＣ
逻辑图如左图所示，每一个与项需要一个与门，共需四个与门，最后需一个或门
经化简后，Ｆ＝Ａ，则逻辑图如上图所示，由此可见函数换件的重要性
从逻辑问题概括出来的逻辑函数式，不一定是最简式。化简电路，就是为了降低系统的成本，提
高电路的可靠性，以便用最少的门实现它们。例如函数：
Ｆ＝ＡＢＣ
－
＋ＡＢ
－
Ｃ＋Ａ
－
Ｂ＋Ｂ＋ＢＣ
如直接由该函数式得到电路图如下图所示
但如果将函数化简后其函数式为Ｆ＝ＡＣ＋Ｂ
只要两个门就够了，如下图所示。
—２３—
考试点（ｗｗｗ．ｋａｏｓｈｉｄｉａｎ．ｃｏｍ）名师精品课程　电话：４００－６８８５－３６５
２．逻辑函数化简的原则
逻辑函数化简，并没有一个严格的原则，通常遵循以下几条原则：
（１）逻辑电路所用的门最少———函数项要少
（２）各个门的输入端要少———每一项的变量数少
（３）逻辑电路所用的级数要少———速度快
（４）逻辑电路能可靠地工作
我们主要遵循（１），（２）条
（１）与或逻辑函数的化简
应用吸收定律１
ＡＢ＋ＡＢ
－
( )＝Ａ
任何两个相同变量的逻辑项，只有一个变量取值不同（一项以原变量形式出现，另一项以反变量
形式出现），我们称为逻辑相邻项（简称相邻项）。如ＡＢ与ＡＢ
－
，ＡＢＣ与ＡＢＣ都是相邻关系。如果函数
存在相邻项，可利用吸收定律１，将它们合并为一项，同时消去一个变量。
例：Ｆ＝ＡＢ＋ＣＤ＋ＡＢ
－
＋Ｃ
－
Ｄ
解：原式＝Ａ＋Ｄ
有时两个相邻并非典型形式，
应用代入法则可以扩大吸收
定律１的应用范围
例：Ｆ＝ＡＢ
－
Ｃ＋ＡＢ
－
Ｃ
－
解：令ＡＢ
－
＝Ｇ，则
Ｆ＝ＧＣ＋ＧＣ
－
＝Ｇ＝ＡＢ
－
例：Ｆ＝ＡＢＣ
－
＋ＡＢＣ
－
解：令ＢＣ
－
＝Ｇ，则
Ｆ＝ＡＧ
－
＋ＡＧ＝Ａ
例：Ｆ＝Ａ
－
Ｂ
－
Ｃ
－
＋Ａ
－
ＢＣ
－
＋ＡＢ
－
Ｃ
－
＋ＡＢＣ
－
解：原式＝Ａ
－
Ｃ
－
＋ＡＣ
－
＝Ｃ
－
利用等幂律，一项可以重复用几次
—３３—
阎石《数字电子技术基础》考点精讲及复习思路
例：Ｆ＝Ａ
－
Ｂ
－
Ｃ
－
Ｄ
－
＋Ａ
－
Ｂ
－
Ｃ
－
Ｄ＋Ａ
－
Ｂ
－
ＣＤ＋Ａ
－
ＢＣ
－
Ｄ
＋ＡＢ
－
Ｃ
－
Ｄ
其中Ａ
－
Ｂ
－
Ｃ
－
Ｄ与其余四项均是相邻关系，可以重复使用。
解：Ａ
－
Ｂ
－
Ｃ
－
Ｄ＋Ａ
－
Ｂ
－
Ｃ
－
Ｄ
－
＝Ａ
－
Ｂ
－
Ｃ
－
Ａ
－
Ｂ
－
Ｃ
－
Ｄ＋Ａ
－
ＢＣ
－
Ｄ＝Ａ
－
Ｃ
－
Ｄ
Ａ
－
Ｂ
－
Ｃ
－
Ｄ＋Ａ
－
Ｂ
－
ＣＤ＝Ａ
－
Ｂ
－
Ｄ
Ａ
－
Ｂ
－
Ｃ
－
Ｄ＋ＡＢ
－
Ｃ
－
Ｄ＝Ｂ
－
Ｃ
－
Ｄ
所以Ｆ＝Ａ
－
Ｂ
－
Ｃ
－
＋Ａ
－
Ｃ
－
Ｄ＋Ａ
－
Ｂ
－
Ｄ＋Ｂ
－
Ｃ
－
Ｄ
例：Ｆ＝ＡＢ
－
Ｃ
－
＋ＡＢ
－
Ｃ＋ＡＢＣ
－
＋ＡＢＣ
解：利用吸收律１
ＡＢ
－
Ｃ
－
＋ＡＢ
－
Ｃ＝ＡＢ
－
ＡＢＣ
－
＋ＡＢＣ＝ＡＢ
Ｆ＝ＡＢ
－
＋ＡＢ＝Ａ吸收律( )１
应用吸收定律２，吸收定律３
Ａ＋ＡＢ＝ＡＡ＋Ａ
－
( )Ｂ＝Ａ＋Ｂ
利用它们，可以消去逻辑函数式中某些多余项和多余因子。若式中存在某单因子项，则包含该因
子的其它项为多余项，可消去。如其它项包含该因子的“反”形式，则该项中的“反”因子为多余变量，
可消去。
例：Ｆ＝Ｂ
－
＋ＡＢ＋ＡＢＣＤ
解：原式＝Ｂ
－
＋ＡＢ
＝Ｂ
－
＋Ａ
例：Ｆ＝ＡＣ
－
＋ＡＢＣ
－
( )ＤＥ＋Ｆ
解：令ＡＣ
－
＝Ｇ，则
( )Ｆ＝Ｇ＋ＧＢＤＥ＋Ｆ
＝Ｇ＝ＡＣ
－
例：Ｆ＝ＡＢ
－
＋Ａ
－
Ｂ＋ＡＢＣＤ＋Ａ
－
ＢＣＤ
解：原式＝ＡＢ
－
＋Ａ
－
Ｂ＋ ＡＢ＋Ａ
－
Ｂ( )
－
ＣＤ
＝ＡＢ
－
＋Ａ
－
Ｂ＋ＡＢ
－
＋Ａ
－
ＢＣＤ
—４３—
考试点（ｗｗｗ．ｋａｏｓｈｉｄｉａｎ．ｃｏｍ）名师精品课程　电话：４００－６８８５－３６５
令ＡＢ
－
＋Ａ
－
Ｂ＝Ｇ，则
Ｆ＝Ｇ＋Ｇ
－
ＣＤ＝Ｇ＋ＣＤ
＝ＡＢ
－
＋Ａ
－
Ｂ＋ＣＤ
应用多余项定律 ＡＢ＋Ａ
－
Ｃ＋ＢＣ＝ＡＢ＋Ａ
－
( )Ｃ
例：Ｆ＝ＡＢ＋Ａ
－
ＣＤ＋ＢＣＤＥ
解：原式＝ＡＢ＋ＡＣＤ
例：Ｆ＝ＡＢＣ
－
＋ Ａ
－
( )＋ＣＤ＋ＢＤ
解：原式＝ＡＢＣ
－
＋ＡＣ
－
Ｄ＋ＢＤ
＝ＡＢＣ＋ＡＣ
－
Ｄ
例：化简Ｆ＝ＡＣ＋Ａ
－
Ｄ＋Ｂ
－
Ｄ＋ＢＣ
－
解：原式＝ＡＣ＋ＢＣ
－
＋ Ａ
－
＋Ｂ( )
－
Ｄ
＝ＡＣ＋ＢＣ
－
＋ＡＢＤ＋ＡＢ
＝ＡＣ＋ＢＣ
－
＋Ｄ＋ＡＢ
＝ＡＣ＋ＢＣ
－
＋Ｄ
添项法
在函数中加入零项因子ｘ·ｘ
－
或ｘ·ｘ
－
ｆＡＢ( )… ，利用加进的新项，进一步化简函数。
例：化简Ｆ＝ＡＢＣ
－
＋ＡＢＣ·ＡＢ
解：原式＝ＡＢＡＢ＋ＡＢＣ
－
＋ＡＢＣ·ＡＢ
＝ＡＢＡＢ＋Ｃ( )
－
＋ＡＢＣ·ＡＢ
＝ＡＢＡＢＣ＋ＡＢＣ·ＡＢ
＝ＡＢＣ
综合例子
例：化简Ｆ＝ＡＤ＋ＡＤ
－
＋ＡＢ＋Ａ
－
Ｃ＋ＢＤ＋ＡＣＥＧ＋Ｂ
－
ＥＧ＋ＤＥＧＨ
解：原式＝Ａ＋ＡＢ＋Ａ
－
Ｃ＋ＢＤ＋ＡＣＥＧ＋Ｂ
－
ＥＧ＋ＤＥＧＨ
ＡＢ＋ＡＢ
－
( )＝Ａ
＝Ａ＋Ａ
－
Ｃ＋ＢＤ＋Ｂ
－
( )ＥＧ＋ＤＥＧＨ Ａ＋ＡＢ＝Ａ
—５３—
阎石《数字电子技术基础》考点精讲及复习思路
＝Ａ＋Ｃ＋ＢＤ＋Ｂ
－
ＥＧ＋ＤＥＧＨ Ａ＋Ａ
－
( )Ｂ＝Ａ＋Ｂ
＝Ａ＋Ｃ＋ＢＤ＋Ｂ
－
ＥＧ( )多余项定律
例：Ｆ＝ＡＢ
－
＋ＢＣ
－
＋Ｂ
－
Ｃ＋Ａ
－
Ｂ
此题按照常规的方法用公式无法再化简，经过一定的处理可再化简：
解：Ｆ＝ＡＢ
－
＋ＢＣ
－
＋Ｂ
－
ＣＡ＋Ａ( )
－
＋Ａ
－
ＢＣ＋Ｃ( )
－
互补律Ａ
－
( )＋Ａ＝１
＝ＡＢ
－
＋ＢＣ
－
＋ＡＢ
－
Ｃ＋ＡＢＣ＋Ａ
－
ＢＣ
－
＋ＡＢＣ( )分配律
ＡＢ
－
＋ＡＢ
－
Ｃ＝ＡＢ
－
＝ＡＢ
－
＋ＢＣ
－
＋Ａ
－
Ｂ
－
Ｃ＋Ａ
－
ＢＣ
－
＋Ａ
－
ＢＣ
ＢＣ
－
＋Ａ
－
ＢＣ
－
＝ＢＣ( )
－
＝ＡＢ
－
＋ＢＣ
－
＋Ａ
－
Ｂ
－
Ｃ＋Ａ
－
ＢＣ
＝ＡＢ
－
＋ＢＣ
－
＋Ａ
－
ＣＡ
－
Ｂ
－
Ｃ＋Ａ
－
ＢＣ＝Ａ
－
( )Ｃ
例：Ｆ＝Ａ
－
Ｃ＋Ｂ
－
Ｃ＋ＡＢ
解法( )１：加多余项
Ｆ＝Ａ
－
Ｃ＋Ｂ
－
Ｃ＋ＡＢ＋ＡＣＢ
－
Ｃ，ＡＢ多余项为( )ＡＣ
＝Ｃ＋Ｂ
－
Ｃ＋ＡＢＡＣ＋Ａ
－
Ｃ＝Ｃ吸收律( )１
＝Ｃ＋ＡＢ吸收律( )２
解法( )２：Ｆ＝ Ａ
－
＋Ｂ( )
－
Ｃ＋ＡＢ( )分配律
＝ＡＢＣ＋ＡＢ( )求反律
＝Ｃ＋ＡＢ
【华侨大学２０１２年】
用代数法将逻辑函数化简为最简的与或表达式，并画出仅用两输入与非门实现的逻辑图。（１５
分）
Ｌ＝（Ｂ
－
Ｃ＋ＢＤ
－
＋ＢＤ）（Ａ
－
＋ＡＢ
－
＋Ｂ）ＡＣ
解：
—６３—
考试点（ｗｗｗ．ｋａｏｓｈｉｄｉａｎ．ｃｏｍ）名师精品课程　电话：４００－６８８５－３６５
Ｌ＝Ａ
－
Ｃ＋ＢＣ
－
＝Ａ
－
Ｃ＋ＢＣ
－
＝Ａ
－
ＣＢＣ
－
【北京科技大学２０１２年】
（本题８分）已知Ａ、Ｂ是输入，Ｘ是输出，下列波形所表明的函数关系是什么？分别用真值表、最
简表达式和最简电路表示之。
解：
真值表
Ａ Ｂ Ｘ
０ ０ １
０ １ １
１ ０ １
１ １ ０
函数表达式
Ｘ＝Ａ
－
Ｂ
－
最简电路
通过以上各例可看出代数法化简在使用中存在如下问题：
１．逻辑代数与普通代数的公式易混淆，化简过程要求对所有公式熟练掌握。
———需记大量的公式
２．代数法化简无一套完善的方法可循，它依赖于人的经验和灵活性。 ———无统一模式
３．用这种化简方法技巧强，较难掌握。特别是对代数化简后得到的逻辑表达式是否是最简式判
断有一定困难。
———需要一定的技巧
４．难于判断结果是否最简。为此出现一种既简便又直观的化简方法—图形法化简，即卡诺图化
简法。
—７３—
阎石《数字电子技术基础》考点精讲及复习思路
第５讲　逻辑代数与
逻辑函数化简（２）
五、卡诺图化简
卡诺图化简的依据是吸收律１，即二项逻辑相邻项可合并为一项，保留共有的变量，消去表现形式
不同的变量 ＡＢ＋ＡＢ
－
( )＝Ａ。所谓逻辑相邻项，即含有相同变量，其中只有一个变量表现形式不同的
逻辑项。因此，如已知一个逻辑函数的相邻关系，可以反复应用其吸收定律１即可。
Ｆ＝Ａ
－
Ｂ
－
Ｃ
－
＋Ａ
－
Ｂ
－{ Ｃ
Ａ
－
Ｂ
－
＋Ａ
－
ＢＣ
－
＋Ａ{ －
Ａ
－
Ｂ
{ＢＣ＋ＡＢＣ
ＢＣ
＝Ａ
－
Ｂ
－
＋Ａ
－{ Ｂ
Ａ
－
＋ＢＣ
＝Ａ
－
＋ＢＣ
但是有的逻辑函数相邻关系不直观，如：
Ｆ＝Ａ
－
Ｂ
－
ＣＤ＋ＡＢＣ＋Ｂ
－
Ｃ
－
＋ＢＣＤ
各项变量不相同，找不出相邻关系。为了寻找逻辑相邻关系，提出逻辑函数的标准式。
１．逻辑函数的标准式———最小项标准式
最小项标准式是以“与或”形式出现的标准式。
最小项—含有逻辑函数的全部变量的与项。每个变量只能以原反变量出现一次。且在一个与项
中，对应一种输入组合使Ｆ＝１。全由最小项相或组成的逻辑函数称为最小项标准式。
为表示方便，将最小项进行编号ｍｉ其下标与二进制数一致。
以三变量为例
ＡＢＣ 最小项函数项 编号
０００ Ａ
－
Ｂ
－
Ｃ
－ ｍ０
—８３—
考试点（ｗｗｗ．ｋａｏｓｈｉｄｉａｎ．ｃｏｍ）名师精品课程　电话：４００－６８８５－３６５
ＡＢＣ 最小项函数项 编号
００１ Ａ
－
Ｂ
－
Ｃ ｍ１
０１０ Ａ
－
ＢＣ
－ ｍ２
０１１ Ａ
－
ＢＣ ｍ３
１００ ＡＢ
－
Ｃ
－ ｍ４
１０１ ＡＢ
－
Ｃ ｍ５
１１０ ＡＢＣ
－ ｍ６
１１１ ＡＢＣ ｍ７
这样函数表达式：
Ｆ＝Ａ
－
Ｂ
－
Ｃ
－
＋Ａ
－
Ｂ
－
Ｃ＋Ａ
－
ＢＣ
－
＋Ａ
－
ＢＣ＋ＡＢＣ
就可以写成：
＝ｍ０＋ｍ１＋ｍ２＋ｍ３＋ｍ７
＝Σ０，１，２，３，( )７
一个变量Ａ有二个最小项：
２( )１ Ａ，Ａ
－
二个变量ＡＢ有四个最小项：
２( )２ Ａ
－
Ｂ
－
，Ａ
－
Ｂ，ＡＢ
－
，ＡＢ
三个变量ＡＢＣ有八个最小项：
２( )３ Ａ
－
Ｂ
－
Ｃ
－
，Ａ
－
Ｂ
－
Ｃ，Ａ
－
ＢＣ
－
，Ａ
－
ＢＣ，ＡＢ
－
Ｃ
－
，ＡＢ
－
Ｃ，ＡＢＣ
－
，ＡＢＣ
以此类推，四个变量ＡＢＣＤ共有２４＝１６个最小项，ｎ变量共有２ｎ个最小项
最小项标准式：全是由最小项组成的“与或”式，便是最小项标准式（不一定由全部最小项组成）。
例如：
Ｆ＝Ａ
－
ＢＣ
－
＋Ａ
－
ＢＣ＋ＡＢ
－
Ｃ
－
＋ＡＢ
－
Ｃ＋ＡＢＣ
＝∑ ２，３，４，５，( )７
２．如何由一般式获得最小标准式
（１）代数法。对逻辑函数的一般式采用添项法，例如：
Ｆ＝Ａ
－
Ｂ
－
Ｃ
－
＋ＢＣ＋ＡＣ
－
由上式可看出，第二项缺少变量Ａ，第三项缺少变量Ｂ，我们可以分别用 Ａ＋Ａ( )
－
和 Ｂ＋Ｂ( )
－
乘第二
项和第三项，其逻辑功能不变。
—９３—
阎石《数字电子技术基础》考点精讲及复习思路
Ｆ＝Ａ
－
Ｂ
－
Ｃ
－
＋ＢＣＡ＋Ａ( )
－
＋ＡＣ
－
Ｂ＋Ｂ( )
－
＝Ａ
－
Ｂ
－
Ｃ
－
＋ＡＢＣ＋Ａ
－
ＢＣ＋ＡＢＣ
－
＋ＡＢ
－
Ｃ
－
＝ｍ０＋ｍ３＋ｍ４＋ｍ６＋ｍ７
＝∑ ０，３，４，６，( )７
（２）真值表法。将原逻辑函数Ａ、Ｂ、Ｃ取不同值组合起来，得其真值表，而该逻辑函数是将 Ｆ＝１
那些输入变量相或而成的
某逻辑函数的真值表
ＡＢＣ Ａ
－
Ｂ
－
Ｃ
－ ＢＣ ＡＣ
－ Ｆ
０００ １ ０ ０ １
００１ ０ ０ ０ ０
０１０ ０ ０ ０ ０
０１１ ０ １ ０ １
１００ ０ ０ １ １
１０１ ０ ０ ０ ０
１１０ ０ ０ １ １
１１１ ０ １ ０ １
从真值表上得到
Ｆ＝Ａ
－
Ｂ
－
Ｃ
－
＋Ａ
－
ＢＣ＋ＡＢ
－
Ｃ
－
＋ＡＢＣ
－
＋ＡＢＣ
＝∑ ０，３，４，６，( )７
与代数法所得结论一致
Ｆ＝Ａ
－
Ｂ
－
Ｃ
－
＋Ａ
－
ＢＣ＋ＡＢ
－
Ｃ
－
＋ＡＢＣ
－
＋ＡＢＣ
＝∑ ０，３，４，６，( )７
３．最小项的性质
（１）对任何变量的函数式来讲，全部最小项之和为１，即：
∑
２ｎ－１
ｉ＝０
ｍｉ＝１
（２）两个不同最小项之积为０，即：
ｍｉ·ｍｊ＝０　 ｉ≠( )ｊ
（３）ｎ变量有２ｎ项最小项，且对每一最小项而言，有ｎ个最小项与之相邻。
有了最小项标准式，但要较快找出其全部相邻关系，并确定相邻项如何合并，使之结果最简，仍然
—０４—
考试点（ｗｗｗ．ｋａｏｓｈｉｄｉａｎ．ｃｏｍ）名师精品课程　电话：４００－６８８５－３６５
十分困难。
为此用图形将最小项巧妙地排列，使逻辑相邻与几何位置相邻一一对应，这样逻辑相邻关系就一
目了然。
４．卡诺图的结构
卡诺图的结构特点是需保证逻辑函数的逻辑相邻关系，即图上的几何相邻关系。卡诺图上每一
个小方格代表一个最小项。为保证上述相邻关系，每相邻方格的变量组合之间只允许一个变量取值
不同。为此，卡诺图的变量标注均采用循环码。
一变量卡诺图：有２１＝２个最小项，因此有两个方格。外标的０表示取Ａ的反变量，１表示取Ａ的
原变量。其图如下图所示。
二变量卡诺图：有２２＝４个最小项，因此有四个方格。外标的０、１含义与前一样。其图如下图
所示。
三变量卡诺图：有２３＝８个最小项，其卡诺图如下图所示。
四变量卡诺图：有２４＝１６个最小项，其卡诺图如左图所示。
—１４—
阎石《数字电子技术基础》考点精讲及复习思路
需要指出的是，一个平面只能完整反映二变量的相邻关系。多于二变量的逻辑相邻关系，除了几
何位置相邻外，还应加上对折重叠相邻。如四变量，ｍ５从几何位置上其相邻项有 ｍ１、ｍ４、ｍ７和 ｍ１３；而
ｍ８从几何位置上只有ｍ１２，ｍ９与之相邻，另二个相邻项通过对折重叠项找出，以 ａａ线对折重叠项是
ｍ０；以ｂｂ线对折重叠项是ｍ１０。故ｍ８的逻辑相邻项为ｍ０、ｍ９、ｍ１０、ｍ１２。
五变量卡诺图：有２５＝３２个最小项，其卡诺图如下图所示。
５．逻辑函数的卡诺图表示法
逻辑函数的真值表与卡诺图有一一对应的关系，卡诺图中的每一方格对应真值表中的一项。给
出函数的最小项标准式。在卡诺图中，对号入座
( )ＦＡＢＣ ＝∑ ０，２，３，５，( )７
例：
函数中含有的最小项填“１”，没含有的最小项填０，也可不填。
Ｆ＝ＡＢＣ＋ＡＢＣ
－
＋ＡＢ
－
Ｃ＋Ａ
－
Ｂ
－
Ｃ＝ｍ７＋ｍ６＋ｍ５＋ｍ１
如给出的是一般表达式。则逐项填入卡诺图
例：Ｆ＝Ａ
－
ＢＣ＋ＢＣＤ＋Ａ
－
ＣＤ＋ＡＢＤ
－
卡诺图
Ａ
－
ＢＣ→ｍ６、ｍ７
—２４—
考试点（ｗｗｗ．ｋａｏｓｈｉｄｉａｎ．ｃｏｍ）名师精品课程　电话：４００－６８８５－３６５
ＢＣＤ→ｍ７、ｍ１５
Ａ
－
ＣＤ→ｍ３、ｍ７
ＡＢＤ
－
→ｍ１２、ｍ１４
６．最小项合并规律
（１）两相邻项可合并为一项，消去一个取值不同的变量，保留相同变量；（标注为１→原变量，０→
反变量；）
（２）四相邻项可合并为一项，消去两个取值不同的变量，保留相同变量，（标注为１→原变量，０→
反变量；）
（３）八相邻项可合并为一项，消去三个取值不同的变量，保留相同变量，（标注与变量关系同上。）
①二个相邻项可合并为一项，消去一个取值不同的变量，保留相同变量。如图所示
②四个相邻项可合并为一项，消去二个取值不同的变量，保留相同的变量，如图所示。
③八个相邻项可合并为一项，消去三个取值不同的变量，保留相同的变量，如图所示。
按上规律，不难得１６个相邻项合并的规律。这里需要指出的是：合并的规律是２ｎ个最小项的相
—３４—
阎石《数字电子技术基础》考点精讲及复习思路
邻项可合并，不满足２ｎ关系的最小项不可合并。如２、４、８、１６个相邻项可合并，其它的均不能合并，而
且相邻关系应是封闭的，如ｍ０、ｍ１、ｍ３、ｍ２四个最小项，ｍ０与ｍ１，ｍ１与 ｍ３，ｍ３与 ｍ２均相邻，且 ｍ２和 ｍ０
还相邻。这样的２ｎ个相邻的最小项可合并。而ｍ０、ｍ１、ｍ３、ｍ７，由于ｍ０与ｍ７不相邻，因而这四个最小
项不可合并为一项。
７．用卡诺图化简“与或式”
步骤如下：
１）将函数用卡诺图表示。
２）用最少的卡诺圈圈全部“１”方格，每一个卡诺圈对应一个与项，卡诺圈最少即与项最少，逻辑电
路最简。
３）在最少的卡诺圈的前提下，尽可能圈大圈。变量数最少。
４）不要圈多余圈。（其图“１”方格均被别的卡诺圈圈过。）
５）将上述全部卡诺圈结果相“或”，即得化简后的新函数。
６）由逻辑门组成逻辑电路
例：化简Ｆ＝Ｂ
－
ＣＤ＋ＢＣ
－
＋Ａ
－
Ｃ
－
Ｄ＋ＡＢ
－
Ｃ
解：第一步：用卡诺图表示该逻辑函数。
Ｂ
－
ＣＤ对应ｍ３、ｍ１１
ＢＣ
－
对应ｍ４、ｍ５、ｍ１２、ｍ１３
—４４—
考试点（ｗｗｗ．ｋａｏｓｈｉｄｉａｎ．ｃｏｍ）名师精品课程　电话：４００－６８８５－３６５
采用恒流源电路后，各支路权电流的大小均不受模拟开关导通电阻和压降的影响，这样就降低了
对模拟开关的要求，提高了转换精度。
【例１】：已知８位ＤＡＣ转换器的基准电压ＵＲＥＦ＝－１２Ｖ（１）：输入二进制数为０００００００１，输出模拟
电压ｕｏ是
多少？
（２）输入二进制数为１１１１１１１１，输出模拟电压ｕｏ是多少？
（３）该电路的分辨率是多少？
解：１：ｕｏ＝ＵＬＳＢ＝ＵＲＥＦ／２
ｎ×１＝１２／２５６≈０．０４７Ｖ
２：ｕｏ＝Ｕｍ＝（ＵＲＥＦ／２
ｎ）×（２ｎ－１）＝（１２／２５６）×２５５≈１１．９５Ｖ
３：Ｄ＝ＵＬＳＢ／Ｕｍ＝０．０４７／１１．９５≈０．００３９＝０．３９％
或Ｄ＝１／（２ｎ－１）＝１／２５５≈０．００３９＝０．３９％
【例２】：三位ＤＡＣ，当输入数字量由１０１变为１１１，其输出的增量△ｕｏ＝１Ｖ。求：
１）分辨率Ｄ；
２）基准电压ＵＲＥＦ＝？
３）最大输出电压Ｕｍ？
解：１）Ｄ＝１／（２ｎ－１）＝１／７
２）ＵＬＳＢ是输入数字量变化最小单位的输出电压，
因为１０１变为１１１，数字量变化为两个最小单位，
所以ＵＬＳＢ＝（１／２）×△ｕｏ＝０．５Ｖ
又ＵＬＳＢ＝－（ＵＲＥＦ／２
ｎ）×１
∴ＵＲ＝－ＵＬＳＢ×２
ｎ＝－４Ｖ
３）Ｄ＝ＵＬＳＢ／ＵｍＵｍ＝ＵＬＳＢ／Ｄ＝３．５Ｖ
或Ｕｍ＝－（ＵＲＥＦ／２
ｎ）×（２ｎ－１）＝３．５Ｖ
【北京邮电大学２００１年考研题】
数／模转换器电路如图，ｄ０、ｄ１、ｄ２、ｄ３为数字量，Ｓ０、Ｓ１、Ｓ２、Ｓ３为模拟开关，当 ｄｉ＝０，开关接地，为
“１”时接运算放大器的输入端。已知转换输出的模拟电压ＶＯ的最大值为７．５Ｖ。试求：
ａ）参考电压ＶＲＥＦ的值。
ｂ）当ｄ３ｄ２ｄ１ｄ０＝１０１０时，ＶＯ＝？
—１９１—
阎石《数字电子技术基础》考点精讲及复习思路
解：根据ＶＯ＝－
ＶＲＥＦ
２ｎ
∑
ｎ－１
ｉ＝０
Ｂｉ２
ｉ
ａ）当输入最大是数字量为１１１１＝１５，２４＝１６，代入上式
７．５＝
ＶＲＥＦ
１６１５　ＶＲＥＦ＝７．５
１６
１５＝８Ｖ
ｂ）当输如数字量为１０１０＝１０，代入上式
ＶＯ＝
８
１６１０＝５Ｖ
【北京邮电大学２００１年考研题】
某模／数转换器的输入为０—１０Ｖ的模拟电压，输出为８位二进制数字信号 Ｄ７—Ｄ０，该模／数转换
器能分辨的最小电压应为多少？
【华南理工大学考研题】
某十位ＤＡＣ在输入为０００１１０００１０时输出为０．１６Ｖ，求当输入为０１１０００１０００时的输出电压。
解：ＶＯ＝－
ＶＲＥＦ
２ｎ
∑
ｎ－１
ｉ＝０
Ｂｉ２
ｉ－
ＶＲＥＦ
２ｎ
＝０．１６９８
ＶＯ＝
０．１６
９８ ×３９２＝０．６４
—２９１—
考试点（ｗｗｗ．ｋａｏｓｈｉｄｉａｎ．ｃｏｍ）名师精品课程　电话：４００－６８８５－３６５
第２３讲　模数转换器
一、ＡＤＣ的组成
１．ＡＤＣ的两个组成部分及其作用
（１）采样保持电路
采样开关Ｓ的控制信号ＣＰｓ的频率ｆｓ必须满足公式
ｆｓ≥２ｆｍａｘ
（ｆｉｍａｘ为输入电压频谱中的最高频率），即其周期Ｔｓ很小，而且采样时间τ比Ｔｓ更要小许多倍，这样
就能将采样保持后的ｕＩ′（ｔ）不失真地恢复成输入电压ｕＩ（ｔ）。该公式称为采样定理。
（２）量化编码电路
—３９１—
阎石《数字电子技术基础》考点精讲及复习思路
采样保持电路的输出信号ｕＩ′（ｔ）虽已成为阶梯状，但其阶梯幅值仍是连续可变的，有无限多个数
值，无法与ｎ位有限的２ｎ个数字量输出Ｘ相对应。因此，必须将采样后的值只限于在某些规定个数的
离散的电平上，凡介于两个离散电平之间的采样值，就要用某种方式整理归并到这两个离散电平之一
上。这种将幅值取整归并的方式及过程称为“量化”。
将量化后的有限个整量值用ｎ位一组的某种数字代码（如二进制码、ＢＣＤ码或Ｇｒａｙ码等）对应描
述以形成数字量，这种用数字代码表示量化幅值的过程称作“编码”。
２．量化方式和量化误差
（１）只舍不入法。当输入ｕＩ在某两个相邻的量化值之间，即（ｋ－１）·ｓ$ｕ１＜ｋ·ｓ（ｋ为整数）
（２）四舍五入法。当ｕＩ的尾数不足
ｓ
２时，用舍尾取整法得其量化值；当ｕＩ的尾数等于或大于
ｓ
２时，
则入整。
例如：已知ｓ＝１Ｖ，则ｕＩ＝２．１Ｖ时，ｕＩ＝２Ｖ；ｕＩ＝２．７Ｖ时ｕＩ ＝３Ｖ。
二、模数转换电路通常可分为两大类
１．间接法：
将采样保持的模拟信号，首先转换成与模拟量成正比的时间Ｔ或频率Ｆ，然后再将中间量Ｔ、Ｆ转
换成数字量。由于通常用频率恒定的时钟脉冲通过计数器来转换，因此也称计数式。
特点是：速度低、精度高、抑制干扰能力较强
典型电路：双积分型Ａ／Ｄ转换器
电压频率转换型Ａ／Ｄ转换器
２．直接法：
通过与一套基准电压采样保持信号进行比较，从而直接转换成数字量。
特点：速度快
转换精度易得到保证
电路采用数字电路构成，故调整方便
典型电路：
逐次逼近型Ａ／Ｄ转换器
并型比较型Ａ／Ｄ转换器
—４９１—
考试点（ｗｗｗ．ｋａｏｓｈｉｄｉａｎ．ｃｏｍ）名师精品课程　电话：４００－６８８５－３６５
三、双积分ＡＤＣ
双积分ＡＤＣ又称双斜率ＡＤＣ，是间接法的一种，它先将模拟电压 ｕＩ转换成与之大小对应的时间
Ｔ，再在时间间隔Ｔ内用计数器对固定频率计数，计数器所计的数字量就正比于输入模拟电压。
主要组成：
１）积分器。由运算放大器Ａ１和ＲＣ积分网络组成。它是转换器的核心。其开关Ｓ受触发器Ｆｎ控
制。
Ｑｎ＝０，Ｓ接输入电压ｕｉ，积分器对ｕｉ积分；
Ｑｎ＝１，Ｓ接基准电压－ＵＲ，积分器对－ＵＲ积分。
其输出ｕＡ接过零比较器Ａ２。
２）过零比较器。ＵＡ＞０　比较器输出ＵＣ＝０
ＵＡ＜（＝）０　比较器输出ＵＣ＝１
其输出ＵＣ接时钟控制门Ｇ。
—５９１—
阎石《数字电子技术基础》考点精讲及复习思路
３）时钟控制门Ｇ。ＵＣ＝１，Ｇ门打开，基准时钟通过计数器对其计数；
ＵＣ＝０，Ｇ门被封闭，计数器停止计数。
３）计数器和定时电路。
由ｎ＋１个触发器组成，Ｆ０…Ｆｎ－１组成ｎ位二进制计数器。
在启动脉冲作用下，全部ＦＦ置０Ｑｎ＝０，积分器对ｕｉ积分，ｕＡ＜０，故ＵＣ＞０，Ｇ门开启，ｎ位二进制
计数器计数，当计数器计到第２ｎ个时钟后Ｑ０到Ｑｎ－１为全“１”态返回到全“０”，向 Ｑｎ进位使 Ｑｎ＝１，发
出定时控制信号。
积分器对－ＵＲ反相积分。此时ＵＣ仍为１，计数器再次从０开始计数，直到积分器输出 ｕＡ＞０，使
ＵＣ＝０，Ｇ门关闭，此时，计数器所计二进制数即为与输入模拟采样保持信号的平均值成正比的数
字量。
（１）采样阶段：
在启动脉冲作用下，将全部触发器置０。由于 Ｑｎ＝０，使开关 Ｓ与输入信号 ｕＩ连接，Ａ／Ｄ转换开
始。ｕＩ加至积分器的输入端后，积分器对ｕＩ进行积分，输出为
ｕＡ＝－
１
τ∫
ｔ
０ｕ１ｄｔ
式中，τ＝ＲＣ，为积分时间常数。
由于ｕＡ＜０，过零比较器输出ＵＣ＝１，Ｇ门打开，ｎ位二进制计数器从０开始计数，一直到
—６９１—
考试点（ｗｗｗ．ｋａｏｓｈｉｄｉａｎ．ｃｏｍ）名师精品课程　电话：４００－６８８５－３６５
ｔ＝Ｔ１＝２
ｎＴＣＰ
ｕＡ＝ＵＡ０＝－
Ｔ１
τ
ｕＩ＝－
２ｎＴＣＰ
τ
ｕＩ
触发器Ｆ０～Ｆｎ－１又全部回到０，而触发器Ｆｎ由０翻至１，Ｑｎ＝１，开关Ｓ转接至基准电源－ＵＲ，采样
阶段结束。此时
ｕＡ＝ＵＡ０＝－
Ｔ１
τ
ｕＩ＝－
２ｎＴＣＰ
τ
ｕＩ
（２）比较阶段：开关Ｓ转接至基准电源
#
ＵＲ后，积分器对－ＵＲ进行积分，积分器输出
ｕＡ＝ＵＡ０－
１
τ∫
ｔ
Ｔ１（－ＵＲ）ｄｔ＝－
２ｎＴＣＰ
τ
ｕ１＋
ＵＲ
τ
（ｔ－Ｔ１）
当ｕＡ≥０时，过零比较器输出ＵＣ＝０，Ｇ门被封锁，计数器停止计数。假设此时计数器已记录了Ｎ
个脉冲，则
Ｔ２＝ｔ－Ｔ１＝ＮＴＣＰ
代入上式得
ｕＡ＝－
２ｎＴＣＰ
τ
ｕ１＋
ＵＲ
τ
ＮＴＣＰ＝０
求得Ｎ＝２
ｎ
ＵＲ
ｕＩ
ＵＩ较小ＵＡＯ第低。Ｔ２短
ＵＩ较大ＵＡＯ第高。Ｔ２长
—７９１—
阎石《数字电子技术基础》考点精讲及复习思路
由此式可见：计数器所计脉冲数Ｎ与输入电压ｕｉ成正比，Ｎ所对应的二进制代码即为输出的数字
量。实现ＡＤＣ。该ＡＤＣ：抗干扰能力强。但转换时间长。一般用在对速度要求不高的仪器仪表中。
２．逐次逼近式ＡＤＣ
四位逐次逼近型Ａ／Ｄ转换器原理框图
逐次逼近型Ａ／Ｄ转换器是采用较多的一种。他的转换过用天平称物种相似。从最重的砝码开
始放，与被称物体进行比较，若物体重于砝码，则该砝码保留，否则移去。再加第二个次重砝码……照
此进行下去，一直到加到最小一个砝码。将全部留下的砝码重量相加，就是物体重量。逐次逼近型
Ａ／Ｄ转换器，就是将输入模拟信号与不同的参考电压做多次比较，使转换所得得数字量在数值上逐次
逼近输入模拟量。
举例说明如下：
四位逐次逼近型Ａ／Ｄ电路，ＵＲＥＦ＝８Ｖ，输入模拟ｕｉ＝６．３Ｖ。
工作过程如下
首先高位为１，及数字量为
１０００→（８／１６）×８＝４Ｖ＜６．３Ｖ　　故该位的１保留
１１００→（１２／１６）×８＝６Ｖ＜６．３Ｖ　　故该位的１保留
１１１０→（１４／１６）×８＝７Ｖ＞６．３Ｖ　　故该位的１移去
—８９１—
考试点（ｗｗｗ．ｋａｏｓｈｉｄｉａｎ．ｃｏｍ）名师精品课程　电话：４００－６８８５－３６５
１１０１→（１３／１６）×８＝６．５Ｖ＞６．３　　故该位的１移去
与全部参考电压比较结束得
６．３Ｖ→１１００
如用８位逐次逼近型Ａ／Ｄ转换器，过程如下
１０００００００→（１２８／２５６）×８＝１２８／３２＝４Ｖ＜６．３Ｖ　　保留该位
１１００００００→（１９２／２５６）×８＝１９２／３２＝６Ｖ＜６．３Ｖ　　保留该位
１１１０００００→（２２４／２５６）×８＝２２４／３２＝７Ｖ＞６．３Ｖ　　移去该位
１１０１００００→（２０８／２５６）×８＝２０８／３２＝６．５ｖ＞６．３Ｖ　　移去该位
１１００１０００→（２００／２５６）×８＝２００／３２＝６．２５Ｖ＜６．３Ｖ　　保留该位
１１００１１００→（２０４／２５６）×８＝２０４／３２＝６．３７５Ｖ＞６．３Ｖ　　移去该位
１１００１０１０→（２０２／２５６）×８＝２０２／３２＝６．３１２５Ｖ＞６．３Ｖ　　移去该位
１１００１００１→（２０１／２５６）×８＝２０１／３２＝６．２８１２５Ｖ＜６．３Ｖ　　保留该位
比较结束
６．３Ｖ→１１００１００１
由上面的例子可看出
１位数越多精度越高
２位数越多转换时间越长
转换时间Ｔ＝（ｎ＋１）Ｔｃｐ
ｎ是逐次逼近型Ａ／Ｄ转换器的位数Ｔｃｐ是时钟信号的周期
３．并行比较型电路
输入模拟电压的范围ｕＩ＝０～８Ｖ，ｕＩｍ＝８Ｖ；输出三位二进制代码（ｎ＝３）。采用四舍五入的量化方
式，量化间隔ｓ＝
２ｕＩｍ
２ｎ＋１－１
＝２１５ｕＩｍ＝
１６
１５Ｖ量化标尺是用电阻分压器形成
１
１５ＵＲ，＝
３
１５ＵＲ，…，
１３
１５ＵＲ各分度
值的，并作为各比较器Ｃ１～Ｃ７的比较参考电平。因采用四舍五入法量化，第一个比较器的参考电平应
取
ｓ
２＝
１
１５·ＵＲ＝
８
１５Ｖ。采样保持后的输入电压ｕＩ与这些分度值相比较，当 ｕＩ大于比较参考电平时，比
—９９１—
阎石《数字电子技术基础》考点精讲及复习思路
较器输出１电平，反之输出０电平，从而各比较器输出电平的状态就与输入电压量化后的值相对应。
各比较器输出并行送至由Ｄ触发器构成的寄存器内，再经过编码电路将比较器的输出转换成三位二
进制代码ｘ２ｘ１ｘ０。输入电压与代码的对应关系如表８－２所示。
四、ＡＤＣ的主要技术指标
１．分辨率
分辨率指ＡＤＣ对输入模拟信号的分辨能力。从理论上讲，一个ｎ位二进制数输出ＡＤＣ应能区分
输入模拟电压的２ｎ个不同量级，能区分输入模拟电压的最小值为满量程输入的１／２ｎ。在最大输入电
压一定时，输出位数愈多，量化单位愈小，分辨率愈高。例如，ＡＤＣ输出为八位二进制数，输入信号最
大值为５Ｖ，其分辨率为
分辨率＝
Ｕｍ
２８
＝５２５６＝１９．５３ｍＶ
２．转换误差
转换误差通常是以输出误差的最大值形式给出。它表示 ＡＤＣ实际输出的数字量和理论上的输
出数字量之间的差别，常用最低有效位的倍数表示。如给出相对误差小于等于 ±ＬＳＢ／２，这就表明实
际输出的数字量和理论上应得到的输出数字量之间的误差小于最低位的半个字。
３．转换速度
转换时间是指ＡＤＣ从转换信号到来开始，到输出端
得到稳定的数字信号所经过的时间。此时间与转换电路
的类型有关。不同类型的转换器，其转换速度相差很大。并行 ＡＤＣ转换速度最高，八位二进制
输出的单片ＡＤＣ其转换时间在５０ｎｓ内，逐次逼近型ＡＤＣ转换速度次之，一般在１０～５０μｓ，也有的可
达数百纳秒。双积分式ＡＤＣ转换速度最慢，其转换时间约在几十毫秒至几百毫秒间。实际应用中，
应从系统总的位数、精度要求、输入模拟信号的范围及输入信号极性等方面综合考虑ＡＤＣ的选用。
—００２—
考试点（ｗｗｗ．ｋａｏｓｈｉｄｉａｎ．ｃｏｍ）名师精品课程　电话：４００－６８８５－３６５