概要信息：

　目　　录　
第一章　矢量分析与场论 （１）
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
第二章　静电场 （３）
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
第三章　恒定电流的电场 （９）
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
第四章　恒定磁场 （１０）
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
第五章　静态场的解 （１５）
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
第六章　时变电磁场 （２０）
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
第七章　均匀平面电磁波 （２４）
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
第八章　导行电磁波 （３２）
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
第九章　电磁辐射 （３３）
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
【注】　为了使讲义与视频内容相对应，故讲义中题目的序号非顺序，给您带来的不便，敬请谅解。
第一章　矢量分析与场论
一、重点内容
矢量分析与场论是研究许多科学问题的一种有用工具。
场论是讨论物理量在特定区域内分布、变化规律的理论，给出描述场问题的统一方法和理论。
·数量场的等值面、方向导数和梯度的概念、物理意义；
·矢量场的矢量线、通量、散度、环量及旋度的概念、物理意义；
·亥姆霍兹定理。
二、真题及典型题解析
１．填空题
（１）在自由空间中，一个孤立的点电荷，其产生的等电位面是 。（２分，南京理工大学
２０１１年）
（２）标量场φ＝ｘ２ｙｚ位于点（２，３，１）处的等值面法线方向单位矢量是 。（３分，华中科技
大学２００６年）
（３）已知电位函数Φ＝ｅ－ｙｃｏｓｘ，则电场强度Ｅ
→
＝ 。（２分，南京理工大学２０１１年）
（４）矢量函数 Ｃ
→
＝ａｘ（３ｙ２－２ｘ）＋ａｙｘ
２＋ａｚ２ｚ可以用来表示一个由电流密度为 产生的
场。（每空３分，华中科技大学２００６年）
（５）已知磁感应强度→Ｂ＝→ｅｘ ｍｘ＋ｚ( )２ ＋→ｅｙ ２ｙ＋ｘ( )２ ＋→ｅｚ（２ｚ＋ｙ
２），则 ｍ的值为 。（１分，成
都电子科技大学２００８年）
（６）已知磁感应强度→Ｂ＝→ｅｘｘ
２＋２ｚ＋→ｅｙ ｍｘｙ－( )ｙ＋→ｅｚ ｚ－( )ｘＴ，则 ｍ的值为 。（２分，成都
电子科技大学２０１０年）
２．选择题
（１）在自由空间中，一个孤立的点电荷，其产生的等电位面是 。（２分，南京理工大学
２００８年）
Ａ．平面　　　　　　　　　　　Ｂ．球面　　　　　　　　　　　Ｃ．柱面
（２）若一个矢量函数的旋度恒为零，则此矢量可以表示为某一个（　　）函数。（２分，华南理工大
学２００５年）
Ａ．矢量的散度 Ｂ．矢量的旋度 Ｃ．标量的梯度
—１—
谢处方、饶克谨《电磁场与电磁波》名校真题解析及典型题精讲精练
（３）静电场是（　　）。（２分，华南理工大学２００５年）
Ａ．有散有旋 Ｂ．有旋无散 Ｃ．有散无旋
（３）以下三个矢量函数中，能表示磁感应强度的矢量函数是（　　）。（２分，成都电子科技大学
２０１１年）
Ａ．Ｂ＝ｅｘｙ＋ｅｙｘ Ｂ．Ｂ＝ｅｘｘ＋ｅｙｙ Ｃ．Ｂ＝ｅｘｘ
２－ｅｙｙ
２
（４）己知磁感应强度→ →Ｂ＝ｅｘ ｍｘ＋Ｚ( )２ →＋ｅｙ ２ｙ＋ｘ( )２ →＋ｅｚ（２Ｚ＋ｙ
２），则ｍ的值为（　　）。（２分，成
都电子科技大学２００６年）
Ａ．ｍ＝２ Ｂ．ｍ＝－２ Ｃ．ｍ＝－４
（５）以下矢量函数中，能表示磁感应强度的矢量函数是（　　）。（２分，成都电子科技大学２０１１
年）
Ａ→．Ｂ＝→ｅｘｘ－
→ｅｙ２ｙ＋
→ｅｚ Ｂ→．Ｂ＝→ｅｘｘ＋
→ｅｙ２ｙ＋
→ｅｚ Ｃ→．Ｂ＝→ｅｘｘ－
→ｅｙｙ＋
→ｅｚ
３．判断题
（１）根据Ｅ＝－
!φ，Φ＞０处，Ｅ＜０；Φ＜０处，Ｅ＞０；Φ＝０处，Ｅ＝０。（　　）
（２）法拉第电磁感应定律
!
×Ｅ

＝－Ｂ

ｔ
反映了变化的磁场可以产生变化的电场。（　　）
４．简答题
（１）简述亥姆霍兹定理。（５分，南京理工大学２００８年）
（２）简述电场强度Ｅ
→
、磁场强度Ｈ
→
分别在什么情况下是有散无旋、有旋无散、有散有旋。（６分，华
中科技大学２００６年）
—２—
第二章　静　电　场
静止电荷产生的场分布，只有电场，没有磁场。
· →已知电荷分布 电场；
· →已知电场 电位分布
·电偶极子与极化
·静电场场方程与边界条件
·电容、能量以及电场力。
·已知电荷分布，求场分布
·电荷非对称分布———定义＋叠加原理
·电荷对称分布———高斯定理
一、如图所示，长度为２ａ的线电荷沿ｚ轴放置，其电荷密度为
ρ１＝
ρ０ｚ
２
ａ２
　　－ａ＜ｚ＜ａ
０　　
{
其他
　　
求：
（１）电荷总量Ｑ；
（２）沿ｚ轴上方（ｚ＞ａ）任意一点ｐ的电位和电场；
（３）当Ｐ点位置位于无穷远时（ｚ→"
），计算Ｐ点的电位和电场。
（２０分，北京交通大学２００７年）
二、有半径为ａ的圆形线电荷，其密度为ρ，如图所示，先求中心轴ｄ处的电场强度Ｅ
＾
，并讨论当 ｄ
＝０处的Ｅ
＾
。（１５分，西安电子科技大学２００４年）
三、位于ＸＯＹ平面内的半径为 ａ、圆心在坐标原点的均匀带电圆盘，其面电荷密度为 ρｓ，如图所
—３—
谢处方、饶克谨《电磁场与电磁波》名校真题解析及典型题精讲精练
示，试求圆盘的电位。（１５分，西安电子科技大学２０１２年）
四、放于空气中的无穷大理想导体平面表面上分布有均匀电荷，其面密度为 ρｓ，则其表面处空气
一侧的电场强度的大小为 。（每空３分，华中科技大学２００６年）
五、设相互平行的两无限大带电平面间距为 ｄ，其面电荷密度分别为ρｓｏ和 －ρｓｏ，求空间三个区域
中的电场强度。（５分，成都电子科技大学２００５年）
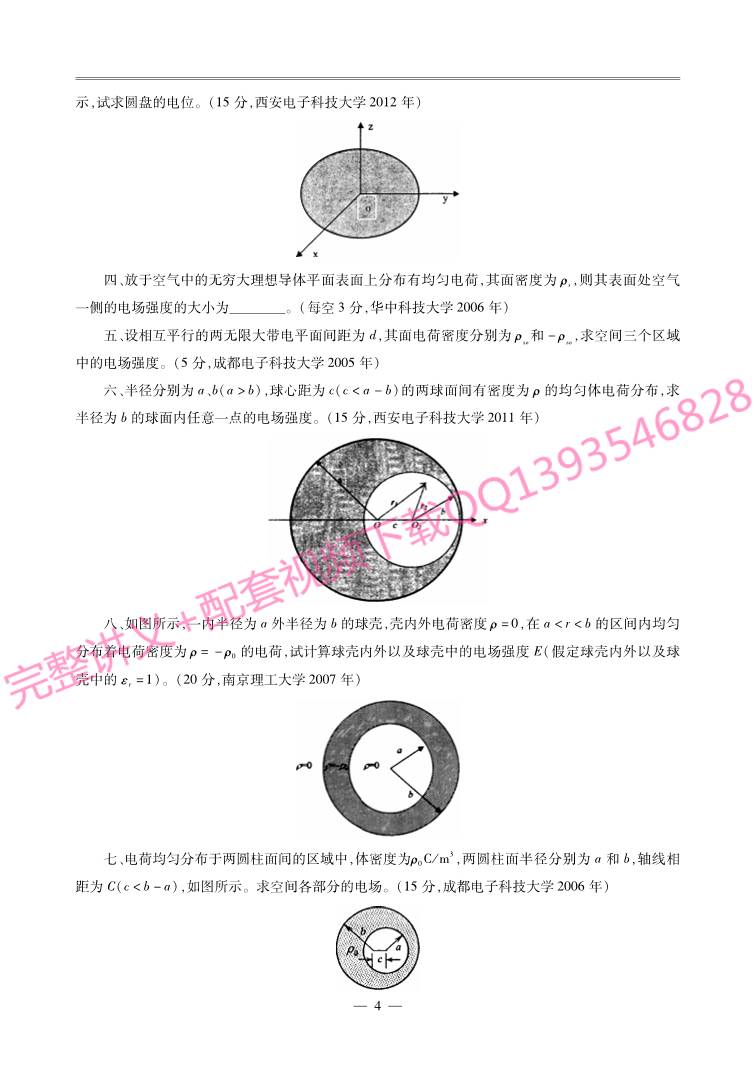
六、半径分别为ａ、ｂ（ａ＞ｂ），球心距为ｃ（ｃ＜ａ－ｂ）的两球面间有密度为 ρ的均匀体电荷分布，求
半径为ｂ的球面内任意一点的电场强度。（１５分，西安电子科技大学２０１１年）
八、如图所示，一内半径为ａ外半径为ｂ的球壳，壳内外电荷密度ρ＝０，在ａ＜ｒ＜ｂ的区间内均匀
分布着电荷密度为ρ＝－ρ０的电荷，试计算球壳内外以及球壳中的电场强度 Ｅ（假定球壳内外以及球
壳中的εｒ＝１）。（２０分，南京理工大学２００７年）
七、电荷均匀分布于两圆柱面间的区域中，体密度为ρ０Ｃ／ｍ
３，两圆柱面半径分别为 ａ和 ｂ，轴线相
距为Ｃ（ｃ＜ｂ－ａ），如图所示。求空间各部分的电场。（１５分，成都电子科技大学２００６年）
—４—
一、已知场分布，求电荷分布
一、半径为ａ的带电球，电场强度为 Ｅｒ＝
ρ０
０
（
ｒ
６－
ｒ３
５ａ２
）Ｖ／ｍ，球内外介电常数均为０，求球内任意
点的电荷密度。（９分，北京交通大学２００４年）
二、两个无限大平行板电极，相距ｄ，已知板间电位为φ＝－
ρ０ｘ
３
６ε０ｄ
＋ Ｖ
ｄ＋
ρ０ｄ
６ε( )
０
ｘ，求极板间体电荷
密度ρ和两极板上面电荷密度ρｓ。（９分，北京交通大学２００４年）
三、一半径３ｍｍ的导体球，处于εｒ＝２．５的媒质中，己知距离球心２ｍ处的电场强度为１ｍＶ／ｍ，求
导体球上的电荷。（１０分，南京理工大学２０１０年）
四、有两个导体球，导体球１的半径为ａ、带电量为２ｑ。导体球２的半径为２ａ、带电量为 －ｑ。设
两球间距离Ｄａ，若用细导线将两球连接起来，则导体球１的带电量为（　　），导体球２的带电量为
（　　）。（每空１分，成都电子科技大学２００９年）
五、只有将电位参考点选择在无穷远处才能是求解电位分布的问题最简单（　　）
六、将电位参考点选择在无穷远处，有可能使求解电位分布的问题最简单（　　）。（１分，成都电
子科技大学２００７年）
七、电位高的地方，电场强度一定大。（　　）（１分，成都电子科技大学２００９年）
八、将一带正电的点电荷ｑ移近一个不接地的导体球时，若以无穷远处为电位参考点，则导体球
的电位将降低。（　　）（１分，成都电子科技大学２００９年）
九、在静电场中，Ａ、Ｂ两点的电位为φＡ＞φＢ，正电荷由 Ａ移动到 Ｂ的过程中，电场力作正功。
（　　）（１分，成都电子科技大学２００９年）
二、介质极化
一、极化强度为Ｐ的介质中，极化（束缚）电荷密度 ρｐ＝ ，极化（束缚）电荷面密度 ρｓｐ＝
。（每空１分，成都电子科技大学２００２年、２００５年）
三、已知介电常数为ε＝２ε０的均匀介质中存在电场强度分布
→Ｅ＝→ｅｘｘ＋
→ｅｙ（２ｙ＋ｘ
２），则介质中的自
由电荷体密度为（　　）、极化（束缚）电荷体密度为（　　）。（每空１分，成都电子科技大学２００８年）
五、在电介质中，电场强度
→Ｅ的散度为零处，也可能存在自由电荷。（　　）（１分，成都电子科技大
学２００９年）
六、根据高斯定理，若闭合曲面Ｓ内没有电荷，则闭合曲面 Ｓ上任一点的场强一定为零。（　　）
（１分，成都电子科技大学２００９年）
七、对于极化强度为Ｐ，体积为 Ｖ及 Ｖ的外表面面积为 Ｓ的介质块，有（　　）。（２分，华南理工
—５—
谢处方、饶克谨《电磁场与电磁波》名校真题解析及典型题精讲精练
大学２００５年）
Ａ．∮Ｓρｓｐ·ｄＳ＋∫ＶρＰ·ｄＶ＝０ Ｂ．∮ＳＰ·ｄＳ＝０ Ｃ．∫ＶρＰ·ｄＶ＝０
八、介质被极化时其表面上不一定处处都出现极化（束缚）电荷（　　）。（１分，成都电子科技大
学２００３年）
九、介质被极化时其表面上有可能出现极化（束缚）电荷（　　）。（１分，成都电子科技大学２００７
年）
十、在均匀极化的电介质中，极化电荷只能分布在电介质表面。（　　）（１分，成都电子科技大学
２００９年）
十一、介质球被均匀极化，已知极化强度为Ｐ＝ａｚＰ０，求束缚电荷的体密度和面密度。（９分，北京
交通大学２００４年）
十二、己知半径为ａ，长度为ｌ的均匀极化介质圆柱内的极化强度Ｐ＝Ｐ０ａｚ，圆柱轴线与坐标 Ｚ轴
重合，试求：
（１）圆柱上的极化电荷面密度ρｓｐ；
（２）在远离圆柱中心的任意一点ｒ处（ｒ＞＞ａ，ｒ＞＞ｌ）的电位ψ；
（３）在远离圆柱的任意一点ｒ处的电场强度Ｅ。（１５分，西安电子科技大学２００７年）
三、方程与边界条件
一、介电常数为ε（ｘ，ｙ，ｚ）的介质区域Ｖ中，静电荷的体密度为ρ（ｘ，ｙ，ｚ），己知这些电荷产生的电
场
→Ｅ＝→Ｅ（ｘ，ｙ，ｚ），下面表达中不成立的是（　　）。（２分，成都电子科技大学２００６年）
Ａ．
!
·
→Ｅ＝ρ／ε Ｂ．
!
·
→Ｅ＝ρ Ｃ．
!
×→Ｅ＝０
二、静电场中引入标量位的条件是（　　）；时变场中引用矢量位的条件是（　　）。（每空１分，
成都电子科技大学２０１１年）
三、空气（介电常数ε１＝ε０）与电介质（介电常数ε２＝４ε０）的分界面试ｚ＝０的平面。若已知空气
中的电磁强度Ｅ１＝ｅｘ２＋ｅｚ４，则电介质中的电场强度应为（　　）。（２分，成都电子科技大学２００７年、
２０１１年）
Ａ．Ｅ１＝ｅｘ２＋ｅｚ１６ Ｂ．Ｅ１＝ｅｘ８＋ｅｚ４ Ｃ．Ｅ１＝ｅｘ２＋ｅｚ
五、理想介质分界面上没有自由电荷，分界面两侧的电场与法线的夹角为 θ１，θ２，介电常数为 ε１，
ε２，此时折射角之间应满足： 。（４分，南京理工大学２００５年）
六、在理想导体表面上，（　　）矢量总是平行于导体表面，（　　）矢量总是垂直于导体表面。
（每空１分，成都电子科技大学２００９年）
四、电容、电场能量
一、任意两个带电导体间都存在电容，对电容有影响的因素是 ，对电容没有影响的因素
是 。（每空１分，成都电子科技大学２００２年）
（可考虑的因素有：①导体的几何性质、②导体上的电荷、③两个导体的相对位置、④空间介质）
—６—
二、在真空中，有一半径为ａ的导体球，带电荷为Ｑ，求这一孤立导体的电容Ｃ。（２０分，西安电子
科技大学２００４年）
三、图为球心在两种介质的界面上、半径为ａ的导体球，若导体球的带电量为 Ｑ，两种介质的介电
常数分别为ε１和ε２，试求：
１．导体球外的电场强度Ｅ；
２．球面上的自由面电荷密度ρｓ；
３．导体球的孤立电容Ｃ０。（１５分，西安电子科技大学２００８年）
四、球形电容器内外导体半径分别为 ａ、ｂ，其间填充介电常数为ε１和ε２的两种均匀介质，如图所
示。设内球带电荷为ｑ，外球接地。求：
（１）介质中的电场和电位分布；
（２）电容器的电容和电场能量。（１５分，成都电子科技大学２０１０年）
十一、体积为Ｖ、介电常数为ε的介质中的电荷分布ρ（ｒ），在空间形成标量位 φ和电场分布 Ｅ和
Ｄ，则空间的静电能量密度为 ，空间的静电能量为 。（每空１分，成都电子科技大学
２００２年、２００５年）
十二、静电场能量可以表示成Ｗ＝１２∫ｖρｄＶ，所以在电荷密度ρ＝０的地方，静电场能量密度也一
定为零（　　）。（１分，成都电子科技大学２００３年，２００７年）
五、理想导体构成的电容器，内外半径分别为ａ，ｂ，长度为ｄ，同轴内填充介质（ε＝９ε０，σ），已知内
外半径间的电压为Ｕ，忽略边际效应。求：
１）内外导体间的电场强度Ｅ；
２）内导体的表面电荷密度ρｓ；
３）电容器的电容Ｃ，用ａ，ｂ，ｄ，ε０表示答案；
４）根据（１）计算电场强度，计算电容器存储的静电能Ｗｅ，并证明Ｗｅ＝
ＣＵ２
２；
５）计算电容器的电阻Ｒ。（２０分，北京交通大学２００７年）
—７—
谢处方、饶克谨《电磁场与电磁波》名校真题解析及典型题精讲精练
六、圆柱体电容器内导体半径为ａ，外导体内半径为 ｂ，两导体间为空气，内外导体间加低频电压
Ｕ０ｓｉｎωｔ，试计算单位长度的该电容器任意时刻存储的电场能量。（９分，北京交通大学２００４年）
七、两个同轴导体圆柱面半径分别为ａ和ｂ，在０＜θ＜θ０部分填充介电常数为ε的电介质，两柱面
间加电压Ｕ０，如图所示。试求：
（１）两柱面间的电场和电位分布；
（２）极化电荷（束缚电荷）分布；
（３）单位长度的电容和电场能量。（１５分，成都电子科技２００２年、２００７年、２０１１年）
—８—
第三章　恒定电流的电场
１．简要分析恒定电场与静电场之间的相同之处和不同之处。（１０分，电子科技大学２０１０年）
２．电导率为σ的导电介质中流有电流 Ｊ，则介质中存在的电场 Ｅ为 。（每空１分，电子
科技大学２００２年）
３．两载面积大小完全相同的一段直铁丝和直铜丝串联后接入一直流电路，假设铁丝和铜丝中的
电流密度和电场强度分别为 Ｊ

１，Ｅ

１和 Ｊ

２，Ｅ

２，则（　　）。（２分，华南理工大学２００５年）
Ａ．Ｊ１＝Ｊ２，Ｅ１＞Ｅ２ Ｂ．Ｊ１＝Ｊ２，Ｅ１＜Ｅ２ Ｃ．Ｊ１＞Ｊ２，Ｅ１＝Ｅ２
４．在恒定电场中，→Ｊ和→Ｅ满足的边界条件分别为 和 。（每空１分，电子科技大学
２００６年）
５．恒定电场中，当（　　）时两种媒质的分界面上的自由面电荷为零。（２分，华南理工大学２００５
年）
Ａ．ε１σ１＝ε２σ２ Ｂ．ε１σ２＝ε２σ１ Ｃ．ε１ε２＝σ１σ２
６．恒定电场中，电源内部存在库仑场Ｅ和非库仑场Ｅ′，两者的作用方向总是相反。（　　）（２分，
华南理工大学２００５年）
７．平板电容器极板面积为 Ｓ，板间距离为 ｂ，极间填充不良导体σ１和σ２，各占一半，如图所示。求
该电容器的漏电导Ｇ。（９分，北京交通大学２００４年）
８．在一块厚度ｄ的导电板上，由两个半径为ｒ１和ｒ２的圆弧和夹角为 α的两半径割出的一块扇形
体，如图所示。求：
（１）沿厚度方向的电阻；
（２）两圆弧面之间的电阻。设导电板的电导率为σ。（１０分，电子科技大学２００８年）
—９—
谢处方、饶克谨《电磁场与电磁波》名校真题解析及典型题精讲精练
第四章　恒定磁场
一、已知电流分布，求磁场
１．电荷的定向运动形成电流，当电荷密度ρ满足ρｔ
＝０时，电流密度Ｊ应满足 ，此时电流
线的形状应为 。（每空１分，电子科大２００３、２００５、２００８）
２．有半径为ａ的圆形线电流，电流为Ｉ，如图所示，现求中心轴 ｄ处的磁感应强度 Ｂ
→
，并讨论 ｄ＝０
处的Ｂ
→
。（提示：利用毕奥－沙伐定律Ｂ
→
＝∫
μ０Ｉｄｌ
→
×ｒ
→
４πｒ３
）（２０分，西电２００４）
４．已知一个半径为ａ的圆柱导体中通有电流 Ｉ，导体的电导率为 σ，请问该导体中存在哪些场？
场强大小为多少？写出导体与自由空间分界面上的边界条件。（５分，电子科大２００５）
７．如图所示，两无限长细直导线相距为 ａ，通以大小相等方向相反的电流，求 ｘ轴线上的磁场强
度。（２０分，南理工２００７）
二、磁介质的磁化
１．磁介质在外磁场的作用下产生磁化的物理机制是什么？磁化介质一般具有什么样的宏观特
征？（１０分，电子科大２００６）
２．磁化强度为Ｍ的磁化体中，磁化（束缚）电流密度体密度ＪＭ＝ ，磁化（束缚）电流面密
度ＪＳＭ＝ 。（每空１分，电子科大２００３）（每空１分，电子科大２００５）
３．已知磁导率为μ的均匀介质中存在恒定（稳恒）磁场分布→Ｂ，则介质中的电流体密度→Ｊ可以表示
成 ，磁化电流体密度Ｊ→ Ｍ可以表示成 。（每空１分，电子科大２００９）（每空２分，电子
—０１—
科大２０１０）
４．半径为ａ的无限长直导体圆柱均匀通过电流Ｉ，外包厚度为 ａ磁导率为 μ的磁介质，求介质包
层外表面的磁化电流。（９分，北交大２００４）
５．如图所示，无限长直导体圆柱由电导率不相同的两层导体构成，内层导体的半径ａ１＝２０ｍｍ，电
导率σ＝２ｘｌ０７Ｓ／ｍ；外层导体的外半径ａ２＝４０ｍｍ，电导率 σ＝ｌ０
７Ｓ／ｍ。导体圆柱中流过的电流为 Ｉ＝
１００Ａ，试求ρ（ρ为到轴线的距离）分别为１０ｍｍ、３０ｍｍ和５０ｍｍ处的磁感应强度→Ｂ。（１８分，电子科大
２００８）
５．将一个半径为ａ、高度为ｄ的铁质（铁的磁导率为μ）圆柱体放置在磁感应强度为→Ｂ０的磁场中，
并使它的轴线与
→Ｂ０平行。分求出ａｄ和ａｄ时，圆柱体内的
→Ｂ和→Ｈ；若己知Ｂ０＝１Ｔ、μ＝３０００μ０，求磁
化强度Ｍ。（１２分，电子科大２００６）
三、场方程与边界条件
１．如图所示，Ｐ为闭路Ｃ上的一点，当Ｃ以外的电流Ｉ２变大时，Ｐ点的磁场强度也会发生变化，闭
合回路Ｃ上的积分∮ＣＨ·ｄｌ＝（　　）。（２分，华南理工２００５）
Ａ．Ｉ１ Ｂ．Ｉ２ Ｃ．Ｉ１＋Ｉ２
２．在两种不同媒质的分界面上，若不存在面分布电荷，则电位移矢量的（ ）分量是连续
的；若不存在面分布电流，则磁场强度矢量的（ ）分量是连续的。（每空２分，电子科大２０１０）
５．证明在不同介质分界面上，矢量磁位Ａ的切向分量连续。（１５分，南理工２００８）
６．假设同轴线内、外导体半径分别为 ａ和 ｂ，内、外导体问填充 μ１、μ２两种介质并各占一半的空
间，求内、外导体间的磁场强度。（１０分，南理工２０１０）
８．设Ｚ＜Ｏ和Ｚ＞Ｏ的两个半无限大空间分别充满磁导率为μ１和 μ２的均匀磁介质，在界面上有
一线电流Ｉ，试求：
—１１—
谢处方、饶克谨《电磁场与电磁波》名校真题解析及典型题精讲精练
（１）空间的磁场强度Ｈ；
（２）空间的磁场强度Ｂ；
（３）Ｚ＝０平面上的磁化面电流密度Ｊｍｓ。（１５分，西电２００６）
四、电感与磁场能量
１．两个导体回路Ｃ１和Ｃ２构成一个系统，其中Ｃ１的自感与（　　）无关。（２分，电子科大２００６）
Ａ．两个回路的相对位置 Ｂ．空间的介质 Ｃ．回路Ｃ１的几何形状
２．两个载流线圈之间存在互感，对互感没有影响的是（　　）。（２分，电子科大２００７）（２分，电子
科大２０１１）
Ａ．线圈的尺寸 Ｂ．两个线圈的相对位置 Ｃ．线圈上的电流
３．任意两个载流线圈之间都存在互感（互感系数），对互感有影响的因素是（　　），对互感没有
影响的因素是（　　）。
（可考虑的因素有：线圈的几何形状；线圈上的电流；两个线圈的相对位置；空间介质）（每空１分，
电子科大２００３）（每空１分，电子科大２００５）
４．根据恒定磁场能量计算公式：Ｗｍ＝
１
２∑
ｎ
ｋ＝１
φｋＩｋ可知，Ｉ＝０的区域内磁场能量为０。（　　）（２分，
华南理工２００５）
６．如图所示，一无限长载流直导线与一长方形导线框在同一平面上，求直导线与导线框之间的互
感Ｍ。（１５分，华南理工２００５）
７．如题六图所示，ｘ＜０的半空间充满磁导率为 μ的磁介质，ｘ＞０的半空间为空气。有一无限长
直细导线位于ｚ轴上，导线中的电流为Ｉ。在ｘｏｚ平面内有一个与细导线共面的矩形线框。试求：
（１）电流Ｉ产生的磁感应强度；
（２）细导线与矩形线框间的互感。（１５分，电子科大２００９）
８．无限长直导线附近有一共面的矩形线框，尺寸为ａｂ，与直导线相距ｃ，如图１所示。
（１）求直导线与线框之间的互感；
—２１—
（２）若线框绕直导线旋转θ角，试说明直导线与线框之间的互感有无变化？
（３）若线框绕自身的中心轴线旋转θ角，试说明直导线与线框之间的互感有无变化？（１２分，电
子科大２００５）
１４．有一内导体半径为ａ，外导体的内半径为ｂ的无限长同轴线，其内由磁导率分别为μ１和μ２两
种磁介质以图１所示的方式填充。如若给该同轴线通恒定电流Ｉ，试求：
（１）内外导体间的磁场强度Ｈ；
（２）两种磁介质界面上的磁化面电流密度Ｊｍｓ；
（３）内外导体间的磁能密度ｗｍ。（１５分，西电２００５）
１３．同轴线的内导体是半径为ａ的圆柱，外导体是半径为 ｂ的薄圆柱面，其厚度可忽略不计。内
外导体间填充有磁导率分别为μ１和μ２两种不同的磁介质，如图４所示。设同轴线中通过的电流为
Ｉ，试求：
（１）同轴线中单位长度所储存的磁场能量；
（２）单位长度的自感。（１５分）
１６．半径为ａ的两对无限长的平行双线传输线上下水平放置，截面如图所示，图中 ｂ为每对双线
两轴线间的距离，ｄ为两对双线上下放置时轴线间的距离，且ｂ＞＞ａ，ｄ＞＞ａ．求两对传输线之间的单
位单位长度的互感。（２０分，北交大２００７）
—３１—
谢处方、饶克谨《电磁场与电磁波》名校真题解析及典型题精讲精练
１０．如图２所示，无限长直导线中的电流为Ｉ１，附近有一个载有电流Ｉ２的正方形回路，此回路与直
导线不共面。试求：
（１）直导线与矩形回路间的互感Ｍ；
（２）矩形回路受到磁场力→Ｆｍ，并证明
→Ｆｍ＝－
→ｅｙ
μ０Ｉ１Ｉ２
槡２３π
。（１６分，电子科大２０１１）
９．无限长细导线中载有电流Ｉ１，附近有一共面的矩形线框，载有电流Ｉ２。求：
（１）系统的互感；
（２）当矩形线框绕其对称轴转动到图４－ｂ所示位置时，系统能量的改变量为多少？
（３）定性分析在图４－ｂ所示位置时，矩形线框的各边的受力情况，由此说明矩形线框的运动趋
势。（共１５分，电子科大２００２）
１５．如图所示的矩形截面磁环上均匀密绕Ｎ匝线圈，磁环的相对磁导率为μｒ。计算该磁环的外自
感。（２０分，华中科技２００６）
—４１—
第五章　静态场的解
一、静态场的边值问题及解的唯一性定理
二、镜像法
三、分离变量法
一、唯一性定理
１．简述静电场边值问题的唯一性定理？它的意义何在？（１０分，成都电子科大２００５）
２．简述唯一性定理。（１０分，南理工２００７）
３．静电场边值问题的唯一性定理说明了什么？它的意义何在？（１０分，成都电子科大２００７）
４．简述静电场边值问题的唯一性定理，并举例说明唯一性定理在求解静场边值问题中的重要作
用。（１０分，成都电子科大２００９）
５．对于一个已知的边值问题，有多种不同的方法可以用来求解。要使所得的结果都是正确的，求
解时应该保（　　）和（　　）不变。（每空１分，成都电子科大２０１１）
８．对于一个已知的边值问题，有多种不同方法可以用来求解，而所得的结果都是一样的。写出任
意三种求解静电场边值题的方法： 、 、 。（每空１分，电子科大２００３）（每空
１分，电子科大２００５）
二、镜像法
１．镜像法（电像法）是一种简单而有效的边值问题求解方法，说明其基本思想以及像电荷选择的
原则。（１０分，成都电子科大２００３）
２．简要说明镜像法的基本思想及镜像电荷选择的原则。（１０分，华南理工２００５）（１０分，成都电
子科大２００６）
３．描述镜像法的基本思想；写出应用镜像法求解静态场问题时确定镜像电荷需要遵循的原则。
（６分，南理工２０１１）
４．镜像法是在所求场的区域 （Ａ．之内；Ｂ．之外），用一些 （Ａ．假想电荷；Ｂ．真实
电荷）来代替场问题的边界。这些电荷和场区域原有的电荷一起产生的电场必须要满足原问题的边
界条件。镜像法属于 （Ａ．解析法；Ｂ．数值方法）。（每空２分，南理工２００８）
５．用镜像法求解静电场边值问题时，判断镜像电荷设置是否正确的依据是（　　）。（２分，电子
科大２００７）
Ａ．镜像电荷的位置是否与原电荷对称
—５１—
谢处方、饶克谨《电磁场与电磁波》名校真题解析及典型题精讲精练
Ｂ．镜像电荷是否与原电荷等值异号
Ｃ．待求区域内的电位函数所满足的方程与边界条件是否保持不变
７．任意电荷的像电荷总是与其等量异号（　　）。（１分，电子科大２００３）
７．写出至少三种求解静电场边值问题的方法名称，分别对这些方法的基本思想和优缺点做出简
要说明。（６分，电子科大２００２）
１１．折成直角的接地导体角域内（１，１）点有一带电量为 ｑ点电荷，求该点电荷所受的静电力。（９
分，北交大２００４）
６．两块成６０°的接地导电板，角形区域内有点电荷 ＋ｑ，若用镜像法求解区域的电位分布，共有
个像电荷，其中电荷量为＋ｑ的像电荷有 个。（每空１分，电子科大２０１１）
９．一半径为ａ的接地薄导体球壳内，距球心为ｄ（ｄ＜ａ）处有一点电荷 ＋Ｑ，导体球壳内表面上感
应的电荷总量是（　　）。（每题２分，电子科大２００６）
Ａ．－Ｑ Ｂ．－ｄＱ／ａ Ｃ．－ａＱ／ｄ
１０．在点电荷＋ｑ产生的静电场中，在距离该点电荷ｄ处放入一个半径为Ｒ的导体球，且导体球不
接地。则在球面上靠近点电荷一侧将布有 电荷，该电荷的总量为 ，导体球的电位为
。（每空３分，华中科技２００６）
１２．如图所示，在均匀外电场Ｅ０中，放置一个电荷，带电量为 ｑ，与接地导体平面相距为 ｄ，当电荷
ｑ所受的电场力为０时，ｄ的值为多大？（１０分，北交大２００７）
１５．半径为ａ导体球外距球心ｄ处放置一点电荷ｑ，如图２所示。（１５分，电子科大２００５）
（１）若导体球接地，求点电荷ｑ受到的静电力；
（２）若导体球未接地且带有电荷Ｑ，求点电荷ｑ受到的静电力。并证明：当Ｑｑ＝
ａ３（２ｄ２－ａ２）
ｄ（ｄ２－ａ２）２
时，点
电荷ｑ受到的静电力为零。
—６１—
１７．点电荷ｑ位于半径为ａ的导体球直径延长线上，距球心ｄ（ｄ＞ａ），如图所示。求：
（１）空间的电位分布；
（２）点电荷所受到的静电力；
（３）如果导体球接地，重新解答上面２个问题。（１５分，电子科大２００７）
１９．点电荷ｑ位于一个半径为ａ的不接地导体球外，距球心为２ａ。试求：
（１）导体球面上Ａ、Ｂ两点的感应电荷密度；
（２）点电荷ｑ受到的静电力。（１８分，电子科大２００９）
１４．两个点电荷 ±ｑ位于半径为 α的导体球直径延长线上，分别距球心 ±ｄ（ｄ＞ａ），如图所
示。求：
（１）空间的电位分布；
（２）两个点电荷分别所受到的静电力；
（３）两个点电荷的镜像电荷所构成的中心位于球心的电偶极子的电偶极矩；
（４）如果导体球接地，上面３个问题的结果如何改变，为什么？（１８分，电子科大２００３）
１３．接地空心导体球的内外半径分别为ａ和ｂ，如图３所示。
（１）如果在空腔中距球心ｄ处放置一个点电荷ｑ，求导体球内外的电位分布和点电荷ｑ受到的静
电力；
（２）如果在导体球外距球心Ｄ处放置一个点电荷 Ｑ，求导体球内外的电位分布和点电荷 Ｑ受到
的静电力；
（３）如果两个点电荷同时存在，导体球内外的电位分布和两个点电荷受到的静电力有何变化？
（共１５分，电子科大２００２）
—７１—
谢处方、饶克谨《电磁场与电磁波》名校真题解析及典型题精讲精练
１６．不接地空心导体球的内、外半径分别为ａ和ｂ，在空腔内距球心为ｄ１（ｄ１＜ａ）处放置点电荷ｑ１，
在球外距球心为ｄ１（ｄ１＞ｂ）处放置点电荷ｑ２，且ｑ１、ｑ２与球心共线，如图题五所示。求点电荷ｑ１和ｑ２分别
受到的电场力。（１８分，电子科大２００６）
２３．如图１所示，导体球壳与无限大接地导体平面镶嵌，球壳内外半径分别为 ａ和 ｂ，在球壳内外
分别有点电荷ｑ１和ｑ２，，距球心的距离分别为ｄ１和ｄ２，求：球壳内外空间区域中的电位函数。（２０分，
西工大２００７）
三、分离变量法
１．直角坐标系下的分离变量法中，分离常数Ｋ２ｘ＜０，ｆ（ｘ）的通解形式为： 。（４分，华南理
工２００５）
３．图示为一长方形截面的导电槽，槽可以视为无限长，其上有一块与槽绝缘的盖板，已知槽电位
为零，盖板的电位为Ｕ０ｓｉｎ
２πｘ
ａ，求槽内的电位函数。（１２分，北交大２００４）
４．一个Ｚ方向无限长、横截面为ａｘｂ的矩形金属管，其三个边的电位为零，第四边与其它边绝缘，
电位是１０ｓｉｎ（πｘａ），如图所示，试求管内的电位分布。（１５分，西电２０１２）
５．有一如图所示之０≤ｘ≤ａ，０≤ｙ≤ａ的矩形区域，其边界上的电位分布为：φ（０，ｙ）＝０，φ（ａ，ｙ）
—８１—
＝０，φ（ｘ，０）＝０，φ（ｘ，ｂ）＝Ｕ０ｓｉｎ
３πｘ
ａ（式中Ｕ０为实常数），试求矩形区域内的 φ（ｘ，ｙ）。（１５分，西电
２００５）
２．沿ｘ方向无限长的槽形电极如图所示，域内无空间电荷分布，试求场域内电位分布。已知边界
条件如下：
１）在ｘ＝０处，电位Φ ＝Ｕ０；
２）在ｙ＝０处，电位Φ＝０；
３）在ｙ＝ｂ处，电位Φ ＝Ｕ０。（２０分，北交大２００７）
６．在一矩形接地金属管中，ｘ＝０处，电位 Φ＝１００ｓｉｎ２πｂｙ的中心板，该板与上下壁绝缘，求：金属
管中的电位函数？（１５分，西工大２００７）
—９１—
谢处方、饶克谨《电磁场与电磁波》名校真题解析及典型题精讲精练
第六章　时变电磁场
一、场方程与边界
二、电磁场的位函数
三、电磁能量守恒定律
四、时谐电磁场
一、场方程与边界条件
１．写出麦克斯韦方程组，并说明其意义所在。（１０分，华南理工２００５）
２．写出麦克斯韦方程组的微分形式，并讨论时变电磁场的特点。（１０分，电子科大２００６）
３．写出麦克斯韦方程组的微分形式以及积分形式。（１０分，南理工２００７）
４．写出微分形式麦克斯韦方程组。（５分，南理工２０１１）
５．写出介质中的麦克斯韦方程组微分形式，并说明时变电磁场的特点。（１０分，电子科大２００９）
６．写出介质中的麦克斯韦方程组，讨论时变电磁场的特点，并且说明麦克斯韦方程组的意义所
在。（１５分，电子科大２００３）
７．写出时变电磁场的积分形式麦克斯韦方程并推导出其微分形式。（５分，南理工２００８）
１５．写出麦克斯韦方程组的微分形式，由麦克斯韦方程组的两个旋度方程和电荷守恒定律导出两
个散度方程。（２０分，南理工２０１０）
９．电流连续性方程能由麦克斯韦方程组导出吗？如果能，试推导之；若不能，说明原因。（１０分，
电子科大２００８）
１０．试由麦克斯韦方程组推导出电流连续性方程
!
·Ｊ＝－ρ
ｔ
。（１２分，北交大２００４）
１６．利用矢量恒等式
!
×
!
×Ａ＝
! !
·( )Ａ －
!
２Ａ，推导存在电荷密度 ρ和电流密度 Ｊ的均匀、线
性、各向同性、无耗媒质中的Ｅ和Ｈ的波动方程。（２０分，南理工２００７）
１７．什么是位移电流？它是如何引入的？位移电流与传导电流有何本质上的区别？（１０分，电子
科大２００５）
１９．已知自由空间中Ｅ
→
＝１００ｃｏｓ（３×１０９ｔ－１０ｚ）ａｙ，求空间位移Ｊｄ。（５分）
２０．球形电容器内、外导体半径分别为ａ和 ｂ，外加一正弦电压 Ｕ０ｓｉｎωｔ，且 ω不大，电场分布和静
电场情形相同，内、外导体间的介质的相对介电常数为εｒ，求：
（１）介质中的位移电流密度；
—０２—
（２）穿过半径为ｒ（ａ＜ｒ＜ｂ）的球面的总位移电流ｉＤ。（１５分，华南理工２００５）
２１．证明通过任意闭合曲面的传导电流和位移电流的总量为０。（１０分，南理工２０１１）
２２．导电媒质中存在时谐电磁场时，其传导电流和位移电流的相位差为（　　）。（每空１分，电子
科大２０１１）
２３．导电媒质中的传导电流Ｊｃ与位移电流Ｊｄ的相位（　　）。（２分，电子科大２００７）
Ａ．相同 Ｂ．相反 Ｃ．相差９０°
８．当一个闭合线圈在某外加磁场中运动时，什么情况下线圈内会产生感生电流？什么情况下不
会产生感生电流？为什么？（６分，电子科大２００２）
１１．磁导率为μ的介质（物质）中有传导电流分布 Ｊ（ｒ），则空间任意点磁场强度 Ｈ的旋度为
，磁感应强度Ｂ为 。（每空１分，电子科大２００２）
１３．只要闭合线圈在磁场中做切割磁力线的运动，线圈中一定会形成感生电流（　　）。（１分，电
子科大２００３）（１分，电子科大２００７）（１分，电子科大２００９）
１４．电场一定是由电荷产生，而磁场一定是由电流产生（　　）。（１分，电子科大２００３）（１分，电
子科大２００７）
２９．在静电场中电力线不是闭合的曲线，所以在交变场中电力线也是非闭合的曲线。（　　）（２
分，华南理工２００５）
３０．以下关于时变电磁场的叙述中，不正确的是（　　）。（２分，电子科大２００７）
Ａ．电场是有旋场 Ｂ．电场和磁场互相激发 Ｃ．磁场是有源场
２５．什么是均匀媒质？什么是各项同性媒质？什么是线性媒质？（６分，华中科技２００６）
２８．（２０分，南理工２０１０）由麦克斯韦方程出发导出两不同媒质的边界条件：ｅｎ·（Ｅ１－Ｅ２）＝ρｓｅｎ
×（Ｅ１－Ｅ２）＝０
３２．时变电磁场中，在理想导体表面，（２分，华南理工２００５）
Ａ．电场与磁场的方向都垂直于表面
Ｂ．电场的方向垂直于表面，磁场的方向都平行于表面
Ｃ．电场的方向平行于表面，磁场的方向垂直于表面
３３．在两种不同媒质的分界面上， 矢量的切向分总是连续的； 矢量的法向分量
总是连续的。（每空１分，电子科大２００５）
２７．在真空中，已知电场Ｅ
→
＝ｙ
＾
Ｅ０ｓｉｎ
πｘ( )ａ ｅ－ｊβｚ，其中 ｙ＾表示 ｙ方向的单位矢量，求磁场 Ｈ
→
。（２０分，
西电２００４）
７．在由理想导电壁限定的区域（０≤ｘ≤ａ）
内存在一个如下的电磁场：
Ｅｙ＝Ｈ０μω
ａ( )π ｓｉｎｋｚ－ω( )ｔ
—１２—
谢处方、饶克谨《电磁场与电磁波》名校真题解析及典型题精讲精练
Ｈｘ＝－Ｈ０ｋ
ａ( )π ｓｉｎπｘ( )ａ ｓｉｎｋｚ－ω( )ｔ
Ｈｚ＝Ｈ０ｃｏｓ
πｘ( )ａ ｃｏｓｋｚ－ω( )ｔ
求：（１）坡印廷矢量的平均值；
（２）导电壁上的电荷密度。（１２分，北交大２００４）
２６．同轴电缆内外半径分别为ａ＝１ｍｍ，ｂ＝３ｍｍ，其间填充τ＝６的绝缘材料，内外导体间的电场
强度为：Ｅ＝１００
τ
ｃｏｓ（３×１０８ｔ－２．４５ｚ）ａｔＶ／ｍ。求：
（１）内导体表面的面电荷密度；
（２）其中磁感应强度Ｂ为大？
（３）该同轴电缆单位长度的电容。（２０分，西工大２００７）
１２．磁力线一定是闭合的（　　）。（１分，电子科大２００３）（１分，电子科大２００７）
１８．麦克斯韦通过数学方法引入 ，从而建立了完整的麦克斯韦方程组。（１分，电子科大
２００３）
２４．分别写出时变电磁场在理想介质和理想导体分界面上的边界条件。（６分，南理工２０１１）
３１．已知Ｚ＝０平面上的电位分布为ｆ（ｘ，ｙ）＝Φ０ｓｉｎ３ｘｃｏｓ４ｙ，求上半空间（Ｚ＞０）的电位分布。（５
分）
３４．在理想导体与理想介质的分界面上，电场强度Ｅ

的切向分量是不连续的。（　　）（２分，华南
理工２００５）
３５．导电率不为零的介质一定是导体（　　）。（１分，电子科大２００３）
二、电磁场的位函数
１．在时变电磁场中是如何引入动态位→Ａ和φ的？→Ａ和 φ不惟一的原因何在？怎样才能使得→Ａ和 φ
是惟一的？（１０分，电子科大２００９）
２．用一组矢量位Ａ和标量位φ可以完整的描述电磁场，但是位函数一般是不唯一的，如要得到一
组唯一确定的位函数，可以规定 。（每空１分，电子科大２００３）（每空１分，电子科大２００５）
６．（１）写出洛伦兹条件；
（２）说明为什么引入洛伦兹条件？
（３）利用洛伦兹条件及矢量恒等式（２０分，南理工２０１１）
!
×
!
×Ａ
→
＝
!
（
!
·Ａ
→
）－
!
２Ａ
→
推导达朗贝尔方程
!
２Ａ
→
－εμ
２Ａ
→
ｔ２
＝－μＪ
→
和
!
２φ－εμ
２φ
ｔ２
＝－ρ
ε
３．在应用电磁场的位函数时，如果不采用洛伦兹规范，而采用所谓的库仑规范，即利用条件
!
·Ａ
＝０，导出此时矢量位Ａ和标量位φ所满足的微分方程。（１５分，电子科大２００３）
—２２—
５．在无源自由空间中，如果已知时变电磁场的矢量磁位 Ａ（ｒ），证明其电场强度为： ( )Ｅ ｒ＝
ｋ２Ａ＋
!
（
!
·Ａ）
ｊωμ０ε０
，其中ｋ＝ω μ０ε槡 ０。（１５分，南理工２００８）
４．试通过定义罗仑兹规范条件证明：在无源空间（即ρ＝０，Ｊ＝０），时谐电场与磁场可以同时用一
个满足形如
!
２Ａｍ＋ω
２μεＡｍ＝０的波动方程的矢量函数Ａｍ表示为：Ｅ＝－
１
ε!
×Ａｍ，Ｈ＝－ｊωＡｍ＋
!
（
!
·Ａｍ）
ｊωμε
，并写出你所定义的罗仑兹规范条件。
三、电磁能量守恒定律
１．坡印亭定理的表达式为： 。（每小题４分，华南理工２００５）
５．利用矢量恒等式
!
· Ａ×( )Ｂ ＝Ｂ·（
!
×Ａ）－Ａ·
!
×( )Ｂ，由麦克斯韦方程组推导均匀、线性、
各向同性媒质中坡印廷定理。（２０分，南理工２００７）
３．坡印廷定理是关于电磁能量的守恒定理，其中单位时间内体积Ｖ中减少的电磁能量 ，
单位时间内流出体积Ｖ的电磁能量为 。（每空１分，电子科大２０１１）
４．区域Ｖ全部用无损耗媒质填充，当此区域中的电磁场能量减少时，一定是（　　）。（２分，电子
科大２００７）
Ａ．能量流出了区域 Ｂ．能量在区域中被损耗 Ｃ．电磁场做了功
６．设电场强度和磁场强度的瞬时值分别为Ｅ＝Ｅ０ｃｏｓωｔ＋φ( )ｅ和Ｈ＝Ｈ０ｃｏｓωｔ＋φ( )ｍ 。
试证明其构成的坡印廷矢量的平均值为Ｓａｖ＝
１
２Ｅ０×Ｈ０ｃｏｓφｅ－φ( )ｍ 。（１５分，南理工２００８）
８．如图所示，同轴线的内导体半径为ａ、外导体的内半径为 ｂ，其间填充均匀的理想介质。设内外
导体间外加缓变电压为ｕ＝Ｕｍｃｏｓωｔ，导体中流过缓变电流为ｉ＝Ｉｍｃｏｓωｔ。
（１）在导体为理想导体的情况下，计算同轴线中传输的平均功率；
（２）当导体的电导率σ为有限值时，定性分析对传输功率的影响。（１５分，电子科大２００９）
９．由半径为ａ的两圆形导体平板构成一平行板电容器，间距为ｄ，两板间满足电常数为ε、电导率
为σ的媒质，如图４所示。设两板间外加缓变电压ｕ＝Ｕｍｃｏｓωｔ，略去边缘效应，试求：
（１）电容器内的瞬时坡印廷矢量和平均坡印廷矢量；
（２）证明进入电容器的平均功率等于电容器内损耗的平均功率。（１８分，电子科大２０１０）
—３２—
谢处方、饶克谨《电磁场与电磁波》名校真题解析及典型题精讲精练
第七章　均匀平面电磁波
一、理想介质中的传播
１．什么是均匀平面波？在理想介质中，均匀平面波具有什么传播特性？（１０分，电子科技大学
２００５）
１５．简述均匀平面波的相速、群速和能速分别表示的物理意义。（６分，华中科技大学２００６）
２．若平面电磁波在空气中的波长λ０＝２ｍ，则在理想介质（ε＝４ε０、μ＝μ０、σ＝０）中传播时，其波长
λ＝ 。（每空１分，电子科技大学２００５）
３．频率ｆ＝５０ＭＨｚ的均匀平面波在某理想介质（介电常数ε＝εｒε０、磁导率μ＝μ０、电导率σ＝０）中
传播时，其波长λ＝４ｍ，则εｒ＝ 。（每空２分，电子科技大学２０１０）
４．若均匀平面波在空气中的相位常数β０＝２ｒａｄ／ｍ，则在理想介质（ε＝４ε０、μ＝μ０、σ＝０）中传播
时，其相位常数β＝ ｒａｄ／ｍ。（每空１分，电子科技大学２００８）
５．若平面电磁波在空气中的波长λ０＝２ｍ，则在理想介质（ε＝４０、μ＝μ０、σ＝０）中传播时，其相位
常数β＝ ｒａｄ／ｍ。（每空１分，电子科技大学２０１１）
６．在理想介质中的均匀平面电磁波，其电场方向与磁场方向相互 ，其振幅之比等于
。（４分，华南京理工大学大学２００５）
７．真空中存在一均匀平面波，一个电量为ｑ的点电荷在该平面波场中以速度ｖ运动，则该电荷所
受的电场力与所受的最大磁场力之比为 。（每空３分，华中科技大学２００６）
８．一个均匀平面波的电场强度矢量为Ｅ＝（ａ
→
ｘ＋ａｙｊ槡２－ａｚ）Ｅ０ｅ
－ｊπ（ｘ＋ｚ）（Ｖ／ｍ），则用单位矢量表示
的该平面波的传播方向 。（３分，华中科技大学２００６）
９．已知α，β＞０，以下那些波描述了沿 ＋Ｚ方向传播的均匀平面波。（每空２分，南京理工大学
２０１１）
Ａ．ｅ
→
ｘｅ
（－α－ｊβ）ｚ 　　　　　　Ｂ．（ｅ
→
ｘ－ｊｅ
→
ｙ）ｅ
－ｊβｚ
Ｃ．ｅ
→
ｙ１００ｓｉｎ（
π
２ｘ）ｅ
－ｊβｚ 　　　　　　Ｄ．－ｅ
→
ｘｃｏｓ（－３×１０
８ｔ－βｚ）
１０．均匀平面波的等相位面和等振幅面都是平面且重合（　　）。（１分，电子科技大学 ２００３、
２００５、２００７）
１１．ＴＥＭ波一定是均匀平面波。（　　）（１分，电子科技大学２００９）
１２．频率ｆ＝５０ＭＨｚ的均匀平面波在某理想介质（介电常数 ε＝４ε０，磁导率 μ＝μ０，电导率 σ＝０）
—４２—
中传播时，波速（　　）。（２分，电子科技大学２００７）
Ａ．等于光速ｃ Ｂ．等于ｃ／２ Ｃ．等于ｃ／４
１３．在无源的空气中，已知均匀平面波的电场和磁场为→Ｅ＝→Ｅ０ｅ
－→ｊｋ·→ｒ和→Ｈ＝→Ｈ０ｅ
－→ｊｋ·→ｒ，式中→ｋ，→Ｅ０，
→Ｈ０均
为常矢量，则一定有（　　）。（２分，电子科技大学２００６）
Ａ→．Ｅ０×
→Ｈ０＝０ Ｂ．→．Ｅ０·
→Ｈ０＝０ Ｃ→．ｋ×→Ｅ０＝０和
→ｋ×→Ｈ０＝０
２０．在理想介质中一均匀平面波的电场强度为 ( )Ｅｔ＝ｅｘ５ｃｏｓ２π１０
８ｔ－( )[ ]ｚ ( )Ｖ／ｍ，
（１）求介质中的波长和自由空间波长；
（２）已知介质μ＝μ０，ε＝ε０εｒ，求介质的εｒ；
（３）写出磁场强度的瞬时表达式；
（４）求瞬时坡印亭矢量和平均坡印亭矢量。（２０分，南京理工大学２００８）
２４．均匀平面电磁波在 μｒ＝１的理想介质中传播，其电场强度为 Ｅ（ｒ，ｔ）＝ａｘｃｏｓ［２π（１０
８ｔ－ｚ）＋
π
５］（Ｖ／ｍ），试求：
（１）该理想介质的相对介电常数εｒ；
（２）平面电磁波的相速度Ｖｐ；
（３）平面电磁波坡印廷（Ｐｏｙｎｔｉｎｇ）矢量的平均值Ｓａｖ。（１５分，西安电子科技大学２００５）
２９．均匀平面电磁波在μｒ＝１的理想介质中传播，若电磁波的电场的瞬时值为 Ｅ（ｒ，ｔ）＝ａｘ３０πｃｏｓ
［２π（１０８ｔ－０．５ｚ）＋π３］（Ｖ／ｍ），试求：
（１）该理想介质的波阻抗η；
（２）理想介质中单位体积内电磁能量的平均值Ｗａｖ；
（３）坡印廷矢量的平均值Ｓａｖ（ｒ）。（１５分，西安电子科技大学２００８）
２６．相对磁导率μｒ＝１的理想介质中传播着电场瞬时值为Ｅ（ｒ，ｔ）＝３０π（槡３ａｘ＋ａｚ）ｃｏｓ［３×１０
８ｔ－
π（ｘ 槡－３ｚ）］Ｖ／ｍ的均匀平面电磁波，试求：
（１）该波的波长λ；
（２）理想介质的相对介电常数εｒ；
（３）该波坡印廷矢量的平均值Ｓａｖ。（１５分，西安电子科技大学２００６）
２３真空中传播的均匀平面电磁波的电场复矢量振幅为Ｅ（ｒ）＝３７７（ａｘ＋ｊ０．８ａｙ＋ｊ０．６ａｚ）ｅ
－ｊπ（３ｙ－４ｚ）
（Ｖ／ｍ），试求：
（１）波传播方向的单位矢量ｎ；
（２）波的磁场复振幅矢量Ｈ（ｒ）：
（３）波的角频率ω。（１５分，西安电子科技大学２００５）
２５．真空中传播的均匀平面电磁波的电场复矢量振幅为：Ｅｒ＝４０π（ａｘ＋ｊ４ａｙ＋ｊ３ａｚ）ｅ
－ｊπ（０．６ｙ－０．８ｚ）
ｍＶ／ｍ，试求：
—５２—
谢处方、饶克谨《电磁场与电磁波》名校真题解析及典型题精讲精练
（１）波传播方向的单位矢ｎ；
（２）波的频率ｆ；
（３）波的磁场强度的瞬时值Ｈ（ｒ，ｔ）。（１５分，西安电子科技大学２００６）
１４．自由空间中传播的均匀平面波，已知磁场强度为 Ｈ＝ 槡－３ａｘ＋ａｙ 槡＋２３ａ( )ｚ ｅ
－ｊπ２ ３ｘ 槡－３ｙ＋２( )ｚＡ／
ｍ。求：
（１）电场Ｅ；
（２）相移常数β和波长λ；（１２分，北方交通大学２００４）
１６．已知自由空间中一平面波的磁场为Ｈ＝１０－６ ３２ａｘ＋ａｙ＋ａ( )ｚｃｏｓｗｔ＋π（ｘ－ｙ－ｃｚ[ ]）Ａ／ｍ，Ｃ为
待定系数，求：
（１）波的传播方向；
（２）波长和频率；
（３）平均坡印廷矢量。（２０分，北方交通大学２００７）
１８．在无源的空气中，已知电磁场波的频率 ｆ＝３×１０９Ｈｚ、磁场强度为→Ｈ ｘ，( )ｚ＝→ｅｙ０．１ｓｉｎ
１０π( )ｘｅ－ｊｋｚＡ／ｍ，试求：
（１）常数ｋｚ；
（２）电场强度复矢量→Ｅ（ｘ，ｚ）和瞬时矢量→Ｅ（ｘ，ｚ；ｔ）；
（３）平均坡印廷矢量→Ｓａｖ（ｘ，ｚ）。（１５分，电子科技大学２０１１）
３３．已知在自然空间中有一频率为３ＧＨｚ的时变场，其矢量磁位Ａ＝１０ｓｉｎ（ωｔ－ｋｚ）
)
ａｘ，求：
（１）电场强度和磁场强度；
（２）角频率ω，波长λ，相位常数ｋ，相速ｖｐ，波的传播方向；
（３）波印廷矢量的瞬时值。（２０分，西北工业大学２００７）
一、有耗媒质中的电磁波
１．设电磁波在海水中的穿透深度为 δ，则海水的衰减常数 α为 。（１分，电子科技大学
２００２）
１８．电磁波在无损耗（非导电）和有损耗（导电）的无界空间传播时分别具有什么特点？重点分析
它们的不同之处及其产生原因。（６分，电子科技大学２００２）
８．何为良导体？何为良介质？（６分，华中科技大学２００６）
２．均匀平面波在某媒质（介质）中传播，当电磁波的电场强度 Ｅ与磁场强度 Ｈ不同相时，这种媒
质（介质）一定是（　　）。（每空１分，电子科技大学２００３、２００５、２００９）
３．均匀平面波在导电媒质中传播时，电场和磁场的振幅将随传播距离的增加而按规律衰减，且磁
场强度的相位与电场强度的相位。（１分，电子科技大学２００５）
４．均匀平面波在导电媒质中传播时，电场和磁场的振幅将随传播距离的增加而按指数规律
—６２—
，且磁场强度的相位 电场强度的相位。（每空１分，电子科技大学２００８）
５．在良导体中，电磁波的趋肤深度δ随频率ｆ按 变化。（每空１分，电子科技大学２００９）
６频率为１５０ＭＨｚ的均匀平面波在损耗媒质中传播，已知εｒ＝２．２５、μｒ＝１及
σ
ωε
＝１０－４，当均匀平
面波电磁波在该媒质中传播 ｍ时，其相位改变１８０°。（每空２分，电子科技大学２０１０）
７．频率为ｆ＝１０ＭＨｚ的均匀平面波在海水（ε＝８１ε０、μ＝μ０、σ＝４）中传播时，其趋肤深度为
ｍ，且磁场强度与电场强度的相位差为 。（每空２分，电子科技大学２０１０）
９．良导体是电导率σ１的导电媒质。（　　）（１分，电子科技大学２００９）
１０．电磁波进入导电率不为零的介质时，其振幅将随电磁波进入的深度减小。（　　）（１分，电子
科技大学２００７）
１１．以下关于在导电媒质中传播的电磁波的叙述中，正确的是（　　）。（每题２分，电子科技大学
２００７）
Ａ．不再是平面波 Ｂ．电场和磁场不同相位 Ｃ．振幅不变
１３．穿透深度（或趋肤深度）δ与频率 ｆ及媒质参数（电导率为 σ、磁导率为 μ）的关系是（　　）。
（每题２分，电子科技大学２００６）
Ａ．δ＝πｆμσ Ｂ．δ＝ πｆ槡 μσ Ｃ． １
πｆ槡 μσ
１４．在无界理想媒质中传播的均匀平面电磁波，电场与磁场的相位 （Ａ．相同；Ｂ．不同），
幅度随传播的距离的增加而 （Ａ．不变；Ｂ．衰减）。而在导电媒质中传播的均匀平面波，电场
和磁场的相位 （Ａ．相同；Ｂ．不同），幅度随传播距离的增加 （Ａ．不变；Ｂ．衰减）。（每
空２分，南京理工大学２００８）
１５．电磁波的传播速度随频率变化的现象称为色散效应。理想介质是 （Ａ．非色散媒质；
Ｂ．色散媒质）；导电媒质是 （Ａ．非色散媒质；Ｂ．色散媒质）。
１７．在良导体中，电磁波的趋肤效应随着频率的增加而 （Ａ．减小Ｂ．增大）；随着电导率和
磁导率的增加而 （Ａ．减小Ｂ．增大）。（每空２分，南京理工大学２０１１）
１９．什么是电磁波的色散特性？分析电磁波在导电媒质中的色散特性与在金属波导中的色散有
何不同。（１０分，电子科技大学２０１１）
２０．１ＫＨｚ的均匀平面波在海水（σ＝４Ｓ／ｍ，εｒ＝８１）中传播了３个透入深度的距离时，大约衰减到
原来的百分之几？（９分，北方交通大学２００４）
二、电磁波极化
１．两个同频同方向传播、极化方向互相垂直的线极化波的合成波为圆极化波，则它们的振幅
、相位差为 。（每空１分，电子科技大学２００２、２００５）
８．有一沿正Ｚ轴方向传播的均匀平面波，其电场的复振幅为→ ( )Ｅｚ＝（→ｅｘＥｘ０＋
→ｅｙｊＥｙ０）ｅ
－ｊｋｚ，式中Ｅｘ０
和Ｅｙ０均为实常数。
—７２—
谢处方、饶克谨《电磁场与电磁波》名校真题解析及典型题精讲精练
（１）试分，电子科技大学２０１０析此平面波的极化情况；
（２）当 Ｅｘ０ ≠ Ｅｙ０ 时，此平面波分，电子科技大学２０１０解为两个旋向相反的圆极化波。（１５分，
电子科技大学２０１０）
１３．证明任意一个线极化被可以分，南京理工大学２０１０解为两个幅度相同旋向相反的圆极化波。
（２０分，南京理工大学２０１０）
１０．判断下列波的极化情况（如果是圆极化或椭圆极化请说明是左旋还是右旋）（共１５分，南京理
工大学２０１１，每小题５分）
（１）Ｅ
→
（ｚ）＝（ｅ
→
ｘ－ｊｅ
→
ｙ）Ｅｍｅ
ｊπｚ
（２）Ｅ
→
＝ｅ
→
ｘ０．５ｃｏｓ（１０
８πｔ－２π３ｙ）－ｅ
→
ｚ０．５ｓｉｎ（１０
８πｔ－２π３ｙ）
（３）Ｅ
→
（ｒ
→
，ｔ）＝（ｅ
→
ｘ＋２ｅ
→
ｙ＋ｅ
→
ｚ）１０ｃｏｓ（ωｔ＋３ｘ－ｙ－ｚ）
４．平行极化入射是指 ，垂直极化入射是指 。（每空１分，电子科技大学２０１１）
２．两个同频线极化波会产生叠加。若两个波的合成波为圆极化波，则它们的极化方向 ，
传播方向 ；如果两个波的合成波为纯驻波，则它们的极化方向 ，传播方向 。
（每空１分，电子科技大学２００８）
６．均匀平面波Ｅ＝ａ→ ｘＥ０ｓｉｎ（ωｔ－βｚ）＋ａ
→
ｙＥ０ｓｉｎ（ωｔ－βｚ）的极化方式为。（２分，华南京理工大学
２００５）
Ａ．直线极化 Ｂ．圆极化 Ｃ．左旋圆极化
１２．已知真空中均匀平面波的电场强度为：Ｅ＝（４ｅｘ－３ｅｙ＋ｊ５ｅｚ）ｅ
－ｊπ（３ｘ＋４ｙ），求：
（１）平面波的频率和传播方向；
（２）磁场强度；
（３）平面波的极化特性。（２０分，南京理工大学２０１０）
三、反射与透射
１．极化方向既不平行也不垂直于入射面的线极化波由介质ε１以θ入射在介质ε２上，两介质的分，
电子科技大学２００２界面均为无限大平面。当θ＝θｐ（布儒斯特角）时，反射波的特点为 或当
θ＝θｃ（临界角）时，折射波的特为 。（每空１分，电子科技大学２００２）
１４．什么是电磁波的全反射？分析电磁波在两种理想介质分界面上的全反射与在理想导体表面
上的全反射有何不同。（１０分，电子科技大学２０１１）
４７．平行极化平面电磁波自折射率为３的介质斜入射到折射率为１的介质，若发生全透射求入射
波的入射角。（１５分，西安电子科技大学２０１１）
１６．当平面电磁波垂直入射到理想导体平面时，会在导体以外的空间形成驻波，驻波的特点之一
是平均能流密度为零。（　　）（２分，华南京理工大学２００５）
１５．发生全反射时，透射系数Ｔ不一定等于零。（　　）（１分，电子科技大学２００９）
—８２—
１７．当一束无固定极化方向的电磁波以（　　）入射角向边界投入时，其反射波中仅剩下垂直极化
波。（２分，华南京理工大学２００５）
Ａ．临界角 Ｂ．布儒斯特角 Ｃ．折射角
１３．平面波由理想介质１（ε１＝４ε０、μ１＝μ０）斜入射到与理想介质２（ε２＝２ε０、μ２＝μ０）的分界面上，
发生全反射时的临界角θｃ为 ，发生全透射时的布儒斯特角θｂ为 。（每空１分，电子科
技大学２０１１）
１２．平行极化波由空气中入射到与无损耗介质（ε＝３ε０、μ＝μ０、σ＝０）的分界面上，已知入射角θｉ
＝６０°，则反射系数Γ＝ 、折射（透射）系数τ＝ 。（每空２分，电子科技大学２０１０）
１１．某线极化波由空气中斜入射到与无损耗介质（ε＝３ε０、μ＝μ０、σ＝０）的分界平面上。如要使
反射波振幅为零．则入射波的极化方式是 ，入射角叫θｉ＝ 。（每空１分，电子科技大
学２００９）
８．某线极化波由介质ε１斜入射在介质ε２上，两介质的分，电子科技大学２００８界面为无限大平面。
如要使反射波振幅为零，则入射波的极化方式和入射角应该满足的条件分别是 和 。
（每空１分，电子科技大学２００８）
５．均匀平面被斜入射到理想介质分界面（设μ１＝μ２＝μ３）上时，若ε１＝４ε０、ε２＝ε０，则发生全反射的
临界角θｃ＝ ；若ε１＝ε０、ε２＝３ε０，则布儒斯特角θＢ＝ 。（每空１分，电子科技大学２００５）
３．当圆极化波以布儒斯特θＢ入射到两种不同电介质分界面上时，反射波是 极化波，折射
（透射）波是 极化波。（每空１分，电子科技大学２００５）
２４．空气中传播的均匀平面波的电场强度Ｅ＝ｅｙＥ０ｅ
－π ６ｘ＋８( )ｚ。
（１）求此平面波的波长λ和频率ｆ。
（２）当此平面波入射到位于ｚ＝０处的无限大理想导体平面时，求导体表面上的电流密度Ｊｓ。
３２．自由空间的均匀平面波的电场表达式为Ｅ
→
ｘ，( )ｚ＝ ｅ
→
ｘ２＋ｅ
→
ｚＥｚ( )０ ｅ
－ｊπ ３ｘ－４( )ｚＶ／ｍｚ０为待定量。求：
（１）此平面波的频率ｆ；
（２）Ｅｚ０的值；
（３）磁场强度Ｈ
→
ｘ，( )ｚ；
（４）若此平面波斜入射到位于ｚ＝０的无限在理想导体平板上，求导体平板的电流密度 Ｊ
→
ｓ和电荷
密度ρｓ；
４５．电场复矢量振幅为Ｅ（ｒ）＝ａｘ１．５ｅ
－ｊπｚＶ／ｍ的平面电磁波由空气垂直入射到εｒ＝２．２５，μｒ＝１的
无限大理想介质平面（ｚ＝０），试求：
１．反射波磁场强度的振幅Ｈｒｍ；
２．透射波电场强度的振幅Ｅｔｍ；
３．透射波的相位常数ｋ２。（１５分，西安电子科技大学２００８）
—９２—
谢处方、饶克谨《电磁场与电磁波》名校真题解析及典型题精讲精练
２６．ｚ＜０的半空间为空气，ｚ＞０的半空间为理想介质（ε＝εｒε０、μ＝μ０、σ＝０），当均匀平面波从空
气中垂直入射到介质表面上时，在空气中ｚ＝－０．２５ｍ处测得合成波电场振幅最大值→Ｅｍａｘ＝１０Ｖ／ｍ，
在空气中ｚ＝－０．５ｍ处测得合成波电场振幅最小值→Ｅｍｉｎ＝５Ｖ／ｍ。试求电磁波的频率 ｆ和介质的相
对介电常数εｒ。（１５分，电子科技大学２００６）
２９．ｚ＜Ｏ的半空间为空气，ｚ＞Ｏ的半空间为理想介质（ε＝εｒε０、μ＝μ０、σ＝０），当电场振幅为Ｅｉｍ
＝１０Ｖ／ｍ的均匀平面波从空气中垂直入射到介质表面上时，在空气中距介质表面０．５ｍ处测到合成
波电场振幅的第一个最大值点，且 Ｅ１ ＝１２Ｖ／ｍ。
（１）求电磁波的频率ｆ和介质的相对介电常数εｒ；
（２）空气中的驻波比；
（３）求反射波的平均能流密度Ｓｒａｖ和透射波的平均能流密度Ｓｔａｖ。（１６分，电子科技大学２００８）
４８．如图３所示，假设当真空中一平面电磁波垂直入射到理想介质（μγ＝１）的表面上时，有２５％的
功率被反射回去，已知入射电场振幅为１００Ｖ／ｍ，波长为０．３ｍ。求：
（１）该电介质的相对介电常数εｒ和相位常数Ｋ２；
（２）反射波电磁场复数表达式；
（３）折射波电磁场瞬时表达式；
（４）空气中总的电磁场复数表达式；
（５）透过电介质表面单位面积的功率。（２５分，西北工业大学２００７）
３９．均匀平面波从波阻抗为η１的无耗媒介质中垂直入射至另一种波阻抗为 η２的无耗媒介质平
面上，证明两种媒介质中平均功率密度相等。（１５分，南京理工大学２０１１）
注：ε０＝
１
３６π
×１０－９Ｆ／ｍ　　μ０＝４π×１０
－７Ｈ／ｍ
３６．一均匀平面波在空气中沿 ＋ｚ方向传播，从理想媒质 ε１，μ( )１ 中垂直投射于另一理想媒质
ε２，μ( )２ 上，η１和η２分，南京理工大学２００７别为两种理想媒质的本征阻抗，且η１＞η２，入射磁场为 Ｈ
( )ｚ＝ｅｘＨｍ１０ｅ
－ｊ８ｚＶ／ｍ，求两种理想媒质分，南京理工大学２００７界面上的反射系数与透射系数、反射波
与透射波的电场，并求出在什么情况下反射系数与透射系数绝对值相等。（１５分，南京理工大学
２００７）
４２．电场复矢量振幅为Ｅｉ（ｒ）＝５（ａｘ－ｊａｙ）ｅ
－ｊπｚＶ／ｍ的均匀平面电磁波由 μｒ＝１，εｒ＝９的理想介
质垂直入射向空气，若界面为ｚ＝Ｏ的平面，
（１）试说明入射波的极化状态；
（２）试求反射波电场的复矢量振幅Ｅｒ（ｒ）；
（３）试求当入射角θｉ为何值时反射波为线极化波；
（４）试求当入射角叹为何值时进入空气中的平均功率的Ｚ分量为零。（１５分，西安电子科技大学
２００６）
—０３—
２５．已知某电磁波电场为Ｅ＝ｅｙＥ０ｓｉｎωｔ－( )ｋｚ，其中Ｅ０和ｋ均为实常数。
（１）简要说明此电磁波及其传播媒介的主要特点；
（２）写出电场的复数表达式；
（３）当此波入射到位于ｚ＝０平面上的理想导体板上时，求导体面上的电流密度ＪＳ。（１５分）
２７．均匀平面波从空气中垂直入射到位于 Ｚ＝０处的理想导体平面上，已知入射波电场强度为→Ｅｉ
( )ｚ＝（→ｅｘ－
→ｅｙｊ）Ｅｍｅ
－ｊβ０ｚＶ／ｍ，试求：
（１）入射波的极化状态；
（２）反射波→Ｅｒ（ｚ，ｔ）和复数表示式
→Ｅｒ（ｚ），并说明反射波的极化状态；
（３）反射波→Ｈｒ（ｚ，ｔ）和复数表示式
→Ｈｒ（ｚ）。（１５分，电子科技大学２００６）
２８．空气中有一正弦均匀平面波，其电场强度的复数形式为Ｅ＝ａｘＥ０ｅ
－ｊｋｚ。求：
（１）磁场强度Ｈ；
（２）能流密度Ｓ和平均能流密度Ｓ；
（３）当此波与另一个均匀平面波Ｅ＝ａｙｊＥ０ｅ
－ｊｋｚ叠加时，其合成波的极化特性；
（４）当合成波入射到位于 ｚ＝Ｏ平面上的理想导体板上时反射波的极化特性。（２０分，电子科技
大学２００７）
３８．一均匀平面波沿＋Ｚ方向传播，其电场矢量强度为Ｅ
→
ｉ＝ｅ
→
ｘ１５０ｓｉｎ（ωｔ－βｚ）－ｅ
→
ｚ２５０ｃｏｓ（ωｔ－βｚ）
Ｖ／ｍ。
（１）求相伴的磁场强度ｔ；
（２）若在传播方向上Ｚ＝０处，放置一无限大的理想导体平板，求区域 ｚ＜０中的电场强度和磁场
强度；
（３）求理想导体板表面的电流密度。（２０分，南京理工大学２０１１）
４０．空气中，一沿＋Ｚ方向传播的均匀平面波垂直入射到Ｚ＝０处的理想导体平面上，其入射波的
电场强度为：Ｅｉ＝ｅｘＥｘ０ｃｏｓ（ωｔ－βｚ）＋ｅｙＥｙ０ｓｉｎ（ωｔ－βｚ）Ｖ／ｍ
（１）写出入射波的电场复矢量；
（２）写出入射波磁场的复矢量与瞬时矢量表达式；
（３）入射波，反射波和透射波的平均能流密度；
（４）写出ｚ＜０空间中合成波的电场和磁场的复矢量及理想导体平面上的面电流密度。（２０分，
南京理工大学２０１０）
３５．一个线极化的均匀平面波，从空气垂直入射到一个无穷大铜板表面（该铜板位于 ＸＯＹ平面）。
已知铜板表面入射波电场复振幅为１０３ｅｊ
π
２（Ｖ／ｍ），铜的电导率为 ５．８×１０７（Ｓ／ｍ），相对磁导率为
１。求：
（１）当入射波频率为１００Ｈｚ时，透射波振幅衰减到只有表面值得－１００ｄＢ时所对应的入射深度。
（２）这块铜板单位面积所吸收的平均功率。（１０分，华中科技大学２００６）
—１３—
谢处方、饶克谨《电磁场与电磁波》名校真题解析及典型题精讲精练
第八章　导行电磁波
１．简述均匀波导中的电磁波具有什么传播特点，什么是波导的主模，什么是单模传输；在 ａ×ｂ（ａ
＞２ｂ）的矩形波导中，怎样才能实现单模传输。（１０分，电子科大２００８）
２．试说明为什么矩形波导中不能传输ＴＥＭ被。试列举一个能传输ＴＥＭ波的导波系统。（１０分，
电子科大２００９）
３．矩形波导是一个沿Ｚ轴方向无限长的导体腔，波导中电磁波的传播特性由ｅ－ｉωｔ－γｚ决定，其中 γ
＝２ 槡π με ｆｃ
２－ｆ槡
２，式中的ｆ为电磁波的频率，ｆｃ为波导的截止频率，它与波导的结构有关。分析 ｆ取
不同值时波导中电磁波的传播特性。（１０分，电子科大２０１０）
４．一段两端面封闭的圆柱形空腔，腔内为空气，腔壁及两端面为理想导体，腔体的轴线与 Ｚ轴重
合，两端面分别位于Ｚ＝Ｏ及Ｚ＝Ｌ处。若腔中磁场强度为：Ｈ＝ａφ
Ｈ０
ｒｃｏｓｋｚｃｏｓωｔ
求：（１）Ｅ及ｋ；
（２）两端面内表面上Ｊｓ。（２０分，华中科技２００６）
注意：
!
×Ｈ＝
ａｒ
ｒ ａ→ φ
ａｚ
ｒ

ｒ

φ

ｚ
Ｈｒ ｒＨφ Ｈｚ
—２３—
第九章　电磁辐射
１．已知在体积Ｖ中存在随时间ｔ变化的电荷分布ρ（ｒ，ｔ），它在空间任意点ｒ产生的标量位可表示
为 ｒ，( )ｔ＝ １
４πε０
∫
Ｖ
ρ（ｒ′，ｔ－Ｒｃ）
Ｒ ｄＶ，其中Ｒ＝ ｒ－ｒ′为场点ｒ到源点ｒ′的距离，Ｃ为光速。叙述这个表示
式的物理意义。（１０分，电子科大２００３，电子科大２００７）
２．自由空间中原点处的源（ρ或Ｊ）在ｔ时刻发生变化，此变化将在时刻影响到ｒ处的位函数（φ或
Ａ），也就是说源在时间上 于场（位函数），二者的时间差为 。（每空１分，电子科大
２００２）
３．自由空间中原点处的源（ρ或Ｊ）在ｔ时刻发生变化，此变化将在 时刻影响到 ｒ处的位
函数（φ或Ａ）。（每空１分，电子科大２００５）
４．写出电偶极子辐射场（远区场）的方向图因子，分别画出其 Ｅ面方向图和 Ｈ面方向图，并说明
其特点。（１０分，电子科大２００３、２００７、２０１０）
５．简述电偶极子辐射的远区场具有什么特点。（１０分，电子科大２００８）
６．判断电偶极子的电磁场属于近区、远区的条件分别是：当 时，为近区；当 时，
为远区。（每空１分，电子科大２００５、２００８）
７．电偶极子的远区辐射场是（　　）。（单选２分，电子科大２００６、２００７）
Ａ．非均匀平面波 Ｂ．非均匀球面波 Ｃ．均匀球面波
８．球坐标系中，电偶极子辐射场（远场）的空间分布与距离 ｒ的关系是 ，与俯仰角 θ的关
系是 ，而在ｚ＝０的平面上辐射场的分布为 。（每空１分，电子科大２００２、２００９）
９．在球坐标系中，沿Ｚ方向的电偶极子的辐射场（远区场）在θ＝ 方向上辐射场最大，在
θ＝ 方向上辐射场最小。（每空１分，电子科大２００５、２０１１）
１０．球坐标系中，沿ｚ方向电偶极子的辐射场（远区场）空间分布与坐标ｒ关系为 、与坐标
θ关系为 。（每空１分，电子科大２００５）
１１．同一频率的电磁波，在以下三种媒质中传播时，其波长最长的是（　　）。（２分，华南理工
２００５）
Ａ．理想导体 Ｂ．理想介质 Ｃ．真空
１２．圆形载流线圈在远处一点的磁场相当于一个磁偶极子的磁场。（　　）（２分，华南理工２００５）
１３．已知某天线的辐射功率为１００Ｗ，方向性系数 Ｄ＝３，求：Ｒ＝１０Ｋｍ最大辐射方向的电场强度
—３３—
谢处方、饶克谨《电磁场与电磁波》名校真题解析及典型题精讲精练
振幅。
１４．两个电偶极子相互垂直放置，如图４所示，并以振幅相等、相位相差９００的电流馈电（Ｉ２＝
ｊＩ１），求：
（１）该系统的远区辐射电场强度和磁场强度；
（２）辐射功率；
（３）在θ＝９００，φ＝９００方向上的辐射功率密度。（２０分，西工大２００７）
—４３—