概要信息：

目　录
第一章　信号与系统 （２）
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
第二章　连续系统的时域分析 （９）
!!!!!!!!!!!!!!!!!!!!!!!!!!!!
第三章　离散系统的时域分析 （１２）
!!!!!!!!!!!!!!!!!!!!!!!!!!!
第四章　傅里叶变换和系统的频域分析 （１８）
!!!!!!!!!!!!!!!!!!!!!!!
第五章　复频域分析 （２９）
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
第六章　离散系统的Ｚ域分析 （３８）
!!!!!!!!!!!!!!!!!!!!!!!!!!!
第七章　系统函数 （４５）
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
第八章　系统的状态变量分析 （５３）
!!!!!!!!!!!!!!!!!!!!!!!!!!!
一、教材分析说明
１．信号与线性网络分析　１９８０年６月人民教育出版社
２．信号与线性系统分析（二版）　１９８６年３月高等教育出版社
３．信号与线性系统分析（三版）　１９９８年１０月高等教育出版社
４．信号与线性系统分析（四版）　２００５年８月高等教育出版社
二、辅导课阶段安排
１．教材重点，难点，考点的精讲
２．名校考研真题及典型题的分类解析
３．课程前后内容的整体串讲及模拟试题分析
三、教材内容
第一章　信号与系统
第二章　连续系统的时域分析
第三章　离散系统的时域分析
第四章　傅里叶变换和系统的频域分析
第五章　连续系统的Ｓ域分析
第六章　离散系统的Ｚ域分析
第七章　系统函数
第八章　系统的状态变量分析
—１—
吴大正《信号与线性系统分析》考点精讲
第一章　信号与系统
本章重点框架图
一、信号
１．周期信号的判别及周期Ｔ的计算
①连续信号
②{ 离散信号
２．连续基本信号
①单位阶跃函数
②{ 单位冲击函数
３．离散基本序列
①单位阶跃序列
②{ 单位序列
４．信号的运算
①时移
②反折
③
{













尺度变换
二、系统
１．系统的描述
２．系统的分类
线性系统
时不变系统
因果系统







{
稳定系统
一、信号
信号
连续时间信号
确定信号
周期信号{非周期信号{
随机信号{
离散时间信号
１．周期信号的判别及周期Ｔ的计算
①连续信号
若ｆ１（ｔ），ｆ２（ｔ）是周期为Ｔ１，Ｔ２的周期信号，则当
Ｔ１
Ｔ２
为有理数时，ｆ１（ｔ）＋ｆ２（ｔ）为周期信号，且周期
Ｔ为Ｔ１与Ｔ２的最小公倍数
若
Ｔ１
Ｔ２
＝α
β
，则Ｔ＝αＴ２ ＝βＴ１（α，β为整数）
—２—
【例】　正弦函数ｓｉｎ（ω０ｔ＋φ）一定是周期信号，Ｔ＝
２π
ω０
，而正弦信号的和不一定是周期信号．
②离散信号
若ｆ１（ｋ），ｆ２（ｋ）为周期分别为Ｎ１，Ｎ２的周期序列，则ｆ１（ｋ）＋ｆ２（ｋ），一定是周期序列，这是因为
Ｎ１
Ｎ２
一定为有理数，ｆ１（ｋ）＋ｆ２（ｋ）的周期Ｎ为Ｎ１，Ｎ２的最小公倍数。
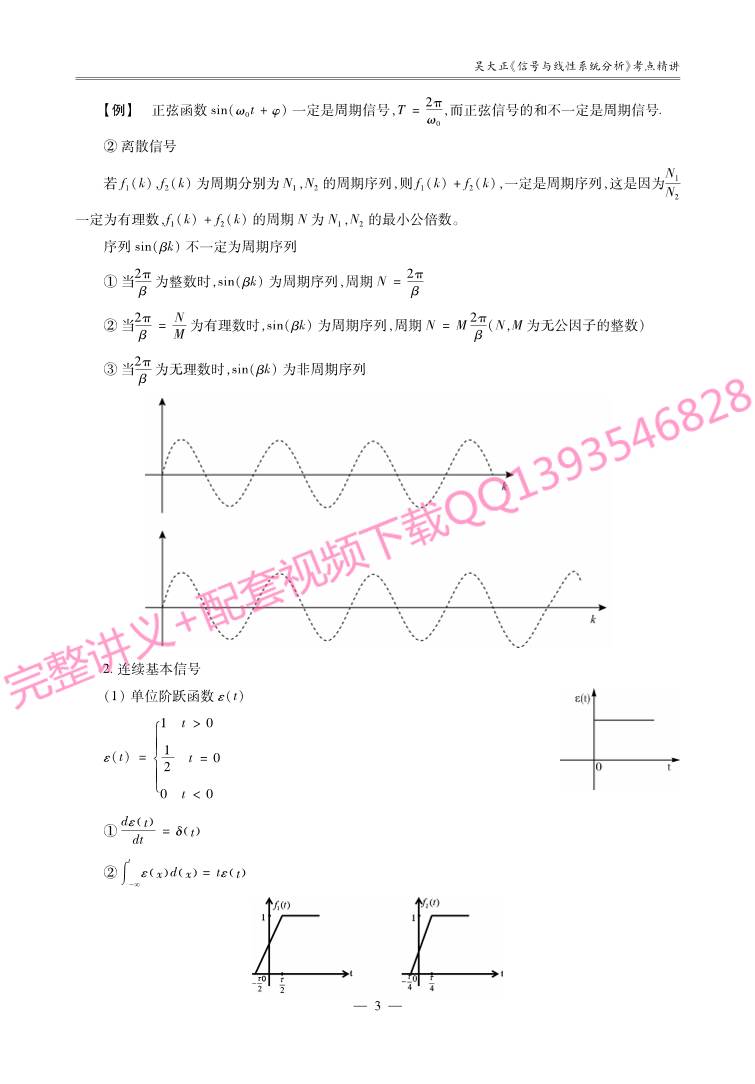
序列ｓｉｎ（βｋ）不一定为周期序列
①当２πβ
为整数时，ｓｉｎ（βｋ）为周期序列，周期Ｎ＝２πβ
②当２πβ
＝ＮＭ为有理数时，ｓｉｎ（βｋ）为周期序列，周期Ｎ＝Ｍ
２π
β
（Ｎ，Ｍ为无公因子的整数）
③当２πβ
为无理数时，ｓｉｎ（βｋ）为非周期序列
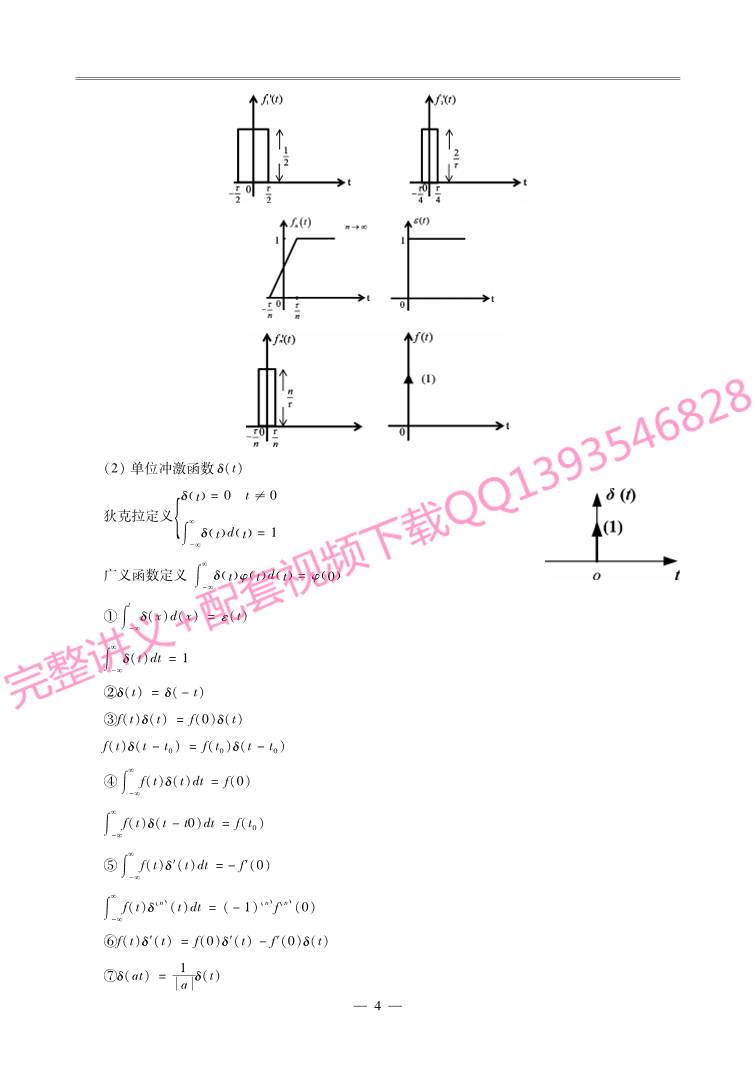
２．连续基本信号
（１）单位阶跃函数ε（ｔ）
ε（ｔ）＝
１　ｔ＞０
１
２　ｔ＝０
０　ｔ＜





０
①
ｄε( )ｔ
ｄｔ ＝δ( )ｔ
②∫
ｔ
－
!
ε( )ｘｄ( )ｘ＝ｔε( )ｔ
—３—
吴大正《信号与线性系统分析》考点精讲
（２）单位冲激函数δ（ｔ）
狄克拉定义
δ( )ｔ＝０　ｔ≠０
∫
!
－
!
δ( )ｔｄ( )ｔ＝{ １
广义函数定义：∫
!
－
!
δ( )ｔφ( )ｔｄ( )ｔ＝φ( )０
①∫
ｔ
－
!
δ（ｘ）ｄ（ｘ）＝ε（ｔ）
∫
!
－
!
δ（ｔ）ｄｔ＝１
②δ（ｔ）＝δ（－ｔ）
③ｆ（ｔ）δ（ｔ）＝ｆ（０）δ（ｔ）
ｆ（ｔ）δ（ｔ－ｔ０）＝ｆ（ｔ０）δ（ｔ－ｔ０）
④∫
!
－
!
ｆ（ｔ）δ（ｔ）ｄｔ＝ｆ（０）
∫
!
－
!
ｆ（ｔ）δ（ｔ－ｔ０）ｄｔ＝ｆ（ｔ０）
⑤∫
!
－
!
ｆ（ｔ）δ′（ｔ）ｄｔ＝－ｆ′（０）
∫
!
－
!
ｆ（ｔ）δ（ｎ）（ｔ）ｄｔ＝（－１）（ｎ）ｆ（ｎ）（０）
⑥ｆ（ｔ）δ′（ｔ）＝ｆ（０）δ′（ｔ）－ｆ′（０）δ（ｔ）
⑦δ（ａｔ）＝ １
ａδ（ｔ）
—４—
⑧δ′（ａｔ）＝ １
ａ
１
ａδ′（ｔ）
δ（ｎ）（ａｔ）＝ １
ａ
１
ａｎ
δ（ｎ）（ｔ）
⑨δｆ（ｔ[ ]） ＝∑
ｎ
ｉ＝１
１
ｆ′（ｔｉ）
δ（ｔ－ｔｉ）
ｆ（ｔ）＝０在ｔｉ有单根（ｉ＝１，２，３，…，ｎ[ ]）
３．离散基本序列
（１）单位阶跃序列
ε（ｋ）＝
１　ｋ≥０
０　ｋ＜{ ０
　　　　
（２）单位序列
δ（ｋ）＝
１　ｋ＝０
０　ｋ≠{ ０
①ｆ( )ｋδ( )ｋ＝ｆ（０）δ( )ｋ
②ｆ( )ｋδ( )ｋ－ｉ＝ｆ( )ｉδ( )ｋ－ｉ
③δ( )ｋ＝ε( )ｋ－εｋ－( )１
④ε( )ｋ＝∑
ｋ
ｉ＝－
!
δ( )ｉ＝∑
!
ｉ＝０
δ( )ｋ－ｉ
４．信号的运算。
①时移
ｆ（ｔ →） ｆ（ｔ
!
ｔ０）
②反折
ｆ（ｔ →） ｆ（－ｔ）
若ｔ０ ＞０图形右移ｔ０
③尺度变换
ｆ（ｔ →） ｆ（ａｔ）
｜ａ｜＞１　ｆ（ｔ）在ｔ轴压缩到１ａ
｜ａ｜＜１　ｆ（ｔ）在ｔ轴扩展到（１ａ）倍
—５—
吴大正《信号与线性系统分析》考点精讲
【例１】
【例２】
【例３】
—６—
【例４】
二、系统
１．系统的描述
连续系统 离散系统
数学方程 微分方程 差分方程
系统函数
Ｈ（ｓ）
Ｈ（ｊω）
Ｈ（ｚ）
Ｈ（ｅｊθ）
状态空间描述 ｘ
·
＝Ａｘ＋Ｂｆ
ｙ＝Ｃｘ＋Ｄｆ
ｘ（ｋ＋１）＝Ａｘ（ｋ）＋Ｂｆ（ｋ）
ｙ（ｋ）＝Ｃｘ（ｋ）＋Ｄｆ（ｋ）
２．系统的分类
①线性系统
②时不变系统
③因果系统
④稳定系统
（１）线性系统
①分解性
②零输入线性
③零状态线性
（２）时不变系统
　ｆ（ｔ）
→
　
→　０　 ｙｚｓ（ｔ）
ｆ（ｔ →） ｙｚｓ（ｔ）
ｆ（ｔ－ｔ０ →） ｙｚｓ（ｔ－ｔ０）
线性时不变系统为线性常系数微分方程
（３）因果系统
　ｆ（ｔ）
→
　
→　０　 ｙｚｓ（ｔ）
—７—
吴大正《信号与线性系统分析》考点精讲
若ｔ＜０　ｆ（ｔ）＝０
则ｔ＜０　ｙｚｓ（ｔ）＝０
（４）稳定系统
　ｆ（ｔ）
→
　
→　０　 ｙｚｓ（ｔ）
若 ｆ（ｔ）≤Ｍ１，则有 ｙｚｓ（ｔ）≤Ｍ２　 －!
＜ｔ＜
!
离散系统的分类与上述类似
【例】　判定下列系统是线性、时不变、因果、稳定中的哪个．
①ｙ( )ｔ＝ｅ－２ｔｘ( )０＋∫
ｔ
０
ｓｉｎｘｆ( )ｘｄｘ
②ｙ( )ｔ＝ｆ（ｔ）ｘ( )０＋∫
ｔ
０
ｆ( )ｘｄｘ
③ｙ( )ｋ＝ ０．( )５ｋｘ( )０＋ｆ( )ｋｆ( )ｋ－ｚ
④ｙ( )ｔ＝ｅ－ｋｘ( )０＋∑
ｋ
ｉ＝０
ｆ( )ｉ
⑤ｙ( )ｔ＝ｅ－ｔｘ( )０＋ｆ（ｔ＋１）
⑥ｙ( )ｔ＝２ｘ( )０＋ ｆ( )ｔ
⑦ｙ( )ｔ＝２－ｋｘ( )０＋ ｋ－( )２ｆ( )ｋ
⑧ｙ′( )ｔ＋４ｙ′( )ｔ＋３ｙ( )ｔ＝２ｆ（ｔ）＋３
⑨ｙ″( )ｔ＋ｙ′( )ｔ＋ｙ( )ｔ＝２ｆ（１－ｔ）
—８—
第二章 　 连续系统的时域分析
本章重点框架图：
连续系统的时域分析
ＬＴＩ系统的响应
①经典解
②{ 卷积解
冲激响应ｈ（ｔ）





卷积积分
一、ＬＴＩ系统的响应
１．经典解
ｙ（ｔ）＝ｙｈ（ｔ）＋ｙＰ（ｔ）
特解ｙＰ（ｔ）与ｆ（ｔ）有关，对于大量的ｆ（ｔ），ｙＰ（ｔ）
无法确定，可知经典法的应用范围很有限
２．卷积解
ｙ（ｔ）＝ｙｚｉ（ｔ）＋ｙｚｓ（ｔ）
（１）零输入解ｙｚｉ（ｔ）
　
→
０　
　ｘ０ →　 ｙｚｉ（ｔ）
（２）零状态解ｙｚｓ（ｔ）
　ｆ（ｔ）
→
　
→　０　 ｙｚｓ（ｔ）
①ｆ（ｔ）表示为一系列基本信号的和
ｆ（ｔ）＝∫
!
－
!
ｆ（τ）δ（ｔ－τ）ｄτ
②基本信号的响应
　δ（ｔ）　
　ε（ｔ）
→
　
→　０　
ｈ（ｔ）
ｇ（ｔ）
③迭加求和
ｙｚｓ（ｔ）＝∫
!
－
!
ｆ（τ）ｈ（ｔ－τ）ｄτ
（１）因果系统
—９—
吴大正《信号与线性系统分析》考点精讲
ｘ＜０　ｈ（ｔ）＝０
ｙｚｓ（ｔ）＝∫
ｔ
－
!
ｆ（τ）ｈ（ｔ－τ）ｄτ
（２）有始信号
ｔ＜０　ｆ（ｔ）＝０
ｙｚｓ（ｔ）＝∫
ｔ
０
ｆ（τ）ｈ（ｔ－τ）ｄτ
二、冲激响应ｈ（ｔ）
冲激响应ｈ（ｔ）
　ｆ（ｔ）　
　δ（ｔ）
→
　
→　０　
ｙｚｓ（ｔ）
ｈ（ｔ）
１．ｈ″( )ｔ＋ａ１ｈ′( )ｔ＋ａ０ｈ( )ｔ＝δ( )ｔ
ｔ０　ｈ（０－）＝ｈ′（０－）＝０
一般情况：
ｔ０　ｈ( )ｎ ( )ｔ＋ａｎ－１ｈｎ－( )１ ( )ｔ＋… ＋ａ１ｈ′( )ｔ＋ａ０ｈ( )ｔ＝δ( )ｔ
ｈ（０－）＝ｈ′（０－）＝… ＝ｈｎ－( )１（０－）＝０
则有：
ｈｎ－( )１（０＋）＝１
ｈｎ－( )２（０＋）＝… ＝ｈ′（０＋）＝ｈ（０＋）＝０
２．ｔ０
ｈ（ｎ）（ｔ）＋ａｎ－１ｈ
（ｎ－１）（ｔ）＋… ＋ａ１ｈ′（ｔ）＋ａ０ｈ（ｔ）
＝ｂｍδ
（ｍ）（ｔ）＋ｂｍ－１δ
（ｍ－１）（ｔ）＋… ＋ｂ１δ′（ｔ）＋ｂ０δ（ｔ）
（１）先求ｈ（ｎ）１ （ｔ）＋ａｎ－１ｈ
（ｎ－１）
１ （ｔ）＋… ＋ａ１ｈ′１（ｔ）＋ａ０ｈ１（ｔ）＝δ（ｔ）
得到ｈ１（ｔ）
（２）应用迭加：
ｈ（ｔ）＝ｂｍｈ１
（ｍ）（ｔ）＋ｂｍ－１ｈ１
（ｍ－１）（ｔ）＋… ＋ｂ１ｈ１′（ｔ）＋ｂ０ｈ１（ｔ）
三、卷积积分
１．定义
ｆ１（ｔ）ｆ２（ｔ）＝∫
!
－
!
ｆ１（τ）ｆ２（ｔ－τ）ｄτ
２．几何意义
３．性质
①交换律
ｆ１（ｔ）ｆ２（ｔ）＝ｆ２（ｔ）ｆ１（ｔ）
—０１—
②结合律
ｆ１（ｔ）ｆ２（ｔ[ ]）ｆ３（ｔ）＝ｆ１（ｔ） ｆ２（ｔ）ｆ３（ｔ[ ]）
③分配律
ｆ１（ｔ） ｆ２（ｔ）＋ｆ３（ｔ[ ]） ＝ｆ１（ｔ）ｆ２（ｔ）＋ｆ１（ｔ）ｆ３（ｔ）
④时移
若：ｆ１（ｔ）ｆ２（ｔ）＝ｆ( )ｔ
则ｆ１（ｔ－ｔ０）ｆ２（ｔ）＝ｆｔ－ｔ( )
０
⑤微分
ｄ
ｄｔｆ１（ｔ）ｆ２（ｔ
[ ]） ＝
ｄｆ１（ｔ）
ｄｔｆ２（ｔ）＝ｆ１（ｔ）
ｄｆ２（ｔ）
ｄｔ
⑥积分
∫
ｔ
－
!
ｆ１（ｔ）ｆ２（ｔ）ｄｔ＝∫
ｔ
－
!
ｆ１（ｘ）ｄｘｆ２（ｔ）＝ｆ１（ｔ）∫
ｔ
－
!
ｆ２（ｘ）ｄｘ
从而有：
ｆ１（ｔ）ｆ２（ｔ）＝∫
ｔ
－
!
ｆ１（ｘ）ｄｘ
ｄｆ２（ｔ）
ｄｔ ＝
ｄｆ１（ｔ）
ｄｔ∫
ｔ
－
!
ｆ２（ｘ）ｄｘ
４．几个特殊的卷积
①ｆ（ｔ）δ（ｔ）＝ｆ（ｔ）
②ｆ（ｔ）δ（ｔ－ｔ０）＝ｆ（ｔ－ｔ０）
③ｆ（ｔ）δ′（ｔ）＝ｆ′（ｔ）
④ｆ（ｔ）ε（ｔ）＝∫
ｔ
－
!
ｆ（ｘ）ｄｘ
⑤ｆ（ｔ）ｋ＝ｋ∫
!
－
!
ｆ（τ）ｄτ（ｋ为常数）
四、卷积积分的计算
１．按定义求
２．图解法
３．利用性质
—１１—
吴大正《信号与线性系统分析》考点精讲
第三章 　 离散系统的时域分析
本章重点框架图
一、差分方程及经典解
二、ｙ（ｋ）＝ｙｚｉ（ｋ）＋ｙｚｓ（ｋ）
三、单位响应ｈ（ｋ）
四、卷积和
一、差分方程及经典解
１．差分方程
　ｆ（ｋ）
→
　
　ｘ（０） →　 ｙ（ｋ）
ｙ（ｋ）与ｆ（ｋ）之间的数学方程为差分方程
（１）差分
前向差分Δｆ( )ｋ＝ｆｋ＋( )１－ｆ( )ｋ
后向差分
"
ｆ( )ｋ＝ｆ( )ｋ－ｆｋ－( )１
二阶差分
"
２ｆ( )ｋ＝"
"
ｆ( )[ ]ｋ
＝
" ｆ( )ｋ－ｆｋ－( )[ ]１
＝
"
ｆ( )ｋ－"
ｆｋ－( )１
＝ｆ( )ｋ－ｆｋ－( )１－ ｆｋ－( )１－ｆｋ－( )[ ]２
＝ｆ( )ｋ－２ｆｋ－( )１＋ｆｋ－( )２
（２）差分方程
【例】　银行存款
每月存入ｆ( )ｋ元( )前一时存入 利息β元 ／元，月按照复息计，试求：一年的本利为多少元
设第ｋ个月月初的本利为ｙ( )ｋ元
一般差分方程可写成以下两种形式
①前向差分方程
【例】　ｙｋ＋( )２＋５ｙｋ＋( )１＋６ｙ( )ｋ＝２ｆｋ＋( )１＋ｆ( )ｋ　ｋ０
—２１—
需要条件：ｙ( )０，ｙ( )１
②后向差分方程
【例】　ｙ( )ｋ＋５ｙｋ－( )１＋６ｙｋ－( )２ ＝２ｆｋ－( )１＋ｆｋ－( )２　ｋ０
需要条件：ｙ－( )１，ｙ－( )２
２．差分方程的经典解
ｋ０　ｙ( )ｋ＋ａｎ－１ｙｋ－( )１＋… ＋ａ１ｙｋ－ ｎ＋( )[ ]１ ＋ａ０ｙ( )ｋ－ｎ
＝ｂｍｆ( )ｋ＋… ＋ｂ０ｆ( )ｋ－ｍ
（１）齐次解
ｙｈ( )ｋ＋ａｎ－１ｙｈ ｋ－( )１＋… ＋ａ０ｙｈ( )ｋ－ｎ＝０
特征方程：
１＋ａｎ－１λ
－１＋… ＋ａ０λ
－ｎ ＝０
λｎ＋ａｎ－１λ
ｎ－１＋… ＋ａ０ ＝０
特征根：
λ１，λ２，…，λｎ
①若λｉ为不相等的单根
ｙｈ( )ｋ＝ｃ１λ１
ｋ＋ｃ２λ２
ｋ＋… ＋ｃｎλｎ
ｋ
②若在λ处有ｒ阶重根
ｙｈ( )ｋ＝ ｃ０＋ｃ１ｋ＋… ＋ｃｒｋ
ｒ－( )１ λｋ＋[ ]单根响应
（２）特解ｙｐ( )ｋ
（３）全解
ｙ( )ｋ＝ｙｈ( )ｋ＋ｙｐ( )ｋ
代入初始条件求出系数ｃｉ
【例】　银行存款的问题
若ｆ( )ｋ为任意信号，ｙｐ( )ｋ无法求，可见经典法的应用很有限
二、ｙ( )ｋ＝ｙｚｉ( )ｋ＋ｙｚｓ( )ｋ
　ｆ（ｋ）
→
　
　ｘ（０） →　 ｙ（ｋ）
ｋ０　ｙ( )ｋ＋ａ１ｙｋ－( )１＋ａ０ｙｋ－( )２
＝ｂ１ｆｋ－( )１＋ｂ０ｆｋ－( )２
ｙ－( )１，ｙ－( )２
１．零输入响应
→
　０　
　ｘ（０） →　 ｙｚｉ（ｋ）
—３１—
吴大正《信号与线性系统分析》考点精讲
ｋ０　ｙｚｉ( )ｋ＋ａ１ｙｚｉ ｋ－( )１＋ａ０ｙｚｉ ｋ－( )２
ｙｚｉ －( )１，ｙｚｉ －( )２
ｙｚｉ －( )１ ＝ｙ－( )１，ｙｚｉ －( )２ ＝ｙ－( )２
从概念上来看，应代入ｙｚｉ( )０，ｙｚｉ( )１的条件
例如：ｙ( )ｋ＋
５
６ｙｋ－
( )１＋
１
６ｙｋ－
( )２ ＝ｆ( )ｋ
ｙ－( )１ ＝６，ｙ－( )２ ＝６，ｆ( )ｋ＝ε( )ｋ
求：ｙｚｉ( )ｋ
２．零状态响应
　ｆ（ｋ）
→
　
→　０　 ｙｚｓ（ｋ）
ｋ０　ｙｚｓ( )ｋ＋ａ１ｙｚｓ ｋ－( )１＋ａ０ｙｚｓ ｋ－( )２ ＝ｂ１ｆｋ－( )１＋ｂ０ｆｋ－( )２
ｙｚｓ －( )１ ＝ｙｚｓ －( )２ ＝０
（１）ｆ（ｋ）的分解
（２）单位响应
　δ（ｋ）
→
　
→　０　 ｈ（ｋ）
（３）ｙｚｓ( )ｋ＝ｆ( )ｋｈ( )
→
ｋ
→　０　
δ（ｋ →） ｈ（ｋ）
ｆ( )ｉδ( )ｋ－ｉ→ｆ( )ｉｈ( )ｋ－ｉ
∑
!
ｉ＝－
!
ｆ( )ｉδ( )ｋ－ｉ→∑
!
ｉ＝－
!
ｆ( )ｉｈ( )ｋ－ｉ
三、单位响应ｈ（ｋ）
　δ（ｋ）
→
　
→　０　 ｈ（ｋ）
描述系统的数学方程为：
ｋ０　ｙｚｓ( )ｋ＋ａｎ－１ｙｚｓ ｋ－( )１＋… ＋ａ０ｙｚｓ( )ｋ－ｎ
＝ｂｍｆ( )ｋ＋… ＋ｂ０ｆ( )ｋ－ｍ
ｙｚｓ －( )１ ＝ｙｚｓ －( )２ ＝… ＝ｙｚｓ( )－ｎ＝０
—４１—
求ｈ（ｋ）的方程为：
ｋ０　ｈ( )ｋ＋ａｎ－１ｈｋ－( )１＋…ａ０ｈ( )ｋ－ｎ
＝ｂｍδ( )ｋ＋…ｂ０δ( )ｋ－ｍ
ｈ－( )１ ＝ｈ－( )２ ＝…ｈ( )－ｎ＝０
引入辅助方程
ｋ０　ｈ１( )ｋ＋ａｎ－１ｈ１ ｋ－( )１＋……ａ１ｈ( )ｋ－ｎ＝δ( )ｋ
ｈ１ －( )１ ＝ｈ１ －( )２ ＝…ｈ１( )－ｎ＝０
【例】　系统方程为：
ｋ０　ｙｚｓ( )ｋ＋
１
６ｙｚｓ ｋ－
( )１－
１
６ｙｚｓ ｋ－
( )２ ＝２ｆ( )ｋ－３ｆｋ－( )１，求单位响应ｈ( )ｋ．
【解】　ｋ０　ｈ( )ｋ＋
１
６ｈｋ－
( )１－
１
６ｈｋ－
( )２ ＝２δ( )ｋ－３δｋ－( )１
ｈ－( )１ ＝ｈ－( )２ ＝０
引入辅助方程
ｋ０　ｈ１( )ｋ＋
１
６ｈ１ ｋ－
( )１－
１
６ｈ１ ｋ－
( )２ ＝δ( )ｋ
ｈ１ －( )１ ＝ｈ？１ －( )２ ＝０
四、卷积和
１．定义
ｆ１( )ｋｆ２( )ｋ＝∑
!
ｉ＝－
!
ｆ１( )ｉｆ２( )ｋ－ｉ
若对有始信号ｋ＜０，ｆ１( )ｋ＝０，ｆ２( )ｋ＝０
则ｆ１( )ｋｆ２( )ｋ＝∑
ｋ
ｉ＝０
ｆ１( )ｉｆ２( )ｋ－ｉ
２．性质
（１）交换律
ｆ１( )ｋｆ２( )ｋ＝ｆ２( )ｋｆ１( )ｋ
（２）分配律
ｆ１( )ｋ ｆ２( )ｋ＋ｆ３( )[ ]ｋ ＝ｆ１( )ｋｆ２( )ｋ＋ｆ１( )ｋｆ３( )ｋ
（３）结合律
ｆ１( )ｋｆ２( )[ ]ｋ ｆ３( )ｋ＝ｆ１( )ｋ ｆ２( )ｋｆ３( )[ ]ｋ
（４）位移
若ｆ１( )ｋｆ２( )ｋ＝ｆ( )ｋ
则ｆ１ ｋ－ｋ( )
１ ｆ２ ｋ－ｋ( )
２ ＝ｆｋ－ｋ１－ｋ( )
２
—５１—
吴大正《信号与线性系统分析》考点精讲
３．ｎ个常用的卷积
( )１ｆ( )ｋδ( )ｋ＝ｆ( )ｋ
( )２ｆ( )ｋδｋ－ｋ( )
０ ＝ｆｋ－ｋ( )
０
( )３ε( )ｋε( )ｋ＝ ｋ＋( )１ε( )ｋ
( )４ε( )ｋａｋε( )ｋ＝
１－ａｋ＋１
１－ａε
( )ｋ
４．卷积的求取
（１）图解法
ｆ１( )ｋｆ２( )ｋ＝∑
!
ｉ＝－
!
ｆ１( )ｉｆ２( )ｋ－ｉ
ｆ２( )－ｉ反褶
ｆ２( )ｋ－ｉ位移
ｆ１( )ｉｆ２( )ｋ－ｉ相乘
∑ｆ１( )ｉｆ２( )ｋ－ｉ求和
【例】　ｆ１（ｋ）
１　ｋ＝０，１，２
０　{
其余
，ｆ２（ｋ）
ｋ　ｋ＝０，１，２，３
０　{
其余
（２）利用δ( )ｋ的卷积求
（３）不进位乘法( )有限长序列适用
ｆ( )ｋ＝ｆ１( )ｋｆ１( )ｋ＝∑
!
ｉ＝－
!
ｆ１( )ｉｆ２( )ｋ－ｉ
＝… ＋ｆ１ －( )１ｆ２ ｋ＋( )１＋ｆ１( )０ｆ２( )ｋ＋ｆ１( )１ｆ２ ｋ－( )１
＋… ＋ｆ１( )ｉｆ２( )ｋ－ｉ＋…
ｆ( )ｋ等于所有两序号之和为ｋ的样本乘积之和
（４）按定义求
ｆ１( )ｋｆ２( )ｋ＝∑
!
ｉ＝－
!
ｆ１( )ｉｆ２( )ｋ－ｉ
【例１】　（１）序列和∑
ｋ
ｎ＝－
!
ｓｉｎｎπ４δｎ－
( )２ ＝
（２）εｋ＋( )１δｋ－( )１－εｋ－( )１δ( )ｋ＝ ０，δ( )ｋ，δｋ－( )１，ε( )ｋ，εｋ－( )[ ]１
（３）若ｆ１( )ｋｆ２( )ｋ＝ｆ( )ｋ，则ｆ( )１ ＝ ，ｆ( )２ ＝ ．
—６１—
（４）序列２ｃｏｓ１．５πｋ＋π( )４ 的周期Ｎ＝ ．
【例２】　已知ｙｋ＋( )２＋３ｙｋ＋( )１＋２ｙ( )ｋ＝ｆｋ＋( )１＋ｆ( )ｋ，ｙｚｉ( )０ ＝－０．５，ｙｚｉ( )１ ＝０，ｆ( )ｋ＝
ｅｋε( )ｋ，ｙｚｉ( )ｋ，ｙｚｓ( )ｋ．
【例３】　某离散系统ｙ( )ｋ＝ｆ( )ｋ＋ｅａｙｋ－( )１，求单位响应ｈ( )ｋ及其阶跃响应ｇ( )ｋ．
【例４】　试求ε－ｋ＋( )１ ( )１２
ｋ
ε( )ｋ．
【例５】　求２－ｋε( )－ｋ３－ｋε( )ｋ．
【例６】　描述ＬＴＩ系统数学方程为：
ｋ０　ｙ( )ｋ＋４ｙｋ－( )１＋４ｙｋ－( )２ ＝ｆ( )ｋ－ｆｋ－( )１
ｙ( )０ ＝１，ｙ( )１ ＝２，ｆ( )ｋ＝ε( )ｋ
求：ｙｚｉ( )ｋ及ｙｚｓ( )ｋ
【例７】　已知ｈ１( )ｋ＝ε( )ｋ，ｈ２( )ｋ＝ －( )１ｋε( )ｋ，ｈ３( )ｋ＝δｋ－( )１，ｆ( )ｋ＝ε( )ｋ－εｋ－( )２，求：
ｙｚｓ( )ｋ．
【例８】　已知ｆ( )ｋ如图所示，ｙｚｓ( )ｋ＝２ｋε( )ｋ，试用时域法求系统单位响应ｈ( )ｋ．
—７１—
吴大正《信号与线性系统分析》考点精讲
第四章 　 傅里叶变换和系统的频域分析
本章重点框架图
一、周期信号的分析———傅里叶级数
二、非周期信号的分析———傅里叶变换
三、Ｆ变换的性质
四、频域分析
五、取样定理
一、周期信号的分析———傅里叶级数
１．傅里叶级数的三角形式
ｆ( )ｔ＝
Ａ０
２＋∑
!
ｎ＝１
ＡｎｃｏｓｎΩｔ＋φ( )
ｎ
＝
Ａ０
２＋∑
!
ｎ＝１
Ａｎ ｃｏｓφｎｃｏｓｎΩｔ－ｓｉｎφｎｓｉｎｎΩ[ ]ｔ
＝
ａ０
２＋∑
!
ｎ＝１
ａｎｃｏｓｎΩｔ＋∑
!
ｎ＝１
ｂｎｓｉｎｎΩｔ
Ω ＝２πＴ为基波频率，Ｔ为周期
ａ０ ＝
２
Ｔ∫
Ｔ
２
－Ｔ２
ｆ( )ｔｄ( )ｔ
ａｎ ＝
２
Ｔ∫
Ｔ
２
－Ｔ２
ｆ( )ｔｃｏｓｎΩｔｄ( )ｔ
ｂｎ ＝
２
Ｔ∫
Ｔ
２
－Ｔ２
ｆ( )ｔｓｉｎｎΩｔｄ( )ｔ（ｎ＝１，２，３，…）
（１）
ａｎ ＝Ａｎｃｏｓφｎ
ｂｎ ＝－Ａｎｓｉｎφ
{
ｎ
Ａｎ ＝ ａ２ｎ＋ｂ
２
槡 ｎ
φｎ ＝－ａｒｃｔｇ
ｂｎ
ａ
{
ｎ
—８１—
（２）
ａｎ ＝ａ－ｎ
ｂｎ＝－ｂ{
－ｎ
Ａｎ ＝Ａ－ｎ
φｎ ＝－φ
{
－ｎ
２．傅里叶级数的指数形式
ｆ( )ｔ＝
１
２∑
!
ｎ＝－
!
Ａｎ
·
ｅｊｎΩｔ＝∑
!
ｎ＝－
!
ＦｎｅｊｎΩｔ
其中
Ａｎ
·
＝Ａｎｅｊφｎ ＝２Ｔ∫
Ｔ
２
－Ｔ２
ｆ( )ｔｅ－ｊｎΩｔｄｔ
【例如】　Ｆｎ ＝
１
Ｔ∫
Ｔ
２
－Ｔ２
ｆ（ｔ）ｅ－ｊｎΩｔｄｔ
＝１Ｔ∫
τ
２
－τ２
１·ｅ－ｊｎΩｔｄｔ＝１Ｔ
ｅ－ｊｎΩｔ
－ｊｎΩ
τ
２
－τ２
＝２Ｔ
ｓｉｎ（ｎΩτ２）
ｎΩ
＝τＴ
ｓｉｎｎΩτ２
ｎΩτ
２
令Ｓａ( )ｘ＝ｓｉｎ( )ｘ／ｘ（取样函数）
Ｆｎ ＝
τ
ＴＳａ（
ｎΩτ
２）
Ｆｎ ＝ Ｆｎ ｅ
ｊφｎ
（１）离散性
（２）谐波性
（３）收敛性
３．奇偶性
—９１—
吴大正《信号与线性系统分析》考点精讲
（１）ｆ( )ｔ为偶函数ｆ( )ｔ＝ｆ( )－ｔ
则ｂｎ ＝０，ａｎ ＝
４
Ｔ∫
Ｔ
２
０
ｆ( )ｔｃｏｓｎΩｔｄｔ
Ａｎ
·
＝ａｎ
Ｆｎ ＝
１
２ａｎ
（２）ｆ( )ｔ为奇函数ｆ( )ｔ＝－ｆ( )－ｔ
ａ０ ＝ａｎ ＝０
ｂｎ ＝
４
Ｔ∫
Ｔ
２
０
ｆ( )ｔｓｉｎｎΩｔｄｔ
Ａｎ
·
＝－ｊｂｎ
Ｆｎ ＝－ｊ
１
２ｂｎ
（３）ｆ( )ｔ为奇谐函数ｆ( )ｔ＝－ｆｔ－τ( )２
ｎ只能取奇数，当ｎ取偶数时，ａｎ ＝０，ｂｎ ＝０
４．周期信号的频谱
Ａｎ
·
～ｎΩ的关系曲线———单边谱
Ｆｎ ～ｎΩ的关系曲线———双边谱
【例如】　ｆ（ｔ）＝２＋３ｓｉｎπｔ－６ｃｏｓ（２πｔ－４５°）＋４ｃｏｓ（４πｔ＋３０°）＋２ｓｉｎ（５πｔ＋３０°）
５．信号功率
Ｐ＝１Ｔ∫
Ｔ
２
－Ｔ２
ｆ２( )ｔｄｔ
＝∑
!
－
!
Ｆｎ
２
＝ Ｆ０
２＋２∑
!
ｎ＝１
Ｆｎ
２
二、非周期信号的分析———傅里叶变换
１．定义
Ｆｊ( )ω ＝∫
!
－
!
ｆ( )ｔｅ－ｊωｔｄｔ
ｆ( )ｔ＝
１
２π∫
!
－
!
Ｆｊ( )ωｅｊωｔｄω
频谱密度函数：Ｆｊ( )ω ＝ Ｆｊ( )ω ｅｊφ( )ω
量纲为单位频率的振幅
（１）Ｆｊ( )ω的奇偶性
—０２—
Ｆｊ( )ω ＝ Ｆｊ( )ω ｅｊφ( )ω ＝Ｒ( )ω ＋ｊｘ( )ω
Ｒ( )ω ＝ Ｆｊ( )ω ｃｏｓφ( )ω
ｘ( )ω ＝ Ｆｊ( )ω ｓｉｎφ( )ω
①
Ｒ( )ω ＝Ｒ －( )ω
ｘ( )ω ＝－ｘ－( ){
ω
②
Ｆｊ( )ω ＝ Ｆ －ｊ( )ω
φ( )ω ＝－φ －( ){
ω
【例】　Ｆｊ( )ω ＝∫
τ
２
－τ２
１·ｅ－ｊωｔｄｔ＝τＳａωτ( )２
（２）ｆ( )ｔ的奇偶性
①ｆ( )ｔ＝ｆ( )－ｔ
Ｆｊ( )ω ＝Ｒ( )ω
Ｆｊ( )ω为ω的实函数，而且为ω的偶函数
②ｆ( )ｔ＝－ｆ( )－ｔ
Ｆｊ( )ω ＝ｊｘ( )ω
Ｆｊ( )ω为ω的虚函数，而且为ω的奇函数
２．常用信号的Ｆ（ｊω）
（１）δ( )ｔ１
（２）１２πδ( )ω
（３）δ′( )ｔｊωδ( )ｎ ( )ｔ ｊ( )ω ｎ
（４）ε( )ｔπδ( )ω ＋
１
ｊω
（５）ｇτ( )ｔτＳａωτ( )２
（６）Ｓａ( )ａｔ πａｇ２ａ
( )ω
—１２—
吴大正《信号与线性系统分析》考点精讲
（７）ｓｇｎ( )ｔ
２
ｊω
（８）ｅ－αｔε( )ｔ
１
α＋ｊωα
＞０
（９）ｅ－α ｔ ２α
α２＋ω２
α＞０
（１０）ｅ－αｔε( )ｔ－ｅαｔε( )－ｔ
－ｊ２ω
α２＋ω２
α＞０
（１１）ｃｏｓω０ｔπδω－ω( )
０ ＋δω＋ω( )[ ]
０
　 －
!
＜ｔ＜
!
（１２）ｓｉｎω０ｔ
π
ｊδω－ω( )
０ －δω＋ω( )[ ]
０
　 －
!
＜ｔ＜
!
三、Ｆ变换的性质
１．线性 齐次性，( )可加性
２．时移
ｆｔ±ｔ( )０Ｆｊ( )ωｅ±ｊωｔ０
３．频移
ｆ( )ｔｅ±ｊω０ｔＦｊωω( )[ ]
０
调制定理
若ｆ( )ｔＦｊ( )ω
则：ｆ( )ｔｃｏｓω０ｔ
１
２ Ｆｊω－ω( )[ ]
０
＋Ｆｊω＋ω( )[ ]{ }
０
ｆ( )ｔｓｉｎω０ｔ
１
２ｊＦｊω－ω( )[ ]
０
－Ｆｊω＋ω( )[ ]{ }
０
【例】　已知：ｆ１( )ｔＦ１ ｊ( )ω
ｆ２( )ｔ＝
ｃｏｓω０ｔ　ｔ２#ｔ#ｔ３（ｔ３ ＝ｔ１＋ｔ２）
０　ｔ＜ｔ２，ｔ＞ｔ
{
３
求：Ｆ２ ｊ( )ω
４．尺度变换：
ｆ（ａｔ） １
ａＦｊ
ω( )ａ
５．对称性：
—２２—
若ｆ( )ｔＦｊ( )ω，则：Ｆ( )ｊｔ２πｆ－ｊ( )ω
６．时域卷积：
ｆ１( )ｔｆ２( )ｔＦ１ ｊ( )ω·Ｆ２ ｊ( )ω
７．频域卷积：（时域相乘）
ｆ１( )ｔ·ｆ２( )ｔ
１
２π
Ｆ１ ｊ( )ωＦ２ ｊ( )ω
８．时域微分：
ｄｆ( )ｔ
ｄｔｊωＦｊ
( )ω
ｆｎ( )ｔ ｊ( )ω ｎＦｊ( )ω
９．时域积分：
∫
ｔ
－
!
ｆ( )ｘｄ( )ｘπＦ( )０δ( )ω ＋
Ｆｊ( )ω
ｊω
若Ｆ( )０ ＝０
则∫
ｔ
－
!
ｆ( )ｘｄ( )ｘ
Ｆｊ( )ω
ｊω
１０．频域微分：
－ｊｔｆ( )ｔ
ｄ
ｄω
Ｆｊ( )ω
( )－ｊｔｎｆ( )ｔ
ｄｎ
ｄωｎ
Ｆｊ( )ω
常用：ｔｆ( )ｔｊ
ｄＦｊ( )ω
ｄω
１１．频域积分：
πｆ( )０δ( )ｔ＋
ｆ( )ｔ
－ｊｔ∫
ω
－
!
Ｆｊ( )ηｄη
１２．帕斯瓦尔等式
信号能量Ｅ＝∫
!
－
!
ｆ２( )ｔｄｔ
＝ １２π∫
!
－
!
Ｆｊ( )ω
２
ｄω
＝∫
!
－
!
Ｅ( )ωｄω
（１）能量谱Ｅ( )ω ＝ Ｆｊ( )ω ２
（２）功率谱
平均功率Ｐ＝ｌｉｍ
Ｔ→!
１
Ｔ∫
Ｔ
２
－Ｔ２
ｆ２( )ｔｄｔ
—３２—
吴大正《信号与线性系统分析》考点精讲
＝ １２π∫
!
－
!
ｌｉｍ
Ｔ→!
Ｆｊ( )ω ２
Ｔ ｄω
＝ １２π∫
!
－
!
Ｐ( )ωｄω
功率谱Ｐ( )ω ＝ｌｉｍ
Ｔ→!
Ｆｊ( )ω ２
Ｔ
【例１】　ｆ( )ｔ＝Ｕｍｃｏｓω０ｔ
Ｐ( )ω ＝
Ｕ２ｍπ
２ δω－ω( )
０ ＋δω＋ω( )[ ]
０
【例２】　 ２００９[ ]北京邮电大学 三画图题２( )小题
已知信号ｘ( )ｔ＝４ｃｏｓ１０πｔ＋π( )４ －６ｃｏｓ２０πｔ＋π( )６ ＋２ｓｉｎ４０πｔ＋π( )３
（１）画出双边幅度谱和相位谱。
（２）计算并画出信号的功率谱。
解　ｘ( )ｔ＝４ｃｏｓ１０πｔ＋π( )４ ＋６ｃｏｓ２０πｔ－５π( )６ ＋２ｃｏｓ４０πｔ－π( )６
（１）幅度谱
相位谱
（２）Ｕｍｃｏｓω０ｔＰ( )ω ＝
Ｕ２ｍπ
２ δω－ω( )
０ ＋δω＋ω( )[ ]
０
Ｐ( )ω ＝
π
２｛４
２ δω－１０( )π ＋δω＋１０( )[ ]π ＋６２ δω－２０( )π ＋δω＋２０( )[ ]π
＋２２ δω－４０( )π ＋δω＋４０( )[ ]π ｝
—４２—
＝２π４δω－１０( )π＋δω＋１０( )[ ]π ＋９δω－２０( )π＋δω＋２０( )[ ]π ＋ δω－４０( )π＋δω＋４０( )[ ]{ }π
１３．周期信号的Ｆｊ( )ω
（１）Ｆｊ( )ω ＝２π∑
!
－
!
Ｆｎδω－ｎ( )Ω
其中：Ｆｎ ＝
１
Ｔ∫
Ｔ
２
－Ｔ２
ｆ( )ｔｅ－ｊｎΩｔｄｔ
（２）Ｆｊ( )ω ＝Ω∑
!
－
!
Ｆ１ ｊｎ( )Ω δω－ｎ( )Ω
其中：Ｆ１ ｊｎ( )Ω ＝Ｆ１ ｊ( )ω ω＝ｎΩ
四、频域分析
１．系统函数Ｈ（ｊω）
Ｈｊ( )ω ＝
ｙｚｓ ｊ( )ω
Ｆｊ( )ω
＝Ｆｈ( )[ ]ｔ
（１）已知系统方程
ｔ０，ｙ″( )ｔ＋５ｙ′( )ｔ＋６ｙ( )ｔ＝３ｆ′( )ｔ＋ｆ( )ｔ
（２）已知系统结构
（３）已知系统模拟框图
２．系统零状态响应
—５２—
吴大正《信号与线性系统分析》考点精讲
ｙｚｓ ｊ( )ω ＝Ｆｊ( )ωＨｊ( )ω
ｙｚｓ( )ｔ＝Ｆ－１ ｙｚｓ ｊ( )[ ]ω
３．系统无失真传输
　ｆ（ｔ）
→
　
→　０　 ｙｚｓ（ｔ）
（１）无失真：
ｙｚｓ( )ｔ＝ｋｆ( )ｔ－ｔｄ
（２）无失真传输条件
①时域ｈ( )ｔ＝ｋδ( )ｔ－ｔｄ
②频域Ｈｊ( )ω ＝ｋｅ－ｊωｔｄ
【例１】　图示系统，已知周期信号ｆ( )ｔ如图所示，ｈ( )ｔ＝
ｓｉｎ５πｔ
πｔ
求ｙｚｓ( )ｔ
【例２】　图示系统
　ｆ（ｔ）
→
　
　Ｈ１（ｊω） →　 　ｈ２（ｔ） →　 ｙｚｓ（ｔ）
ｆ( )ｔ＝∑
!
ｎ＝－
!
３
π
ｅｊｎ ｔ＋π( )２
Ｈ１ ｊ( )ω ＝
１－ ω
３　 ω ＜３
０　 ω ＞
{
３
ｈ２( )ｔ＝
ｓｉｎ３ｔ２
ｔ 求：ｙｚｓ( )ｔ．
【例３】　某系统的输入ｆ( )ｔ与输出ｙｚｓ( )ｔ的关系为：
ｙｚｓ( )ｔ＝
１
π∫
!
－
!
ｆ( )τ
ｔ－τ
ｄτ
—６２—
（１）求系统的频率响应Ｈｊ( )ω．
（２）证明ｙｚｓ( )ｔ与ｆ( )ｔ的能量相等．
【例４】　已知Ｈｊ( )ω ＝Ｈ( )ωｅｊφ
( )ω，激励ｆ( )ｔ＝１＋∑
!
ｎ＝１
１
ｎｃｏｓｎｔ，求：响应ｙ
( )ｔ．
【例 ５】　 若 ｆ( )ｔ是因果函数，并已知 ｆ( )ｔＦｊ( )ω ＝Ｒ( )ω ＋ｊｘ( )ω，试证明：∫
!
０
ｆ２( )ｔｄ( )ｔ＝
２
π∫
!
０
Ｒ２( )ωｄ( )ω．
【例６】　ＬＴＩ系统Ｈｊ( )ω ＝
ｊω
６－ω２＋ｊ５ω
，已知输入ｆ( )ｔ＝ｅ－ｔε( )ｔ，全响应ｙ( )ｔ及一阶导数在“０＋”
的值为：ｙ０( )＋ ＝２ｙ′０( )＋ ＝１，求ｙｚｉ( )ｔ，ｙｚｓ( )ｔ及ｙ( )ｔ．
【例７】　图示为取样示波器中取样电路原理图．
已知输入周期信号ｆ( )ｔ的频谱函数Ｆｊ( )ω ＝∑
４
ｍ＝－４
δω－ｍ( )Ω ，式中Ω＝
２π
Ｔ为基波角频率，Ｔ为周
期 Ｓ( )ｔ＝ ∑
!
ｎ＝－
!
δｔ－ｎＴ( )
ｓ， 式 中 取 样 周 期 Ｔｓ ＝
１０
９Ｔ，Ｈｊ
( )ω
２Ｔｓ　 ω ＜０．４５Ω
０　 ω ＞０．４５
{ Ω
， 求 输 出
ｙ( )ｔ．用ｆ( )ｔ[ ]的有关函数表示即可
【例８】　图示系统
ｆ( )ｔ＝∑
!
ｎ＝－
!
ｅｊｎΩｔ，Ω ＝１ｒａｄ／ｓ，ｓ( )ｔ＝ｃｏｓｔ，ｈ１( )ｔ＝ｅ－ ｔ，Ｈ２ ｊ( )ω
１　 ω ＜１．５ｒａｄ／ｓ
０　 ω ＞１．５
{ ｒａｄ／ｓ
，求ｙ( )ｔ．
【例９】　图示系统
—７２—
吴大正《信号与线性系统分析》考点精讲
ｈ１( )ｔ＝
ｄ
ｄｔ
ｓｉｎ２ｔ
２π( )ｔ，Ｈ２ ｊ( )ω ＝ｅ－ｊπω，ｈ３( )ｔ＝
ｓｉｎ６ｔ
πｔ
，ｈ４( )ｔ＝ε( )ｔ，ｆ( )ｔ＝ｓｉｎ４ｔ＋ｃｏｓｔ，求：ｙ( )ｔ．
五、取样定理
（１）冲击取样
Ｓ( )ｔ＝δＴ( )ｔ＝∑
!
ｎ＝－
!
δｔ－ｎＴ( )
ｓ
（２）脉冲取样
Ｓ( )ｔ＝ＰＴ( )ｔ＝∑
!
ｎ＝－
!
ｇτ ｔ－ｎＴ( )
ｓ
Ｔｓ为取样周期，ｆｓ＝
１
Ｔｓ
为取样频率
【例】　ｆ( )ｔ的频谱，Ｆｊ( )ω
１　 ω ＜２ｒａｄ／ｓ
０　 ω ＞２
{ ｒａｄ／ｓ
，对ｆ( )ｔｃｏｓ２ｔ均匀抽样的最大Ｔｓ为（　　）
Ａ．π２　　　　　　　Ｂ．
π
４　　　　　　　Ｃ．π　　　　　　　Ｄ．２π
【例】　有限频带信号的最高频率为２００Ｈｚ，若对下列信号进行时域抽样，求最小抽样频率ｆｓ．
（１）ｆ３( )ｔ
（２）ｆ２( )ｔ
（３）ｆ( )ｔｆ３( )ｔ
（４）
ｄｆ( )ｔ
ｄｔ
—８２—
第五章 　 复频域分析
本章重点框架图
一、双边Ｌ变换
二、单边Ｌ变换
三、常用信号的Ｆ（ｓ）
四、单边Ｌ的性质
五、Ｌ逆变换
六、系统的复频域分析
七、Ｆ（ｊω）与Ｆ（ｓ）的关系
一、双边Ｌ变换
１．定义：
ｆ( )ｔ＝
１
２πｊ∫
σ＋ｊ!
σ－ｊ!
Ｆ( )ｓｅｓｔｄｓ
Ｆ( )ｓ＝∫
!
－
!
ｆ( )ｔｅ－ｓｔｄｔ
ｓ＝σ＋ｊω( )复频率
２．存在条件( )充分条件
∫
!
－
!
ｆ( )ｔｅ－ｓｔｄｔ＜!
即：∫
!
－
!
ｆ( )ｔｅ－σｔｄｔ＜!
３．收敛域
（１）部分Ｓ平面收敛
①因果信号Ｒｅ( )ｓ＞σ０
②反因果信号Ｒｅ( )ｓ＜σ０
③双边信号σ０１ ＜Ｒｅ( )ｓ＜σ０２
（２）整个Ｓ平面均收敛
ｆ( )ｔ为有始有终的有界信号
—９２—
吴大正《信号与线性系统分析》考点精讲
（３）Ｓ平面均不收敛
二、单边Ｌ变换
１．定义：
ｆ( )ｔ＝
１
２πｊ∫
σ＋ｊ!
σ－ｊ!
Ｆ( )ｓｅｓｔｄｓ　ｔ０
０　ｔ＜
{
０
Ｆ( )ｓ＝∫
!
０－
ｆ( )ｔｅ－ｓｔｄｔ
２．收敛域
（１）部分Ｓ平面收敛Ｒｅ( )ｓ＞σ０
（２）Ｓ平面均收敛
（３）Ｓ平面均不收敛
对于单边Ｌ变换
ｆ( )ｔＦ( )ｓ一一对应
三、常用信号的Ｆ（ｓ）
１．δ( )ｔ１
２．ε( )ｔ
１
ｓ
３．δ′( )ｔＳ　δ( )ｎ ( )ｔＳｎ
４．ｅｓ０ｔε( )ｔ　
１
ｓ－ｓ０
　ｅαｔε( )ｔ　
１
ｓ－α
ｅ－αｔε( )ｔ
１
ｓ＋α
　ｅｊβｔε( )ｔ
１
ｓ－ｊβ
ｅ－ｊβｔε( )ｔ
１
ｓ＋ｊβ
５．ｓｉｎβｔε( )ｔ β
ｓ２＋β２
６．ｃｏｓβｔε( )ｔ
ｓ
ｓ２＋β２
７．ｓｈβｔε( )ｔ β
ｓ２－β２
８．ｃｈβｔε( )ｔ
ｓ
ｓ２－β２
９．ｔｎε( )ｔ
ｎ！
ｓｎ＋１
四、单边Ｌ的性质
１．线性 齐次性，( )可加性
—０３—
２．尺度变换
若ｆ( )ｔＦ( )ｓ，则，ｆ( )ａｔ
１
ａＦ
ｓ( )ａ　ａ＞０ａ( )为实常数
３．时移
若ｆ( )ｔＦ( )ｓ，则ｆｔ－ｔ( )
０ εｔ－ｔ( )
０ Ｆ( )ｓｅ－ｓｔ０　ｔ００
【例１】
【例２】
“周期信号”的Ｆ( )ｓ
若ｆ( )ｔＦ( )ｓ，则ｆＴ( )ｔ
Ｆ( )ｓ
１－ｅ－ｓＴ
４．复频移
若：ｆ( )ｔＦ( )ｓ，则ｅｓ０ｔｆ( )ｔＦｓ－ｓ( )
０ 　ｓ０为复常数
５．时域微分
若ｆ( )ｔＦ( )ｓ，则
ｄｆ( )ｔ
ｄｔＳＦ
( )ｓ－ｆ０( )
－
推广：ｆ″( )ｔｓ２Ｆ( )ｓ－ｓｆ０( )
－ －ｆ′０( )
－
ｆ( )ｎ ( )ｔｓｎＦ( )ｓ－ｓｎ－１ｆ０( )
－ －ｓ
ｎ－２ｆ′０( )
－ －… －ｆ
ｎ－( )１ ０( )
－
—１３—
吴大正《信号与线性系统分析》考点精讲
６．时域积分
若：ｆ( )ｔＦ( )ｓ，则∫
ｔ
０
ｆ( )ｘｄｘ
Ｆ( )ｓ
ｓ
（１）积分下限若为 －
!
∫
ｔ
－
!
ｆ( )ｘｄｘ
∫
０－
－
!
ｆ( )ｘｄｘ
ｓ ＋
Ｆ( )ｓ
ｓ
（２）推广
∫
ｔ
０
( )
－
ｎ
ｆ( )ｘｄｘ
Ｆ( )ｓ
ｓｎ
【例１】
【例２】
７．时域卷积
ｆ１( )ｔｆ２( )ｔＦ１( )ｓ·Ｆ２( )ｓ
８．Ｓ域卷积( )时域相乘
ｆ１( )ｔ·ｆ２( )ｔ
１
２πｊ
Ｆ１( )ｓＦ２( )ｓ
９．Ｓ域微分
若：ｆ( )ｔＦ( )ｓ，则 －？( )ｔｎｆ( )ｔ
ｄｎＦ( )ｓ
ｄｓｎ
当ｎ＝１时，ｔｆ( )ｔ －
ｄＦ( )ｓ
ｄｓ
１０．Ｓ域积分
若：ｆ( )ｔＦ( )ｓ且ｌｉｍ
ｔ→０
ｆ( )ｔ
ｔ存在，则
ｆ( )ｔ
ｔ∫
!
ｓ
Ｆ( )ηｄη
—２３—
１１．初值定理
若：ｆ( )ｔＦ( )ｓ且ｌｉｍ
ｓ→!
ＳＦ( )Ｓ存在，则ｆ０( )
＋ ＝ｌｉｍｓ→!
ＳＦ( )Ｓ
１２．终值定理
若：ｆ( )ｔＦ( )ｓ且ｆ( )
!
存在，则ｆ( )
!
＝ｌｉｍ
ｓ→０
ＳＦ( )Ｓ
五、Ｌ逆变换
ｆ( )ｔ＝
１
２πｊ∫
σ＋ｊ!
σ－ｊ!
Ｆ( )ｓｅｓｔｄｓ　ｔ０
０　ｔ＜
{
０
（１）部分分式展开
（２）留数法
（１）部分分式展开
Ｆ( )ｓ＝
Ｂ( )ｓ
Ａ( )ｓ
＝
ｂｍｓ
ｍ ＋ｂｍ－１ｓ
ｍ－１＋… ＋ｂ１ｓ＋ｂ０
ｓｎ＋ａｎ－１ｓ
ｎ－１＋ａ１ｓ＋ａ０
　ｍ＜ｎ
①Ｆ( )ｓ有单阶极点
Ｆ( )ｓ＝∑
ｎ
ｉ＝１
ｋｉ
ｓ－ｓｉ
ｋｉ＝ ｓ－ｓ( )
ｉＦ( )ｓ ｓ＝ｓｉ
＝Ｂ
( )ｓ
Ａ′( )ｓ ｓ＝ｓｉ
ｆ( )ｔ＝∑
ｎ
ｉ＝１
ｋｉｅ
ｓｉｔ
②Ｆ( )ｓ有高阶极点
设Ｆ( )ｓ在ｓ＝ｐ１处有ｒ阶极点
Ｆ( )ｓ＝
Ｂ( )ｓ
Ａ( )ｓ
＝
Ｂ( )ｓ
ｓ－ｐ( )
１
ｒ＝
ｋ１
ｓ－ｐ( )
１
ｒ＋
ｋ２
ｓ－ｐ( )
１
ｒ－１＋… ＋
ｋｉ
ｓ－ｐ( )
１
ｒ－ｉ＋１＋… ＋
ｋｒ
ｓ－ｐ１
其中：ｋｉ＝
１
ｉ－( )１！
ｄｉ－１
ｄｓｉ－１ ｓ－ｐ( )
１
ｒ×Ｆ( )[ ]ｓ
ｓ＝ｐ１
１
ｓ－ｐ( )
１
ｉ
１
ｉ－( )１！
ｔｉ－１ｅｐ１ｔε( )ｔ
（２）留数法
当 ｓ＝ｐ→ !
时，Ｆ( )ｓ →０
ｆ( )ｔ＝
１
２πｊ∫
σ＋ｊ!
σ－ｊ!
Ｆ( )ｓｅｓｔｄｓ＝
０　ｔ＜０
∑ＲｅｓＦ( )ｓｅｓｔ，Ｐ[ ]ｉ　ｔ
{ ０
①若Ｆ( )ｓ在ｓ＝ｐ１有单阶极点
—３３—
吴大正《信号与线性系统分析》考点精讲
【例】
２．梅森公式
Ｈ( )· ＝∑ＰｉΔｉ
Δ
Δ：流图行列式
１－∑Ｌｉ＋∑ＬｉＬｊ－∑ＬｉＬｊＬｋ＋…
Ｐｉ：第ｉ条前向通路增益
Δｉ：第ｉ条前向通路的余因子
【例】　图示系统
求：＜１＞Ｈ（ｚ）
（２）为使系统稳定，确定Ｋ的取值范围
（３）当ｋ＝０时，输入ｆ（ｋ）＝１＋５ｃｏｓ（πｋ／２）
求：稳态响应ｙｓ（ｋ）
四、系统模拟
１．直接模拟
２．级联模拟
３．并联模拟
【例１】　（１）Ｈ（ｓ）的零极图如下．且Ｈ（∞）＝１，求阶跃响应ｇ（ｔ）．
—０５—
（２）Ｈ（ｚ）的零极图如下．且已知Ｈ（０）＝１，求ｈ（ｋ）．
【例２】　系统如图，为使系统稳定，ｋ１，ｋ２，如何取值．
【例３】　图示系统，ｆ( )ｋ＝５＋５ｃｏｓπ２ｋ，求稳态响应．
【例４】　离散因果系统为：ｙ（ｋ）＋０．２ｙ（ｋ－１）－０．２４ｙ（ｋ－２）＝ｆ（ｋ）＋ｆ（ｋ－１）
（１）求ｈ（ｋ）
（２）判断系统的稳定性
（３）ｆ（ｋ）＝１２ｃｏｓ２πｋ，求稳态响应
【例５】　ＬＴＩ系统
当ｆ( )ｋ＝
１　０＜ｔ＜２( )ｓ
－１　２＜ｔ＜４０( )ｓ
０　
{
其余
ｙｚｓ（ｔ）为试用最小的功能部件
（如加法器，数乘器，积分器，延时器）构成系统框图
—１５—
吴大正《信号与线性系统分析》考点精讲
【例６】　已知ｙ（ｋ）＋１．５ｙ（ｋ－１）－ｙ（ｋ－２）＝ｆ（ｋ－１）
（１）系统为因果系统，求ｈ（ｋ）
（２）系统为稳定系统，求ｈ（ｋ），并计算ｆ（ｋ）＝（－０．５）ｋε（ｋ）的零状态响应
—２５—
第八章 　 系统的状态变量分析
本章重点框架图
一、连续系统的状态方程
二、离散系统的状态方程
三、状态方程的解
一、连续系统的状态方程
ｎ个状态变量，ｐ个输入，ｑ个输出
Ｘ
·
＝ＡＸ＋Ｂｆ
Ｙ＝ＣＸ＋Ｄｆ
１． →电路图 状态方程
（１）选独立电容电压，独立电感电流为状态变量
（２）对电容列ＫＡＬ方程，对电感列ＫＶＬ方程
（３）消去非状态变量
（４）整理成标准形式
２． →微分方程 状态方程
３． →信号流图 状态方程
二、离散系统的状态方程
Ｘ（ｋ＋１）＝ＡＸ（ｋ）＋Ｂｆ（ｋ）
Ｙ（ｋ）＝ＣＸ（ｋ）＋Ｄｆ（ｋ）
列方程过程与连续系统相似
—３５—
吴大正《信号与线性系统分析》考点精讲
三、状态方程的解
１．预解矩阵
Φ( )ｓ＝[ ]ＳＩ－Ａ－１
Φ( )ｚ＝[ ]ｚＩ－Ａ－１ｚ
２．状态转移矩阵
ｅＡｔ＝Ｌ－１ Φ( )[ ]ｓ
Ａｋ ＝Ｅ－１ Φ( )[ ]ｚ
四、由状态方程判别系统的稳定性
１．连续系统
ｘ
·
( )ｔ＝Ａｘ( )ｔ＋Ｂｆｙ( )ｔ＝Ｃｘ( )ｔ＋Ｄｆ( )ｔ
Ｓｘ( )ｓ－ｘ０( )
－ ＝Ａｘ( )ｓ＋ＢＦ( )ｓ
[ ]ＳＩ－Ａｘ( )ｓ＝ｘ０( )
－ ＋ＢＦ( )ｓ
ｘ( )ｓ＝[ ]ＳＩ－Ａ－１ｘ０( )
－ ＋[ ]ＳＩ－Ａ－１ＢＦ( )ｓ
ｘｚｓ( )ｓ＝[ ]ＳＩ－Ａ－１ＢＦ( )ｓ
ｙｚｓ( )ｓ＝Ｃｘｚｓ( )ｓ＋ＤＦ( )ｓ＝ Ｃ( )ＳＩ－Ａ－１[ ]Ｂ＋ＤＦ( )ｓ
Ｈ( )ｓ＝Ｃ( )ＳＩ－Ａ－１Ｂ＋Ｄ＝Ｃ·
ａｄｊ( )ＳＩ－Ａ
ｄｅｔ( )ＳＩ－Ｓ
Ｂ＋Ｄ＝
Ｃａｄｊ( )ＳＩ－ＡＢ＋Ｄｄｅｔ( )ＳＩ－Ａ
ｄｅｔ( )ＳＩ－Ａ
Ａ( )ｓ＝ｄｅｔ( )ＳＩ－Ａ ＝０的根全部位于Ｓ的左半开平面→系统稳定
２．离散系统
同理可得：Ａ( )ｚ＝ｄｅｔ( )ｚＩ－Ａ ＝０的全部位于单位圆内→系统稳定
【例１】　列出上述系统的状态方程及输出方程
【例２】　列出图示系统的状态方程及输出方程，并分析该系统是否稳定。
【例３】　连续系统的状态方程及输出方程为：
—４５—
ｘ１
·
ｘ２
·
ｘ３












·
＝
０ －１ ２
１ ０ ０
－５ ０ －







６
ｘ１
ｘ２
ｘ










３
＋








０
０
１
ｆ（ｔ）
ｙ（ｔ）＝[ ]０　０　１
ｘ１
ｘ２
ｘ










３
求描述系统的输入输出微分方程．
【例４】　图示已标出状态变量ｘ１，ｘ２．
（１）写出状态方程．
（２）为使系统稳定，ａ，ｂ应满足什么条件。
【例５】　复合系统由两个子系统组成，分别为ｓａ，ｓｂ
ｓａ：
ｘａ１
·
ｘａ２








·
＝
１ －２[ ]２ １
ｘａ１
ｘａ
[ ]
２
＋[ ]１０ｆ１
ｙ１（ｔ）＝［１　 －１］
ｘａ１
ｘａ
[ ]
２
ｓｂ：
ｘｂ１
·
ｘｂ２








·
＝
２ －１
－[ ]２ １
ｘｂ１
ｘｂ
[ ]
２
＋[ ]２０ｆ２
ｙ２（ｔ）＝［０　 －１］
ｘｂ１
ｘｂ
[ ]
２
（１）写出复合系统的状态方程和输出方程的标准形式
—５５—
吴大正《信号与线性系统分析》考点精讲
（２）画出复合系统的信号流图，并标出ｘａ１，ｘａ２，ｘｂ１，ｘｂ２，求复合系统的Ｈ（ｓ）．
【例６】　图示系统，已知ｘ１（０－）＝２，ｘ２（０－）＝１．
（１）写出系统微分方程，求出初始条件ｙ（０－），ｙ′（０－）
（２）若ｆ（ｔ）＝ｅ－２ｔε（ｔ），求ｙ（ｔ）．
—６５—