概要信息：

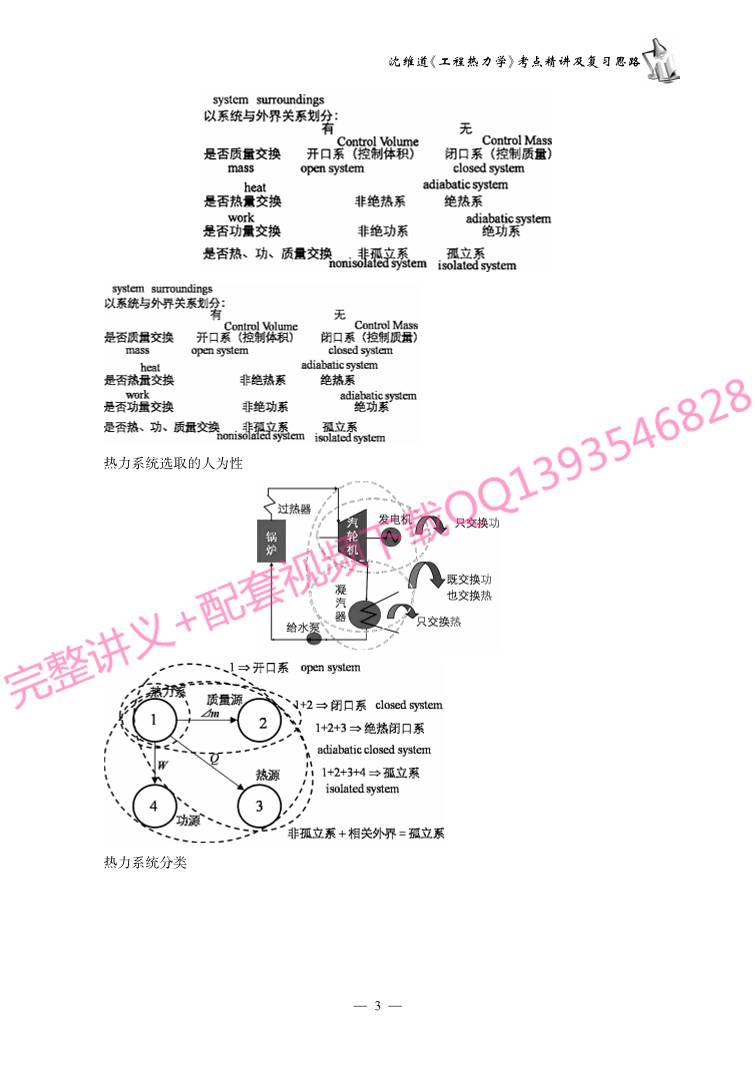
目　　录
第一章　基本概念 （１）
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
第二章　热力学第一定律 （２１）
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
第三章　理想气体 （３９）
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
第四章　理想气体的热力过程 （４９）
!!!!!!!!!!!!!!!!!!!!!!!!!!!
第五章　热力学第二定律 （６９）
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
第六章　热力学一般关系式 （１００）
!!!!!!!!!!!!!!!!!!!!!!!!!!!!
第七章　实际气体和水蒸气的性质 （１１５）
!!!!!!!!!!!!!!!!!!!!!!!!!
第八章　气体与蒸汽的流动 （１４０）
!!!!!!!!!!!!!!!!!!!!!!!!!!!!
第九章　压气机的热力过程 （１６８）
!!!!!!!!!!!!!!!!!!!!!!!!!!!!
第十章　气体动力循环 （１７５）
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
第一章　基本概念
一、基本概念及其相互关系
主要基本概念：
热力系，工质，工质的状态，（非）平衡状态，
状态参数，状态公理，状态方程，（非）准平衡（静态）过程，（不）可逆过程，热力循环。
衍生基本概念：
（非）孤立系，闭口系，开口系，热平衡，力平衡，弛豫时间，基本状态参数（ｐ、ｖ、Ｔ），热力学第零定
律、温标，强度量，广延量，比参数，摩尔参数，状态参数坐标图，功、热，耗散效应，（不）可逆循环，正
（逆）向循环，循环经济性指标。
次衍生基本概念：
简单可压缩热力系 ，（非）均匀状态，（非）稳定状态，热力学温标、摄氏温标、郎肯温标、华氏温
标、经验温标，国际温标，理想气体状态方程，过程量，示功图，示热图，循环热效率，供暖系数，制冷
系数。
—１—
沈维道《工程热力学》考点精讲及复习思路
不仅要关注基本概念本身，更要关心概念之间横向和纵向的关系，对于我们理解概念、从而能够
用自己的语言正确地表述概念非常重要。
概念之间横向和纵向的关系的基础就是科学方法，正确的方法和思维方式是基础。
由基本概念及其相互间关系织成的一张网，才是工程热力学的本质内容，任何孤立地、片面地理
解或死记硬背基本概念的定义、意义的方式都是不可取的。
二、重要的基本概念
考点１：热力学的研究对象———热力系（ｓｙｓｔｅｍ）
把这种按照某种目的人为地从周围环境中分离出来进行研究的对象就叫做热力学系统，简称系
统或热力系。热力系以外的东西称为外界，也称为环境。热力系与外界分开的界面称为边界。
热力系、边界、外界都是人为抽象出来的概念。其边界可以是真实的，也可以是假想的；可以是固
定的，也可以是运动的。完全是人的主观意志的体现。
热力系统分类
—２—
热力系统选取的人为性
热力系统分类
—３—
沈维道《工程热力学》考点精讲及复习思路
一个特殊的热力系———简单可压缩热力系的由来：
理想化方法→使热力系尽量简单，突出热能与机械能的转换→只有两种能量传递方式：热量和体
积功
例１－１填空：热力系统是人为指定的某个具体研究分析对象，根据分析方法的不同有两种不同
的研究系统，一种是 的系统，又称为 ；另一种是 的系统，又称为
。（天津大学考研试题）
例１－２填空：孤立系是指　　　　　　　　　　　　　　，简单热力系统是指　　　　　　　
　　　　　　　。（北京理工大学考研试题）
考点２：热力系的描述———状态与状态参数（ｐｒｏｐｅｒｔｙ）
状态：某一瞬间热力系所呈现的宏观物理状况。
状态参数：描述热力系状态的宏观物理量。
并不是所有的状态都有状态参数。只有当热力系内部参数处处相等时，其内部状态才能用状态
参数来表征。即　　　ｐ１＝ｐ２＝ｐ
压力处处相等，这时热力系处于力平衡。
温度处处相等，这时热力系处于热平衡。
—４—
压差、温差通常称为不平衡势。
化学不平衡势为零时就处于化学平衡，
相不平衡势为零时就处于相平衡。
温差 — 热不平衡势
压差 — 力不平衡势
化学反应 — 化学不平衡势
相变—相不平衡势
如果一个热力系所有的不平衡势都为零，那么
就可以用所有的状态参数去描述它了。我们称这时的热力系处于平衡状态，简称平衡态（ｅｑｕｉｌｉｂ
ｒｉｕｍｓｔａｔｅ）。
原始定义是：在不受外界影响的条件下（重力场除外），如果热力系的状态参数长时间不随时间变
化，则该热力系所处的状态就称为平衡状态。
平衡的本质：不存在不平衡势，可以用状态参数去描述。
注意平衡状态与稳定状态的区别。
稳定：参数不随时间变化。
如果稳定但存在不平衡势差，去掉外界影响，则状态变化。
结论：稳定不一定平衡，但平衡一定稳定。
注意平衡状态与均匀状态（ｕｎｉｆｏｒｍｓｔａｔｅ）的区别。
均匀：空间上
稳定：时间上。
例如处于相平衡的水和水蒸气 。
结论：平衡不一定均匀，均匀则一定是平衡的。
状态参数只能描述平衡态，非平衡态不能用状态参数来描述，因而也就无法进行研究，因此工程
热力学只能研究平衡态，严格说是平衡态热力学。
可见，并不是所有的状态都有状态参数。状态参数存在的条件是———平衡状态。
非平衡态则不能用状态参数表征，或者说非平衡态没有状态参数。
状态参数：描述热力系平衡状态的物理量。
工程热力学只能研究平衡态，严格说是平衡态热力学。
例１－３是非题：只有处于平衡状态的系统才能用状态参数来描述。（　　）（南航考研试题）
例１－４简答题：平衡状态和均匀状态有何异同？（西北工业大学考研试题）
—５—
沈维道《工程热力学》考点精讲及复习思路
例１－５简答题：简述热力系平衡状态和稳定状态的区别。（北航考研试题）
热力系与工质的关系：
热力系不可能是虚无的，它通常是由某些工作物质（简称工质）所组成的。通常把热力系与工质
不加区分，热力系的状态参数也就通常与物质的状态联系在一起，成为描述物质宏观状况的状态参
数。如压力、温度、体积等。
简单可压缩系的基本状态参数
压力ｐ、温度Ｔ、比体积ｖ（可测量）
①比体积（质量体积，比容）ｖ
ｖ＝Ｖｍ ＝
１
ρ ｍ３／[ ]ｋｇ
反映工质聚集的疏密程度的状态参数。
基本状态参数
①比体积（质量体积，比容）ｖ
②压力 （压强，ｐｒｅｓｓｕｒｅ）ｐ
流体单位面积上所作用的力的法向分量称为压力或压强。
ｐ＝
Ｆｎ
Ａ Ｎ／ｍ
[ ]２ ，[ ]Ｐａ
其他常用单位：
　　　 １ｂａｒ＝１０５　Ｐａ，　　１ＭＰａ＝１０６Ｐａ
　　　 １ａｔｍ ＝７６０ｍｍＨｇ＝１．０１３
!
１０５Ｐａ
　　　 １ｍｍＨｇ＝１３３．３Ｐａ
　　　 １ａｔ＝７３５．６ｍｍＨｇ＝９．８０６６５
!
１０４Ｐａ
微观意义：大量分子撞击器壁的平均结果。
压力ｐ的测量
一般是绝对压力与环境压力的相对值　 ———相对压力
注意：只有绝对压力ｐ才是状态参数
当ｐ ＞ｐｂ→表压力ｐｇ→ｐ＝ｐｇ＋ｐｂ
当ｐ ＜ｐｂ→真空度ｐｖ→ｐ＝ｐｂ－ｐｖ
—６—
其它压力测量方法
高精度测量：活塞式压力计
工业或一般科研测量：压力传感器
　　　
③温度 （ｔｅｍｐｅｒａｔｕｒｅ）Ｔ
温度完全是一个人为设计的概念。其概念是建立在热力学第零基础之上的宏观概念 。
在没有外界影响的条件下，只要经过足够长的时间，它们将达到相同的冷热程度，传热就会停止。
该两物体的物理状况不再发生变化，根据平衡的定义，就把这种状况称为热平衡。
热力学第零定律ｔｈｅｚｅｒｏｔｈｌａｗｏｆｔｈｅｒｍｏｄｙｎａｍｉｃｓ
美国，Ｒ．ＷＦｏｗｌｅｒ），１９３１年
如果两个系统分别与第三个系统处于热平衡，则两个系统彼此必然处于热平衡。
温度测量的理论基础　　　　 Ｂ　温度计
温度的热力学定义
处于同一热平衡状态的各个热力系，必定有某一宏观特征彼此相同，用于描述此宏观特征的物理
量
"
温度。
温度是确定一个系统是否与其它系统处于热平衡的物理量。
与压力、比体积不同的是，温度的定义并不能直接确定其数值，反映了温度概念的抽象性，不
直观。
温度的数值表示法称作温标。
温度计原理：物质 （水银，铂电阻，热电偶）、特性 （体积膨胀，阻值，电势）
—７—
沈维道《工程热力学》考点精讲及复习思路
显然，温度计刻度显示的并不是温度本身！
如图所示的两个温度计除了０℃和１００℃ 外的其他读数一样吗？
这种依赖于测温物质的某一物理性质建立的温标称为经验温标。经验温标不是一种客观的
温标。
因此，必须选择一个不依赖于物性而独立存在的温标！
　　
最客观的温标———热力学绝对温标
热力学摄氏温标定义为：ｔ（℃）＝Ｔ（Ｋ）－２７３．１５
摄氏温度与华氏温度换算ｔ（℃）＝　　［ｔ（
"
）－３２］
朗肯温度与华氏温度换算ｔ（
"
）＝Ｔ（Ｒ）－４５９．６７
对温标的建立做出贡献的ＶＩＰ们
热力学温标—创始人—ＷｉｌｉａｍＴｈｏｍｓｏｎ—（１８２４－１９０７）
—８—
摄氏温度—创始人—ＡｎｄｅｒｓＣｅｌｓｉｕｓ— （１７０１－１７４４）
朗肯温度—创始人—ＷｉｌｉａｍＪｏｈｎ— ＭａｃｑｕｏｒｎＲａｎｋｉｎｅ—（１８２０－１８７２）
华氏温度—创始人—ＤａｎｉｅｌＧａｂｒｉｅｌＦａｈｒｅｎｈｅｉｔ（１６８６－１７３６）
状态参数的特性
物理特性：
①与平衡态一一对应。
②状态确定，则状态参数也确定，反之亦然
③状态参数变化量与过程无关
数学特性：
①点函数，态函数
②单值函数
③全微分，积分与路径无关
状态参数的数学特征
ｚ＝ｚ（ｘ，ｙ）ｄｚ是全微分
∫
２
１，ａ
ｄｚ＝∫
２
１，ｂ
ｄｚ＝∫
２
１
ｄｚ＝ｚ２－ｚ１
∮ｄｚ＝０
ｄｚ＝ ｚ
( )ｘｙ
ｄｘ＋ ｚ
( )ｙｘ
ｄｙ
充要条件：
２ｚ
ｘｙ
＝ 
２ｚ
ｙｘ
可判断是否是状态参数
强度参数与广延参数
ｉｎｔｅｎｓｉｖｅｐｒｏｐｅｒｔｙ：
·强度参数
—９—
沈维道 工程热力学》考点精讲及复习思路
·与物质的量无关的参数
·如压力ｐ、温度Ｔ
·不具有加和性
ｅｘｔｅｎｓｉｖｅｐｒｏｐｅｒｔｙ
·广延参数
·与物质的量有关的参数
"
·如质量ｍ、容积Ｖ、内能Ｕ、焓Ｈ、熵Ｓ
·Ｘ具有加和性Ｘ＝∑
Ｌ
ｉ＝１
Ｘｉ
右边两个热力系是否处于相同的状态？
强度参数比广延参数更真实地反映了热力系的本质。
ｅｘｔｅｎｓｉｖｅｐｒｏｐｅｒｔｙ→ｉｎｔｅｎｓｉｖｅｐｒｏｐｅｒｔｙ
把广延参数→强度参数
比参数：　　　　ｖ＝Ｖｍ　ｕ＝
Ｕ
ｍ　ｈ＝
Ｈ
ｍ　ｓ＝
Ｓ
ｍ
ｓｐｅｃｉｆｉｃｐｒｏｐｅｒｔｙ　比体积　 比内能　 比焓　 比熵
摩尔参数：　　　Ｖｍ ＝
Ｖ
ｎ　Ｕｍ ＝
Ｕ
ｎ　Ｈｍ ＝
Ｈ
ｎ　Ｓｍ ＝
Ｓ
ｎ
ｍｏｌａｒｐｒｏｐｅｒｔｙ摩尔体积　 摩尔内能　　摩尔焓　摩尔熵
单位：／ｋｇ，／ｋｍｏｌ　　它们具有强度量的性质
例１－６简答题：压力和温度有何共性和异性？温度有“温标”，压力有“压标”吗？（西北工业大学
考研试题）
答：压力和温度的共性是：都是状态参数，且都是强度参数。从微观上看，压力和温度都是分子无
规则热运动的结果，但它们的本质是不同的：压力有方向，说明它反映的是热力系的有序性，而温度没
有，反映的是无序性。压力是功的驱动力，而温度是热的驱动力。温度的数值靠“温标”确定，而压力
则不需要，因为压力所采用的Ｎ／ｍ２的单位是确定的，是个导出单位。
考点３：状态参数间的关系———状态方程
平衡状态可用一组状态参数描述，但不是所有的状态参数确定了平衡状态才确定。而是取决于
热力系独立状态参数个数，即热力系的自由度。
独立状态参数个数是多少呢？
状态公理（ｓｔａｔｅｐｏｓｔｕｌａｔｅ）
对于组元一定的闭口系统，当其处于平衡状态时，可以用与该系统有关的功形式的数目ｊ加一个
描述传热方式的独立状态参数，即共（ｊ十１）个独立状态参数来确定。
独立参数数目ｉ＝不平衡势差数
—０１—
＝能量转换式的数目
＝各种功的方式＋热量＝ｊ＋１
简单可压缩系统：ｉ＝１＋１＝２
绝热简单可压缩系统
#
ｉ＝？
这是基本状态参数（ｐ，ｖ，Ｔ）之间的关系以及ｕ，ｈ，ｓ表达式存在的基础。
状态方程
"
基本状态参数（ｐ，ｖ，Ｔ）之间的关系
ｕ，ｈ，ｓ，ｃｐ，ｃｖ表达式"
ｕ，ｈ，ｓ，ｃｐ，ｃｖ与基本状态参数
（ｐ，ｖ，Ｔ）之间的关系
状态方程　ｅｑｕａｔｉｏｎｏｆｓｔａｔｅ
状态方程的形式
隐函数形式 ｆ（ｐ，ｖ，Ｔ）＝０
显函数形式 ｖ＝ｆ（ｐ，Ｔ）Ｔ＝ｆ（ｐ，ｖ）
Ｐ＝ｆ（ｖ，Ｔ）
状态方程的具体形式取决于工质的性质
理想气体的状态方程ｐｖ＝ＲｇＴ　ｐＶ＝ｍＲｇＴ
实际工质的状态方程
例１－７是非题：状态方程是描述ｐ、Ｖ、Ｔ三个基本状态参数之间关系的方程。（　　）（北京科技
大学考研试题）
坐标图
简单可压缩热力系 ｉ＝２，可以在平面坐标图上显示状态。
说明：
１）系统任何平衡态可表示在坐标图上。
２）过程线中任意一点为平衡态。
３）非平衡态无法在图上用实线表示。
考点４：状态参数的变化———热力过程（ｐｒｏｃｅｓｓ）
热力过程是热力系内部与外界联系的一座桥梁，只有通过热力过程才能实现热能与机械能之间
的转换，达到热力学的研究目的。
但是，热力过程的描述出现困难。其状态是非平衡态，无法用状态参数描述。
解决问题的方法是把热力过程理想化———提出“准静态过程”和“可逆过程”的概念。
准静态（准平衡）过程ｑｕａｓｉ－ｓｔａｔｉｃ（ｑｕａｓｉ－ｅｑｕｉｌｉｂｒｉｕｍ）ｐｒｏｃｅｓｓ
—１１—
沈维道《工程热力学》考点精讲及复习思路
一般过程ｐ１＝ｐ０＋重物
突然去掉重物
最终：ｐ２＝ｐ０、Ｔ２＝Ｔ０
ｐ１＝ｐ０＋重物、Ｔ１＝Ｔ０
　　　
假如重物有无限多层
每次只去掉无限薄一层
系统随时接近于平衡态
准静态过程定义：把这种由一系列无限接近平衡状态的状态所组成的热力过程称为准静态过程
（ｑｕａｓｉ－ｓｔａｔｉｃｐｒｏｃｅｓｓ）或准平衡过程（ｑｕａｓｉ－ｅｑｕｉｌｉｂｒｉｕｍ　ｐｒｏｃｅｓｓ）。
无限接近→无限缓慢
准静态过程的工程条件
破坏平衡所需时间（外部作用时间）＞＞恢复平衡所需时间（驰豫时间）
有足够时间恢复新平衡
#
准静态过程
无限缓慢→足够缓慢
无限接近→有限近似
准静态过程的意义
既是平衡，又是变化。
既可以用状态参数描述，又可进行热功转换。
准静态过程是矛盾的统一体。
工程上大多数热力过程都可以看作是准静态过程 。
但仅有准静态过程是不够的，热力学还需要比准静态过程更严格的条件。这就是可逆过程。
可逆过程的定义ｒｅｖｅｒｓｉｂｌｅｐｒｏｃｅｓｓ
热力系经历一个热力过程后，如令过程沿原路径逆行而能使热力系与外界同时恢复到原态，不留
下任何痕迹，则此过程称为可逆过程 。
—２１—
反之，如果当热力系沿原路径逆行恢复到原态而外界没有恢复到原态，或外界恢复到原态而热力
系没有恢复到原态，即热力系和外界没有同时恢复到原态，则原来的热力过程就是一个不可逆过程。
不可逆根源：不平衡势差、耗散效应
举例：非准静态过程ｎｏｎ－ｑｕａｓｉ－ｓｔａｔｉｃｐｒｏｃｅｓｓ
工质做功
$
Ｗ　＝ｐＡｄｘ＝ｐｄＶ　　 Ｗ ＝∫
２
１
ｐｄＶ
外界得功δＷ ＝ｐＳＵＲＲＡｄｘ＝ｐＳＵＲＲｄＶ　Ｗ ＝∫
２
１
ｐＳＵＲＲｄＶ
显然，只有当时ｐ＝ｐＳＵＲＲ，过程可逆向进行，满足热力系与外界同时返回原态的可逆条件。
结论：如果是非准静态过程，则一定是不可逆过程。
同理可证：如果是有耗散的过程，则一定是不可逆过程。
结论：准静态过程和无耗散是可逆过程的必要条件。
同理可证：如果是可逆过程，则一定是无耗散的准静态过程。
结论：准静态过程和无耗散是可逆过程的充分必要条件。即
准静态过程＋无耗散效应＝可逆过程
例１－８简答题：准平衡过程与可逆过程有何共同处？有何区别？有何联系？（北京科技大学考
研试题）
入可逆过程的意义
%
可逆过程进行的结果不会产生任何能量损失，理论上热功转换效率最大，可以作为实际过程中
能量转换效果比较的标准和努力的方向 。
%
不可逆因素太复杂，不容易直接去研究，而可逆过程比较简单，有助于理论上的分析研究和简化
计算。如可逆过程的功与热完全可用系统内工质的状态参数表达，可不考虑系统与外界的复杂关系，
易分析。
%
实际过程不是可逆过程，但为了研究方便，先按理想情况（可逆过程）处理，然后再根据经验，利
用修正系数或效率加以修正，得到接近于实际情况的数据。
完全可逆、内可逆与外可逆
可逆：完全可逆；内部可逆，外部不可逆（
&
常见）；外部可逆，内部不可逆；完全不可逆
例：内可逆外不可逆
—３１—
沈维道《工程热力学》考点精讲及复习思路
正确理解“等温传热”、“无压差膨胀”、“无压差压缩”等说法 。
考点５：发生热力过程的原因———功和热
①通过边界能量交换之一 ———功（ｗｏｒｋ）
功的定义
力学定义：力×在力方向上的位移
该定义的优点：具体，直观，明确。
该定义的缺点：太具体，太直观，太明确。
对“力”、“位移”要求有局限性，范围窄，“乘”的关系也太明确，这些都造成该定义适用范围窄。
例１－９：下列关于功的定义哪一个更准确？哪一个更具有普遍性？各有何适用范围？
１）功是力与距离的乘积。
２）功是物体所受的力与沿力作用方向所产生的位移的乘积。
３）功是物体所受的力与位移的点积（内积）。
４）功是物体所受的力沿力作用方向所产生的位移的积分。
５）功是其驱动力沿驱动力作用方向所移动某一路径的积分。
６）功是能转化的量度。
７）功是热力系与外界在边界上发生的一种相互作用，其唯一效果可归结为举起了一个重物。
８）功是系统与外界相互作用的一种方式，在力的推动下，通过有序运动方式传递的能量。
简单可压缩热力系的功 ———体积功的计算
体积功的计算以外界得到多少功为准，其微分表达式为
δｗ＝Ｆｄｘ＝（ｐＳＵＲＲ＋ｆ）Ａｄｘ＝（ｐＳＵＲＲ＋ｆ）ｄｖ
只有体积变化才能交换功，故称为体积变化功或体积功。
显然，只有对准静态过程，即ｐ＝ｐＳＵＲＲ以及无耗散
Ｆ＝０时，有
体积功的微分表达式δｗ＝ｐｄｖ
体积功的积分表达式ｗ＝∫
ｖ２
ｖ１
ｐｄｖ
　　　　　
—４１—
ｐ －Ｖ图上面积可以表示体积功的大小。称为示功图。ｗｏｒｋｄｉａｇｒａｍ
关于功的几点说明
１．只有可逆条件下上述体积功的表达式才适用。即只有可逆过程的功完全可以用热力系内工质
的状态参数表达，而不考虑系统与外界的复杂关系。这是可逆过程的重要意义之一。
２．ｐ－ｖ图称为示功图（ｗｏｒｋｄｉａｇｒａｍ）。显然过程１－２不同，其下的面积１２３４１也不同，说明体积
功不仅和起始点状态 １、２有关，而且还和过程有关。因此通常说体积功是一个过程量，而不是状
态量。
３．其他类型功如拉伸功，表面张力功，电功等也有类似表达式，也是过程量，也只能在可逆条件下
使用。如
δｗ弹力 ＝－σｄε　δｗ张力 ＝－σｄＡ
δｗ电 ＝Ｅｄｓ δｗ磁 ＝－μ０ΗｄＩ
４．热力学中规定，热力系对外界做功为正值；而外界对热力系做功为负值。
５．法定计量单位中功的单位为（焦耳Ｊｏｕｌｅ），即１Ｊ＝１Ｎ
#
ｍ
②通过边界能量交换之二———热（ｈｅａｔ）
热的定义
一般定义：热力系与外界之间依靠温差传递的能量称为热量。
但该定义对可逆的无温差的传热过程有逻辑矛盾，不适用。
热力学定义：一个质量不变的热力系，不做功而通过边界传递的能量称为热量 。
热力学中规定：热力系吸热时热量取正值，放热时取负值 。
热的单位
卡（或称小卡，ｃａｌｏｒｉｅ，记作ｃａｌ）的缺点：每当测量的水的比热容精确度改变时，过去的测量数据
都得改变。这种与水的比热容有关的卡称为“湿卡”。
４℃卡　　　　　　１ｃａｌ４＝４．２０５４Ｊ
１５℃卡 １ｃａｌ１５＝４．１８５５Ｊ
热化学卡 １ｃａｌｔｈ＝４．１８４０Ｊ
国际蒸汽表卡 １ｃａｌＩＴ＝４．１８６８Ｊ
ｉｎｔｅｒｎａｔｉｏｎａｌｔａｂｌｅｃａｌｏｒｉｅ
热应该采用焦耳作为其单位。用Ｊ测量热量，其精度远高于通过测量热容来测量热量的方法，可
以提高热量的测量精度。
—５１—
沈维道《工程热力学》考点精讲及复习思路
热量与体积功之比较
清华大学刘仙洲教授命名为“熵”
关于熵的说明
１．熵是状态参数
２．符号规定
系统吸热时为正　Ｑ ＞０　　　ｄＳ ＞０
系统放热时为负　Ｑ ＜０　　　ｄＳ ＜０
３．熵的物理意义：熵体现了可逆过程传热的大小与方向，是热传递的标志，是系统无序程度的
度量。
４．用途：判断热量方向和不可逆性，计算可逆过程的传热量
示功图（ｗｏｒｋｄｉａｇｒａｍ）与示热图（ｈｅａｔｄｉａｇｒａｍ）
例１－１０简述题：给出“热”和“功”的定义，并分析其异同 （北航考研试题）
考点６：热力循环（Ｔｈｅｒｍｏｄｙｎａｍｉｃｃｙｃｌｅ）
热力过程的缺陷：
仅通过一个热力过程是不可能连续不断地把吸入的热量转变为
功的。要想连续不断地获得工质的功，就必须让工质返回原态，再由
原态重新开始作功。
热力循环的定义（Ｔｈｅｒｍｏｄｙｎａｍｉｃｃｙｃｌｅ）：封闭的热力过程就称为
热力循环，简称循环（ｃｙｃｌｅ）。
—６１—
热力循环的分类（ＣｌａｓｓｉｆｉｃａｔｉｏｎｏｆｔｈｅＣｙｃｌｅｓ）
按循环的效果不同，热力循环可分为正向循环和逆向循环。
正向循环就是在循环中把热能转变为机械能的循环，所有的热力发动机（如汽车、船舶、航空动力
装置）和其它输出动力的装置（如蒸汽动力等）都是采用的这一循环，故也称为动力循环（ｐｏｗｅｒｃｙｃｌｅ
）或热机循环（ｔｈｅｒｍａｌｅｎｇｉｎｅｃｙｃｌｅ）。
逆向循环就是在循环中把机械能转变为热能的循环，所有的制冷机（如冰箱、空调等）和其它输出
热能的装置（如热泵等）都是采用的这一循环，故也称为制冷循环（ｒｅｆｒｉｇｅｒａｔｉｏｎｃｙｃｌｅ）或热泵循环
（ｈｅａｔｐｕｍｐｃｙｃｌｅ）。
正向循环 （Ｆｏｒｗａｒｄｃｙｃｌｅ）
Ｗ０ ＝Ｗ１Ａ２－Ｗ２Ｂ１ ＝∫
１Ａ２
ｐｄＶ－∫
２Ｂ１
ｐｄＶ＝∮
１Ａ２Ｂ１
ｐｄＶ
＝面积１Ａ２３４－面积２Ｂ１４３＝面积１Ａ２Ｂ１
正向循环 （Ｆｏｒｗａｒｄｃｙｃｌｅ）
吸热量Ｑ１ ＝∫
１Ａ２
Ｔｄｓ＝面积１Ａ２３４１
放热量Ｑ２ ＝∫
１Ｂ２
Ｔｄｓ＝面积１Ｂ２３４１
净吸热量Ｑ０ ＝Ｑ１－Ｑ２ ＝∫
１Ａ２
Ｔｄｓ－∫
１Ｂ２
Ｔｄｓ＝∮
１Ａ２Ｂ１
Ｔｄｓ＝面积１Ａ２Ｂ１
特点：
顺时针循环，从高温吸热，
向低温放热，从外界净输入热量
正向循环 （Ｆｏｒｗａｒｄｃｙｃｌｅ）
由热力学第一定律
—７１—
沈维道《工程热力学》考点精讲及复习思路
在正向循环中，工质从高温热源吸热在返回原态的过程中又向低温热源放热从而把净热量Ｑ０ ＝
Ｑ１－Ｑ２转换成了机械功Ｗ０称为动力循环（ｐｏｗｅｒｃｙｃｌｅ）或热机循环（ｔｈｅｒｍａｌｅｎｇｉｎｅｃｙｃｌｅ）。
循环经济性用经济指标度量。一般来说，经济指标是经济指标 ＝收益
代价
对于正向循环来说，“收益”———循环功
“代价”———吸热量Ｑ１，注意不是Ｑ０
经济性指标热效率为ηｔ＝
Ｗ０
Ｑ１
＝
Ｑ１－Ｑ２
Ｑ１
＝１－
Ｑ２
Ｑ１
＜１００％
结论：要想连续不断地得到功，热机不仅要有高温热源，还要有低温冷源，热效率ηｔ只能小于百分
之百。
逆向循环 Ｒｅｖｅｒｓｅｄｃｙｃｌｅ
吸热量Ｑ２ ＝∫
１Ａ２
Ｔｄｓ＝面积１Ａ２３４１
放热量Ｑ１ ＝∫
１Ｃ２
Ｔｄｓ＝面积１Ｃ２３４１
循环净放热量
Ｑ０ ＝Ｑ１－Ｑ２ ＝∫
１Ｃ２
Ｔｄｓ－∫
１Ａ２
Ｔｄｓ＝∮
１Ａ２Ｃ１
Ｔｄｓ
＝面积１Ｃ２３４１－面积１Ａ２３４
＝面积１Ａ２Ｃ１
特点：
逆时针循环，从低温吸热，向高温放热，向外界净放出热量Ｑ０，称为制冷循环（ｒｅｆｒｉｇｅｒａｔｉｏｎｃｙｃｌｅ）
或热泵循环（ｈｅａｔｐｕｍｐｃｙｃｌｅ）。
　　　
循环功
—８１—
Ｗ０ ＝Ｗ１Ｃ２－Ｗ１Ａ２ ＝∫
１Ｃ２
ｐｄＶ－∫
１Ａ２
ｐｄＶ＝∮
１Ａ２Ｃ１
ｐｄＶ
＝面积１Ｃ２３４－面积１Ａ２３４＝面积１Ａ２Ｃ１
特点：逆时针循环，从外净输入循环功
经济指标仍是经济指标 ＝收益
代价
对于逆向循环来说，“代价”———循环功
“收益”—随目的不同而有所不同！
制冷机“收益”—吸热量Ｑ２
制冷系数εｃ ＝
Ｑ２
Ｗ０
＝
Ｑ２
Ｑ１－Ｑ２
热泵“收益”—放热量Ｑ１
供暖系数εｗ ＝
Ｑ１
Ｗ０
＝
Ｑ１
Ｑ１－Ｑ２
＞１
结论：要想让热量从低温传向高温就必须付出代价———作功。
—９１—
沈维道《工程热力学》考点精讲及复习思路
本章应注意的问题
１．基本概念貌似简单，实则暗藏杀机。一是基本概念是考研之必考内容；二是基本概念在计算
题、证明题中也起着重要作用，万万不可藐视之。
２．对待基本概念不能机械地死记硬背，首先要理解，理解得越深越好，包括其产生的机理和方法；
其次，要与相关联的概念放在一起理解。只有将众多的概念织成一个大网，方能领悟此网的形状和功
用。反之，如果只是机械地、片面地、孤立地背诵基本概念，将导致坐井观天、见木不见林的结果，学习
效率低下。
３．基本概念的建立过程体现了工程热力学理性思维、抽象思维以及理想化方法的应用，要注意学
习和掌握，使得概念更灵活，更通用。
—０２—
第二章　热力学第一定律
本章考研要求
·熟练应用热力学第一定律解决具体问题
·深刻理解能量、储存能、热力学能的概念
·理解和掌握体积功、轴功、技术功、流动功相互间联系与区别及计算
·掌握焓的概念及其物理意义
考点一　热力学第一定律的实质
热力学第一定律的实质——— 能量转换与守恒定律
ｌａｗｏｆｅｎｅｒｇｙｃｏｎｓｅｒｖａｔｉｏｎａｎｄｃｏｎｖｅｒｓｉｏｎ
自然界的一切物质都具有能量。能量不可能被创造，也不可能被消灭，而只能在一定条件下从一
种形态转换为另一种形态。在转换过程中，能量的总和保持不变。
热力学第一定律反映了两个方面的问题：
首先，热能与其他形式的能量之间可以互相转换 ；
其次，热力学第一定律说明在转换过程中能量的数量保持不变 。
第一类永动机是不可能制造成功的 。
表达式为Ｗ＝ＡＱ
热功当量Ａ ＝４．１８６８Ｊ／ｃａｌ
热量采用与功一样的单位，都是焦耳（Ｊ），则热功当量Ａ ＝１Ｊ功／Ｊ热
表达式的缺点是：它不是针对热力系列出的，式中没有出现热力系。
对任意热力系，能量守恒方程都可以表示为：
进入热力系的能量－离开热力系的能量＝热力系储存能量的变化
考点二　热力学第一定律的基本表达式
进入闭口系的能量为热力系吸热量Ｑ
离开热力系的为热力系对外做功量Ｗ
闭口系的总储存能变化为ΔＥ＝Ｅ２－Ｅ１
则有Ｑ－Ｗ ＝ΔＥ
或写为Ｑ＝ΔＥ＋Ｗ
上式通常称为热力学第一定律的基本表达式，没有任何限制性条件。
Ｅ为储存能ΔＥ＝ΔＵ＋ΔＥｋ＋ΔＥｐ
Ｅ ＝Ｕ ＋Ｅｋ＋Ｅｐ　　ｅ＝ｕ ＋ｅｋ＋ｅｐ
Ｅｋ和Ｅｐ统称为外部储存能或宏观能量，Ｕ称为内部储存能（简称内能）或热力学能。
宏观能量：
系统工质与外力场的相互作用所具有的能量。如：重力位能Ｅｐ ＝ｍｇｚ
—１２—
沈维道《工程热力学》考点精讲及复习思路
以外界为参考坐标的系统宏观运动所具有的能量。如：宏观动能Ｅｋ ＝
１
２ｍｃ
２
Ｅｋ和Ｅｐ代表了热力系作为一个整体宏观运动所具有的机械能，与热力系内部的状态参数无关 。
考点三　热力系的储存能、热力学能
从宏观角度看，它是热力系内部工质的能量；从微观角度看，理论上它应包括组成物体的所有微
观粒子所具有的能量，与工质内部粒子的微观运动和空间位置有关，因此有时也称为微观能量。内部
储存能 ———热力学能
２．内部储存能 ———热力学能
热力学能：
分子动能（移动、转动、振动的能量）
分子位能（分子间相互作用的能量）
化学能（分子的化学键被打开释放的能量）
核能（原子核分裂或聚合成所释放出巨大能量）
……（物质无限可分所可能释放出的巨大能量）
热力学能的几点说明
∫
２
１
ｄｕ＝ｕ２－ｕ１　∮ｄｕ＝０
·热力学能是状态量
·Ｕ：广延参数　［ｋＪ］ｕ＝Ｕｍ：比参数　［ｋＪ／ｋｇ］
·热力学能总以变化量△Ｕ出现，因此零点可以任意人为确定。而且如果对未参与热力过程的
能量，其能量在热力过程中不会有任何变化，也就不会对热力过程产生任何影响。因此在热力学中通
常只计算那些参与了热力过程的能量。如果热力过程涉及到更细微的粒子的能量，则热力学能还应
该包括这些更深层次的、更强大的、甚至目前尚未发现的新形式的能量。所以，尽管热力学能的范围
很广，我们没有必要也不可能去计算它的绝对值。
·对简单可压缩热力系，有两个独立的自变量，则
Ｕ＝Ｕ（Ｔ，Ｖ）＝Ｕ（Ｔ，ｐ）　ｕ＝Ｕｍ ＝ｕ（Ｔ，ｖ）＝ｕ（Ｔ，ｐ）
ｄｕ＝（）ｄＴ＋（）ｄｖ　
２ｕ
Ｔｖ
＝ 
２ｕ
ｖＴ
·对理想气体，忽略其分子间力，也就忽略了分子势能，在没有化学反应及核反应的条件下，有ｕ
＝ｆ（Ｔ），即理想气体的热力学能仅与温度有关。
·固体和液体的体积不变，分子间距离不变，热力学能可以只包括分子动能，不包括分子势能，则
其热力学能仅与温度有关，与体积无关，即ｕ ＝ｆ（Ｔ）
·由于温度是大量分子热运动平均动能的度量，因此分子动能能量变化会引起温度的变化，通常
称为显能，显能释放就成为显热；而分子势能不会引起温度的变化，因而通常称为潜能，潜能释放出来
就是通常所说的潜热。
—２２—
·给固体或液体加热时 ，其分子运动克服其分子间力的束缚，分子间距离拉大，发生向液体或气
体的转变，即相变。这时吸热全部变为潜能增加，而温度不变，显能不变，如从固态变为液态时的熔解
潜热和液态变气态时的汽化潜热等等。显然，在相变的时候需要考虑固体和液体的分子势能而不需
要考虑固体和液体的分子动能。ｕ ＝ｆ（ｖ）
４．内部储存能和外部储存能的区别
·内部储存能和外部储存能虽然都是能量的储存方式，但它们的性质是截然不同的。
·外部储存能是热力系的所有分子向着同一个方向运动所具有的宏观动能，其特点是所有分子
向着同一个方向的有序运动，因此通常也称为有序能（ｏｒｇａｎｉｚｅｄｅｎｅｒｇｙ）
·热力学能是由大量分子的微观无序运动所具有的能量（即微观能量），其特点是无序运动，故也
称为无序能（ｄｉｓｏｒｇａｎｉｚｅｄｅｎｅｒｇｙ）
ｏｒｇａｎｉｚｅｄｅｎｅｒｇｙ
·有序能可以直接做功，而无序能却不能，必须转变为有序能才能做功；有序能可以百分之百地
转变为无序能，而无序能却不能百分之百地转变为有序能，它们的地位明显是不相等的！
·工程热力学研究功———热之间的转换，其本质就是有序运动与无序运动之间的转换。正是有
序与无序之间的本质差别，造成了这种转换的特殊困难与限制。
考点四　闭口系能量方程
系统总能
Ｅ ＝Ｕ ＋Ｅｋ ＋Ｅｐ
ｅ＝ｕ ＋ｅｋ＋ｅｐ
ΔＥ＝ΔＵ＋ΔＥｋ＋ΔＥｐ
如果真在地球上研究飞行器内部热力系
$
ｑ ＝ｄｅ＋
$
ｗ ＝ｄｕ ＋ｄｅｋ＋ｄｅｐ＋$
ｗ
通常把坐标系选在固定在热力系上，这时观察者随热力系一起运动时，看不到热力系宏观动能和
位能的变化。则有
ΔＥｋ ＝ΔＥｐ ＝０　Ｅ ＝Ｕ 　ｅ＝ｕ
—３２—
沈维道《工程热力学》考点精讲及复习思路
闭口系能量方程
Ｑ＝ΔＵ＋Ｗ　δＱ＝ｄＵ＋δＷ
ｑ＝Δｕ＋ｗ　δｑ＝ｄｕ＋δｗ
该式是德国的克劳修斯（ＲｕｄｏｆＣｌａｕｓｉｕｓ，１８２２—１８８８）在１８５０年首先提出的 。
功 （ｗ）是广义功
$
ｗ ＝
$
ｗ 体积 ＋$
ｗ 拉伸 ＋$
ｗ 张力 ＋
…．．．
体积变化功　　　　　　
$
ｗ 体积 ＝ｐｄｖ
拉伸功　　　
$
ｗ 拉伸 ＝ －σｄε
表面张力功　　　
$
ｗ 张力 ＝ －σｄＡ
简单可压缩热力系可逆过程
$
ｑ ＝ｄｕ ＋ｐｄｖ　　　　　热一律第一表达式
Ｔｄｓ＝ｄｕ ＋δｗ
简单可压缩热力系任意过程
Ｔｄｓ＝ｄｕ ＋ｐｄｖ　热一律第一解析式
'
Ｔｄｓ＝
(
ｕ ＋
'
ｐｄｖ
考点五　闭口系的有用功和无用功
闭口系必须挤压大气环境才能获得其体积，这部分功不能被直接使用，属于无用功，它是闭口系
在空间能够存在所必需付出的代价，或者说是必要条件。其表达式为
δＷｕ ＝ｐ０ｄＶ
则净有用功为δＷｅ＝δＷ－δＷｕ ＝δＷ－ｐ０ｄＶ
考点六　开口系能量方程与焓
工程上用的绝大多数设备都伴随有工质的流进流出，如内燃机、燃气轮机、压气机、锅炉、风机、换
热器、管道内流动等等，因而都可以作为开口系来处理。实际上，真正能够当作闭口系的热力系在工
程上几乎没有。
把参数只沿流动方向变化的流动称为一维流动或一元流动（Ｏｎｅ－ｄｉｍｅｎｓｉｏｎａｌｆｌｏｗ）。
一维流动的优点：简单，实用，突出了开口系的主要矛盾
一维流动———建立的物理模型。
１．质量守恒———连续方程 ｃｏｎｔｉｎｕｉｔｙｅｑｕａｔｉｏｎ
对开口系来说，要遵守的第一个定律就是质量守恒原理。
ｍｉｎ－ｍｏｕｔ＝ΔｍＣＶ
ｑｍ，ｉｎ－ｑｍ，ｏｕｔ＝
ｄｍＣＶ
ｄτ
ｑｍ，ｉｎ ＝
δｍｉｎ
ｄτ
　ｑｍ，ｏｕｔ＝
δｍｏｕｔ
ｄτ
—４２—
２．能量守恒———开口系一般瞬态能量方程
１）流动功（或推动功）ｆｌｏｗｗｏｒｋ
为推动流体通过热力系界面而传递的机械功。
设进口截面积为Ａ１，具有体积Ｖ１的工质ｍ １由外界恰好移入热力系，其平移距离为ｘ１，则由图知
流动功为Ｗｆ１ ＝ｐ１Ａ１ｘ１ ＝ｐ１Ｖ１ ＝ｍ１ｐ１ｖ１
１）流动功（或推动功）
写作功率的形式：Ｗｆ１

＝
δＷｆ１
ｄτ
＝
δｍ１
ｄτ
ｐ１ｖ１ ＝ｑｍ１ｐ１ｖ１
或写作比功的形式：ｗｆ１ ＝
δＷｆ１
ｄｍ ＝ｐ１ｖ１
在出口，热力系只有对工质做功才能把它推出热力系，该流动功为：
Ｗｆ２ ＝ｐＳＵＲＲ２Ａ２ｘ２ ＝ｐＳＵＲＲ２Ｖ２ ＝ｍ２ｐＳＵＲＲ２ｖ２
只有对可逆过程有：ｐ２ ＝ｐＳＵＲＲ２
因此只有可逆时有：Ｗｆ２ ＝ｐ２Ｖ２ ＝ｍ２ｐ２ｖ２
在整个流动过程中热力系对外做的净流动功为进、出口之差，为
Ｗｆ＝Ｗｆ２－Ｗｆ１ ＝ｐ２Ｖ２－ｐ１Ｖ１ ＝ｍ２ｐ２ｖ２－ｍ１ｐ１ｖ１
流动功的特点
①它是工质发生穿越热力系边界的宏观移动时与外界所交换的功，在移动过程中工质的状态并
没有改变，只是工质的位置发生了变化。
②它是一个与宏观流动有关的功。
③由于开口系都存在流动，因此，开口系都伴随有流动功，或者说流动功是开口系存在的必要
条件。
④体积功是过程量，流动功只取决于工质进出口的状态，不是过程量。有时也把它称为流动能或
—５２—
沈维道《工程热力学》考点精讲及复习思路
输运能；
ｆｌｏｗｅｎｅｒｇｙ，ｃｏｎｖｅｃｔｅｄｅｎｅｒｇｙ，ｔｒａｎｓｐｏｒｔｅｎｅｒｇｙ
⑤流动功随工质进出热力系，一定程度上具有能量的性质，但却不是工质本身所具有的能量，一
般认为它是工质所携带的能量。
２）开口系一般瞬态能量方程
能量守恒：ｅｎｅｒｇｙｃｏｎｓｅｒｖａｔｉｏｎ
进入系统的能量－离开系统的能量＝系统储存能量的变化
进入ＣＶ的能量
＝Ｑ＋Ｅｉｎ
＝Ｑ＋ｍｉｎ（ｅ
＝Ｑ＋ｍｉｎ（ｕ
离开ＣＶ的能量
＝ＷＣＶ＋Ｅｏｕｔ
＝Ｗｎｅｔ＋ｍｏｕｔ（ｅ
＝Ｗｎｅｔ＋ｍｏｕｔ（ｕ
开口系ＣＶ储存能量的变化＝ΔＥＣＶ ＝Ｅ２－Ｅ１
流动时，总在一起出现
　　 Ｑ ＋　ｍ ｉｎ（ｕ ＋ｐｖ＋ｃｆ
２／２＋ｇｚ）ｉｎ－ｍ ｏｕｔ（ｕ ＋ｐｖ＋ｃｆ
２／２＋ｇｚ）ｏｕｔ　 －Ｗ ｎｅｔ＝△Ｅｃｖ
开口系从外界吸收的热量，一部分用来使开口系自身能量增加，一部分用来对外做功，最后一部
分用来支付由于工质进出开口系带出和带入能量的差，包括热力学能、流动功、宏观动能和宏观位能。
Ｑ ＝ΔＥｃｖ＋ｍ ｏｕｔ（ｈ ＋ｃｆ
２／２＋ｇｚ）ｏｕｔ－ｍ ｉｎ（ｈ ＋ｃｆ
２／２＋ｇｚ）ｉｎ＋Ｗ ｎｅｔ
δＱ＝ｄＥＣＶ＋δｍｏｕｔ（ｈ＋
ｃ２ｆ
２＋ｇｚ）ｏｕｔ
－δｍｉｎ（ｈ＋
ｃ２ｆ
２＋ｇｚ）ｉｎ
＋δＷｎｅｔ
Ｑ
·
＝ｄＥｃｖ／δτ＋ ｈ＋ｃ２ｆ／２( )＋ｇｚｏｕｔｑｍ，ｏｕｔ－ ｈ＋ｃ２ｆ／２( )＋ｇｚｉｎｑｍ，ｉｎ＋Ｗ
·
ｎｅｔ
常用流率Ｑ
·
＝ｌｉｍ
δτ→０
δＱ( )δτｑｍ ＝ｌｉｍδτ→０ δｍ( )δτ　Ｗ

ｎｅｔ＝ｌｉｍ
δτ→０
δＷｎｅｔ( )δτ
当有多股进出口时：
—６２—
Ｑ
·
＝
ｄＥＣＶ
ｄτ
＋∑
ｏｕｔ
ｑｍ，ｏｕｔ（ｈ＋
ｃ２ｆ
２＋ｇｚ）ｏｕｔ
－∑
ｉｎ
ｑｍ，ｉｎ（ｈ＋
ｃ２ｆ
２＋ｇｚ）ｉｎ
＋Ｗ
·
ｎｅｔ
焓（Ｅｎｔｈａｌｐｙ）
焓的定义：焓＝热力学能＋流动功
对于ｍ千克工质：Ｈ＝Ｕ＋ｐＶ　　　　　ｋＪ　　 广延量状态参数
对于１千克工质：　ｈ＝Ｈ／ｍ＝ｕ＋ｐｖ　　ｋＪ／ｋｇ　比焓
焓的物理意义：
１．对流动工质（开口系），表示随工质进出开口系所转移的能量 。
２．对不流动工质（闭口系），焓只是一个复合状态参数。不代表任何东西。
开口系的净功Ｗｎｅｔ
定义：开口系对外做的功，由于不必克服大气压力做功，因此该功也就是净功（ｎｅｔｗｏｒｋ）或有
用功。
开口系对外做的功也来自于体积功。体积功是简单可压缩热力系所有功的源泉。
ｓｉｍｐｌｅｃｏｍｐｒｅｓｓｉｂｌｅｓｙｓｔｅｍ
在简单可压缩热力系中一般净功以推动旋转轴旋转的方式输出，因此通常也称为轴功Ｗ Ｓ
（ｓｈａｆｔｗｏｒｋ），即Ｗ ｎｅｔ＝Ｗ Ｓ
简单可压缩热力系开口系一般瞬态能量方程可以重写为
δＱ＝ｄＥＣＶ＋δｍｏｕｔ（ｈ＋
ｃ２ｆ
２＋ｇｚ）ｏｕｔ
－δｍｉｎ（ｈ＋
ｃ２ｆ
２＋ｇｚ）ｉｎ
＋δＷｓ
开口系的总能量变化ΔＥＣＶ
ΔＥＣＶ ＝
１
２（ｍＣＶ２ｃ
２
ｆ２－ｍＣＶ１ｃ
２
ｆ１）＋（ｍＣＶ２ｇｚ２－ｍＣＶ１ｇｚ１）＋（ｍＣＶ２ｕ２－ｍＣＶ１ｕ１）
若忽略开口系外部储存能的变化，则有ΔＥＣＶ ＝（ｍＣＶ２ｕ２－ｍＣＶ１ｕ１）
写作微分式ｄＥＣＶ ＝ｄ（ｍｕ）ＣＶ
简单可压缩热力系开口系一般瞬态能量方程可写为
δＱ＝ｄ（ｍｕ）ＣＶ＋δｍｏｕｔ（ｈ＋
ｃ２ｆ
２＋ｇｚ）ｏｕｔ
－δｍｉｎ（ｈ＋
ｃ２ｆ
２＋ｇｚ）ｉｎ
＋δＷｓ
３．一维稳定流动能量方程
所谓稳定流动（ＳｔｅａｄｙＳｔａｔｅＳｔｅａｄｙＦｌｏｗ），就是指开口系内空间各点参数都不随时间变化的
流动。
稳定流动条件：
—７２—
沈维道《工程热力学》考点精讲及复习思路
①进出口流量相等ｑｍ，ｏｕｔ＝ｑｍ，ｉｎ ＝ｑｍ
②每截面状态不变ｄＥＣＶ／δτ＝０
Ｑ
·
＝ｄＥｃｖ／δτ＋ ｈ＋ｃ２ｆ／２( )＋ｇｚｏｕｔｑｍ，ｏｕｔ－ ｈ＋ｃ
２
ｆ／２( )＋ｇｚｉｎｑｍ，ｉｎ＋Ｗ
·
ｎｅｔ
Ｑ
·
＝ｑｍ ｈ＋
ｃ２ｆ
２( )＋ｇｚ
ｏｕｔ
－ ｈ＋
ｃ２ｆ
２( )＋ｇｚ[ ]
ｉｎ
＋Ｗ
·
ｓ
Ｑ
·
＝ｑｍｑ　　　　Ｗ
·
ｓ＝ｑｍｗｓ
对微元过程
δｑ＝ δＱδｍｉｎ
＝ δＱ
δｍｏｕｔ
＝ｄｈ＋ｄ
ｃ２ｆ
２＋ｇｄｚ＋δｗｓ
对积分过程ｑ＝
ｑｍ ＝Δｈ＋１２Δｃ
２
ｆ＋ｇΔｚ＋ｗｓ
稳定流动能量方程ｑ＝Δｈ＋１２Δｃ
２
ｆ＋ｇΔｚ＋ｗｓ
方程表明：稳定流动中，对开口系的加热量一部分使工质焓增加，另一部分使工质的宏观动能和
宏观位能增加，并对外输出轴功。
适用条件：任何流动工质、任何稳定流动过程
４．热力学第一定律开口系表达式
１
２Δｃ
２
ｆ＋ｇΔｚ＋ｗｓ＝ｗｔ
热力学第一定律第二表达式（限制条件：稳定流动 ）：
对微元过程δｑ＝ｄｈ＋δｗｔ
对积分过程ｑ＝Δｈ＋ｗｔ
思考：热力学第一定律第一表达式
$
ｑ＝ ｄｕ＋
$
ｗ为何没有条件限制？
几种功之间的关系
ｗｔ＝
１
２Δｃ
２
ｆ＋ｇΔｚ＋ｗｓ
ｑ＝Δｈ＋ｗｔ＝Δｕ＋Δ（ｐｖ）＋ｗｔ
ｑ＝Δｕ＋ｗ　ｗ＝Δ（ｐｖ）＋ｗｔ＝ｗｆ＋ｗｔ
ｓｉｍｐｌｅｃｏｍｐｒｅｓｓｉｂｌｅｓｙｓｔｅｍ
简单可压缩热力系功的源泉
ｗ
ｗｔ（△ｃｆ
２／２、ｇ△ｚ）
ｗｆ＝△（ｐｖ）
结论：简单可压缩热力系的技术功、流动功、轴功，等等，都来自于体积功。体积功是简单可压缩
热力系功的唯一源泉。
技术功的表达式Ｔｅｃｈｎｉｃａｌｗｏｒｋ
若过程可逆，则
—８２—
δｗｔ＝δｗ－δｗｆ＝ｐｄｖ－ｄ（ｐｖ）
　　 ＝ｐｄｖ－（ｐｄｖ＋ｖｄｐ）＝－ｖｄｐ
δｗｔ＝－ｖｄｐ　ｗｔ＝－∫ｖｄｐ　条件：可逆
可逆条件下
δｑ＝ｄｕ＋ｐｄｖ热一定律第一解析式
δｑ＝ｄｈ－ｖｄｐ热一定律第二解析式
技术功表达式的几点说明
ｗｔ＝－∫ｖｄｐ
１．与体积功表达式不同的是：技术功是因压力变化而做的功，压力下降，对外做功；压力上升，外
界对热力系做功。因此通常也称为“压力功”。
２．开口系对外输出的技术功是压力功而非体积功，两者相差一个流动功。
３．工质的比体积越小，为提高工质压力所消耗的技术功就越小；而工质的比体积越大，在同样的
压差下工质膨胀对外所做的技术功就越大。
开口系减少耗功增大做功的例子
在水蒸气动力循环就是采用这一原理来获得尽可能大的净功的。这也是瓦特发明冷凝器将膨胀
做功后的水蒸气先冷凝为液体再用水泵打回锅炉，从而提高了蒸汽机热效率的具体原因。
技术功在示功图上的表示
－∫ｖｄｐ＝∫ｐｄｖ＋ｐ１ｖ１－ｐ２ｖ２
ｗｔ＝ｗ＋ｐ１ｖ１－ｐ２ｖ２
ｗｔ＝ｗ－Δ( )ｐｖ
ｗｔ＋Δ( )ｐｖ＝ｗ
—９２—
沈维道《工程热力学》考点精讲及复习思路
５．机械能或动量守恒———伯努利方程
可逆条件下，将δｗｔ＝－ｖｄｐ代入技术功定义式，得
－ｖｄｐ＝ｄ
ｃ２ｆ
２＋ｇｄｚ＋δｗｓ伯努利方程Ｂｅｒｎｏｕｌｉｅｑｕａｔｉｏｎ
反映了机械能守恒关系（ｃｏｎｓｅｒｖａｔｉｏｎｏｆｍｅｃｈａｎｉｃｅｎｅｒｇｙ）。
伯努利方程δｗｔ＝－ｖｄｐ＝ｄｃ
２
ｆ／２＋ｇｄｚ＋δｗｓ
对于流体流过管道，δｗｓ＝０
ｖｄｐ＋１２ｄｃ
２
ｆ＋ｇｄｚ＝０
压力能　　动能　 位能 →伯努利方程的机械能守恒形式
ｄｐ
ρｇ
＋１２ｇｄｃ
２
ｆ＋ｄｚ＝０对不可压流动（ｉｎｃｏｍｐｒｅｓｓｉｂｌｅ），积分得
ｐ１
ρｇ
＋１２ｇｃ
２
ｆ，１＋ｚ１ ＝
ｐ２
ρｇ
＋１２ｇｃ
２
ｆ，２＋ｚ２原始伯努利方程形式
瑞士数学家伯努利（ＤａｎｉｅｌＢｅｒｎｏｕｌｉ１７００～１７８２）在１７３８年提出的
－ｄｐ－ρｇｄｚ－ρδｗｓ＝ρｃｆｄｃｆ
伯努利方程的牛顿第二定律或动量方程形式
伯努利方程的误区一：适用条件“绝热”
伯努利方程的误区二：“压力能”的概念
三方程之间的关系
δｑ＝ｄｈ＋δｗｔ
热力学第一定律 　热量→焓＋技术功
伯努利方程 　δｗｔ＝－ｖｄｐ＝ｄｃ
２
ｆ／２＋ｇｄｚ＋δｗｓ
技术功→宏观动能＋宏观位能＋轴功
一维稳定流动能量方程δｑ＝ｄｈ＋ｄ
ｃ２ｆ
２＋ｇｄｚ＋δｗｓ
热量→焓＋宏观动能＋宏观位能＋轴功
结论：三个方程中只有两个是独立的。
秘笈：不仅要记住方程本身，还要记住其使用条件，以及各个方程之间的相互关系。就是要理解
其推导过程。
考点七　能量方程的工程应用
热力学第一定律貌似容易，实际上应用起来也还是有一定难度的。
难度一：无公式可套，应用灵活。
难度二：不会选择热力系。
１．透平机械 ｔｕｒｂｏｍａｃｈｉｎｅｒｙ
—０３—
透平机械是将热能转变为机械功并向外输出的旋转机械设备，也简称透平（Ｔｕｒｂｉｎｅ）或涡轮。
数学模型 ｑ≈０→ｗｔ＝－Δｈ＝ｈ１－ｈ２
忽略宏观位能和宏观动能ｇΔｚ≈０　 １２Δｃ
２
ｆ≈０
ｗｓ＝ｈ１－ｈ２
这是一个将工质（如水蒸气或燃气）内热能（ｈ）转变为对外输出轴功（ｗｓ）的热力过程。
２．压缩机械 ｃｏｍｐｒｅｓｓｏｒ
用来压缩气体使气体压力升高的设备称为压缩机械 。
数学模型 －ｗｔ＝Δｈ－ｑ＝（ｈ２－ｈ１）－ｑ
忽略宏观位能和宏观动能ｇΔｚ≈０　 １２Δｃ
２
ｆ≈０
－ｗｓ＝ｈ２－ｈ１－ｑ
这是一个将外界输入轴功（－ｗｓ）转变为工质（如空气）内热能（ｈ）的热力过程。
若压缩过程可逆，则∫ｖｄｐ＝（ｈ２－ｈ１）－ｑ
３．喷管和扩压管 Ｎｏｚｚｌｅ＆Ｄｉｆｕｓｅｒ　
物理模型
绝热与绝（轴）功流动，或就简称为绝能流动 （ａｄｉａｂａｔｉｃｆｌｏｗ）。
数学模型
ｑ≈０，ｗｓ＝０→
１
２（ｃ
２
ｆ２－ｃ
２
ｆ１）＝－Δｈ＝ｈ１－ｈ２
喷管：工质在内流动中会以自身的焓降使宏观动能增加，以获得较高的出口速度 。
扩压管：工质在内流动中以自身速度的下降使焓增加。
若过程可逆，则∫ｖｄｐ＝（ｈ２－ｈ１）＝１２（ｃ２ｆ１－ｃ２ｆ２）
４．换热器 ｈｅａｔｅｘｃｈａｎｇｅｒ
利用冷热流体的温差将热量由热流体传递给冷流体的设备称为换热器 （Ｈｅａｔ　Ｅｘｃｈａｎｇｅｒ）。
２种数学模型：ｑｍ１（ＣＶ１）或ｑｍ２（ＣＶ２）和ｑｍ１（ＣＶ１）＋ｑｍ２（ＣＶ２）
选取ｑｍ１（ＣＶ１）或ｑｍ２（ＣＶ２）为热力系ｗｓ＝０
忽略宏观位能和宏观动能ｇΔｚ≈０，１２Δｃ
２
ｆ≈０
则ｗｔ＝０→ｑ＝ｈ２－ｈ１
工质在被加热（冷却）过程中得到（失去）的热量等于其焓的增加（减少）
—１３—
沈维道《工程热力学》考点精讲及复习思路
取ｑｍ１（ＣＶ１）＋ｑｍ２（ＣＶ２）为热力系ｗｓ＝０，ｑ≈０
忽略宏观位能和宏观动能ｇΔｚ≈０，１２Δｃ
２
ｆ≈０
则ｗｔ＝０→Ｈ２ ＝Ｈ１
（ｑｍ１ｈ２＋ｑｍ２ｈ２＇）－（ｑｍ１ｈ１＋ｑｍ２ｈ１＇）＝０
ｑｍ１（ｈ１－ｈ２）＝ｑｍ２（ｈ２＇－ｈ１＇）
冷流体的焓增等于热流体的焓降。表明热能由热流体转移到了冷流体 。５．绝热节流　ａｄｉａｂａｔｉｃ
ｔｈｒｏｔｌｉｎｇｐｒｏｃｅｓｓ
工质在管内流过阀门、孔板、小孔等使流通截面突然缩小的装置时，会在缩口附近产生强烈旋涡，
从而产生所谓“局部阻力”，使压力下降。这种现象称为节流。
由于节流过程进行得很快，工质的散热量与其所携带的能量相比很小，通常予以忽略，因而称之
为绝热节流 （ａｄｉａｂａｔｉｃｔｈｒｏｔｌｉｎｇｐｒｏｃｅｓｓ）。
物理模型：绝热绝（轴）功→绝能流动
数学模型：
ｗｓ＝０，ｑ＝０
忽略宏观位能和宏观动能
ｇΔｚ≈０，１２Δｃ
２
ｆ≈０
则ｗｔ＝０→△ｈ ＝０，ｈ１＝ｈ２
绝热节流前后工质的焓不变。
注意事项：
（１）它是一个典型的非准静态过程或非平衡过程。
（２）只能把上游进口截面１－１和下游出口截面２－２设置在远离缩孔的地方，才能用状态参数来
描述。
（３）ｈ１＝ｈ２并不表明绝热节流是一个定焓过程，因为在这个过程中焓并没有一直保持恒定不变，
而仅仅是在进出口处相等。
６．绝热混合过程
物理模型：
两种以上工质混合。由于混合过程进行得很快，工质的散热量与其所携带的能量相比很小，通常
予以忽略，因而称之为绝热混合过程（ａｄｉａｂａｔｉｃｍｉｘｉｎｇｐｒｏｃｅｓｓ）
闭口系混合
—２３—
　　　
数学模型
取整个闭口系为热力系
Ｑ ＝０，Ｗ ＝０，则△Ｕ ＝０
闭口系工质绝热混合前后热力系的热力学能保持不变。即
ｍＮ２ｕＮ２＋ｍＨ２ｕＨ２ ＝（ｍＮ２＋ｍＨ２）ｕＮ２＋Ｈ２
则ｕＮ２＋Ｈ２ ＝
ｍＮ２ｕＮ２＋ｍＨ２ｕＨ２
ｍＮ２＋ｍＨ２
对于ｎ种不同工质在闭口系中的混合，混合后的热力学能为ｕ２ ＝
∑
ｎ
ｉ＝１
ｍｉｕｉ
∑
ｎ
ｉ＝１
ｍｉ
数学模型
Ｑ ＝０、Ｗ ｔ＝０则△Ｈ ＝０
开口系工质绝热混合前后热力系的焓保持不变。即ｑｍ，Ｎ２ｈＮ２＋ｑｍ，Ｈ２ｈＨ２ ＝（ｑｍ，Ｎ２＋ｑｍ，Ｈ２）ｈ２
则ｈ２ ＝
ｑｍ，Ｎ２ｈＮ２＋ｑｍ，Ｈ２ｈＨ２
ｑｍ，Ｎ２＋ｑｍ，Ｈ２
对于多种不同工质在开口系中的混合，混合后焓为ｈ２ ＝
∑
ｎ
ｉ＝１
ｑｍ，ｉｈｉ
∑
ｎ
ｉ＝１
ｑｍ，ｉ
７．充放气过程 ｃｈａｒｇｉｎｇａｎｄｄｉｓｃｈａｒｇｉｎｇｐｒｏｃｅｓｓ
充气过程或充有气体的容器的放气过程就是一个典型的非稳定流动过程（ｕｎｓｔｅａｄｙｆｌｏｗ，ｔｒａｎｓｉｅｎｔ
—３３—
沈维道《工程热力学》考点精讲及复习思路
ｆｌｏｗ）。
均匀状态定态流动过程（ｕｎｉｆｏｒｍ－ｆｌｏｗｐｒｏｃｅｓｓ）：通过容器边界进入容器的气体进口状态不随
时间变化的充气过程。
Ｑ ＝ΔＥｃｖ＋ｍ ｏｕｔ（ｈ ＋ｃｆ
２／２＋ｇｚ）ｏｕｔ－ｍ ｉｎ（ｈ ＋ｃｆ
２／２＋ｇｚ）ｉｎ＋Ｗ ｎｅｔ
忽略动能和位能
充气 　 ΔＥｃｖ＝ｍ ｉｎ（ｈ ＋ｃｆ
２／２＋ｇｚ）ｉｎ→ΔＵ ｃｖ＝ｍ ｉｎ（ｈ）ｉｎ
放气 　 ΔＥｃｖ＝－ｍ ｏｕｔ（ｈ ＋ｃｆ
２／２＋ｇｚ）ｏｕｔ
例２－１　如图所示为一储气罐，其内部为真空，现连接于输气管道进行充气。假设充气过程进行
得很快，储气罐内部气体来不及与外界交换热量。而且输气管道所连接的气源很大，以至对储气罐的
充气对气源内部的状态几乎没有影响，输气管道内部气体的状态一直保持不变，其焓为
解法１：
（１）物理模型 这个题目要求的是罐内最后的状态参数（热力学能Ｕ２），所以我们只能取储气罐为
热力系，这是一个开口系。而且由于工质只进不出，开口系内部工质质量会随充气过程的进行逐渐增
大，压力等参数也逐渐增大。因此，这是一个典型的瞬态问题。好在按题意工质的进口参数是一个固
定的、确定的值ｈ１，因此进口能量就确定了，开口系又无对外做功和换热，按照热力学第一定律，很容
易求得开口系内部的总能量Ｕ２。
（２）数学模型　如前分析，描述这个开口系的一定是质量守恒方程和一般瞬态能量方程。
质量守恒　 　ｍ－０＝ｍＣＶ２　　　 （１）
能量守恒　　０＝（ｍＣＶ２ｕ２－０）＋０（ｈ＋
１
２ｃ
２
ｆ＋ｇｚ）
ｏｕｔ
－ｍ（ｈ＋１２ｃ
２
ｆ＋ｇｚ）
ｉｎ
＋０　（２）
忽略充气口气体的宏观动能和宏观位能，（ｈ＋１２ｃ
２
ｆ＋ｇｚ）
ｉｎ
＝ｈ１　（３）
（３）方程求解　 联立（１）（２）（３）很容易得到ｕ２ ＝ｈ１、Ｕ２ ＝ｍ２ｕ２ ＝ｍｈ１
（４）讨论及结论 结果说明：储气罐内最后的热力学能就等于随工质输入的焓。反映了焓的物理
意义：即代表了开口系中随工质转移的能量，最后把这个能量全部转换为储气罐内部气体的热力学
能。储气罐内气体这时也可以计算出一个焓值Ｈ ２＝Ｕ ２＋ｐＶ，但该焓值对于停留在储气罐内部的气
—４３—
体来说没有意义。热力系内部工质的能量完全是用热力学能来表征的。
解法２：
（１）物理模型 该题比较简单，也可以不用较为复杂的开口系一般瞬态能量方程，而
采用我们更为熟悉的闭口系方法。
（２）数学模型及求解取将要进入（状态１）及已进入储气罐的气体（状态２）整体为研究对象，则该
热力系为一闭口系。对该闭口系有ΔＵ＝ｍ２ｕ２－ｍ１ｕ１ ＝ｍｕ２－ｍｕ１
Ｑ＝０、Ｗ ＝ｐ１［Ｖ－（Ｖ＋Ｖ１）］＝－ｐ１Ｖ１ ＝－ｍｐ１ｖ１
代入闭口系能量方程，得ΔＵ＝Ｑ－Ｗ ＝０＋ｍｐ１ｖ１ ＝ｍｐ１ｖ１
Ｕ２ ＝ｍｕ２ ＝ｍｕ１＋ΔＵ＝ｍｕ１＋ｍｐ１ｖ１ ＝ｍ（ｕ１＋ｐ１ｖ１）＝ｍｈ１
３．讨论及结论
结果说明：殊途同归。开口系与闭口系只是方法的不同，其反映的物理本质是完全一样的，都是
热力学第一定律，只是在做题中怎么建立物理模型和数学模型的问题。
例２－２　在炎热的夏天，有人试图用关闭厨房门窗和打开电冰箱门的办法使厨房降温。开始他
感到很凉爽，但过一段时间后这种效果逐渐消失，甚至会感到更热，这是为什么？试分析之。
答：取包括空气、电冰箱在内的厨房为热力系对该热力系用热力学第一定律，有Ｑ＝ ΔＵ ＋Ｗ
忽略厨房向外界的散热，即　Ｑ ＝０
冰箱从外界输入电功Ｗ
$
０
则有　　　　　ΔＵ＝Ｑ－Ｗ＝－Ｗ ＞０
讨论与结论：电冰箱之所以能够制冷，是选择了冰箱为热力系的结果。如果选择了厨房为热力
系，则冰箱就与一个电炉没什么两样。该例说明了选择热力系对于热力学分析的重要性，选择热力系
是进行热力学分析的先决条件。
例２－３　汽缸内储有完全不可压缩的流体，汽缸的一端被封闭，另一端是活塞。汽缸是静止的，
与外界无热交换。试问：
１）活塞能否对流体做功？
２）流体压力会改变吗？
３）若使用某种方法把流体压力从０．２ＭＰａ提高到４ＭＰａ，热力学能有无变化？焓有无变化？流体
与外界是否有体积功的交换？是否有技术功的交换？
答：１）由于流体的体积不会改变，δＷ ＝ｐｄＶ ＝０，所以活塞不能对流体做体积功。
—５３—
沈维道《工程热力学》考点精讲及复习思路
２）当活塞压缩流体时，流体的压力会增加。
３）若将流体压力从０．２ＭＰａ提高到４ＭＰａ，此时由于流体的体积未改变，体积功Ｗ ＝０，假设汽缸
绝热，Ｑ ＝０，则由热力学第一定律知 ΔＵ＝Ｑ－Ｗ ＝０，即热力学能没有变化。但由于压力升高，技术
功 δＷ ｔ＝－ｖｄｐ ＜０，则由热力学第一定律知 ｄＨ ＝δＱ －δＷ ｔ＞０，即焓增加。
讨论及结论：该例说明，由于热力学涉及到的功的种类繁多，如体积功、技术功、轴功、流动功，甚
至电功、磁功、张力功、弹力功，等等，当分析做功时，一定要明确是什么功。不做体积功并不意味着不
做其他功。该例中活塞压缩流体不做体积功，却做技术功，说明技术功的确是与体积功不同的。实际
上即使有技术功输入，也不意味外界真正会耗费能量。因为技术功、焓等概念是对开口系建立的，只
有对开口系才有意义。在本例中，由于流体是被活塞封闭在汽缸内的，属于闭口系，并没有流体真正
跨过边界进入汽缸，所以该流动功并不会真正起作用，技术功也就不会真正起作用，外界也就不用真
正耗费能量。计算得到的技术功或焓只是意味着：一旦有流体进入或排出汽缸，这些流体将与外界交
换更多的功，焓也将发生更大的变化。所以，对于各种不同的功、焓等概念，一定要有深刻的理解。
例２－４　说明下列说法是否正确，并说明原因：
（１）气体膨胀时，一定对外做功。
（２）气体压缩时，一定消耗外功。
（３）压力下降时，一定对外做轴功。
（４）压力升高时，外界一定消耗轴功。
（５）工质进行膨胀时，一定从外界吸热。
（６）工质吸热时，热力学能一定增加。
（７）工质从外界吸热时，一定膨胀。
（８）热力学能增加时，温度一定增加。
（９）工质吸热时，温度一定增加。
（１０）提高液体的压力比提高气体的压力容易。
（１１）气体的做功能力比液体强。
（１２）熵增加时，一定吸热。
例２－４　说明下列说法是否正确，并说明原因：
（１）气体膨胀时，一定对外做功。
答：不一定。如果这个功指的是体积功，则要看是否可逆。如果是可逆过程，则δＷ ＝ｐｄＶ ＞０，
即一定对外做功。如果是不可逆过程，不能使用 δＷ ＝ｐｄＶ计算体积功，而只能采用更基本的公式
δＷ＝ｐｄＶ来计算，对外界为真空的情况，由于ｐｓｕｒｒ＝０，所以δＷ ＝０。即向真空膨胀就一定不做体积
功。若外界不为真空，只要ｐｓｕｒｒ＞０，则就有δＷ ＝ｐｓｕｒｒｄＶ ＞０。当然，如果把这个功理解成技术功或
者轴功，则情况更复杂。即使对可逆过程
ｗｔ＝－∫ｖｄｐ＝１２Δｃ２ｆ＋ｇΔｚ＋ｗｓ
技术功不仅取决于比体积，还要取决于压力 ，轴功还要取决于宏观动能和宏观位能的变化。所以
即使对可逆过程也不一定对外做技术功或轴功。不可逆过程就更不用说了。
—６３—
（２）气体压缩时，一定消耗外功。
答：如果这个功指的是体积功，就是对的。因为气体压力一定大于零，即ｐ ＞０，气体被压缩时，必
有 ｄＶ ＜０且ｐｓｕｒｒ≥ ｐ＞０，所以无论是否可逆均有体积功 δＷ ＝ｐｓｕｒｒｄＶ ＞０。
但如果把这个功理解成技术功或者轴功，则情况更复杂。如（１）中所述，无论对可逆还是不可逆
过程，情况都更复杂，决定因素很多，不一定消耗技术功或轴功。
此外，如果把“压缩”做更宽泛的理解，比如不一定是由于“压力”而导致的“收缩”。如果“收缩”
是由于冷却导致温度下降引起，那么气体压缩时也不一定消耗外功。
（３）压力下降时，一定对外做轴功。
答：不一定。即使对于可逆的稳定流动过程，技术功包括轴功以及宏观动能和宏观位能在内，即，
ｄｐ ＜０只能保证ｗｔ＜０，轴功 ｗｓ还要取决于宏观动能和宏观位能的变化。如在喷管中，虽然 ｄｐ ＜０，
但ｗｓ＝０，压力下降是由于速度升高引起的。而且，如果压力下降是由于冷却放热温度下降引起，则
也不会对外做轴功。若对于不可逆以及非稳定流动过程，技术功的表达式将更加复杂，也不会单值地
取决于压力。
（４）压力升高时，外界一定消耗轴功。
答：不一定。原因同（３）。如在扩压管中，虽然 ｄｐ ＞０，但ｗ ｓ＝０，压力升高是由于速度下降引
起的。
（５）工质进行膨胀时，一定从外界吸热。
答：不一定。即使对于可逆的闭口系过程，δＱ ＝ｄＵ ＋ｐｄＶ，ｄＶ ＞０，δＱ的方向还取决于ｄＵ。如
果是不可逆过程则更加复杂。如向真空膨胀就不做体积功，δＷ ＝０，δＱ的方向与热力学能的变化与
ｄＵ完全一致。
（６）工质吸热时，热力学能一定增加。
答：不一定。根据热力学第一定律　δＱ ＝ｄＵ ＋δＷ ，只有当吸热量大于对外所做体积功量时，热
力学能才增加。
（７）工质从外界吸热时，一定膨胀。
答：同（５）。
（８）热力学能增加时，温度一定增加。
答：一般来说，对简单可压缩热力系Ｕ为二元函数Ｕ（Ｔ，ｐ）或Ｕ（Ｔ，ｖ），不随 Ｔ单调变化。严格
来说，只有当Ｕ是温度的单值函数Ｕ（Ｔ）时，才是这样，如对无化学反应和核反应的液体、固体和理想
气体的热力学能增加时，温度一定增加。
（９）工质吸热时，温度一定增加。
答：不一定。原因如（６）、（８）中所述。
（１０）提高液体的压力比提高气体的压力容易。
答：对。由技术功表达式 δｗｔ＝－ｖｄｐ可以看出此结论。
（１１）气体的做功能力比液体强。
答：对。同（１０）。由技术功表达式 δｗｔ＝－ｖｄｐ可以看出此结论
（１２）熵增加时，一定吸热。
—７３—
沈维道《工程热力学》考点精讲及复习思路
答：不一定。因为只有对可逆过程才有 δＱ ＝ＴｄＳ，则 ｄＳ ＞０，δＱ ＞０。所以只有对可逆过程熵
增加时才一定吸热。
讨论及结论：该例涉及的都是过程量与状态量间关系，它说明：状态量和过程量在大多数条件下
互相都不能一一对应，即状态量决定不了过程量，过程量也决定不了状态量。首先，状态参数有很多，
对于简单可压缩热力系来说，有两个独立自变量。其次，热力过程还有两个过程量。再次，过程量还
取决于热力过程的性质，如可逆、不可逆，是否准静态，等等。
秘笈：不是计算题才需要数学模型和方程，问答题、概念题同样需要用数学方程来回答，这样回答
比较精确、清晰、简练。
例２－５填空题：δｑ ＝ｄｕ ＋δｗ为一般通用形式，但在不同的工质和过程条件下有不同的简化形
式，其中 的不同形式取决于工质的性质，而 的不同形式取决于过程的性质。（北航
考研试题）
例２－６填空题：某定量气体在热力过程中ｑ ＞０，Δｕ ＞０，且ｑ ＜Δｕ，则该过程中气体 。
（北航考研试题）
　　　　　　　　　　　　　　　　　　　　　　　　　　　Ａ．放热膨胀 Ｂ．吸热膨胀 Ｃ．放热压缩 Ｄ．吸热压缩
例２－７填空题　机械能形式的热力学第一定律为 。
Ａ．δｑ ＝ｄｕ ＋δｗ　 Ｂ．δｑ ＝ｄｈ ＋δｗｔ Ｃ．δｗ ＝ｄ（ｐｖ）＋δｗｔ
（北航考研试题）
例２－８是非题　（北京科技大学考研试题）
１）膨胀功、流动功、技术功都是与过程路径有关的过程量 。（　　　　）
２）不管过程是否可逆，开口绝热稳定流动系统的技术功总等于初终态的焓差。（　　 ）
例２－９填空题　（北京理工大学考研试题）
１）若对系统加热，则参数为 必定 ；若系统对外作膨胀功，则参数为 必
定 。
２）若热力系统对外做功可用∫ｐｄｖ表示，则其过程必须在 下进行；其中可用功的数量
是 。
本章应注意的问题
１．不要认为热力学第一定律很简单，很容易掌握，真正要把它应用到实际中去，还需要下一番功
夫。特别是开口系能量方程的掌握和对焓的理解上要克服相当的困难。
２．注意学会用数学方程解决问题，更有逻辑性，更精确，更专业。特别是用微分方程表达数学模
型，更通用，更灵活。
—８３—
第三章　理想气体
本章考研要求
·掌握理想气体状态方程的各种表达形式，并应用理想气体状态方程及理想气体定值比热容进
行各种热力计算
·掌握理想气体平均比热的概念和计算方法
·掌握理想气体状态参数间的关系，包括理想气体热力学能、焓、熵的计算
·重点与难点
·变比热容的计算，热力学能、焓、熵的计算
考点一　什么是热力性质？
所有的能量转换过程都是通过热力系内部的工作物质（称为工质）进行的 。
工质的物理性质对热力过程是有影响的。
研究工质的热力性质就是热力学的重要内容之一。
热力性质实际上就是指工质的所有状态参数之间的关系。
基本状态参数 →ｐ、ｖ、Ｔ→不独立→状态方程
不可测状态参数→ｕ、ｈ、ｓ→如何用ｐ、ｖ、Ｔ表达？
热系数 →ｃｐ、ｃｖ→如何计算？
考点二　理想气体的热力性质
１．理想气体的物理模型与数学模型
微观方法→建立微观物理模型：分子不占有体积、分子之间没有相互作用力、分子与分子之间、分
子与器壁之间都是弹性碰撞→建立数学模型→ｐＶ＝ｎＲＴ、Ｒ＝ｋＮＡ＝ ＝１．３８１×１０－２３×６．０２２×１０２３＝
８．３１４　Ｊ／（ｍｏｌ
#
Ｋ）
ｐＶ＝ｎＲＴ：理想气体状态方程
Ｋ：玻耳兹曼常数
Ｎ：阿伏加德罗常数
宏观方法→建立宏观物理模型：玻意耳定律（１６６２年）、盖－吕萨克定律 （１８０２年）、查里定律
（１７８７年）→建立数学模型→对１ｋｇ气体ｐｖ＝ＲｇＴ、对ｍｋｇ气体ｐＶ＝ｍＲｇＴ、１摩尔气体ｐＶ＝ＲＴ、ｎ
摩尔气体ｐＶ＝ｎＲＴ
Ｒ＝
ｐ０Ｖｍ
Ｔ０
＝１．０１３２５×１０
５×２２．４１３８３×１０－３
２７３．１５ ＝８．３１４Ｊ／（ｍｏｌ
#
Ｋ）
无论微观方法还是宏观方法得到的理想气体状态方程是完全一致的。这主要源于理想气体模型
的简单。对于实际气体微观方法太复杂，不容易使用，即使使用也不一定准确。
实际中理想气体是不存在的。是一种假象气体。
在宏观上，把遵守理想气体状态方程的气体叫作理想气体（ＩｄｅａｌＧａｓ）或完全气体（ＰｅｒｆｅｃｔＧａｓ）。
—９３—
沈维道《工程热力学》考点精讲及复习思路
宏观条件→低压、高温、高比体积
压力足够低，比体积足够大→ｐ→０、ｖ→∞ →分子不占有体积→与微观模型一致
温度足够高 →Ｔ→∞ →分子速度大→分子势能相对就小→ 与微观模型一致
所谓的“高”或“低”都是相对的，对不同种类的工质具体要求是不一样的。
当实际气体ｐ很小，ｖ很大，Ｔ不太低时，即处于远离液态的稀薄状态时，可视为理想气体。
Ｔ ＞常温，ｐ ＜７ＭＰａ的双原子分子→理想气体
如汽车发动机和航空发动机以空气为主的燃气等。
同样条件下三原子分子（Ｈ２Ｏ，ＣＯ２）一般不能当作理想气体。
在某些条件下，如空调的湿空气，高温烟气的ＣＯ２，可以当作理想气体。
秘笈：回答某某气体是否是理想气体时，一定要注意条件，把条件阐述清楚方才完整。对所有问
题都应如此对待。
工程热力学的两大类工质
１．理想气体（ｉｄｅａｌｇａｓ）
可用简单的式子描述
如汽车发动机和航空发动机以空气为主的燃气、空调中的湿空气等。
２．实际气体（ｒｅａｌｇａｓ）
不能用简单的式子描述，真实工质
火力发电的水和水蒸气、制冷空调中制冷工质等。将在后面介绍。
３．比热容的定义
定义：　比热容
单位物量的物质升高１Ｋ或１ｏＣ所需的热量
Ｃ：质量比热容　　　 ｋＪ
ｋｇ·Ｋ　　
ｋＪ
ｋｇ·ｏＣ
ＣＭ　：摩尔比热容 　　
ｋＪ
ｋｍｏｌ·Ｋ　　
ｋＪ
ｋｍｏｌ·ｏＣ
ＣＶ　：体积比热容 　　
ｋＪ
Ｎｍ３·Ｋ
　　 ｋＪ
Ｎｍ３·ｏＣ
ＣＭ＝Ｍｃ＝２２．４１４×１０－３ＣＶ
理想气体比热容
比热容是过程量还是状态量？
—０４—
用的最多的某些特定过程的比热容：比定容热容、比定压热容
比定容热容ｃＶ
ｓｐｅｃｉｆｉｃｈｅａｔｃａｐａｃｉｔｙａｔｃｏｎｓｔａｎｔｖｏｌｕｍｅ
任意可逆过程　　　δｑ＝ｄｕ＋ｐｄｖ
ｕ是状态量，设　　　ｕ＝ｆ（Ｔ，ｖ）
ｄｕ＝（）ｄＴ＋（）ｄｖ
∴δｑ＝（）ｄＴ＋［ｐ＋（）］ｄｖ
∴δｑ＝（）ｄＴ→ｃＶ ＝（） ＝（）
物理意义：ｖ　 时１ｋｇ工质升高１Ｋ内能的增加量。
任意可逆过程　　　　 δｑ＝ｄｈ－ｖｄｐ
ｈ是状态量，设　　　 ｈ＝ｆ（Ｔ，ｐ）
ｄｈ＝（）ｄＴ＋（）ｄｐ
∴δｑ＝（）ｄＴ＋［（）－ｖ］ｄｐ
∴δｑ＝（）ｄＴ→ ｃｐ ＝（） ＝（）
物理意义：ｐ　时１ｋｇ工质升高１Ｋ焓的增加量。
３．理想气体热力学能和焓的表达式
对简单可压缩热力系，有两个独立的自变量，则
Ｕ＝Ｕ（Ｔ，Ｖ）＝Ｕ（Ｔ，ｐ）　ｕ＝Ｕｍ ＝ｕ（Ｔ，ｖ）＝ｕ（Ｔ，ｐ）
ｄｕ＝（）ｄＴ＋（）ｄｖ　
２ｕ
Ｔｖ
＝ 
２ｕ
ｖＴ
前面从微观方法论证过：对理想气体，有ｕ ＝ｆ（Ｔ）
但是，对工程来说，微观方法并不能代替宏观方法，只有宏观方法能够提供足够的、可靠的、有效
的证据。
这就是焦耳１８４３年做的气体实验。
理想气体热力学能和焓的表达式
焦耳测量气体膨胀前后水浴的温度后发现没有任何变化。
取两容器为热力系
ｗ ＝０，ｑ ＝０→%
ｕ ＝０
物理解释：体积、压力变化了热力学能却不变化，
→理想气体的热力学能与体积和压力无关。
→理想气体的热力学能只与温度有关 。ｕ＝ｆ（Ｔ）
—１４—
沈维道《工程热力学》考点精讲及复习思路
数学解释：
设ｕ＝ｆ（ｖ，Ｔ）→ｄｕ＝（ｕＴ
）
ｖ
ｄＴ＋（ｕ
ｖ
）
Ｔ
ｄｖ＝０→（ｕｖ
）
Ｔ
ｄｖ＝０→（ｕｖ
）
Ｔ
＝０
设ｕ＝ｆ（ｐ，Ｔ）→ｄｕ＝（ｕＴ
）
ｐ
ｄＴ＋（ｕ
ｐ
）
Ｔ
ｄｐ＝０→（ｕｐ
）
Ｔ
ｄｐ＝０→（ｕｐ
）
Ｔ
＝０
结论：对理想气体 →ｕ＝ｆ（Ｔ）
ｈ＝ｕ＋ｐｖ＝ｕ＋ＲｇＴ＝ｈ（Ｔ）
这是完全依赖于焦耳实验的观测结果，与理想气体的微观模型无关。再次说明了经典热力学以
宏观方法为基础，以事实为依据的特点。
ｃＶ ＝
ｄｕ
ｄＴ＝ｃＶ（Ｔ）→ｄｕ＝ｃＶｄＴ→Δｕ＝∫
２
１
ｃＶｄＴ
ｃｐ ＝
ｄｈ
ｄＴ＝ｃｐ（Ｔ）→ｄｈ＝ｃｐｄＴ→Δｈ＝∫
２
１
ｃｐｄＴ
可见理想气体热力学能和焓的计算主要取决于ｃｐ和ｃｖ的计算。
４．理想气体比热容的计算
ｈ＝ｕ＋ｐｖ＝ｕ＋ＲｇＴ
两边对温度求导可得
ｄｈ
ｄＴ＝
ｄｕ
ｄＴ＋Ｒｇ
即ｃｐ－ｃＶ ＝Ｒｇ迈尔公式 （Ｍａｙｅｒ’ｓｒｅｌａｔｉｏｎ）
Ｍｃｐ－ＭｃＶ ＝ＭＲｇ
Ｃｐｍ －ＣＶｍ ＝Ｒ适用条件→理想气体
ｃｐ－ｃＶ ＝Ｒｇ
迈尔公式的意义：
１）理想气体的ｃｐ－ｃＶ不仅与压力或比体积无关，而且也与温度无关，恒等于气体常数。但要注意
的是：ｃｐ和ｃＶ本身是与温度有关的，只是随温度同步变化；
２）只要知道ｃｐ和ｃＶ中的任一个，就可以利用迈尔公式求出另外一个，这也是实验室求比热容的方
法。由于较难测定，通常是测定ｃｐ，求取ｃＶ；
３）ｃｐ－ｃＶ表示１ｋｇ理想气体在定压下温度升高１Ｋ时对外所做的功。通常把这一点当作理想气
体的气体常数Ｒ ｇ的物理意义。
ｃＶ和ｃｐ的小结
１．ｃＶ和ｃｐ　，过程已定，可当作状态量 。
—２４—
２．对于任意气体 ｃＶ ＝（
ｕ
Ｔ
）
ｖ
、ｃｐ ＝（
ｈ
Ｔ
）
ｐ
对于理想气体 ｃＶ ＝（
ｄｕ
ｄＴ）ｖ
、ｃｐ ＝（
ｄｈ
ｄＴ）ｐ
３．迈尔（梅耶）公式：ｃｐ－ｃＶ ＝Ｒｇ
４．比热比：ｒａｔｉｏｏｆｔｈｅｓｐｅｃｉｆｉｃｈｅａｔｃａｐａｃｉｔｉｙ
γ＝
ｃｐ
ｃＶ
＝
Ｍｃｐ
ＭｃＶ
＝
ｃｐｍ
ｃＶｍ
常数？变数？
γ的微观意义
根据气体分子运动理论，分子运动的动能是按照其运动的自由度均分的（能均分定理），每一个自
由度所拥有的能量为
１
２ＲｇＴ
则ｉ个自由度的分子具有的能量为 ｉ
２ＲｇＴ
比热力学能为 ｕ＝ ｉ２ＲｇＴ
则由迈尔公式得比定压热容为 ｃｐ ＝ｃＶ＋Ｒｇ ＝
ｉ
２Ｒｇ ＋Ｒｇ ＝
ｉ＋２
２ Ｒｇ
则比热比γ＝
ｃｐ
ｃＶ
＝
ｉ＋２
２ Ｒｇ
ｉ
２Ｒｇ
＝ｉ＋２ｉ
单原子：
５
３≈１．６６７
双原子：
７
５ ＝１．４０
多原子：
９
７≈１．２９
定值比热容
若比热比为常数，则比热容也为常数。联立求解比热比定义式和迈尔公式可得
ｃＶ ＝
１
γ－１
Ｒｇ　 ｃｐ ＝
γ
γ－１
Ｒｇ
但是，分析和实验都表明，在一定温度范围内上式对单原子和双原子气体还是比较符合的，但对
三原子及多原子气体在实际中应采用实验数据，即所谓随温度变化的真实比热容或变比热容 。
定值、真实、平均比热容
定值比热容：按比热容为定值计算，称为定值比热容。
真实比热容：相应于每一温度下的比热容值称为气体的真实比热容。
ｃｐ ＝（ａ＋ｂＴ＋ｃＴ
２＋ｄＴ３＋····）Ｒｇ
ｃｐ ＝ａ０＋ａ１Ｔ＋ａ２Ｔ
２＋ａ３Ｔ
３
平均比热容
—３４—
沈维道《工程热力学》考点精讲及复习思路
理想气体热力学能和焓的计算
１）按定比热容计算
Δｕ＝∫
２
１
ｃＶｄＴ＝ｃＶ（Ｔ２－Ｔ１）　Δｈ＝∫
２
１
ｃｐｄＴ＝ｃｐ（Ｔ２－Ｔ１）
２）按真实比热容或者说变比热容计算
Δｈ＝∫
２
１
ｃｐｄＴ＝∫
２
１
（ａ＋ｂＴ＋ｃＴ２＋ｄＴ３＋····）ＲｇｄＴ
Δｕ＝∫
２
１
ｃＶｄＴ＝∫
２
１
（ａ－１＋ｂＴ＋ｃＴ２＋ｄＴ３＋····）ＲｇｄＴ
３）按平均比热容计算
Δｈ１２ ＝∫
２
１
ｃｐｄＴ＝∫
ｔ２
ｔ１
ｃｐｄｔ＝∫
ｔ２
ｔ０
ｃｐｄｔ－∫
ｔ１
ｔ０
ｃｐｄｔ＝ｃｐ
ｔ２
ｔ０
（ｔ２－ｔ０）－ｃｐ
ｔ１
ｔ０
（ｔ１－ｔ０）
若ｔ０＝０℃，则上式可写为Δｈ１２ ＝ｃｐ ｔ２
ｔ０
ｔ２－ｃｐ
ｔ１
ｔ０
ｔ１
同理可得Δｕ１２ ＝ｃＶ
ｔ２
ｔ０
ｔ２－ｃＶ
ｔ１
ｔ０
ｔ１
迈尔公式对平均比热容也是成立的，即有ｃｐ
ｔ
０－ｃＶ
ｔ
０ ＝Ｒｇ
４）按焓温表计算
Δｈ＝ｈ２（Ｔ２）－ｈ１（Ｔ１）
附表中列出了空气和其他理想气体的焓和热力学能随温度的变化。
注意：焓和热力学能零点的选择问题。
秘笈：比热容计算的目的不是比热容本身，也不是为了计算热量，而是为了计算热力学能和焓，以
及后面的熵。
５．理想气体熵的计算
—４４—
对理想气体代入焓表达式和状态方程得ｄｓ＝ｄｈ－ｖｄｐＴ ＝ｃｐ
ｄＴ
Ｔ－Ｒｇ
ｄｐ
ｐ
则熵增为Δｓ１２ ＝ｓ２－ｓ１ ＝∫
Ｔ２
Ｔ１
ｃｐ
ｄＴ
Ｔ－Ｒｇ∫
ｖ２
ｖ１
ｄｐ
ｐ＝∫
Ｔ２
Ｔ１
ｃｐ
ｄＴ
Ｔ－Ｒｇｌｎ
ｐ２
ｐ１
若按定比热容计算，则有
Δｓ１２ ＝ｃｐ∫
Ｔ２
Ｔ１
ｄＴ
Ｔ－Ｒｇ∫
ｖ２
ｖ１
ｄｐ
ｐ＝ｃｐｌｎ
Ｔ２
Ｔ１
－Ｒｇｌｎ
ｐ２
ｐ１
同理可得Δｓ１２ ＝ｓ２－ｓ１ ＝ｃＶｌｎ
Ｔ２
Ｔ１
＋Ｒｇｌｎ
ｖ２
ｖ１
Δｓ１２ ＝ｓ２－ｓ１ ＝ｃＶｌｎ
ｐ２
ｐ１
＋ｃｐｌｎ
ｖ２
ｖ１
若按变比热容计算，则有
Δｓ１２ ＝∫
Ｔ２
Ｔ０
ｃｐ
ｄＴ
Ｔ－∫
Ｔ１
Ｔ０
ｃｐ
ｄＴ
Ｔ－Ｒｇｌｎ
ｐ２
ｐ１
＝ｓ０Ｔ２－ｓ
０
Ｔ１－Ｒｇｌｎ
ｐ２
ｐ１
式中，ｓ０Ｔ ＝∫
Ｔ
Ｔ０
ｃｐ
ｄＴ
Ｔ定熵函数
显然，只要做出ｓ０Ｔ ～Ｔ表，就可以查表求出熵增。
附表中给出了空气及其他理想气体在不同温度下的值。
这里仍存在一个熵值零点问题。
熵值零点问题
一般来说，热力学中关心的是熵的变化量，并不关心其绝对值是多少。零点Ｔ０可以任意选择。
但若考虑不同工质的熵增必须有一个共同的起点，就只能选择绝对零度作为熵的零点，Ｔ０＝０Ｋ。
这样计算出来的熵称为绝对熵。
例３－１　热力学第一定律表达式可写作 δｑ ＝ｄＵ ＋ｐｄＶ，δｑ ＝ｃｖｄＴ ＋ｐｄＶ，δｑ ＝ｃｖｄＴ ＋ｄ
（ｐＶ），三者有何不同？　
答：三者的适用范围不同，如下所示。
δｑ＝ｄＵ＋ｐｄＶ，第一表达式，适用于平衡态，可逆过程，一般用于简单可压缩闭口系
δｑ＝ｃｖｄＴ＋ｐｄＶ，在上面基础上增加理想气体的条件。
δｑ＝ｃｖｄＴ＋ｄ（ｐＶ）在上面基础上增加定压过程的条件。
秘笈：从方程和公式最原始的形式出发，推导过程中加入了什么条件，该方程和公式就适用于什
么条件。
例３－２问答题：“由于理想气体的焓、热力学能仅为温度的单值函数，因此，如果在给定的两温度
Ｔ１，Ｔ２，间发生状态变化时，对任何理想气体的ｈ，ｕ的变化值都相同”，这种推断对吗？。（北京科技
大学考研试题）
答：任何理想气体　　ｄｈ ＝ｃｐｄＴ，ｄｕ ＝ｃｖｄＴ、ｃｐ，ｃｖ不同，所以ｈ，ｕ变化值不同。
例３－３是非题：（北京科技大学考研试题）
—５４—
沈维道《工程热力学》考点精讲及复习思路
２）水在定温汽化成水蒸气过程中温度保持不变（ΔＴ ＝０），其热力学能Δｕ也不变。（　　　）
秘笈：密切注意公式使用条件，通常结论是随条件变化的。
例３－４　如图所示为自输气总管向汽缸充气。设输气总管中空气的压力为 ０．６ＭＰａ，温度为
２７℃，而弹簧变形正比于压缩力，忽略汽缸散热，汽缸内空气的起始体积是Ｖ０，大气压力为ｐｂ，活塞面
积为Ａ，弹簧的弹性系数为ｋ，弹簧位移为ｘ。试求充气过程中汽缸内空气的温度与ｐｂ，Ｖ０，Ａ，ｘ，ｋ
的关系，分析在何种情况下是一个常数，并求其值是多少？
解：１．物理模型：取汽缸内空间为热力系
，这是一个非稳态流动开口系（Ｃ．Ｖ．），不向外界散热，并通过活塞、弹簧、充气口与外界交换功，
通过充气带入质量及能量。这些量的多少决定了汽缸内空气的温度。
解：２．数学模型：
由一般瞬态能量方程得
０＝（ｍ２ｕ２－ｍ０ｕ０）＋０（ｈ
－（ｍ２－ｍ０）（ｈ＋∫
Ｖ２
Ｖ０
（
ｋｘ
Ａ＋ｐｂ）ｄＶ①
理想气体物性方程
ｍ０ ＝
ｐｂＶ０
ＲｇＴ０
②　　　　ｍ２ ＝
（
ｋｘ
Ａ＋ｐｂ）Ｖ２
ＲｇＴ２
③
ｕ２ ＝ｃＶＴ２④　　　　　ｕ０ ＝ｃＶＴ０⑤
ｈ＝ｃｐＴ０⑥　　　　　
其他方程Ｖ２－Ｖ０ ＝Ａｘ⑦
上述７个方程，共９个未知数，忽略宏观动能和位能２个未知数，方程组封闭。
３．求解数学模型：
忽略宏观动能和位能，将② ～⑦代入①并整理得
—６４—
０＝ｃＶ［
（
ｋｘ
Ａ＋ｐｂ）Ｖ２
ＲｇＴ２
Ｔ２－
ｐｂＶ０
ＲｇＴ０
Ｔ０］－［
（
ｋｘ
Ａ＋ｐｂ）Ｖ２
ＲｇＴ２
－
ｐｂＶ０
ＲｇＴ０
］ｃｐＴ０＋［
ｋｘ２
２ ＋ｐｂ（Ｖ２－Ｖ０）］
可解得
Ｔ２ ＝
γＴ０（
ｋｘ
Ａ＋ｐｂ）（Ｖ０＋Ａｘ）
ｋｘ
Ａ（Ｖ０＋
γ＋１
２ Ａｘ）＋γｐｂ（Ｖ０＋Ａｘ）
显然，Ｔ２是ｐｂ，Ｖ０，Ａ，ｘ，ｋ的函数，即Ｔ２会在活塞移动中变化。
４．讨论与结论
Ｔ２ ＝
γＴ０（
ｋｘ
Ａ＋ｐｂ）（Ｖ０＋Ａｘ）
ｋｘ
Ａ（Ｖ０＋
γ＋１
２ Ａｘ）＋γｐｂ（Ｖ０＋Ａｘ）
（１）只有当　ｐｂ＜＜ｋｘ／Ａ，Ｖ０＜＜Ａｘ，即Ｖ０＋Ａｘ≈Ａｘ，Ｖ０＋（γ＋１）Ａｘ／２≈ （γ＋１）Ａｘ／２，
ｋｘ／Ａ ＋ｐｂ≈ｋｘ／Ａ时，有
Ｔ２≈
γＴ０
ｋｘ
ＡＡｘ
ｋｘ
Ａ
γ＋１
２ Ａｘ＋γｐｂＡｘ
≈
２γＴ０
γ＋１
Ｔ２≈
２γＴ０
γ＋１
＝
２×１．４０Ｔ０
１．４０＋１ ＝１．１７Ｔ０ ＝３５０Ｋ＝７７℃
Ｔ２ ＝
γＴ０（
ｋｘ
Ａ＋ｐｂ）（Ｖ０＋Ａｘ）
ｋｘ
Ａ（Ｖ０＋
γ＋１
２ Ａｘ）＋γｐｂ（Ｖ０＋Ａｘ）
（２）只有当　ｐｂ＞＞ｋｘ／Ａ，Ｖ０＞＞Ａｘ，即Ｖ０＋Ａｘ≈Ｖ０，Ｖ０＋（γ＋１）Ａｘ／２≈Ｖ０，ｋｘ／Ａ ＋
ｐｂ≈ｐｂ，ｋｘ／Ａ ＋γｐｂ≈γｐｂ时，有
Ｔ２≈
γＴ０（
ｋｘ
Ａ＋ｐｂ）Ｖ０
ｋｘ
ＡＶ０＋γｐｂＶ０
≈
γＴ０ｐｂ
γｐｂ
＝Ｔ０ ＝３００Ｋ＝２７℃
结论：只有在两种极限情况下温度是常数，一般情况下汽缸内空气的温度与ｐｂ，Ｖ ０，Ａ，ｘ，ｋ的
相关。
秘笈：学会这种按部就班的解题方式，以不变应万变。其关键是物理模型的建立及机理分析。
例３－５　理想气体由初态１经任意压缩过程变化至终态２，试
在ｐ－ｖ图上用面积表示其比焓Δｈ的大小。（重庆大学考研试题）
解：在ｐ－ｖ图上画出１－２过程。
热一定律　　ｑ ＝Δｈ ＋ｗｔ
绝热过程　　Δｈ ＝－ｗｔ
理想气体定温过程　　Δｈ ＝０
同理可在ｐ－ｖ图上表示　Δｕ（南航考研试题）
—７４—
沈维道《工程热力学》考点精讲及复习思路
秘笈：学会利用热一定律及特殊过程（如绝热、定温等）在ｐ－ｖ图上表示内能和焓，热，在Ｔ－ｓ图
上表示各种功。
例３－６　已知某理想气体的比热容为定值，当其由初态（ｐ１，Ｔ１）经历任意过程而达到终态（ｐ２，
Ｔ２），试证明任何过程总是满足关系Ｔ２＝Ｔ１ｅ
（ｓ２－ｓ１）／ｃｖ（ｖ１／ｖ２）
（ｋ－１）。（北京理工大学考研试题）
解：任何过程都必须满足热一定律和理想气体定比热容关系式。
理想气体任意过程（三参数关系，不是过程方程）
热一定律δｑ ＝ｄｕ ＋δｗ→Ｔｄｓ＝ｃｖｄＴ ＋ｐｄｖ→
ｄｓ
ｃｖ
＝ｄＴＴ＋
ｐｄｖ
ｃｖＴ
→ ｄｓｃｖ
＝ｄＴＴ＋
Ｒｇｄｖ
ｃｖ
→ ｄｓｃｖ
＝ｄＴＴ＋（κ
－１）ｄｖｖ→Ｔ２ ＝Ｔ１ｅ
（ｓ２－ｓ１）／ｃｖ（ｖ１／ｖ２）
（κ－１）
秘笈：学会从最原始的方程出发进行推导。
本章应注意的问题
１．注意工质的热力性质不仅仅是状态方程，热力学能、焓、熵、比热容的计算也是非常重要的内
容，要注意掌握。因此，要把工质的热力性质理解为一组描写三个参数之间关系的数学方程。
２．考虑比热容随温度变化后，产生了多种计算理想气体热力参数变化量的方法，要熟练地掌握和
运用这些方法，必须多加练习才能达到目的。
—８４—
循环的方法求解。
２．数学模型及求解：
ｗ０ ＝∮ｐｄｖ＝０．５（ｐ２－ｐ１）（ｖ３－ｖ１）
ｑ１ ＝ｃｖ（Ｔ２－Ｔ１）＋ｃｐ（Ｔ３－Ｔ２）
　 ＝ｃｖＴ１［（
Ｔ２
Ｔ１
－１）＋κ
Ｔ２
Ｔ１
（
Ｔ３
Ｔ２
－１）］
　 ＝
ＲｇＴ１
κ－１
［（
ｐ２
ｐ１
－１）＋κ
ｐ２
ｐ１
（
ｖ３
ｖ２
－１）］
　 ＝
ｐ１ｖ１
κ－１
［（
ｐ２
ｐ１
－１）＋κ
ｐ２
ｐ１
（
ｖ３
ｖ２
－１）］
ηｔ＝
ｗ０
ｑ１
＝
０．５（ｐ２－ｐ１）（ｖ３－ｖ１）
ｐ１ｖ１
κ－１
［（
ｐ２
ｐ１
－１）＋κ
ｐ２
ｐ１
（
ｖ３
ｖ２
－１）］
＝
（κ－１）（ｐ２－ｐ１）（ｖ３－ｖ１）ｖ２
２ｖ１［（ｐ２－ｐ１）＋κｐ２（ｖ３－ｖ１）］
＝
（κ－１）（ｖ３－ｖ１）ｖ２
２ｖ１（１＋κｐ２
ｖ３－ｖ２
ｐ２－ｐ１
）
４．讨论及结论：
循环热效率与各转折点参数有关，不管参数是温度还是压力、比体积，亦或是焓、内能和熵。
秘笈：循环变，方法不变。以不变应万变。
例１０－７作图题：在Ｔ －ｓ图上示出（ａ）、（ｂ）和（ｃ）三个热力循环，试从热力学第二定律简要分析
哪个循环的热效率最高，哪个最低。（北航２００２年考研试题）
解：根据卡诺定理，谁的平均吸热温度高，平均放热温度低，谁的热效率高。据此判断：热效率（ｃ）
最高，（ｂ）最低。
但是，就循环功而言，（ｃ）最低，（ｂ）较高，（ａ）最高。
四、提高燃气轮机循环热效率的措施
上述改变循环参数τ、π、ηＣ和ηＴ的方法只是在既定的循环下通过有限的“量变”来达到提高燃
气轮机循环热效率和循环功的目的。应该说是一种 “拼体力”的方法。
更聪明的办法是：针对循环的固有缺陷进行改进，使循环接近卡诺循环，这才是改进循环、提高循
环性能、使循环发生“质变”的根本途径。
—０９１—
燃气轮机的复杂性与变通性为改进留下了巨大的空间。
１．回热（Ｒｅｇｅｎｅｒａｔｉｏｎ）
就是利用燃气轮机出口废气温度Ｔ４加热燃烧室前的高压空气，工质内部自己加热自己，故称回热
（Ｒｅｇｅｎｅｒａｔｉｏｎ）。
如用温度法来分析，回热后，加热过程由２－３改为６－３，平均吸热温度提高，同时，放热过程由４
－１改为５－１，平均放热温度下降，故热效率提高。这是热力学第二定律对回热提高热效率的解释，
它比热力学第一定律（热量法）的解释更真实地反映了回热的本质。
如增压比π提高使Ｔ２′＝Ｔ４，则循环１２′３′４１就不可能采用回热。
可采用回热的最大增压比为πｍａｘ＝τ
κ
２（κ－１） ＝ （
Ｔ３
Ｔ１
）
κ
κ－
槡
１
＝πｏｐｔ
又一个温比决定压比的例子。温度还是最终的决定因素。
上述回热要达到Ｔ５＝Ｔ２，Ｔ６＝Ｔ４，即一直加热到冷、热流体间温差为零，理论上需要回热器换热
面积无穷大，是一种极限的理想状况，称为理想回热，是不可能实现的。
实际中回热器的换热面积是有限的，只能把２点工质加热到６′点，Ｔ５′＞Ｔ２，Ｔ６′＜Ｔ４，这时的回
热称为实际回热。
实际回热中利用的热量与可利用热量（即理想回热量）之比称为回热度，用σ表示，即
σ＝
ｈ６＇－ｈ２
ｈ４－ｈ２
＝
ｈ４－ｈ５＇
ｈ４－ｈ２
→σ＝
Ｔ６＇－Ｔ２
Ｔ４－Ｔ２
＝
Ｔ４－Ｔ５＇
Ｔ４－Ｔ２
实际回热总有σ＜１。选择的回热度不能太大，也不能太小。太大不可逆损失小，热效率增加大，
但需要回热器大，投资大，资金回收慢；太小则不可逆损失大，热效率增加少，节能效果不显著，资金同
样回收确定。目前实际使用中的回热度很少有高于０．８５的。
采用回热后，从外部热源的吸热量为
ｑ１ ＝ｈ３－ｈ６＇
＝ｈ３－［ｈ２＋σ（ｈ４－ｈ２）］
—１９１—
沈维道《工程热力学》考点精讲及复习思路
＝ｃｐ［（Ｔ３－Ｔ２）－σ（Ｔ４－Ｔ２）］
向外部冷源的放热量为
ｑ２ ＝ｈ５＇－ｈ１ ＝［ｈ４－σ（ｈ４－ｈ２）］－ｈ１
＝ｃｐ［（Ｔ４－Ｔ１）－σ（Ｔ４－Ｔ２）］
则回热循环的热效率为
ηｔ，ＲＧ ＝１－
ｑ２
ｑ１
＝１－
ｃｐ［（Ｔ４－Ｔ１）－σ（Ｔ４－Ｔ２）］
ｃｐ［（Ｔ３－Ｔ２）－σ（Ｔ４－Ｔ２）］
ηｔ，ＲＧ ＝１－
（Ｔ４－Ｔ１）－σ（Ｔ４－Ｔ２）
（Ｔ３－Ｔ２）－σ（Ｔ４－Ｔ２）
＝
（Ｔ３－Ｔ２）－（Ｔ４－Ｔ１）
（Ｔ３－Ｔ２）－σ（Ｔ４－Ｔ２）
＝
（
Ｔ４
Ｔ３
Ｔ３
Ｔ１
－１）
（
Ｔ４
Ｔ３
Ｔ３
Ｔ１
－１）－σ（
Ｔ４
Ｔ３
Ｔ３
Ｔ１
Ｔ１
Ｔ２
－１）
（１－
Ｔ１
Ｔ２
）
则回热循环的热效率决定于循环各转折点温度，循环热效率的本质仍然是温度。
ηｔ，ＲＧ ＝
τ
π
κ－１
κ
－１
（
τ
π
κ－１
κ
－１）－σ（ τ
π
２（κ－１）
κ
－１）
（１－ １
π
κ－１
κ
）
＝ １
１－σ τ－π
２（κ－１）
κ
τπ
κ－１
κ －π
２（κ－１）
κ
（１－ １
π
κ－１
κ
）
可以证明：
０＜１－σ τ－π
２（κ－１）
κ
τπ
κ－１
κ －π
２（κ－１）
κ
＜１必有ηｔ，ＲＧ ＞（１－
１
π
κ－１
κ
）
回热必使循环热效率提高。可见，采用公式法分析的结果与前面采用热量法和温度法进行的定
性分析结果是完全一致的。
从图中可以看出如下规律：
１）只有当π ＜πｍａｘ时回热循环热效率ηｔ，ＲＧ＞ηｔ，说明只有这时才能采用回热，且回热度越高η
ｔ，ＲＧ越高。
—２９１—
２）在相同的温度极限范围内（τ相同），回热循环的热效率随增压比增大也经历一个先升后降的
过程，因此也存在一个使热效率最大的最佳增压比πｏｐｔ，且πｏｐｔ随回热度σ增大而减小。
３）虽然温比τ对燃气轮机理想循环热效率没有影响，但对带回热的燃气轮机理想循环热效率影
响很大 。
４）τ增大还使得可进行回热的π的范围增大，表现在最佳增压比πｏｐｔ及πｍａｘ都随τ的增大而增大。
温比对回热循环特别重要。
２．回热＋分级压缩、中间冷却＋再热
压气机采用分级压缩的方法来减少压气机的耗功，在燃气轮机循环中若采用此法可以增大循
环功。
在这里热量法和温度法都失灵了！
压气机采用两级压缩，中间冷却的燃气轮机循环１－ａ－ｂ－２Ｔ－３－４－１，与原循环１－２－３－４
－１相比，热效率是升还是降？
循环分解法：将循环１ａｂ２Ｔ３４１分解为１２３４１和ａｂ２Ｔ２ａ。
∵ηｔ１２３４１＞ηｔａｂ２Ｔ２ａ　　　　　　∴ηｔ１ａｂ２Ｔ３４１＞ηｔ１２３４１
即采用分级压缩、中间冷却后循环热效率不升反降！
如果采用分级压缩、中间冷却的同时还采取回热措施，效果就不同了。
—３９１—
沈维道《工程热力学》考点精讲及复习思路
与仅采用回热措施的循环１２６３４５１相比，从外部热源的吸热过程未变，仍为６－３，向外部冷源的
放热过程则由５－１改为７－１和ａ－ｂ，则在吸热量未变的情况下，由于循环功增加，热效率增加（热量
法）；或者说在平均吸热温度未变的情况下，由于平均放热温度下降，热效率增加（温度法）。
造成这一现象的根本原因在于：分级压缩、中间冷却的作用加大了循环的回热范围！
按照上述原理，如果能提高Ｔ４，则也可以在高温段扩大回热的温度范围，从而提高热效率。这就
是采用再热（Ｒｅｈｅａｔ）的方法。　
分级压缩、中间冷却和再热都将循环回热范围扩大，前者降低了与低温热源的温差，后者降低了
与高温热源的温差。增强了回热效果，减小了传热的不可逆性，使热效率增加。
回热、分级压缩、中间冷却、再热循环系统图 。
理论上甚至可以采用无穷多级涡轮再热，同时采用无穷多级压气机间冷，使膨胀趋近于等温膨
胀，压缩趋近于等温压缩，而等压加热和等压放热全部用回热进行。这样，循环只在定温过程中与外
部热源和冷源接触，完全消除了温差传热的不可逆因素，这一循环称为艾利克逊循环（Ｅｒｉｃｓｓｏｎｃｙ
ｃｌｅ）。热效率就等于两定温热源间进行的卡诺循环的热效率。
艾利克逊循环由艾利克逊（ＪｏｈｎＥｒｉｃｓｓｏｎ，１８０３－１８８９）在１８３３年取得专利权，比布莱顿循环还
要早。
艾利克逊循环并不能在实际中应用，但它利用回热来弥补气体动力循环的不足之处，消除不可逆
性，从而提高热效率的思想却很有启示作用。前述的回热与分级压缩、中间冷却和再热相结合的燃气
轮机系统正是艾利克逊循环在工程实际中的体现。
—４９１—
实际上，不只是艾利克逊循环，当用任意一个多变过程去代替艾利克逊循环中的两个定压回热过
程时，形成的这一类循环统称为概括性卡诺循环，其热效率都等于卡诺循环的热效率。
另一个著名的概括性卡诺循环的特例是当ｎ ＝∞（即采用定容回热）时的循环，称为斯特林循环，
与艾利克逊循环不同的是斯特林循环已经有了实际应用。
斯特林循环是可以在实际中实现的概括性卡诺循环。
其热效率为
ηｔ＝１－
ｑ２
ｑ１
＝１－
Ｔ１（ｓ１－ｓ２）
Ｔ３（ｓ４－ｓ３）
ｓ２－ｓ１ ＝Ｒｇｌｎ
ｖ２
ｖ１
＝Ｒｇｌｎ
ｖ３
ｖ４
＝ｓ３－ｓ４则ηｔ＝１－
Ｔ１
Ｔ３
考点四：斯特林循环
１－２：定温压缩过程，图（ａ）。配气活塞２在上死点不动，动力活塞１由其下死点移至上死点，在
两个活塞之间的气体受到压缩而压力升高，同时由于压缩腔的气缸壁有冷却水冷却，而压缩过程也进
行得比较缓慢，冷却比较充分，因而可近似认为是定温压缩过程。
２－３：定容预热过程，图（ｂ）。动力活塞１在上死点不动，配气活塞２向下移动，迫使压缩腔内气
体经气缸外连通管流入配气活塞上方的膨胀腔。在过程中气体体积不变，在流经蓄热式回热器３时
吸收了回热器所蓄的热能而使温度升高。
３－４：定温膨胀过程，图（ｃ）。外部燃烧系统通过气缸顶部向膨胀腔内气体加热，气体同时膨胀
推动配气活塞２和动力活塞１一起向下移动，输出体积功，且吸热量和功量相等，气体温度保持不变。
—５９１—
沈维道《工程热力学》考点精讲及复习思路
４－１：定容回热过程，图（ｄ）。这时动力活塞１在下死点不动，配气活塞２向上移动，迫使膨胀腔
内气体经气缸外连通管流入两活塞间的气缸压缩腔。该过程中气体的体积不改变，在流经蓄热式回
热器３时向回热器放热，温度下降，回热器３由于蓄积热能而温度升高。
斯特林发动机工作过程
斯特林发动机工作过程
ＲｏｂｅｒｔＳｔｉｒｌｉｎｇ，１７９０—１８７８
如瑞典于１９９６年７月正式服役的世界上第一艘装备“不依赖空气推进装置（ＡＩＰ）”的潜艇“哥特
兰”号就使用了两台功率各为７５ｋＷ的Ｖ４－２７５Ｒ斯特林发动机。它能用大约６ｋｎ的航速在水下连续
航行１５天不换气，燃用液氧和柴油。
瑞典潜艇“哥特兰”号正进行反航母演练
—６９１—
瑞典潜艇 “哥特兰”号的Ｖ４－２７５Ｒ斯特林发动机
日本“苍龙”号推进系统包括２台柴油机、４台瑞典考库姆公司的Ｖ４—２７５ＲＭｋⅢ型斯特林发动机
和１台主推进电动机。水面最高航速为１２节，水下２０节。其水下续航力比亲潮级有了大幅度改进
和提高。“苍龙”号将于２００９年３月完成所有设备安装及调试工作，正式入役。
目前，日本海上自卫队共拥有１６艘潜艇，其中新型“亲潮”级潜艇６艘、“春潮”级７艘和“夕潮”
级３艘。日本计划以每年更换一艘潜艇的速度，将所有的“夕潮”级潜艇及“亲潮”级潜艇全部换装为
加装ＡＩＰ系统的新型“亲潮”级潜艇。
典型例题
例１０－８作图题：定性地画出具有回热的燃气轮机装置示意图，并在Ｔ －ｓ图上定性地分析回热
对热效率的影响。（北航２００４年考研试题）
答：温度法：回热使平均吸热温度提高，同时，放热平均放热温度下降，与热源温差减小，不可逆性
减小，故热效率提高。存在使回热不能进行的最大增压比。
例１０－９计算题：某燃气轮机装置循环为Ｂｒａｙｔｏｎ循环，即定压加热循环，压气机出口压力表读数
为０．５５ＭＰａ，进口为环境大气压ｐ１＝０．１ＭＰａ，环境温度ｔ２＝２７℃。燃气轮机涡轮进口温度Ｔ３＝
１０００Ｋ。取空气的ｃｐ＝１００４Ｊ／（ｋｇ·Ｋ），κ＝１．４，试求：
（１）循环热效率；
（２）循环的最佳增压比；
—７９１—
沈维道《工程热力学》考点精讲及复习思路
（３）最佳增压比下的循环净功和热效率。（北航２００７年考研试题）
解：１．物理模型：该燃气轮机理想循环中每一转折点均确定，因此该循环确定，可按照分析循环的
方法求解。
２．数学模型及求解：
ηｔ＝１－
ｑ２
ｑ１
＝１－
ｃｐ（Ｔ４－Ｔ１）
ｃｐ（Ｔ３－Ｔ２）
＝１－
Ｔ４－Ｔ１
Ｔ３－Ｔ２
Ｔ２ ＝Ｔ１（
）κ－１
κ
＝３００×５．５
１．４－１
１．４
＝４８８．３Ｋ＝２１５．３°Ｃ
Ｔ４ ＝Ｔ３（
）κ－１
κ
＝１０００×１．４－１１．４
＝
６１４．４Ｋ＝３４１．４℃
ηｔ＝１－
Ｔ４－Ｔ１
Ｔ３－Ｔ２
＝１－３４１．４－２７７２７－２１５．３＝３８．５６％
ｗ０ ＝ｗｔ２３＋ｗｔ１２ ＝ｗＴ－ ｗＣ
＝
κＲｇＴ３
κ－１
［１－（）κ－１
κ
］－
κＲｇＴ１
κ－１
［（）
κ－１
κ
－１］
＝
κＲｇＴ１
κ－１
［τ（１－ １
π
κ－１
κ
）－（π
κ－１
κ －１）］
＝
κＲｇＴ１
κ－１
［τ＋１－（τ
π
κ－１
κ
＋π
κ－１
κ）］　 τ
π
κ－１
κ
·π
κ－１
κ ＝τ＝常数
当
τ
π
κ－１
κ
＝π
κ－１
κ 时，循环功ｗ０最大。
可得最佳增压比πｏｐｔ
πｏｐｔ＝τ
κ
２（κ－１）
＝ τ
κ
κ－槡 １ ＝ （
Ｔ３
Ｔ１
）
κ
κ－
槡
１
＝ （
１０００
３００）
１．４
１．４－
槡
１
＝８．２２３
最佳增压比下的循环净功
ｗ０ｍａｘ＝
κＲｇＴ３
κ－１
［１－（）κ－１
κ
］－
κＲｇＴ１
κ－１
［（）
κ－１
κ
－１］
—８９１—
＝１．４×０．２８７１．４－１ ×［１０００×（１－ １
８．２２３
１．４－１
１．４
）－３００×（８．２２３
１．４－１
１．４ －１）］
＝２０５．５ｋＪ／ｋｇ
Ｔ２ ＝Ｔ１（
）κ－１
κ
＝３００×８．２２３
１．４－１
１．４
＝５４７．７·Ｋ＝２７４．７℃
Ｔ４ ＝Ｔ３（
）κ－１
κ
＝１０００× １
８．２２３
１．４－１
１．４
＝５４７．７Ｋ＝２７４．７℃
ηｔ＝１－
Ｔ４－Ｔ１
Ｔ３－Ｔ２
＝１－２７４．７－２７７２７－２７４．７
＝４５．２４％
４．讨论及结论：Ｔ４＝Ｔ２时循环功最大。
考点五：空气喷气发动机循环
一、涡轮喷气发动机的理想循环
涡轮喷气发动机结构与工作过程
　　　
涡轮喷气发动机循环图示
涡轮喷气发动机循环功为
ｗ０ ＝ｗｔ３５＋ｗｔ０２
＝ｗｔ３５－ ｗｔ０２
＝（ｈ３－ｈ５）－（ｈ２－ｈ０）
＝（ｈ３－ｈ４＋ｈ４－ｈ５）－（ｈ２－ｈ１＋ｈ１－ｈ０）
＝ｗＴ－ ｗＣ ＋（ｈ４－ｈ５）－（ｈ１－ｈ０）
＝ １２（ｃ
２
ｆ５－ｃ
２
ｆ４）－
１
２（ｃ
２
ｆ０－ｃ
２
ｆ１）
若忽略压气机、燃烧室和涡轮进出口气体速度的变化，即认为在发动机内部各截面速度基本相等，
—９９１—
沈维道《工程热力学》考点精讲及复习思路
二、提高涡轮喷气发动机循环功的方法
１．复燃加力的方法
由于只再热，不回热，热效率肯定会下降。
由于尾喷管中没有像涡轮那样复杂而又旋转的零件，因而Ｔ４′＞Ｔ３，但热效率仍然会下降。Ｔ４′的
提高主要是用来尽可能地增大循环功。
涡轮喷气发动机能够采用复燃加力方法的关键是这种方法不需要增加很多的设备，发动机重量
增加不多却能使推力增加很大，大大增加了发动机的推重比，收益明显。
带加力燃烧室的美国Ｆ１１９航空发动机 。
２．喷射液体的方法
在压气机进口喷射容易蒸发的液体（水、酒精或两者的混合液），利用液体的汽化焓（潜热）降温。
能够减少压气机消耗的功，也可以间接增大燃气轮机循环功。
英国鹞式垂直起落战斗机
三、提高涡轮喷气发动机推进效率的方法
并不是所有的循环功都能用于推动飞机前进，由功的定义可知只有飞机受到的推力与飞机的速
度之积才是飞机所获得的功率。
—００２—
ｗＰ ＝ｆｃｆ０ ＝（ｃｆ５－ｃｆ０）ｃｆ０
把飞机得到的推动功与发动机输出的循环功之比称为推进效率 。
ηＰ ＝
ｗＰ
ｗ０
＝
（ｃｆ５－ｃｆ０）ｃｆ０
１
２（ｃ
２
ｆ５－ｃ
２
ｆ０）
＝
２ｃｆ０
ｃｆ５＋ｃｆ０
＝ ２
ｃｆ５／ｃｆ０＋１
ηＰ ＝
２
ｃｆ５／ｃｆ０＋１
由上式可知，喷气发动机的推进效率ηｐ与发动机的喷射速度与飞机飞行速度之比ｃｆ５／ｃｆ０有关 ，ｃ
ｆ５／ｃｆ０越大，ηｐ就越小，由于ｃｆ５／ｃｆ０＞１，所以必有ηｐ＜１。只有当ｃｆ５／ｃｆ０＝１时，ηｐ＝１，为最大值，但
由公式知此时循环功ｗ０＝０，推力为零，故没有实际意义。
实际应用中，会呈现以下两种现象：
第一，飞机飞行速度越大，喷气发动机推进效率就越高，再加上冲压效应增强，循环热效率提高，
因此喷气式发动机特别适合于高速飞行，随飞行速度的加大，飞机得到的有效功加大，恰好满足了高
速飞行阻力急剧增加的需要。
第二，对低速飞行，喷气推进效率下降，故喷气推进不适合于低速飞行。要提高喷气推进的效率，
就要降低发动机排气速度ｃｆ５，循环功就要下降。为保持发动机的功率，就需要提高空气流量。
对低速飞行需要采用大流量、低排速的方法来提高推进效率。
涡轮风扇发动机
通常把流过外涵道和内涵道的空气流量之比称为涵道比 。
飞机的飞行速度ｃｆ０越低，发动机排气速度ｃｆ５越大，需要的涵道比就越大。因此一般做超声速飞
行的军用机采用较小的涵道比，民航机、运输机采用较大的涵道比。
喷气式发动机的总效率为
ηｔｏｔ＝
飞机得到的推动功
燃料放出的热量
＝
ｗＰ
ｑ１
＝
ｗ０
ｑ１
ｗＰ
ｗ０
＝ηｔηＰ
涡轮风扇发动机
涡轮风扇发动机由于排气速度降低，降低了噪声。外涵空气的混入也使发动机排气
—１０２—
沈维道《工程热力学》考点精讲及复习思路
四、冲压式喷气发动机的理想循环
冲压式喷气发动机
冲压比为π＝
ｐ２
ｐ０
＝［
１＋（κ－１）２ Ｍａ２０
１＋（κ－１）２ Ｍａ２２
］
κ
κ－１
循环热效率为ηｔ＝１－
１
π
κ－１
κ
＝１－
１＋（κ－１）２ Ｍａ２２
１＋（κ－１）２ Ｍａ２０
＝
（κ－１）（Ｍａ２０－Ｍａ
２
２）
２＋（κ－１）Ｍａ２０
由于Ｍａ２很小，可以忽略，则当Ｍａ０≥３时，ηｔ≥６４％；Ｍａ０≤１时，ηｔ≤１６．７％，所以，冲压发动机
要在高飞行马赫数时才适用。在低速飞行时，由于冲压比小，热效率低，推力小。若飞行速度为零，则
不能产生推力。
德国的Ｖ－１飞弹
早在 １９１３年，法国工程师雷恩
#
洛兰（Ｒｅｎé
ＬＯＲＩＮ，１８７７－１９３３）就得到了冲压式喷气发动机的
专利，比涡轮喷气发动机还早。只是在当时的低速下
根本无法工作，而且也缺乏所需的高温耐热材料而一
直没有在实际中实现。
Ｋｈ－３１系列空射型反舰导弹是俄罗斯２０世纪
９０年代问世的最新火箭／冲压发动机战术导弹，目前
有Ｋｈ－３１Ａ反舰型和 Ｋｈ－３１Ｐ反辐射型两种型号。
—２０２—
发射时先启动火箭发动机，当速度到达１．８马赫时再启动冲压发动机，并加速至３马赫。
由于该Ｋｈ－３１系列导弹的最高速度高达３马赫以上，因此颇受西方国家关注。波音公司总共想
要购买１００枚，但俄方担心美国将开发出对抗ＫＨ－３１的有效措施，只交付了１５枚。
超燃冲压发动机的研制和使用将会在航空航天领域引起一场革命！
亚燃冲压发动机（ＲＡＭＪＥＴ）
超燃冲压发动机（ＳＣＲＡＭＪＥＴ）
美国航空航天局（ＮＡＳＡ）采用超燃冲压发动机的 Ｘ－４３Ａ高超声速技术验证机于２００４年１１月
１６日创造了Ｍａ为９．８（１１３００ｋｍ／ｈ）的吸气式飞机飞行速度的最高纪录。
美国Ｘ－４３超燃冲压发动机的空中试验
“军事力量竞争正在向空天领域转移，军事力量建设不断向空天方向拓展。这种转移是大势所
趋，这种拓展是历史必然，这种发展不可逆转面对空天的军事化，没有足够的力量就没有发言权，只有
拥有强大的力量才能维护和保卫和平。”其中超燃冲压发动机的技术是关键。
—３０２—
沈维道《工程热力学》考点精讲及复习思路
考点六：火箭发动机循环
火箭发动机也是依靠喷气推进产生推力动力装置，不同的是它自身既带燃料，又带氧化 ，靠氧
化剂来助燃，不需要从周围大气层中吸取氧气。所以它不但能在大气层内，也可在大气层之外的宇宙
真空中工作，飞行高度没有限制。
０－２：推进剂在泵内的压缩过程，由于推进剂为液体，压缩过程中比体积变化很小，几乎为定容过
程，所消耗的泵功
ｗｔ０２ ＝－∫
ｐ２
ｐ０
ｖｄｐ≈０
３－５：气体膨胀过程所做技术功
ｗｔ３５ ＝－∫
ｐ５
ｐ３
ｖｄｐ＝ｈ３－ｈ５ ＝
１
２（ｃ
２
ｆ５－ｃ
２
ｆ３）≈
１
２ｃ
２
ｆ５
因此整个循环的循环功为
ｗ０ ＝ｗｔ０２＋ｗｔ５０≈
１
２ｃ
２
ｆ５
加热量ｑ１ ＝ｈ３－ｈ２≈ｈ３
热效率ηｔ＝
ｗ０
ｑ１
≈
ｈ３－ｈ５
ｈ３
＝１－
ｈ５
ｈ３
（理想气体、定比热容 ）ηｔ＝１－
Ｔ５
Ｔ３
＝１－ １
（
ｐ３
ｐ５
）
κ－１
κ
＝１－ １
πＮ
κ－１
κ
ηｔ＝１－
１
πＮ
κ－１
κ
火箭发动机的热效率随喷管内降压比πＮ ＝
ｐ３
ｐ５
增加而增大。
上式与燃气轮机理想循环热效率公式的形式完全相同，表明它们随循环参数的变化规律是相同
的。但注意这里的πＮ取决于火箭喷管的设计与制造，而燃气轮机中增压比π则取决于压气机的设计
与制造，对冲压发动机则取决于进口马赫数和扩压管的设计与制造，各个压比所对应的部件是不
同的。
—４０２—
长征系列火箭
１２０吨级液氧煤油发动机长时间试车
珠海航展上的“长征５号”重型运载火箭模型
Ｓａｔｕｒｎｆａｍｉｌｙ
—５０２—
沈维道《工程热力学》考点精讲及复习思路
Ａｒｉａｎｅ５是目前世界上运载能力最强的商用火箭
美国战神１－Ｘ火箭发射升空
内燃机与燃气轮机系统相比，单位质量的输出功率较低，如何增加其功率输出一直是一个研究
课题。
如果用专门的压气机把进气预先压缩一下就可以增加功率，这种方法称为增压。柴油机采用增
压后，功率可增加１０％～４０％甚至更多。
用增压办法最先是航空活塞式发动机用来补偿飞机在高空时的功率损失。后来增压发展成为内
燃机提高功率、减小尺寸的主要手段。目前在航空领域，有大量的轻型、超轻型飞机、无人机采用活塞
式发动机，也有使用涡轮增压的需要，特别是高空无人机，甚至需要多级增压。
用于增压的叶轮式压气机称为增压器（ｃｈａｒｇｅｒ）。它可以经由皮带，直接由内燃机的曲轴驱动，
称为机械增压 （ｓｕｐｅｒｃｈａｒｇｅｒ）。
如果增压器利用废气余压对涡轮驱动，一直膨胀到大气压，称为废气涡轮增压。简称涡轮增压
（ｔｕｒｂｏｃｈａｒｇｅｒ）。
由瑞士人波希（ＡｌｆｒｅｄＢüｃｈｉ，１８７９～１９５９）博士１９０５年提出并获得专利。世界上首台由废气驱动
的增压器于１９１２年问世。在１９１５年制造出了原型航空器发动机增压器。
１　 ＣｏｍｐｒｅｓｓｏｒＩｎｌｅｔ
２　 ＣｏｍｐｒｅｓｓｏｒＤｉｓｃｈａｒｇｅ
３　 Ｃｈａｒｇｅａｉｒｃｏｏｌｅｒ（ＣＡＣ）
４　 ＩｎｔａｋｅＶａｌｖｅ
５　 ＥｘｈａｕｓｔＶａｌｖｅ
６　 ＴｕｒｂｉｎｅＩｎｌｅｔ
７　 ＴｕｒｂｉｎｅＤｉｓｃｈａｒｇｅ
—６０２—
涡轮增压内燃机理想循环是由内燃机理想循环与燃气轮机理想循环叠加而成的。循环１２３４５１
的整个压力增大，气体密度增大，同样的气缸容积吸入更多空气量，做更多功。
无论用温度法还是热量法都可以明显看出采用废气涡轮增压后热效率增加。
为抑制爆震，一般的涡轮增压和机械增压发动机只能把压缩比设计得比普通自然吸气发动机低
很多。这种过低的压缩比会导致发动机在增压器（特别是涡轮增压）没有完全介入时（即发动机在低
转速时）燃烧效率很低，动力比普通自然吸气发动机所产生的动力小很多。这个矛盾已经被在１９９０
年获得专利的可变压缩比技术解决。
一般汽油机不采用增压，汽油机采用增压技术难度较大，采用增压的多是柴油机。但有了中间冷
却器降低气温，可以抑制爆震，加上电子控制技术的进步，近年来有越来越多的汽油机采用了增压
技术。
涡轮增压器的增压会给燃烧室提供更多的空气，使燃烧更彻底，排放更干净，满足环保要求。
今天在欧洲，涡轮增压器已经占到了５０％，在亚洲、美国也都在增长，已经成为提高动力性能的主
流方向。
典型例题
例１０－１０作图题：涡喷发动机由扩压器、燃烧室、涡轮、尾喷管组成，定性地画出涡喷发动机装置
示意图，并在ｐ－ｖ图上定性地画出各个不同的过程，并说明过程在哪个部件内完成，它的特点是什么。
（北航２００６年考研试题）
答：０－１进气道内压缩过程，降速增压。
１－２压气机内压缩过程，耗功增压。
２－３燃烧室内燃烧过程，吸热增温。
３－４涡轮内膨胀过程，降压降温。
４－５尾喷管内膨胀过程，降压增速。
—７０２—
沈维道《工程热力学》考点精讲及复习思路
例１０－１１计算题：一燃气轮机装置由一台压气机 Ｃ产生压缩空气，然后分两路进入两个燃烧室
Ａ和Ｂ中进行等压燃烧，燃气分别进入两台燃气轮机，其中燃气轮机Ⅰ发出的功率全部供应压气机，
燃气轮机Ⅱ发出功率Ｐ ＝２０００ｋＷ，压气机进口状态为：ｐ１＝０．１ＭＰａ，环境温度ｔ１＝２７℃；压气机增压
比π＝１０；两台燃气轮机进口处的燃气温度均为ｔ３＝１１８０℃，出口处的燃气温度均为ｔ４。燃气可近似
为空气，且ｃｐ＝１．００４ｋＪ／（ｋｇ·Ｋ），κ＝１．４。假设全部是可逆过程，且燃气轮机出口压力与压气机进
口压力相等；试求：
（１）每ｋｇ燃气在燃气轮机中所作的功ｗＴ；
（２）燃气轮机Ⅱ的质量流量ｑｍ，Ｂ；
（３）压气机每压缩ｋｇ空气所消耗的功ｗＣ；
（４）燃气轮机Ⅰ的质量流量ｑｍ，Ａ；
（５）每秒钟气体工质分别从两燃烧室吸收的热量Ｑ Ａ和Ｑ Ｂ；
（６）整个装置的热效率ηｔ。
（南航２０１０年考研试题）
解：１．物理模型：该燃气轮机循环中每一过程、参数均已确定，因此该循环确定，可按照分析循环
的方法求解。
２．数学模型及求解：
（１）燃气轮机涡轮功ｗＴⅠ ＝ｗＴⅡ ＝ｃｐ（Ｔ３－Ｔ４）
２．数学模型及求解：
燃气轮机出口温度
Ｔ４ ＝Ｔ３（
）κ－１
κ
＝１４５３×０．１
１．４－１
１．４
＝７５２．５８Ｋ＝４７９．５８℃
则　ｗＴⅠ ＝ｗＴⅡ ＝ｃｐ（ｔ３－ｔ４）＝１．００４×（１１８０－４７９．５８）＝７０３．２２ｋＪ／ｋｇ
—８０２—
（２）燃气轮机Ⅱ功率　Ｐ＝ｑｍ，ＢｗＴⅡ
则燃气轮机Ⅱ质量流量ｑｍ，Ｂ＝Ｐ／ｗＴⅡ ＝２０００／７０３．２２＝２．８４４　ｋｇ／ｓ
（３）压气机每压缩ｋｇ空气所消耗的功ｗＣ＝ｃｐ（Ｔ２－Ｔ１）
压气机出口温度Ｔ２ ＝Ｔ１（
ｐ２
ｐ１
）
κ－１
κ
＝３００×１０
１．４－１
１．４ ＝５７９．２１Ｋ＝３０６．２１℃
则　ｗＣ＝ｃｐ（ｔ２－ｔ１）＝１．００４×（３０６．２１－２７）＝２８０．３３　ｋＪ／ｋｇ
（４）燃气轮机Ⅰ功率平衡　ｑｍ，ＡｗＴⅠ ＝（ｑｍ，Ａ＋ｑｍ，Ｂ）ｗＣ
则燃气轮机Ⅰ质量流量ｑｍ，Ａ＝ｑｍ，Ｂｗ Ｃ／（ｗ ＴⅠ －ｗ Ｃ）＝２．８４４×２８０．３３／（７０３．２２－２８０．３３）１．
８８５ｋｇ／ｓ
（５）每秒钟气体工质分别从两燃烧室吸收的热量
Ｑ Ａ＝ｑｍ，Ａｃｐ（ｔ３－ｔ２）＝１．８８５×１．００４×（１１８０－３０６．２１）＝１６５３．８９ｋＷ
Ｑ Ｂ＝ｑｍ，Ｂｃｐ（ｔ３－ｔ２）＝２．８４４×１．００４×（１１８０－３０６．２１）＝２４９５．００ｋＷ
（６）整个装置的热效率ηｔ＝Ｐ／（Ｑ Ａ＋Ｑ Ｂ）＝２０００／（１６５３．８９＋２４９５．００）＝４８．２１％
４．讨论及结论：校验计算装置的热效率
ηｔ＝１－（ｑｍ，Ａ＋ｑｍ，Ｂ）ｃｐ（ｔ４－ｔ１）／（Ｑ Ａ＋Ｑ Ｂ）
ηｔ＝１－（１．８８５＋２．８４４）×１．００４×（４７９．５８－２７）／（１６５３．８９＋２４９５．００）＝４８．２１％
说明整个计算是正确的。
秘笈：若能从不同途径对结果进行验算是最好的。这样才构成解题的一个完整“循环”。
本章应注意的问题
１．熟练掌握一般循环的分析计算方法有助于对付任何循环，并加深对循环的理解。
２．工程中常见的循环如内燃机循环、燃气轮机循环、航空喷气发动机循环、火箭发动机循环、斯特
林循环，增压内燃机循环，等等，包括“回热”、“再热”的概念，只需作为循环的特例来看待就行了，并
对其热力性能的特点进行一些简单记忆，重要的还是“熟练掌握解决问题的方法”。得“道”者得
天下！
３．注重通过画图（ｐ－ｖ图、Ｔ－ｓ图等）的方法来帮助理解循环。画图是一种普遍适用的好方法。
４．工程热力学公式很多，但只要记住那些原始公式就行了。公式越“原始”，离“根”越近，适用范
围就越大。
—９０２—
沈维道《工程热力学》考点精讲及复习思路