概要信息：

目　录
第一章　 绪论 （２）
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
第二章　连续时间系统的时域分析 （７）
!!!!!!!!!!!!!!!!!!!!!!!!!
第三章　连续信号的正交分解 （１６）
!!!!!!!!!!!!!!!!!!!!!!!!!!!
第四章　连续时间系统的频域分析 （２３）
!!!!!!!!!!!!!!!!!!!!!!!!!
第五章　连续时间系统的复频域分析 （２８）
!!!!!!!!!!!!!!!!!!!!!!!!
第六章　连续时间系统的系统函数 （３９）
!!!!!!!!!!!!!!!!!!!!!!!!!
第七章　离散时间系统的时域分析 （４５）
!!!!!!!!!!!!!!!!!!!!!!!!!
第八章　离散时间系统的变换域分析 （５５）
!!!!!!!!!!!!!!!!!!!!!!!!
第九章　线性系统的状态变量分析 （６６）
!!!!!!!!!!!!!!!!!!!!!!!!!
一、教材说明
信号与线性系统（第四版）
高等教育出版社　 管致中 主编
二、辅导课阶段安排
１．教材重点、难点、考点精讲
２．名校考研真题及典型题的分类解析
３．课程内容的整体串讲及模拟试题分析
三、教材内容
第一章　绪论
第二章　连续时间系统的时域分析
第三章　连续信号的正交分解
第四章　连续时间系统的频域分析
第五章　连续时间系统的复频域分析
第六章　连续时间系统的系统函数
第七章　离散时间系统的时域分析
第八章　离散时间系统的变换域分析
第九章　线性系统的状态变量分析
—１—
管致中《信号与线性系统》考点精讲
第一章　绪论
【本章知识要点】
一、信号
１．信号的分类
２．信号的简单处理
（１）相加、相乘
（２）延时
（３）尺度变换　　　
（４）反褶（反转）
二、系统
１．系统的描述
２．系统的分类
（１）线性／非线性系统
（２）时不变／时变系统
（３）连续时间／离散时间系统
（４）因果／非因果系统
一、信号
１．信号的分类
①信号
确定信号{
随机信号
②信号
连续信号{
离散信号
③信号
能量信号：Ｅ＜
!
，Ｐ→０，Ｅ＝ｌｉｍ
ａ→!
∫
ａ
－ａ
ｆ（ｔ）２ｄｔ
功率信号：Ｐ＜
!
，Ｅ→０，Ｐ＝ｌｉｍ
ａ→!
１
２ａ∫
ａ
－ａ
ｆ（ｔ）２{ ｄｔ
④信号
周期信号：
连续：ｆ（ｔ）＝ｆ（ｔ＋ｍＴ）
离散：ｆ（ｋ）＝ｆ（ｋ＋ｍＮ）（ｍ＝０，±１，±２{
，…）
（功率信号）
非周期信号：可能是
能量信号（脉冲信号）
功率信号（ε（ｔ））
非能量 ／非功率信号（ｔε（ｔ
{{
））
—２—
周期信号的判别及周期Ｔ的确定
例：
１．ｆ（ｔ）＝ａｓｉｎｔ－ｂｓｉｎ３ｔ
（依据）周期信号的傅里叶级数展开：
ｆ（ｔ）＝
ａ０
２＋∑
!
ｎ＝１
（ａｎｃｏｓｎΩｔ＋ｂｎｓｉｎｎΩｔ），Ω ＝
２π
Ｔ

若找出各角频率的最大公约数Ω，则Ｔ＝２πΩ
若无法确定Ω，则ｆ（ｔ）为非周期信号
{
．
解　因为ω１ ＝１ω２ ＝３的最大公约数为Ω ＝１
故Ｔ＝２π
Ω
＝２π（ｓ）
２．ｆ（ｔ）＝ａｓｉｎ（５πｔ２）＋ｂｃｏｓ（
６πｔ
５）＋ｃｓｉｎ（
πｔ
７）
解　由于ω１ ＝
５π
２ ＝
１７５π
７０ω２ ＝
６π
５ ＝
８４π
７０ω３ ＝
π
７ ＝
１０π
７０
的最大公约数为Ω ＝π７０
故Ｔ＝２π
Ω
＝１４０（ｓ）
３．ｆ（ｔ）＝ａｓｉｎ（３ｔ）＋ｂｃｏｓ（πｔ）
解　①π≈３，该信号为周期信号
②π≈３．１４１…，该信号为非周期信号
能量信号与功率信号的判别
例　１．ｆ（ｔ）＝ｅ－αｔε（ｔ），α＞０．
２．ｆ（ｔ）＝Ａｃｏｓ（ω０ｔ＋θ）
２．信号的简单处理———都是针对时间“ｔ”而变换的
①相加：ｆ（ｔ）＝ｆ１（ｔ）＋ｆ２（ｔ）
②相乘：ｆ（ｔ）＝ｆ１（ｔ）·ｆ２（ｔ）
③时移：ｆ（ｔ）→ｆ（ｔ－ｔ０）
④尺度变换：ｆ（ｔ）→ｆ（ａｔ）
ａ＞１：ｆ（ｔ）在ｔ轴压缩到１ａ
０＜ａ＜１：ｆ（ｔ）在ｔ轴扩展到１ａ
{ 倍
⑤反褶（反转）：ｆ（ｔ）→ｆ（－ｔ）
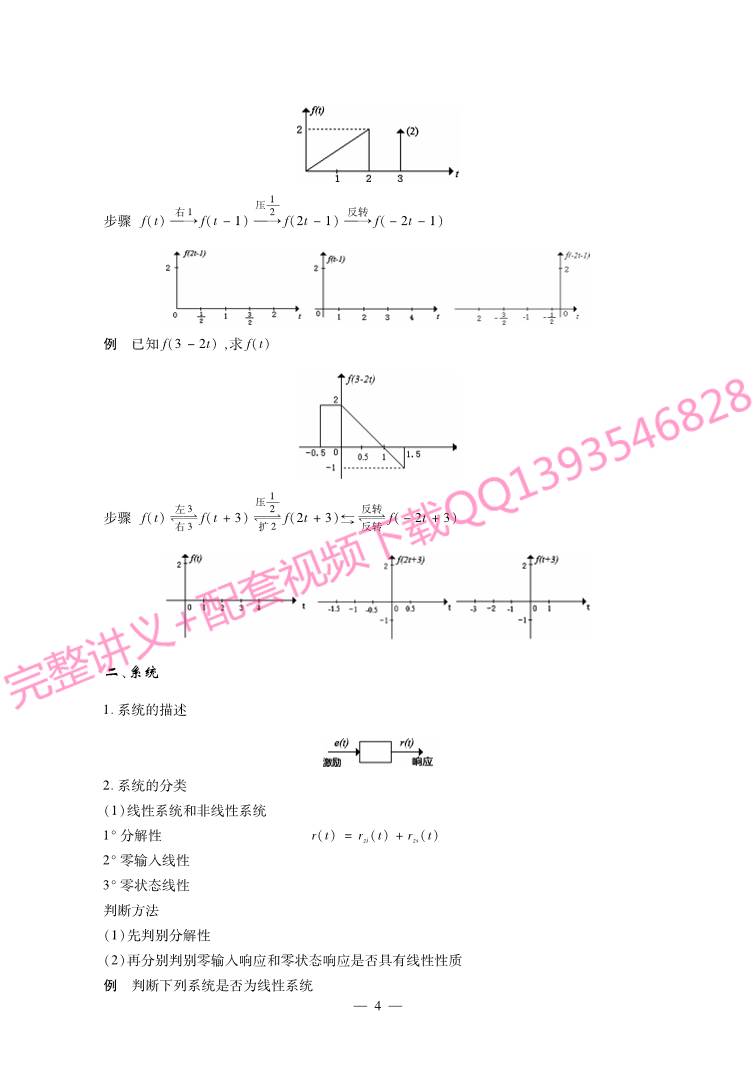
例　已知ｆ（ｔ），求ｆ（－２ｔ－１）。
—３—
管致中《信号与线性系统》考点精讲
步骤：ｆ（ｔ）
右
→
１
ｆ（ｔ－１）
压
→
１
２
ｆ（２ｔ－１） →
反转
ｆ（－２ｔ－１）
例　已知ｆ（３－２ｔ），求ｆ（ｔ）
步骤：ｆ（ｔ）
左３
右
幑幐３ｆ（ｔ＋３）
压
１
２
扩
幑幐２ｆ（２ｔ＋３）
反转
幑幐
反转
ｆ（－２ｔ＋３）
二、系统
１．系统的描述
２．系统的分类
（１）线性系统和非线性系统
１°分解性 ｒ（ｔ）＝ｒｚｉ（ｔ）＋ｒｚｓ（ｔ）
２°零输入线性
３°零状态线性
判断方法：
（１）先判别分解性
（２）再分别判别零输入响应和零状态响应是否具有线性性质
例　判断下列系统是否为线性系统
—４—
１．ｒ（ｔ）＝ｅ－ｔｘ（０）＋∫
ｔ
０
ｓｉｎｘｅ（ｘ）ｄｘ
２．ｒ（ｔ）＝ｅ（ｔ）ｘ（０）＋∫
ｔ
０
ｅ（ｘ）ｄｘ
３．ｒ（ｋ）＝（０．５）ｋｘ（０）＋ｅ（ｋ）ｅ（ｋ－２）
例　判断下列方程所描述的系统是否为线性系统
１．ｄｒ（ｔ）ｄｔ ＋ｒ（ｔ）＝ｅ（ｔ）＋５
２．ｄｒ（ｔ）ｄｔ ＋［ｒ（ｔ）］
２ ＝ｅ（ｔ）
３．ｄｒ（ｔ）ｄｔ ＋ｔｒ（ｔ）＋５∫
ｔ
－
!
ｒ（τ）ｄτ＝ｄｅ（ｔ）ｄｔ ＋ｅ（ｔ）
依据：在激励ｋ１ｅ１（ｔ）＋ｋ２ｅ２（ｔ）作用时，判断系统的响应是否为
ｋ１ｒ１（ｔ）＋ｋ２ｒ２（ｔ）
（２）时不变系统和时变系统
若ｅ（ｔ）→ｒｚｓ（ｔ）
则ｅ（ｔ－ｔ０）→ｒｚｓ（ｔ－ｔ０）
判断方法：先经系统再时移＝先时移再经系统
例　判断下列两个系统是否为时不变系统
１．ｒ（ｔ）＝ｃｏｓ［ｅ（ｔ）］　　　２．ｒ（ｔ）＝ｅ（ｔ）·ｃｏｓｔ
例　判断下列方程所描述的系统是否为时不变系统
１．ｄｒ（ｔ）ｄｔ ＋３ｒ（ｔ）＝ｅ（ｔ）
２．ｄ
２ｒ（ｔ）
ｄｔ２
＋ｔｄｄｔｒ（ｔ）＋ｒ（ｔ）＝２ｅ（ｔ）
３．ｒ（ｋ）＋４ｒ（ｋ－１）＋４ｒ（ｋ－２）＝ｅ（ｋ－１）
４．ｒ（ｋ）＋４ｒ（ｋ－１）＋ｒ（ｋ－１）ｒ（ｋ－２）＝ｅ（ｋ－１）
结论：若系统方程为常系数微分（差分）方程，则系统是时不变的。
（３）连续时间系统和离散时间系统
（４）因果系统和非因果系统
判断方法：响应不可能出现于激励之前
例　ｒ（ｔ）＝２ｅ（ｔ－３）所描述的系统为因果系统
ｒ（ｔ）＝２ｅ（ｔ＋３）所描述的系统为非因果系统
例　一具有两个初始条件ｘ１（０）、ｘ２（０）的线性时不变系统，其激励为 ｅ（ｔ），输出响应为 ｒ（ｔ）。
已知：
（１）当ｅ（ｔ）＝０，ｘ１（０）＝５，ｘ２（０）＝２时ｒ（ｔ）＝ｅ
－ｔ（７ｔ＋５），ｔ＞０
—５—
管致中《信号与线性系统》考点精讲
（２）当ｅ（ｔ）＝０，ｘ１（０）＝１，ｘ２（０）＝４时ｒ（ｔ）＝ｅ
－ｔ（５ｔ＋１），ｔ＞０
（３）当ｅ（ｔ）＝
１，ｔ＞０
０，ｔ＜{ ０
，ｘ１（０）＝１，ｘ２（０）＝１时ｒ（ｔ）＝ｅ
－ｔ（ｔ＋１），ｔ＞０
求：ｅ（ｔ）＝
３，ｔ＞０
０，ｔ＜{ ０
时的零状态响应。
—６—
第二章　连续时间系统的时域分析
本章知识要点
一、线性时不变系统的响应
古典解{
卷积解
二、奇异函数ε（ｔ），δ（ｔ），δ′（ｔ）
三、冲激响应ｈ（ｔ）
四、卷积积分
一、线性时不变系统的响应
１．古典解　
ｄｎｒ
ｄｔｎ
＋ａｎ－１
ｄｎ－１ｒ
ｄｔｎ－１
＋… ＋ａ１
ｄｒ
ｄｔ＋ａ０ｒ＝ｂｍ
ｄｍｅ
ｄｔｍ
＋ｂｍ－１
ｄｍ－１ｅ
ｄｔｍ－１
＋… ＋ｂ１
ｄｅ
ｄｔ＋ｂ０ｅ（２－１）
———ｎ阶线性常系数微分方程
ｒ（ｔ）＝齐次解＋特解
＝自由响应＋强迫响应
＝零输入响应＋零状态响应
（１）零输入响应ｒｚｉ（ｔ）
① 转移算子Ｈ（ｐ）
令
ｄ
ｄｔ＝ｐ，
ｄｎ
ｄｔｎ
＝ｐｎ
则式（２－１）表示为
ｐｎｒ＋ａｎ－１ｐ
ｎ－１ｒ＋… ＋ａ１ｐｒ＋ａ０ｒ＝ｂｍｐ
ｍｅ＋ｂｍ－１ｐ
ｍ－１ｅ＋… ＋ｂ１ｐｅ＋ｂ０ｅ
（ｐｎ＋ａｎ－１ｐ
ｎ－１＋… ＋ａ１ｐ＋ａ０）ｒ
Ｄ（ｐ） ＝
（ｂｍｐ
ｍ ＋ｂｍ－１ｐ
ｍ－１＋ｂ１ｐ＋ｂ０）ｅ
Ｎ（ｐ）
故
Ｄ（ｐ）ｒ（ｔ）＝Ｎ（ｐ）ｅ（ｔ）
ｒ（ｔ）＝Ｎ（ｐ）Ｄ（ｐ）ｅ（ｔ）
定义：转移算子Ｈ（ｐ）＝Ｎ（ｐ）Ｄ（ｐ）＝
ｂｍｐ
ｍ ＋ｂｍ－１ｐ
ｍ－１＋… ＋ｂ１ｐ＋ｂ０
ｐｎ＋ａｎ－１ｐ
ｎ－１＋… ＋ａ１ｐ＋ａ０
②ｒｚｉ（ｔ）的求解
Ｄ（ｐ）ｒ（ｔ）＝０———齐次方程
—７—
管致中《信号与线性系统》考点精讲
Ｄ（ｐ）＝０特征根λ１，λ２，…，λｎ（设均为单根）
故ｒ（ｔ）＝Ｃ１ｅλ１
ｔ＋Ｃ２ｅλ２
ｔ＋… ＋Ｃｎｅλｎ
ｔ
其中Ｃ１，Ｃ２，…Ｃｎ由ｎ个初始条件确定。
说明：λｉ（ｉ＝１，…，ｎ）称为响应中的自然频率
例１　已知系统的转移算子Ｈ（ｐ）＝ ｐ＋３
ｐ２＋３ｐ＋２
，未加激励的初始条件ｒ（０）＝１、ｒ′（０）＝２，求
该系统的零输入响应，并指出自然频率。
（２）零状态响应ｒｚｓ（ｔ）
Ｄ（ｐ）ｒ（ｔ）＝Ｎ（ｐ）ｅ（ｔ）
对于较复杂的激励ｅ（ｔ），求ｒｚｓ（ｔ）需要求解复杂的非齐次方程，计算量大，不常采用。　
２．卷积解
ｒｚｓ（ｔ）主要用卷积积分的方法来求，该部分在后续内容中详细讲解。
二、奇异函数ε（ｔ），δ（ｔ），δ′（ｔ）
１．单位阶跃函数ε（ｔ）
ε（ｔ）＝
１ ｔ＞０
不定义 ｔ＝０
０ ｔ＜
{
０
说明：
应用：用ε（ｔ）及ε（ｔ－ｔｉ）表示信号
例２：
２．单位冲激函数δ（ｔ）
—８—
定义：
δ（ｔ）＝０，ｔ≠０
δ（ｔ）＝!
，ｔ＝０
∫
!
－
!
δ（ｔ）ｄｔ＝




 １
性质：①
ｄε（ｔ）
ｄｔ ＝δ（ｔ）
∫
ｔ
－
!
δ（τ）ｄｔ＝ε（ｔ
{
）
②∫
!
－
!
δ（ｔ）ｄｔ＝１
③δ（ｔ）＝δ（－ｔ）
④ｆ（ｔ）δ（ｔ）＝ｆ（０）δ（ｔ）
ｆ（ｔ）δ（ｔ－ｔ０）＝ｆ（ｔ０）δ（ｔ－ｔ０）
⑤
∫
!
－
!
ｆ（ｔ）δ（ｔ）ｄｔ＝ｆ（０）
∫
!
－
!
ｆ（ｔ）δ（ｔ－ｔ０）ｄｔ＝ｆ（ｔ０
}
）
取样性
⑥δ（ａｔ）＝ １
ａδ（ｔ）
３．冲激偶δ′（ｔ）
性质：①δ′（－ｔ）＝－δ′（ｔ）
②ｆ（ｔ）δ′（ｔ）＝ｆ（０）δ′（ｔ）－ｆ′（０）δ（ｔ）
③∫
!
－
!
δ′（ｔ）ｄｔ＝０
④∫
ｔ
－
!
δ′（τ）ｄτ＝δ（ｔ）
例３　（１）ｙ１（ｔ）＝ｔ
ｄ
ｄｔ［ｅ
－ｔε（ｔ）］
（２）ｙ２（ｔ）＝∫
!
－
!
ｅ－ｔ［δ（ｔ）＋δ′（ｔ）］ｄｔ
（３）ｙ３（ｔ）＝∫
ｔ
－
!
（４＋τ３）δ（１－τ）ｄτ
—９—
管致中《信号与线性系统》考点精讲
（４）ｙ４（ｔ）＝∫
ｔ
－
!
（ｅ－τ＋τ）δ（τ２）ｄτ
三、冲激响应ｈ（ｔ）
１．定义
２．求解
（１）一般情况：
ｈ（ｎ）（ｔ）＋ａｎ－１ｈ
（ｎ－１）（ｔ）＋… ＋ａ１ｈ′（ｔ）＋ａ０ｈ（ｔ）＝δ（ｔ）
ｈ（０－）＝ｈ′（０－）＝… ＝ｈ（ｎ－１）（０－）＝０　ｔ０
则
ｈ（ｎ－１）（０＋）＝１
ｈ（ｎ－２）（０＋）＝…ｈ′（０＋）＝ｈ（０＋）＝０
（２）ｈ（ｎ）（ｔ）＋ａｎ＋１ｈ
（ｎ－１）＋… ＋ａ１ｈ′（ｔ）＋ａ０ｈ（ｔ）＝ｂｍδ
（ｍ）（ｔ）＋ｂｍ－１δ
（ｍ－１）（ｔ）＋… ＋ｂ１δ′（ｔ）＋
ｂ０δ（ｔ）
第一步：先求ｈ（ｎ）１ （ｔ）＋ａｎ－１ｈ
（ｎ－１）
１ （ｔ）＋… ＋ａ１ｈ′１（ｔ）＋ａ０ｈ１（ｔ）＝δ（ｔ）得到ｈ１（ｔ）
第二步：利用线性时不变系统的齐次性，可加性和微分性质，
有 ｈ（ｔ）＝ｂｍｈ１
（ｍ）（ｔ）＋ｂｍ－１ｈ
（ｍ－１）
１ （ｔ）＋… ＋ｂ１ｈ１′（ｔ）＋ｂ０ｈ１（ｔ）
例　已知系统的微分方程为ｒ″（ｔ）＋３ｒ′（ｔ）＋２ｒ（ｔ）＝ｅ（ｔ）＋４ｅ″（ｔ）－５ｅ（ｔ）求冲激响应ｈ（ｔ）。
解　 特征根λ１ ＝－１λ２ ＝－２
设δ（ｔ）单独作用的冲激响应为ｈ１（ｔ），则ｈ１（ｔ）＝（Ｃ１ｅ
－ｔ＋Ｃ２ｅ
－２ｔ）ε（ｔ）
又ｈ′１（０＋）＝１ｈ１（０＋）＝０
故
Ｃ１＋Ｃ２ ＝０
－Ｃ１－２Ｃ２ ＝
{ １
∴Ｃ１ ＝１Ｃ２ ＝－１
∴ｈ１（ｔ）＝（ｅ
－ｔ－ｅ－２ｔ）ε（ｔ）
系统的冲激响应为
ｈ（ｔ）＝ｈ１（ｔ）＋４ｈ″１（ｔ）－５ｈ１（ｔ）
＝δ′（ｔ）－３δ（ｔ）＋（８ｅ－２ｔ－ｅ－ｔ）ε（ｔ）＋４δ（ｔ）＋（４ｅ－ｔ－１６ｅ－２ｔ）ε（ｔ）－（５ｅ－ｔ－５ｅ－２ｔ）ε（ｔ）
＝δ′（ｔ）＋δ（ｔ）－３ｅ－２ｔε（ｔ）－２ｅ－ｔε（ｔ）
练习：
（１）求系统 ｄ
ｄｔｒ（ｔ）＋３ｒ（ｔ）＝２
ｄ
ｄｔｅ（ｔ）的冲激响应
（２）求系统 ｄ
３
ｄｔ３
ｒ（ｔ）＋ｄ
２
ｄｔ２
ｒ（ｔ）＋２ｄｄｔｒ（ｔ）＋２ｒ（ｔ）＝
ｄ２
ｄｔ２
ｅ（ｔ）＋２ｅ（ｔ）的冲激响应。
—０１—
３．阶跃响应ｒε（ｔ）
（１）定义：
（２）求解：
ε（ｔ）＝∫
ｔ
－
!
δ（τ）ｄτ→ｒε（ｔ）＝∫
ｔ
－
!
ｈ（τ）ｄτ＝∫
ｔ
０－
ｈ（τ）ｄτ
例　求上题中的ｒε（ｔ）。
四、卷积积分
１．叠加积分
ｅ（ｔ）＝∫
!
－
!
ｅ（τ）δ（ｔ－τ）ｄｔ
　　 ＝ｅ（ｔ）δ（ｔ）
　　　∫
!
－
!
ｅ（τ）ｈ（ｔ－τ）ｄτ＝ｒｚｓ（ｔ）
ｅ（ｔ）ｈ（ｔ）＝ｒｚｓ（ｔ）
即　ｒｚｓ（ｔ）＝ｅ（ｔ）ｈ（ｔ）＝∫
!
－
!
ｅ（τ）ｈ（ｔ－τ）———卷积积分
２．卷积积分的定义
ｆ（ｔ）＝ｆ１（ｔ）ｆ２（ｔ）＝∫
!
－
!
ｆ１（τ）ｆ２（ｔ－τ）ｄτ
３．卷积积分的物理意义
ｒ（ｔ）＝∫
!
－
!
ｅ（τ）ｈ（ｔ－τ）ｄτ
系统的零状态响应等于系统的激励与系统冲激响应的卷积积分。
４．卷积积分的性质
（１）卷积的代数运算
①交换律ｆ１（ｔ）ｆ２（ｔ）＝ｆ２（ｔ）ｆ１（ｔ）
②分配律ｆ１（ｔ）［ｆ２（ｔ）＋ｆ３（ｔ）］＝ｆ１（ｔ）ｆ２（ｔ）＋ｆ１（ｔ）ｆ３（ｔ）
③结合律［ｆ１（ｔ）ｆ２（ｔ）］ｆ３（ｔ）＝ｆ１（ｔ）［ｆ２（ｔ）ｆ３（ｔ）］
（２）函数与冲激函数的卷积
ｆ（ｔ）δ（ｔ）＝δ（ｔ）ｆ（ｔ）＝∫
!
－
!
δ（τ）ｆ（ｔ－τ）ｄτ＝ｆ（ｔ）
ｆ（ｔ）δ（ｔ－ｔ１）＝ｆ（ｔ－ｔ１）
ｆ（ｔ－ｔ１）δ（ｔ－ｔ２）＝ｆ（ｔ－ｔ１－ｔ２）
（３）卷积的微分与积分
①卷积的微分：若ｆ（ｔ）＝ｆ１（ｔ）ｆ２（ｔ）＝ｆ２（ｔ）ｆ１（ｔ）
—１１—
管致中《信号与线性系统》考点精讲
则
ｄｆ（ｔ）
ｄｔ ＝
ｄｆ１（ｔ）
ｄｔｆ２（ｔ）＝
ｄｆ２（ｔ）
ｄｔｆ１（ｔ）
②卷积的积分：
若ｆ（ｔ）＝ｆ１（ｔ）ｆ２（ｔ）＝ｆ２（ｔ）ｆ１（ｔ）
则∫
ｔ
－
!
ｆ（ｘ）ｄｘ＝［∫
ｔ
－
!
ｆ１（ｘ）ｄｘ］ｆ２（ｔ）＝［∫
ｔ
－
!
ｆ２（ｘ）ｄｘ］ｆ１（ｔ）
ｆ（ｔ）ε（ｔ）＝ｆ（ｔ）∫
ｔ
－
!
δ（τ）ｄτ＝∫
ｔ
－
!
ｆ（τ）ｄτ
③卷积的微分与积分：
ｆ１（ｔ）ｆ２（ｔ）＝
ｄ
ｄｔｆ１（ｔ）∫
ｔ
－
!
ｆ２（ｘ）ｄｘ＝［∫
ｔ
－
!
ｆ１（ｘ）ｄｘ］
ｄ
ｄｔｆ２（ｔ）
④函数延时后的卷积
若ｆ１（ｔ）ｆ２（ｔ）＝ｆ（ｔ）
则ｆ１（ｔ－ｔ１）ｆ２（ｔ－ｔ２）＝ｆ（ｔ－ｔ１－ｔ２）
５．卷积积分的计算
（１）用定义求
例　①求ε（ｔ）ε（ｔ）
②求ｅ－２ｔε（ｔ）ｅ－３ｔε（ｔ）
练习：求ε（ｔ）ｅλｔε（ｔ）
（２）图解法
ｆ（ｔ）＝ｆ１（ｔ）ｆ２（ｔ）＝∫
!
－
!
ｆ１（τ）ｆ２（ｔ－τ）ｄτ
步骤：
①ｆ１（ｔ）→ｆ１（τ）
②ｆ２（ｔ）→ｆ２（τ） →
反褶
ｆ２（－τ） →
时延
ｆ２（ｔ－τ）
③ 求∫
!
－
!
ｆ１（τ）ｆ２（ｔ－τ）ｄτ
例　ｆ１（ｔ）＝
１， ｔ＜１
０， ｔ＞{ １
，ｆ２（ｔ）＝
ｔ
２（０"ｔ"３），求ｆ１（ｔ）ｆ２（ｔ）。
解　①ｔ"－１
—２１—
ｆ１（τ）·ｆ２（ｔ－τ）＝０
故ｆ１（ｔ）ｆ２（ｔ）＝∫
!
－
!
ｆ１（τ）ｆ２（ｔ－τ）ｄτ＝０
② －１"ｔ"１
ｆ２（ｔ－τ）＝
ｔ－τ
２
故ｆ１（ｔ）ｆ２（ｔ）＝∫
ｔ
－１
１·ｔ－τ２ ｄτ＝（
ｔτ
２－
τ２
４）
ｔ
－１
＝ｔ
２
４＋
ｔ
２＋
１
４
③１"ｔ"２
ｔ－３≤－１
ｔ≥{ １
　１≤ｔ≤２
ｆ１（ｔ）ｆ２（ｔ）＝∫
１
－１
１·ｔ－τ２ ｄτ＝ｔ
④２"ｔ"４
－１≤ｔ－３≤１
ｔ≥{ １
　２≤ｔ≤４
ｆ１（ｔ）ｆ２（ｔ）＝∫
１
ｔ－３
１·ｔ－τ２ ｄｔ＝－
ｔ２
４＋
ｔ
２＋２
—３１—
管致中《信号与线性系统》考点精讲
⑤ｔ４
ｆ１（ｔ）ｆ２（ｔ）＝０
波形：
ｆ１（ｔ）ｆ２（ｔ）＝
ｔ２
４＋
ｔ
２＋
１
４， －１
"
ｔ
"
１
ｔ， １
"
ｔ
"
２
－ｔ
２
４＋
ｔ
２＋２， ２
"
ｔ
"
４
０， 其它









ｔ
说明：积分上下限和卷积结果区间的确定
１．积分上下限：由ｆ１（τ）·ｆ２（ｔ－τ）≠０的范围确定
２．卷积结果区间
一般规律：
　　　　　　　　　下限　　上限
ｆ１（ｔ）　　　　　　　［Ａ　　　Ｂ］
ｆ２（ｔ）　　　　　　　［Ｃ　　　Ｄ］
ｆ１（ｔ）ｆ２（ｔ）　　［Ａ＋Ｃ　　　Ｂ＋Ｄ］
例　已知ｆ１（ｔ），ｆ２（ｔ）的波形，令ｆ（ｔ）＝ｆ１（ｔ）ｆ２（ｔ），试求ｆ（３）。
（３）用性质求
例　①求ε（ｔ－１）ε（ｔ－５）
②已知ｅ（ｔ），ｈ（ｔ），求ｒ（ｔ）＝ｅ（ｔ）ｈ（ｔ）。
—４１—
—５１—
管致中《信号与线性系统》考点精讲
第三章　连续信号的正交分解
【本章知识要点】
一、周期信号的分析———傅里叶级数
二、非周期信号的分析———傅里叶变换
定义
常用变换对{
性质
三、周期信号的傅里叶变换
四、帕塞瓦尔定理
一、周期信号的分析———傅里叶级数
１．三角傅里叶级数
ｆ（ｔ）＝
ａ０
２＋∑
!
ｎ＝１
［ａｎｃｏｓ（ｎΩｔ）＋ｂｎｓｉｎ（ｎΩｔ）］
＝
ａ０
２＋∑
!
ｎ＝１
Ａｎｃｏｓ（ｎΩｔ＋φｎ）
Ω ＝２πＴ：基波频率
Ｔ：周期
ｎΩ：谐波频率
ａ０
２：直流分量
任意一个代表信号的函数可以用直流分量和一系列谐波分量之和来表示。
ａｎ ＝
２
Ｔ∫
ｔ１＋Ｔ
ｔ１
ｆ（ｔ）ｃｏｓ（ｎΩｔ）ｄｔａ０ ＝
２
Ｔ∫
ｔ１＋Ｔ
ｔ１
ｆ（ｔ）ｄｔ
ｂｎ ＝
２
Ｔ∫
ｔ１＋Ｔ
ｔ１
ｆ（ｔ）ｓｉｎ（ｎΩｔ）ｄｔ（ｎ＝１，２，３…）
ａｎ ＝Ａｎｃｏｓφｎ
ｂｎ ＝－Ａｎｓｉｎφ
{
ｎ
　　
Ａｎ ＝ ａ２ｎ＋ｂ
２
槡 ｎ
φｎ ＝－ａｒｃｔａｎ（
ｂｎ
ａｎ
{ ）
ａｎ ＝ａ－ｎ
ｂｎ ＝－ｂ
{
－ｎ
　　
Ａｎ ＝Ａ－ｎ（幅度频谱）
φｎ ＝－φ－ｎ（相位频谱
{
）
说明：只有函数ｆ（ｔ）满足Ｄｉｒｉｃｈｌｅｔ条件时，ｆ（ｔ）才可以分解为谐波分量。
—６１—
例　试画出ｆ（ｔ）＝１＋２ｓｉｎπｔ－３ｃｏｓ（３πｔ－π６）＋４ｃｏｓ（５πｔ＋
π
３）的单边谱。
２．指数傅里叶级数
ｆ（ｔ）＝１２∑
!
ｎ＝－
!
Ａｎ
·
ｅｊｎΩｔ
其中Ａｎ
·
＝Ａｎｅ
ｊφｎ ＝２Ｔ∫
ｔ１＋Ｔ
ｔ１
ｆ（ｔ）ｅ－ｊｎΩｔｄｔ
Ａｎ ＝Ａ－ｎ（双边幅度谱）
φｎ ＝－φ－ｎ（双边相位谱
{
）
例　
说明：周期信号频谱的特点：离散性、谐波性、收敛性。
３．函数的偶、奇性及其与谐波含量的关系
（１）ｆ（ｔ）为偶函数ｆ（ｔ）＝ｆ（－ｔ）
ａｎ ＝
２
Ｔ∫
ｔ１＋Ｔ
ｔ１
ｆ（ｔ）ｃｏｓ（ｎΩｔ）ｄｔ
ｂｎ ＝
}
０
包含直流分量，余弦分量
（２）ｆ（ｔ）为奇函数ｆ（ｔ）＝－ｆ（－ｔ）
—７１—
管致中《信号与线性系统》考点精讲
ａｎ ＝０ａ０ ＝０
ｂｎ ＝
２
Ｔ∫
ｔ１＋Ｔ
ｔ１
ｆ（ｔ）ｓｉｎ（ｎΩｔ） }ｄｔ包含正弦分量
（３）ｆ（ｔ）为奇谐函数ｆ（ｔ）＝－ｆ（ｔ＋Ｔ２）
ｎ为奇数：ａｎ≠０，ｂｎ≠０
ｎ为偶数：ａｎ ＝ｂｎ ＝
}０
只包含奇次谐波分量
（４）ｆ（ｔ）为偶谐函数ｆ（ｔ）＝ｆ（ｔ＋Ｔ２）
ｎ为偶数：ａｎ≠０ｂｎ≠０
ｎ为奇数：ａｎ ＝ｂｎ ＝
}０ 只包含偶次谐波分量
例　利用信号的奇偶性，判断下图中信号的傅里叶级数所包含的分量。
例　已知周期信号ｆ（ｔ）前四分之一周期的波形，按以下条件绘出整个周期的信号波形：ｆ（ｔ）是ｔ
的偶函数，其傅里叶级数只有偶次谐波。
二、非周期信号的分析———傅里叶变换
１．定义
Ｆ（ｊω）＝∫
!
－
!
ｆ（ｔ）ｅ－ｊωｔｄｔ
ｆ（ｔ）＝ １２π∫
!
－
!
Ｆ（ｊω）ｅｊωｔｄω
　　　　　ｆ（ｔ）Ｆ（ｊω）
—８１—
频谱密度函数Ｆ（ｊω）＝ Ｆ（ｊω）ｅｊφ（ω）　
说明：非周期信号ｆ（ｔ）傅里叶变换存在的充分条件：∫
!
－
!
ｆ（ｔ）ｄｔ＜!
２．常用傅里叶变换对
（１）δ（ｔ）１
（２）１２πδ（ω）
（３）δ′（ｔ）ｊω
（４）ε（ｔ）πδ（ω）＋１ｊω
（５）ｅ－αｔε（ｔ） １
α＋ｊω
（α＞０）
（６）ｅ－α ｔε（ｔ） ２α
α２＋ω２
（α＞０）
（７）ｇτ（ｔ）τＳａ（
ωτ
２）
（８）ｓｇｎ（ｔ） ２ｊω
（９）ｃｏｓω０ｔπ［δ（ω＋ω０）＋δ（ω－ω０）］
ｓｉｎω０ｔｊπ［δ（ω＋ω０）－δ（ω－ω０）］
３．傅里叶变换的性质
（１）线性　ａ１ｆ１（ｔ）＋ａ２ｆ２（ｔ）ａ１Ｆ１（ｊω）＋ａ２Ｆ２（ｊω）
（２）延时ｆ（ｔ±ｔ０）Ｆ（ｊω）ｅ
±ｊωｔ０
（３）移频ｆ（ｔ）ｅｊωｃｔＦ［ｊ（ω－ωｃ）］
应用：ｆ（ｔ）ｃｏｓωｃｔ
１
２ Ｆ［ｊ（ω＋ωｃ）］＋Ｆ［ｊ（ω－ωｃ
{ }）］
ｆ（ｔ）ｓｉｎωｃｔｊ
１
２ Ｆ［ｊ（ω＋ωｃ）］－Ｆ［ｊ（ω－ωｃ
{ }）］
例　求该信号的傅里叶变换
ｆ１（ｔ）＝ｇ２π（ｔ）ｃｏｓ（５ｔ）
（４）尺度变换
—９１—
管致中《信号与线性系统》考点精讲
ｆ（ａｔ） １
ａＦ（ｊ
ω
ａ）
例　求ｅ－２ｔε（ｔ＋１）的傅里叶变换
（５）奇偶性
Ｆ（ｊω）的奇偶性
Ｆ（ｊω）＝∫
!
－
!
ｆ（ｔ）ｅ－ｊωｔｄｔ＝∫
!
－
!
ｆ（ｔ）ｃｏｓ（ωｔ）ｄｔ－ｊ∫
!
－
!
ｆ（ｔ）ｓｉｎ（ωｔ）ｄｔ
＝Ｒ（ω）＋ｊＸ（ω）
＝ Ｆ（ｊω）ｅｊφ（ω）
①　　　　　　　　　　　　②
Ｒ（ω）＝Ｒ＝（－ω）
Ｘ（ω）＝－Ｘ（－ω{
）
　　　　　　　
Ｆ（ｊω） ＝ Ｆ（－ｊω）
φ（ω）＝－φ（－ω{
）
（６）对称性　　若ｆ（ｔ）Ｆ（ｊω）　则Ｆ（ｊｔ）２πｆ（－ω）
例１　求Ｓａ（πｔ）的傅里叶变换
例２　求 １ｔ的傅里叶变换
例３　 求 ２α
α２＋ｔ２
的傅里叶变换
（７）时域微分
ｄｆ（ｔ）
ｄｔｊωＦ（ｊω）
ｄｎｆ（ｔ）
ｄｔｎ
（ｊω）ｎＦ（ｊω）
例１　δ′（ｔ）ｊω
例２　求三角函数的频谱密度函数
（８）时域积分
∫
ｔ
－
!
ｆ（τ）ｄτπＦ（０）δ（ω）＋Ｆ（ｊω）ｊω
—０２—
若Ｆ（０）＝０，　 则∫
ｔ
－
!
ｆ（τ）ｄτＦ（ｊω）ｊω
其中Ｆ（０）＝Ｆ（ｊω）ω＝０ ＝∫
!
－
!
ｆ（ｔ）ｄｔ　
例　求ｆ（ｔ）的傅里叶变换
（９）频域微分（－ｊｔ）ｆ（ｔ）ｄＦ（ｊω）ｄω
例　求ｔε（ｔ）的傅里叶变换
（１０）卷积定理
时域卷积定理：ｆ１（ｔ）ｆ２（ｔ）Ｆ１（ｊω）Ｆ２（ｊω）
频域卷积定理：ｆ１（ｔ）ｆ２（ｔ）
１
２π
Ｆ１（ｊω）Ｆ２（ｊω）
例１　求下图信号的傅里叶变换
例２　利用频域卷积定理求ｃｏｓ（ωｃｔ）ε（ｔ）的傅里叶变换
三、周期信号的傅里叶变换
Ｆ（ｊω）＝π∑
!
ｎ＝－
!
Ａｎ
·
δ（ω－ｎΩ）Ω ＝２πＴ
周期信号的频谱函数是一个冲激序列，各个冲激位于各次谐波频率处，各冲激的强度分别等于各
次谐波复振幅的π倍。
例　求δＴ（ｔ）的傅里叶变换
练　求ｆ（ｔ）的傅里叶变换
—１２—
管致中《信号与线性系统》考点精讲
四、帕塞瓦尔定理
１．周期信号的功率
Ｐ＝ｆ２（ｔ）＝（
Ａ０
２）
２
＋１２∑
!
ｎ＝１
Ａ２ｎ ＝∑
!
ｎ＝－
!
（
Ａｎ
２）
２
周期信号的平均功率在各次谐波中分布，其功率等于直流功率与各次谐波功率之和。
２．非周期信号的能量
Ｗ ＝∫
!
－
!
ｆ２（ｔ）ｄｔ＝ １２π∫
!
－
!
Ｆ（ｊω）
２
ｄω　
例　已知ｆ（ｔ）的频谱函数为Ｆ（ｊω），求下列各值。
（１）∫
!
－
!
Ｆ（ｊω）ｄω
（２）∫
!
－
!
Ｆ（ｊω）２ｄω
—２２—
第四章　连续时间系统的频域分析
【本章知识要点】
一、频率响应Ｈ（ｊω）及在系统分析中的应用
二、调制与解调
三、无失真传输条件
一、频率响应Ｈ（ｊω）及在系统分析中的应用
１．频率响应Ｈ（ｊω）
（１）定义
Ｅ（ｊω）·Ｈ（ｊω）＝Ｒ（ｊω）
Ｈ（ｊω）＝Ｒ（ｊω）Ｅ（ｊω）
＝Ｆ［ｈ（ｔ）］　　　　Ｈ（ｊω）＝ Ｈ（ｊω）ｅｊφ（ω）
Ｈ（ｊω） ～ω幅频响应
φ（ω）～ω{
相频响应
（２）求解方法
①已知系统方程ｒ″（ｔ）＋３ｒ′（ｔ）＋２ｒ（ｔ）＝２ｅ′（ｔ）＋３ｅ（ｔ）
②已知系统结构
２．零状态响应
Ｒｚｓ（ｊω）＝Ｅ（ｊω）·Ｈ（ｊω）
ｒｚｓ（ｔ）＝Ｆ
－１［Ｒｚｓ（ｊω）］
例１　某系统的输入ｅ（ｔ）与输出ｒｚｓ（ｔ）的关系为ｒｚｓ（ｔ）＝
１
π∫
!
－
!
ｅ（τ）
ｔ－τ
ｄτ
（１）求系统的频率响应Ｈ（ｊω）
—３２—
管致中《信号与线性系统》考点精讲
（２）证明ｒｚｓ（ｔ）与ｅ（ｔ）的能量相等
例２　已知Ｈ（ｊω）＝ Ｈ（ｊω）ｅｊφ（ω），激励ｅ（ｔ）＝２＋∑
!
ｎ＝１
１
ｎｃｏｓ（ｎｔ）求零状态响应ｒ（ｔ）。
例３　求ｅ（ｔ）＝ｓｉｎ（２πｔ）２πｔ
的信号通过图（ａ）系统后的输出，系统中理想带通滤波器的传输特性如
图（ｂ）示，其相位特性φ（ω）＝０。
例４　如图所示系统，已知ｈ１（ｔ）＝
ｄ
ｄｔ［
ｓｉｎ（２ｔ）
２πｔ
］，Ｈ２（ｊω）＝ｅ
－ｊπω
ｈ３（ｔ）＝ε（ｔ），ｈ４（ｔ）＝
ｓｉｎ（６ｔ）
πｔ
。
（１）求复合系统的频率响应Ｈ（ｊω）和冲激响应ｈ（ｔ）；
（２）若输入ｅ（ｔ）＝ｓｉｎ（４ｔ）＋ｃｏｓ（ｔ），求系统的零状态响应ｒ（ｔ）。
二、调制与解调
１．调制与解调的概念
① 调制：由待传输的低频电信号（调制信号），去控制另一个高频振荡信号的振幅、频率或初相位
等参数之一。
ａ０（ｔ）＝Ａ０ｃｏｓ（ωｃｔ＋φ０）
幅度调制（ＡＭ）：用调制信号去控制高频振荡信号的振幅，使振幅不再是常数，而是按调制信号的
规律在变化，该调变振幅的过程成为～。
频率调制（ＦＭ）：调变的是高频振荡信号的频率
相位调制（ＰＭ）：调变的是高频振荡信号的初相位
另外：脉冲调制：用调制信号去控制一个脉冲序列的脉冲幅度，脉冲宽度或脉冲位置等参数之一。
说明：
ａ０（ｔ）＝Ａ０ｃｏｓ（ωｃｔ＋φ０）———载波
—４２—
ωｃ ＝２πｆｃ———载频
② 解调：从已调信号中恢复或取出调制信号的过程，是调制的逆过程。
２．抑制载频调幅（ＡＭ－ＳＣ）
①调制：
ａ（ｔ）＝ｅ（ｔ）ｃｏｓ（ωｃｔ）
Ａ（ｊω）＝１２ Ｅ［ｊ（ω＋ωｃ）］＋Ｅ［ｊ（ω－ωｃ
{ }）］
频谱图：
频带宽度：ＢＡ ＝２ωｍ
② 解调：
ｃ（ｔ）＝１２ｅ（ｔ）
ｂ（ｔ）＝ａ（ｔ）ｃｏｓωｃｔ＝ｅ（ｔ）ｃｏｓ
２（ωｃｔ）＝
１
２［ｅ（ｔ）＋ｅ（ｔ）ｃｏｓ（２ωｃｔ）］
Ｂ（ｊω）＝１２Ａ［ｊ（ω＋ωｃ）］＋
１
２Ａ［ｊ（ω－ωｃ）］
＝１４Ｅ［ｊ（ω＋２ωｃ）］＋
１
２Ｅ（ｊω）＋
１
４Ｅ［ｊ（ω－２ωｃ）］
—５２—
管致中《信号与线性系统》考点精讲
说明：调制解调中的载波必须严格地同频同相，否则无法恢复原信号的频谱结构，从而发生信号
失真。
３．振幅调制（ＡＭ）
ａ（ｔ）＝［Ａ０＋ｅ（ｔ）］ｃｏｓ（ωｃｔ）＝Ａ０ｃｏｓ（ωｃｔ）＋ｅ（ｔ）ｃｏｓ（ωｃｔ）
Ａ（ｊω）＝πＡ０［δ（ω＋ωｃ）＋δ（ω－ωｃ）］＋
１
２Ｅ［ｊ（ω＋ωｃ）］＋
１
２Ｅ［ｊ（ω－ωｃ）］
频带宽度ＢＡ ＝２ωｍ
说明：Ａ０ ｅ（ｔ）ｍａｘ
若ｅ（ｔ）＝∑
ｎ
１
Ｅｎｍｃｏｓ（Ωｎｔ＋φｎ）
则 　ａ（ｔ）＝［Ａ０＋ｅ（ｔ）］ｃｏｓ（ωｃｔ）
＝［Ａ０＋∑
ｎ
１
Ｅｎｍｃｏｓ（Ωｎｔ＋φｎ）］ｃｏｓ（ωｃｔ）
＝Ａ０［１＋∑
ｎ
１
ｍｎｃｏｓ（Ωｎｔ＋φｎ）］ｃｏｓ（ωｃｔ）
ｍｎ ＝
Ｅｎｍ
Ａ０
：表示调制信号中ｎ次谐波分量对载频幅度控制程度，
称为部分调幅系数。
令φｎ ＝０　则ｅ（ｔ）＝∑
ｎ
１
Ｅｎｍｃｏｓ（Ωｎｔ）
—６２—
Ｅ（ｊω）＝∑
ｎ
１
πＥｎｍ［δ（ω＋Ωｎ）＋δ（ω－Ωｎ）］
调幅信号的频谱
Ａ（ｊω）＝πＡ０［δ（ω＋ω０）＋δ（ω－ωｃ）］＋∑
ｎ
１
πＥｎｍ
２ ［δ（ω＋Ωｎ＋ωｃ）＋δ（ω＋Ωｎ－ωｃ）］
＋∑
ｎ
１
πＥｎｍ
２ ［δ（ω－Ωｎ＋ωｃ）＋δ（ω－Ωｎ－ωｃ）］
调幅信号的功率：载频功率Ｐｃ＝
１
２Ａ０
２
边频功率Ｐｓ＝∑
!
１
ｍ２ｎ
２Ｐｃ
例　有一调幅信号为ａ（ｔ）＝Ａ［１＋０．３ｃｏｓ（ω１ｔ）＋０．１ｃｏｓ（ω２ｔ）］ｓｉｎ（ωｃｔ），其中：ω１＝２π×５×
１０３ｒａｄ／ｓ、ω２ ＝２π×３×１０
３ｒａｄ／ｓ、ωｃ ＝２π×４５×１０
６ｒａｄ／ｓＡ＝１００Ｖ，试求：
（１）部分调幅系数；
（２）此调幅信号加到１ｋΩ电阻上产生的平均功率、载波功率与边频功率。
三、无失真传输条件
ｒ（ｔ）＝Ｋｅ（ｔ－ｔ０）
无失真传输的条件：
１．时域：ｈ（ｔ）＝Ｋδ（ｔ－ｔ０）
２．频域：Ｈ（ｊω）＝Ｋｅ－ｊωｔ０
Ｈ（ｊω） ＝Ｋ
φ（ω）＝－ωｔ{
０
—７２—
管致中《信号与线性系统》考点精讲
第五章　连续时间系统的复频域分析
【本章知识要点】
一、单边拉普拉斯变换
二、常用信号的Ｆ（ｓ）
三、拉普拉斯变换的基本性质
四、拉普拉斯反变换
五、线性系统的拉普拉斯变换分析法
六、双边拉普拉斯变换
七、信号流图
八、系统模拟
一、单边拉普拉斯变换
为什么引入拉普拉斯变换？
１．定义
Ｆ（ｓ）＝∫
!
０
ｆ（ｔ）ｅ－ｓｔｄｔ
ｆ（ｔ）＝［１２πｊ∫
σ＋ｊ!
σ－ｊ!
Ｆ（ｓ）ｅｓｔｄｓ］ε（ｔ）
或ｆ（ｔ）Ｆ（ｓ）
２．收敛区（收敛域）
把ｆ（ｔ）ｅ－σｔ满足绝对可积的σ值的范围称为收敛区通常ｆ（ｔ）是指数阶函数且有分段连续的性质
单边拉普拉斯变换的收敛区为某条直线的右半边平面
—８２—
ｌｉｍ
ｔ→!
ｆ（ｔ）ｅ－σｔ＝０？，σ＞σ０
σ＞σ０：收敛条件
σ０：收敛坐标
（１）单个脉冲信号：
收敛区为全Ｓ平面
（２）单位阶跃信号
ｌｉｍ
ｔ→!
［ε（ｔ）ｅ－σｔ］＝０？，σ＞０
（３）指数函数ｅαｔ
ｌｉｍ
ｔ→!
［ｅαｔ·ｅ－σｔ］＝ｌｉｍ
ｔ→!
ｅ（α－σ）ｔ＝０？，σ＞α
二、常用信号的Ｆ（ｓ）
若ｆ（ｔ）的拉普拉斯变换收敛区包括ｊω轴在内，则Ｆ（ｓ）＝Ｆ（ｊω）ｊω＝ｓ；若ｆ（ｔ）的拉普拉斯变换收
敛区不包括ｊω轴在内，则Ｆ（ｓ）必须由积分式求得。
１．δ（ｔ）１
２．ｅαｔε（ｔ） １
ｓ－α
３．ε（ｔ） １ｓ
４．ｔｎε（ｔ） ｎ！
ｓｎ＋１
　
５．ｔε（ｔ） １
ｓ２
，ｔ２ε（ｔ） ２
ｓ３
６．ｓｉｎ（βｔ）ε（ｔ） β
ｓ２＋β２
７．ｃｏｓ（βｔ）ε（ｔ） ｓ
ｓ２＋β２
８．ｓｉｎｈ（βｔ）ε（ｔ） β
ｓ２－β２
９．ｃｏｓｈ（βｔ）ε（ｔ） ｓ
ｓ２－β２
１０．δ′（ｔ）ｓ
三、拉普拉斯变换的基本性质
１．线性
设ｆ１（ｔ）Ｆ１（ｓ）ｆ２（ｔ）Ｆ２（ｓ），
则ａ１ｆ１（ｔ）＋ａ２ｆ２（ｔ）ａ１Ｆ１（ｓ）＋ａ２Ｆ２（ｓ）
例　求δ（ｔ）＋ｅ－２ｔε（ｔ）的拉普拉斯变换
—９２—
管致中《信号与线性系统》考点精讲
２．尺度变换
设ｆ（ｔ）Ｆ（ｓ），则ｆ（ａｔ） １ａＦ（
ｓ
ａ），（ａ＞０）
例　求ｆ（ｔ）＝ｃｏｓ（２ｔ）ε（ｔ）的拉普拉斯变换
３．时间平移
设ｆ（ｔ）Ｆ（ｓ），则ｆ（ｔ－ｔ０）ε（ｔ－ｔ０）Ｆ（ｓ）ｅ
－ｓｔ０，ｔ００
例　求下图中ｆ（ｔ）的拉普拉斯变换
４．频率平移
设ｆ（ｔ）Ｆ（ｓ），则ｆ（ｔ）ｅｓ０ｔＦ（ｓ－ｓ０）
例１　已知ｔε（ｔ） １
ｓ２
，则ｅ－ｔｔε（ｔ）
例２　已知ｃｏｓ（２ｔ）ε（ｔ） ｓ
ｓ２＋４
，则ｅ－２ｔｃｏｓ（２ｔ）ε（ｔ）
５．时域微分
设ｆ（ｔ）Ｆ（ｓ）
则
ｄｎｆ（ｔ）
ｄｔｎ
ｓｎＦ（ｓ）－ｓｎ－１ｆ（０－）－ｓ
ｎ－２ｆ′（０－）－… －ｆ（ｎ－１）（０－）ｄｆ（ｔ）ｄｔｓＦ（ｓ）－ｆ（０－）
ｄ２ｆ（ｔ）
ｄｔ２
ｓ２Ｆ（ｓ）－ｓｆ（０－）－ｆ′（０－）
若ｆ（ｔ）为因果信号，即ｔ＜０时ｆ（ｔ）＝０，则　ｄ
ｎｆ（ｔ）
ｄｔｎ
ｓｎＦ（ｓ）
例　求ｆ（ｔ）＝ｄ
２
ｄｔ２
［ｓｉｎ（πｔ）ε（ｔ）］的拉普拉斯变换
６．时域积分
设ｆ（ｔ）Ｆ（ｓ），则∫
ｔ
０
ｆ（τ）ｄτＦ（ｓ）ｓ
∫
ｔ
－
!
ｆ（τ）ｄτＦ（ｓ）ｓ ＋
∫
０
－
!
ｆ（τ）ｄτ
ｓ
—０３—
例　求ｆ（ｔ）的拉普拉斯变换
７．复频域微分
设ｆ（ｔ）Ｆ（ｓ），则（－ｔ）ｆ（ｔ）ｄＦ（ｓ）ｄｓ
例　求ｔ２ｅ－ｔε（ｔ）的拉普拉斯变换
８．初值定理
（１）设ｆ（ｔ）及ｆ′（ｔ）存在，并有拉普拉斯变换，则
ｆ（０＋）＝ｌｉｍ
ｔ→０＋
ｆ（ｔ）＝ｌｉｍ
ｓ→!
ｓＦ（ｓ）（Ｆ（ｓ）：真分式）
（２）若ｆ（ｔ）在ｔ＝０处有冲激及其导数，则
ｆ（ｔ）ａ０＋ａ１ｓ＋… ＋ａｐｓ
ｐ＋Ｆｐ（ｓ）　 （Ｆｐ（ｓ）：真分式）
那么ｆ（０＋）＝ｌｉｍ
ｓ→!
ｓＦｐ（ｓ）
９．终值定理
设ｆ（ｔ）及ｆ′（ｔ）存在，并有拉普拉斯变换，且Ｆ（ｓ）的所有极点都位于ｓ左半平面内（包括在原点
处的单极点）
则ｆ（
!
）＝ｌｉｍ
ｔ→!
ｆ（ｔ）＝ｌｉｍ
ｓ→０
ｓＦ（ｓ）
例　求Ｆ（ｓ）＝ ２ｓ＋３
（ｓ＋１）２
原函数的初值ｆ（０＋）和终值ｆ（!）
１０．卷积定理
时域卷积：ｆ１（ｔ）ｆ２（ｔ）Ｆ１（ｓ）·Ｆ２（ｓ）
复频域卷积：ｆ１（ｔ）ｆ２（ｔ）
１
２πｊ
Ｆ１（ｓ）Ｆ２（ｓ）
应用：ｒｚｓ（ｔ）＝ｅ（ｔ）ｈ（ｔ）
Ｒｚｓ（ｓ）＝Ｅ（ｓ）Ｈ（ｓ）
四、拉普拉斯反变换
ｆ（ｔ）＝［１２πｊ∫
σ＋ｊ!
σ－ｊ!
Ｆ（ｓ）ｅｓｔｄｓ］ε（ｔ）
１．部分分式展开法（Ｆ（ｓ）为有理函数）
２．留数法（围线积分法）
—１３—
管致中《信号与线性系统》考点精讲
１．部分分式展开法
Ｆ（ｓ）＝Ｎ（ｓ）Ｄ（ｓ）＝
ｂｍｓ
ｍ ＋ｂｍ－１ｓ
ｍ－１＋… ＋ｂ１ｓ＋ｂ０
ｓｎ＋ａｎ－１ｓ
ｎ－１＋… ＋ａ１ｓ＋ａ０
ｍｎ：Ｆ（ｓ）表示为多项式与真分式之和　（长除法）
ｍ＜ｎ：Ｆ（ｓ）为真分式，直接用该方法。
例　长除法Ｆ（ｓ）＝３ｓ
３＋２ｓ２－４ｓ＋２
ｓ２＋２ｓ＋２
多项式：其原函数为冲激函数及其各阶导数之和。
（１）ｍ＜ｎ，Ｄ（ｓ）＝０的根无重根情况
Ｆ（ｓ）＝
Ｋ１
ｓ－ｓ１
＋… ＋
Ｋｉ
ｓ－ｓｉ
＋···＋
Ｋｎ
ｓ－ｓｎ
＝∑
ｎ
ｉ＝１
Ｋｉ
ｓ－ｓｉ
Ｋｉ＝（ｓ－ｓｉ）Ｆ（ｓ）ｓ＝ｓｉ
ｆ（ｔ）＝∑
ｎ
ｉ＝１
Ｋｉｅ
ｓｉｔε（ｔ）
例１　求Ｆ（ｓ）＝ ｓ＋４
ｓ３＋３ｓ２＋２ｓ
的原函数ｆ（ｔ）
例２　求Ｆ（ｓ）＝ ｓ
ｓ２＋２ｓ＋５
的原函数ｆ（ｔ）
例３　求Ｆ（ｓ）＝ ２
（ｓ＋１）（ｓ２＋１）
的原函数ｆ（ｔ）
练　求Ｆ（ｓ）＝ ｓ＋１０
ｓ２＋１０ｓ＋５０
的原函数ｆ（ｔ）
（２）ｍ＜ｎ，Ｄ（ｓ）＝０的根有重根的情况设Ｄ（ｓ）＝０有ｐ阶重根Ｓ１
Ｆ（ｓ）＝Ｎ（ｓ）Ｄ（ｓ）＝
Ｎ（ｓ）
（ｓ－ｓ１）
ｐ ＝
Ｋ１ｐ
（ｓ－ｓ１）
ｐ＋
Ｋ１（ｐ－１）
（ｓ－ｓ１）
ｐ－１＋… ＋
Ｋ１ｋ
（ｓ－ｓ１）
ｋ＋… ＋
Ｋ１１
（ｓ－ｓ１）
其中Ｋ１ｋ ＝
１
（ｐ－ｋ）！
ｄｐ－ｋ
ｄｓｐ－ｋ
［（ｓ－ｓ１）
ｐＦ（ｓ）］
ｓ＝ｓ１
Ｋ１ｋ
（ｓ－ｓ１）
ｋ
Ｋ１ｋ
（ｋ－１）！ｔ
ｋ－１ｅｓ１ｔε（ｔ）
特例：ｐ＝２
Ｋ１２ ＝（ｓ－ｓ１）
２Ｆ（ｓ）ｓ＝ｓ１
　　Ｋ１１ ＝
ｄ
ｄｓ［（ｓ－ｓ１）
２Ｆ（ｓ）］ ｓ＝ｓ１
例　求Ｆ（ｓ）＝ １
ｓ（ｓ－１）２
的原函数ｆ（ｔ）
—２３—
２．留数法（围线积分法）———真分式
ｆ（ｔ）＝ １２πｊ∫
σ＋ｊ!
σ－ｊ!
Ｆ（ｓ）ｅｓｔｄｓ
当 ｓ＝Ｒ→ !
？，Ｆ（ｓ）→０
ｆ（ｔ）＝ １２πｊ∮ｃＦ（ｓ）ｅｓｔｄｓ＝∑
ｎ
ｉ＝１
Ｒｅｓｉ
左边的积分：Ｓ平面内沿一不通过被积函数极点的封闭曲线Ｃ进行
等式右边：围线Ｃ{
中被积函数各极点上留数之和
ｔ＞０时　ｆ（ｔ）＝ １２πｊ∫
σ＋ｊ!
σ－ｊ!
Ｆ（ｓ）ｅｓｔｄｓ＝∑
ｎ
ｉ＝１
Ｒｅｓｉ
ｔ＜０时　ｆ（ｔ）＝
{
０
∴ｆ（ｔ）＝∑
ｎ
ｉ＝１
Ｒｅｓｉε（ｔ）
（１）Ｆ（ｓ）为有理函数，在ｓ＝ｓｋ为一阶极点时，其留数为：
Ｒｅｓｋ ＝［（ｓ－ｓｋ）Ｆ（ｓ）ｅ
ｓｔ］ｓ＝ｓｋ
（２）Ｆ（ｓ）为有理函数，在ｓ＝ｓｋ为ｐ阶极点时，其留数为：
Ｒｅｓｋ ＝
１
（ｐ－１）！［
ｄｐ－１
ｄｓｐ－１
（ｓ－ｓｋ）
ｐＦ（ｓ）ｅｓｔ］
ｓ＝ｓｋ
例　（１）Ｆ（ｓ）＝ ２４（ｓ＋８）
ｓ（ｓ＋１２）（ｓ＋４）
（２）Ｆ（ｓ）＝ ４ｓ
２＋１７ｓ＋１６
（ｓ＋２）２（ｓ＋３）
结合拉普拉斯变换的基本性质求反变换。
例１　求（１－ｅ
－ｓ
ｓ ）
２
的拉普拉斯反变换
例２　求下列函数的拉普拉斯反变换
（１）１＋ｅ
－ｓ
ｓ＋１
（２） １
１＋ｅ－ｓ
（３）（１－ｅ
－ｓ
ｓ ）
２
—３３—
管致中《信号与线性系统》考点精讲
·ｍ＝２ｆ（ｋ－２）ε（ｋ）ｚ－２Ｆ（ｚ）＋ｚ－１ｆ（－１）＋ｆ（－２）
例１　ｙ（ｋ）－ｙ（ｋ－１）－２ｙ（ｋ－２）＝ｆ（ｋ）＋２ｆ（ｋ－２）ｋ０，已知ｙ（－１）＝２ｙ（－２）＝－１２ｆ（ｋ）
＝ε（ｋ），求ｙｚｉ（ｋ）ｙｚｓ（ｋ）及ｙ（ｋ）。
例２　２ｙ（ｋ＋２）＋３ｙ（ｋ＋１）＋ｙ（ｋ）＝ｆ（ｋ），已知ｙ（０）＝０，ｙ（１）＝－１，ｆ（ｋ）＝（０．５）ｋε（ｋ）
求ｙｚｉ（ｋ），ｙｚｓ及ｙ（ｋ）。
注意：初始条件（二阶系统）
后向差分方程：ｙ（－１），ｙ（－２）
前向差分方程：ｙ（０），ｙ（１）
练习　ｙ（ｋ）＋３ｙ（ｋ－１）＋２ｙ（ｋ－２）＝ｆ（ｋ）－ｆ（ｋ－１），ｙ（０）＝１，ｙ（１）＝１
ｆ（ｋ）＝ε（ｋ）。求ｙｚｉ（ｋ），ｙｚｓ（ｋ）及ｙ（ｋ）。
２．系统的零状态响应．
３．系统函数Ｈ（ｚ）
（１）定义Ｈ（ｚ）＝
Ｙｚｓ（ｚ）
Ｆ（ｚ）
（２）系统函数的零点和极点
Ｈ（ｚ）＝
ｂｍｚ
ｍ ＋ｂｍ－１ｚ
ｍ－１＋… ＋ｂ１ｚ＋ｂ０
ａｎｚ
ｎ＋ａｎ－１ｚ
ｎ－１＋… ＋ａ１ｚ＋ａ０
＝Ｈ０
（ｚ－ｚ１）…（ｚ－ｚｍ）
（ｚ－ｐ１）…（ｚ－ｐｎ）
＝Ｈ０
∏
ｍ
ｉ＝１
（ｚ－ｚｉ）
∏
ｎ
ｊ＝１
（ｚ－ｐｉ）
其中：ｚｉ：系统函数的零点　　ｐｊ：系统函数的极点
（３）系统函数的求法
① 对零状态系统的差分方程做ｚ变换即可求得Ｈ（ｚ）
例１　ｙ（ｋ）＋４ｙ（ｋ－１）＋４ｙ（ｋ－２）＝ｆ（ｋ）＋２ｆ（ｋ－１）求Ｈ（ｚ）
例２　２ｙ（ｋ＋２）＋３ｙ（ｋ＋１）＋ｙ（ｋ）＝２ｆ（ｋ＋１）求Ｈ（ｚ）
② 根据Ｈ（ｚ）的零极点及附加条件求Ｈ（ｚ）
例　已知Ｈ（ｚ）的零点为０，－２±ｊ１，极点在 －３，－１±ｊ３且Ｈ（－２）＝－１求Ｈ（ｚ）
③ 由系统的ｚ域模拟图求Ｈ（ｚ）
④ 有信号流图根据梅森公式求Ｈ（ｚ），即Ｈ＝１Δ∑ｉ ＰｉΔｉ
—０６—
（４）系统函数的应用
① 求ｈ（ｋ）：　　ｈ（ｋ）Ｈ（ｚ）
② 求ｙｚｓ（ｋ）：　　ｙｚｓ（ｋ）Ｈ（ｚ）·Ｆ（ｚ）
例　 若ｆ１（ｋ）＝ε（ｋ）－ε（ｋ－２）则ｙｚｓｉ（ｋ）＝２ε（ｋ），求ｆ２（ｋ）＝ε（ｋ）时ｙｚｓ２（ｋ）＝？
③ 由Ｈ（ｚ）写系统的差分方程，也可画模拟图及信号流图。
例　一ＬＴＩ离散系统，已知当ｙ（－１）＝０，ｙ（－２）＝１２，ｆ（－２）＝
１
２　ｆ（ｋ）＝ε（ｋ）时ｙ（ｋ）＝
［１－（－１）ｋ－（－２）ｋ］ε（ｋ），求该系统的差分方程。
④ 由Ｈ（ｚ）的极点分布判断系统的稳定性
例　已知Ｈ（ｚ）＝ ３ｚ＋１
ｚ２＋２ｚ＋２
，写出该系统的差分方程。
４．系统的频率响应
Ｈ（ｅｊω）＝Ｈ（ｚ）ｚ＝ｅｊω　 （ＤＴＦＴ）
（１）系统各队复正弦序列的稳态响应
当ｆ（ｋ）＝ｅｊωｋ时
ｙｚｓ（ｋ）＝ｆ（ｋ）ｈ（ｋ）＝∑ｈ（ｉ）ｅｊω（ｋ－ｉ）
＝ｅｊωｋ∑
!
ｉ＝－
!
ｈ（ｉ）ｅ（ｊω）－ｉ＝ｅｊωｋＨ（ｅｊω）
Ｈ（ｅｊω）＝ Ｈ（ｅｊω）ｅｊφ（ω）
∴ｙｚｓ（ｋ）＝ Ｈ（ｊω）ｅｊ［ωｋ＋φ（ω）］
结论：系统对复正弦序列的稳态响应仍是同频率的离散指数复正弦序列。
（２）系统各队正弦序列的稳态响应
当ｆ（ｋ）＝Ａｃｏｓ（ωｋ＋φ０）
ｙｚｓ（ｋ）＝ＡＨ（ｅｊω）ｃｏｓ［ωｋ＋φ０＋φ（ω）］
例１　已知ｙ（ｋ）＋２ｙ（ｋ－１）＋３ｙ（ｋ－２）＝ｆ（ｋ－１），求频率响应。
５．系统的ｚ域框图
时域模型 频域模型
数乘器 ｆ（ｋ） →
ａ
ａｆ（ｋ） Ｆ（ｚ） →
ａ
ａＦ（ｚ）
加法器
延时单元
延时单元
（零状态）
—１６—
管致中《信号与线性系统》考点精讲
例１　
已知ｆ（ｋ）＝ε（ｋ），ｙ（－１）＝０，ｙ（－２）＝１２求ｈ（ｋ），ｙｚｓ（ｋ），ｙｚｉ（ｋ）。
例２　若ｆ（ｋ）＝２＋３ｃｏｓ（０．５πｋ＋３０°）＋４ｃｏｓ（πｋ＋６０°），求系统的稳态响应ｙ（ｋ）。
例３　ｙ（ｋ）＋０．２ｙ（ｋ－１）－０．２４ｙ（ｋ－２）＝ｆ（ｋ）＋ｆ（ｋ－１）
（１）求ｈ（ｋ）　
（２）判断系统的稳定性　
（３）ｆ（ｋ）＝１２ｃｏｓ（２π），求稳态响应。
练习　ｆ（ｋ）＝５＋５ｃｏｓπ２ｋ，求稳态响应。
６．信号流图及系统模拟
（１）信号流图
常用术语，简化规则，梅森公式等在第五章已讲到。
梅森公式：Ｈ＝１
Δ∑
ｎ
ｉ＝１
ＰｉΔｉ
例１　
—２６—
求Ｈ（ｚ）
例２　已知ｎ（ｋ）＝（０．５ｋ－０．４ｋ）ε（ｋ），求该系统的信号流图。
（２）系统模拟
１°直接模拟　２°并联模拟　３°级联模拟
例１　ｙ（ｋ）－３４ｙ（ｋ－１）＋
１
８ｙ（ｋ－２）＝ｆ（ｋ）＋
１
３ｆ（ｋ－１）
７．离散系统的稳定性
（１）系统的因果性
时域：■ 若ｆ（ｋ）＜０则ｙｚｓ（ｋ）＝０，ｋ＜０
■ｈ（ｋ）＝０，ｋ＜０
■（响应不出现ｚ的正幂）
Ｚ域：■Ｈ（ｚ）的收敛区必在某圆外
■Ｈ（ｚ）＝
ｂｍｚ
ｍ ＋… ＋ｂ１ｚ＋ｂ０
ａｎｚ
ｎ＋… ＋ａ１ｚ＋ａ０
中必须ｍ
"
ｎ
（２）系统的稳定性
离散系统的判稳准则：Ｈ（ｚ）的极点全部位于单位圆内。系统稳定
朱里准则Ｈ（ｚ）＝Ｎ（ｚ）Ｄ（ｚ）
设特征多项式Ｄ（ｚ）＝ａｎｚ
ｎ＋ａｎ－１ｚ
ｎ－１＋… ＋ａ１ｚ＋ａ０
列表
行
１ ａｎ ａｎ－１ ａｎ－２ … ａ２ ａ１ ａ０
２ ａ０ ａ１ ａ２ … ａｎ－２ ａｎ－１ ａｎ
３ ｃｎ－１ ｃｎ－２ ｃｎ－３ … ｃ１ ｃ０
４ ｃ０ ｃ１ ｃ２ … ｃｎ－２ ｃｎ－１
５ ｄｎ－２ ｄｎ－３ ｄｎ－４ … ｄ０
６ ｄ０ ｄ１ ｄ２ … ｄｎ－２

２ｎ－３ ｒ２ ｒ１ ｒ０
—３６—
管致中《信号与线性系统》考点精讲
ｃｎ－１ ＝
ａｎ ａ０
ａ０ ａｎ
ｃｎ－２ ＝
ａｎ ａ１
ａ０ ａｎ－１
ｃｎ－３ ＝
ａｎ ａ２
ａ０ ａｎ－２
ｄｎ－２ ＝
ｃｎ－１ ｃ０
ｃ０ ｃｎ－１
ｄｎ－３ ＝
ｃｎ－１ ｃ１
ｃ０ ｃｎ－２
直到２ｎ－３行
朱里准则：Ｄ（ｚ）＝０的所有根都在单位圆内的充要条件是
Ｄ（１）＞０
（－１）ｎＤ（－１）＞０
ａｎ ＞ ａ０
ｃｎ－１ ＞ ｃ０
ｄｎ－１ ＞ ｄ０

ｒ２ ＞ ｒ















０
各奇数行的第一个元素比大于最后一个元素的绝对值
例１　若Ｈ（ｚ）＝ ５ｚ２＋３ｚ＋２
４ｚ４－４ｚ３＋２ｚ－１
，判断该系统是否稳定。
例２　Ｈ（ｚ）＝ ｚ２－１
ｚ２＋０．５ｚ＋（ｋ＋１）
，为使系统稳定，Ｋ应满足什么条件？
时域：∑
!
ｋ＝－
!
ｈ（ｋ）"
Ｍ（Ｍ为正常数）
ｚ域：Ｈ（ｚ）的极点必须全部在单位圆内 （朱里准则）
（单位圆上有单极点，则为边界稳定）
例　已知ｈ（ｋ）＝２ε（ｋ），则系统是 系统
Ａ．因果，稳定　　　　　　Ｂ．非因果，稳定
Ｃ．因果，非稳定 Ｄ．非因果，非稳定
六、ｓ域与ｚ域的关系
Ｓ平面与ｚ平面的映射类系
在Ｓ平面中的极点：Ｓ＝σ＋ｊω
在ｚ平面中的极点：ｚ＝ｅｓＴ ＝ｅσＴ·ρｊωＴ ＝ρｅｊθ
—４６—
其中ρ＝ｅσＴ，θ＝ωＴ
讨论：
①σ＜０：Ｓ左半平面；ρ＝ ｚ＜１即ｚ平面的单位圆内
②σ＞０：Ｓ右半平面；ρ＝ ｚ＞１即ｚ平面的单位圆外
③σ＝０：Ｓ平面虚轴；ρ＝ ｚ＝１即ｚ平面的单位圆上
—５６—
管致中《信号与线性系统》考点精讲
第九章　线性系统的状态变量分析
【本章知识要点】
一、状态方程和输出方程
二、状态方程的建立
三、状态方程的解
一、状态方程和输出方程
１．描述系统的两种方法：
■输入一输出描述法：
只关心输入信号与输出信号之间的关系，不涉及系统内部。
■状态变量描述法：
以系统内部某些变量作为状态变量，表达出系统的全部
状态和性能。
２．状态
表示动态系统的一组最少变量，只要知道ｔ＝ｔ０时这组变量和
ｔ＞ｔ０时的输入，就能完全确定系统在任何时间ｔｔ０的行为。
３．状态变量
能够表示系统状态的那些变量，ｉＬ（ｔ），ｕｃ（ｔ）等。
４．状态方程
体现系统的状态与输入之间关系的ｎ元一阶
微分／差分方程组。
５．输出方程
由状态变量和激励表示的输出响应。
二、状态方程的建立
１．连续系统状态方程的建立
ｘ
·
（ｔ）＝Ａｘ（ｔ）＋Ｂｅ（ｔ）　　 状态方程
ｙ（ｔ）＝Ｃｘ（ｔ）＋Ｄｅ（ｔ）　　 输出方程
—６６—
（１）由电路图求状态方程
■选择状态变量：ｕｃ（ｔ），ｉＬ（ｔ）
■对电容列ＫＡＬ方程，对电感列ＫＣＬ方程
■消去非状态变量
■写成标准形式
例：以ｘ３（ｔ）为输出，列写状态方程
（２）由信号流图或框图求状态方程
例１　Ｈ（ｓ）＝
ｂ３ｓ
３＋ｂ２ｓ
２＋ｂ１ｓ＋ｂ０
ｓ３＋ａ２ｓ
２＋ａ１ｓ＋ａ０
例２　
（３）由微分方程求状态方程
求解思路：微分方程→Ｈ（ｓ）→状态方程
例　ｙ″（ｔ）＋３ｙ′（ｔ）＋２ｙ（ｔ）＝５ｅ＇（ｔ）＋２ｅ（ｔ）
２．离散系统状态方程的建立
ｘ（ｋ＋１）＝Ａｘ（ｋ）＋Ｂｅ（ｋ）　状态方程
ｙ（ｋ）＝Ｃｘ（ｋ）＋Ｄｅ（ｋ）　　 输出方程
列写过程与连续系统相似
—７６—
管致中《信号与线性系统》考点精讲
　　例１　
例２　
例　ｙ（ｋ＋２）＋３ｙ（ｋ＋１）＋２ｙ（ｋ）＝ｅ（ｋ＋１）＋ｅ（ｋ）
三、状态方程的解
１．连续系统的拉普拉斯变换解
（１）ｘ
·
（ｔ）＝Ａｘ（ｔ）＋Ｂｅ（ｔ）
ｓＸ（ｓ）－ｘ（０）＝Ａｘ（ｓ）＋ＢＥ（ｓ）
（ｓＩ－Ａ）Ｘ（ｓ）＝ｘ（０）＋ＢＥ（ｓ）
Ｘ（ｓ）＝（ｓＩ－Ａ）－１ｘ（０）＋（ｓＩ－Ａ）－１ＢＥ（ｓ）
（２）ｙ（ｔ）＝Ｃｘ（ｔ）＋Ｄｅ（ｔ）
Ｙ（ｓ）＝ＣＸ（ｓ）＋ＤＥ（ｓ）
＝Ｃ（ｓＩ－Ａ）－１ｘ（０）＋［Ｃ（ｓＩ－Ａ）－１Ｂ＋Ｄ］Ｅ（ｓ）
＝Ｙｚｉ（ｓ）＋Ｙｚｓ（ｓ）
（３）预解矩阵　　　　　　Φ（ｓ）＝（ｓＩ－Ａ）－１
状态转移矩阵φ（ｔ）＝ｅＡｔΦ（ｓ）＝（ｓＩ－Ａ）－１
系统函数矩阵　　Ｈ（ｓ）＝ＣΦ（ｓ）Ｂ＋Ｄ
冲激响应矩阵ｈ（ｔ）＝Ｃφ（ｔ）Ｂ＋Ｄδ（ｔ）
—８６—
考试点（ｗｗｗ．ｋａｏｓｈｉｄｉａｎ．ｃｏｍ）名师精品课程　电话：４００６８８５３６５
（４）判稳
Ｄ（ｓ）＝ｄｅｔ（ｓＩ－Ａ）＝０的根全部位于ｓ的左半平面，则系统稳定。
例　
２．离散系统的Ｚ变换解
（１）ｘ（ｋ＋１）＝Ａｘ（ｋ）＋Ｂｅ（ｋ）
ｚｘ（ｚ）－ｚｘ（０）＝ＡＸ（ｚ）＋ＢＥ（ｚ）
Ｘ（ｚ）＝（ｚＩ－Ａ）－１ｚｘ（０）＋（ｚＩ－Ａ）－１ＢＥ（ｚ）
（２）ｙ（ｋ）＝Ｃｘ（ｋ）＋Ｄｅ（ｋ）
Ｙ（ｚ）＝Ｃｘ（ｚ）＋ＤＥ（ｚ）＝Ｃ（ｚＩ－Ａ）－１ｚｘ（０）＋［Ｃ（ｚＩ－Ａ）－１Ｂ＋Ｄ］Ｅ（ｚ）
（３）预解矩 　　　Φ（ｚ）＝（ｚＩ－Ａ）－１ｚ
状态转移矩阵　φ（ｋ）＝ＡｋΦ（ｚ）
系统函数矩阵　　Ｈ（ｚ）＝ＣΦ（ｚ）ｚ－１Ｂ＋Ｄ
冲激响应矩阵ｈ（ｋ）Ｈ（ｚ）
（４）判稳
Ｄ（ｚ）＝ｄｅｔ（ｚＩ－Ａ）＝０的根全部位于单位圆内，则系统稳定。
—９６—
管致中《信号与线性系统》考点精讲
阵