概要信息：

第１章　绪论 （１）
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
第２章　确知信号 （９）
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
第３章　随机过程 （１６）
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
第４章　信道 （２４）
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
第５章　模拟通信系统 （３０）
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
第６章　数字基带传输系统 （４４）
!!!!!!!!!!!!!!!!!!!!!!!!!!!!
第７章　数字带通传输系统 （５３）
!!!!!!!!!!!!!!!!!!!!!!!!!!!!
第８章　新型数字通带调制技术 （６３）
!!!!!!!!!!!!!!!!!!!!!!!!!!
第９章　模拟信号的数字化传输 （６７）
!!!!!!!!!!!!!!!!!!!!!!!!!!
第１０章　数字信号的最佳接收 （７５）
!!!!!!!!!!!!!!!!!!!!!!!!!!
樊昌信《通信原理》考研考点精讲
１　
? 第一章
绪　论
１．通信中常用的术语
（１）通信：利用电或光信号将消息中所包含的信息从信源发送到一个或多个目的地。因此，通信
的目的是传递消息中所包含的信息。
（２）消息：信息的物理表现形式，即语音、图像、符号、数字、图片等具有概率论意义上的“事件”。
消息带有需要送给收信者的信息，并以信号的形式在系统中进行传输。
（３）信息：消息中包含的有意义内容，即包含受信者原来不知而待知的有效内容。
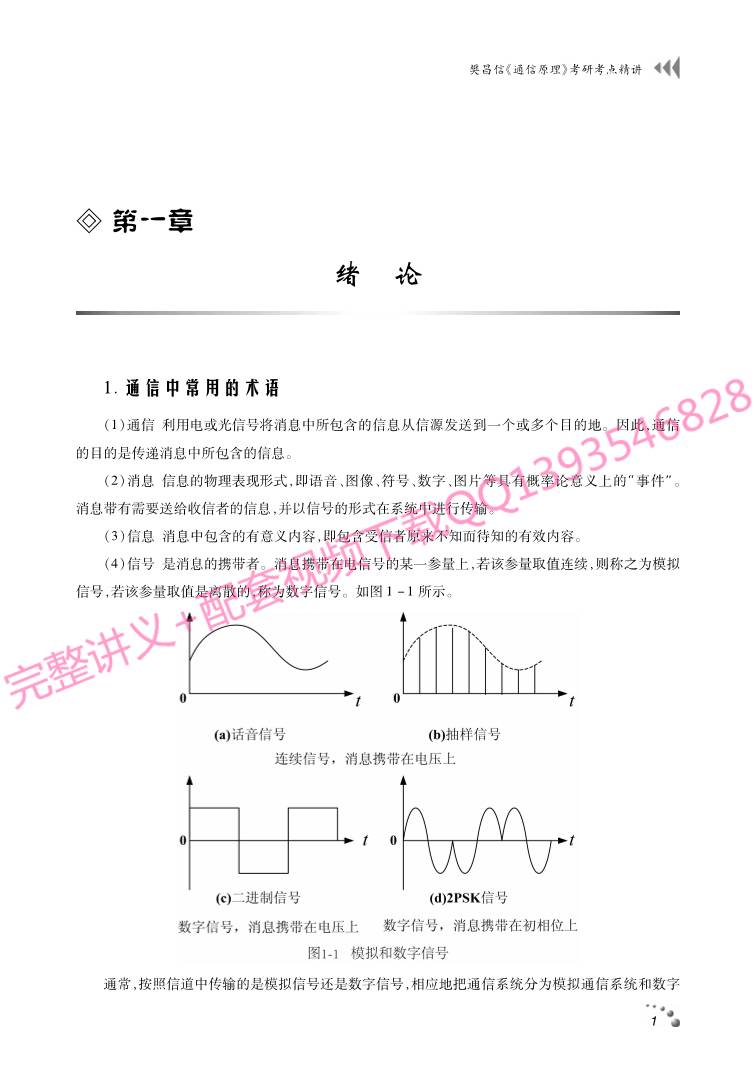
（４）信号：是消息的携带者。消息携带在电信号的某一参量上，若该参量取值连续，则称之为模拟
信号，若该参量取值是离散的，称为数字信号。如图１－１所示。
通常，按照信道中传输的是模拟信号还是数字信号，相应地把通信系统分为模拟通信系统和数字
２　
通信系统。
２．通信系统的组成
通信系统是指传递消息所需要的一切技术设备（包括信道）的总和。
２．１．通信系统一般模型
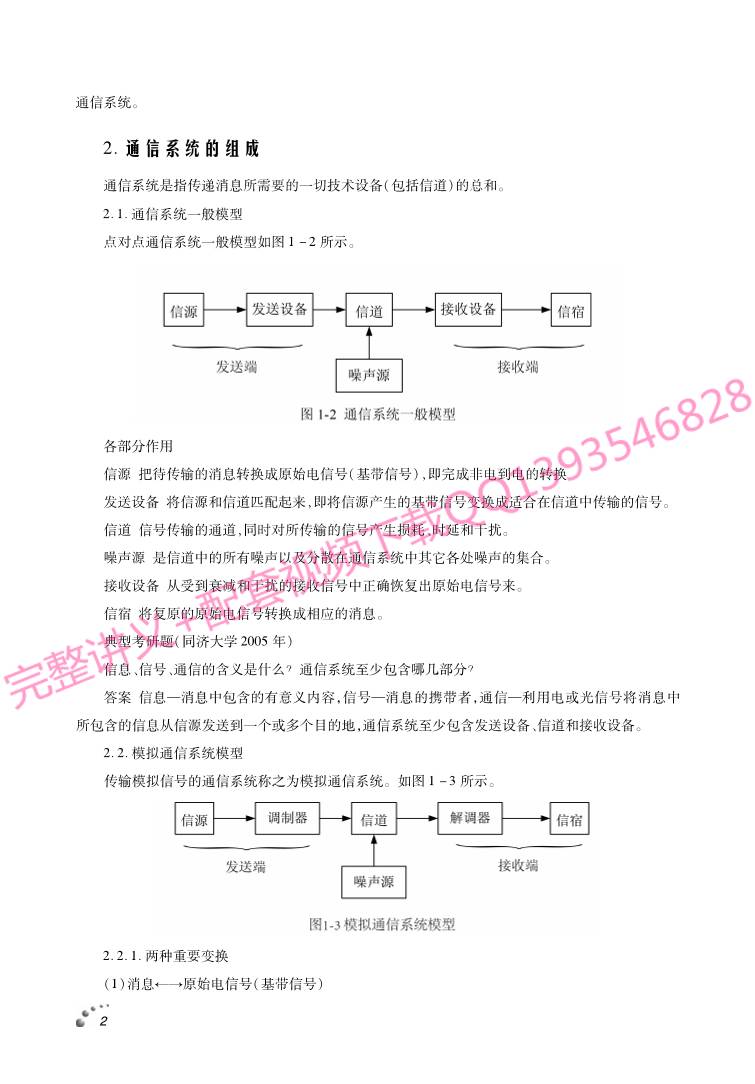
点对点通信系统一般模型如图１－２所示。
各部分作用：
信源：把待传输的消息转换成原始电信号（基带信号），即完成非电到电的转换
发送设备：将信源和信道匹配起来，即将信源产生的基带信号变换成适合在信道中传输的信号。
信道：信号传输的通道，同时对所传输的信号产生损耗、时延和干扰。
噪声源：是信道中的所有噪声以及分散在通信系统中其它各处噪声的集合。
接收设备：从受到衰减和干扰的接收信号中正确恢复出原始电信号来。
信宿：将复原的原始电信号转换成相应的消息。
典型考研题（同济大学２００５年）
信息、信号、通信的含义是什么？通信系统至少包含哪几部分？
答案：信息—消息中包含的有意义内容；信号—消息的携带者；通信—利用电或光信号将消息中
所包含的信息从信源发送到一个或多个目的地；通信系统至少包含发送设备、信道和接收设备。
２．２．模拟通信系统模型
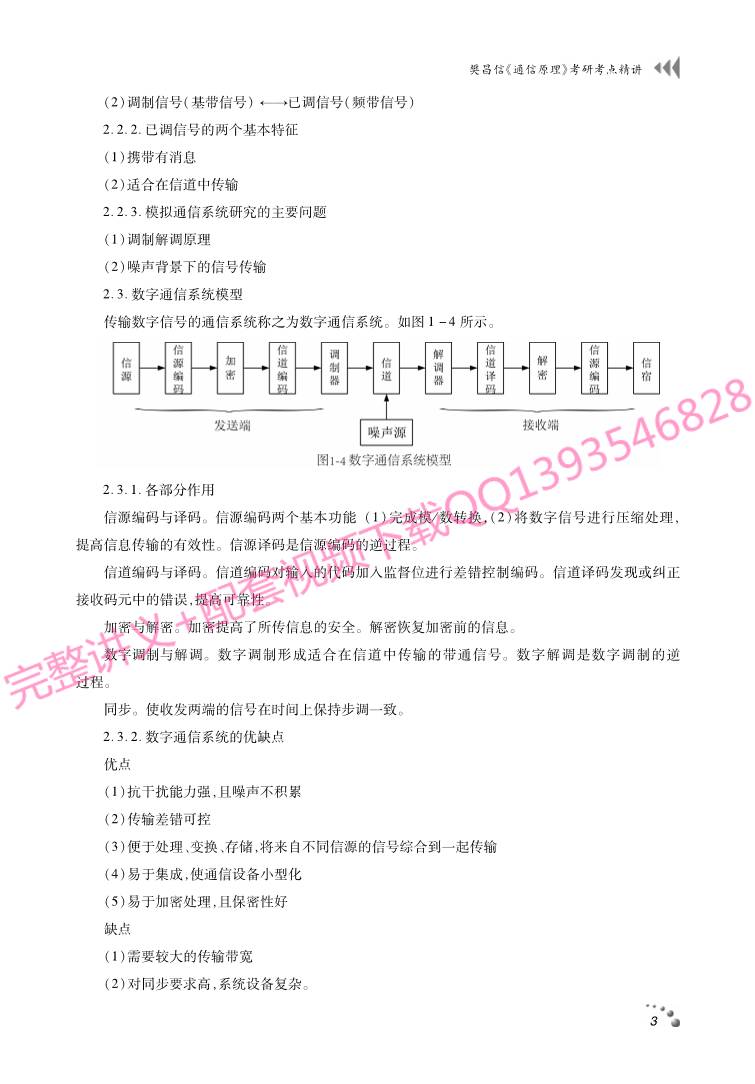
传输模拟信号的通信系统称之为模拟通信系统。如图１－３所示。
２．２．１．两种重要变换
（１）消息←→原始电信号（基带信号）
樊昌信《通信原理》考研考点精讲
３　
（２）调制信号（基带信号）←→已调信号（频带信号）
２．２．２．已调信号的两个基本特征
（１）携带有消息
（２）适合在信道中传输
２．２．３．模拟通信系统研究的主要问题
（１）调制解调原理
（２）噪声背景下的信号传输
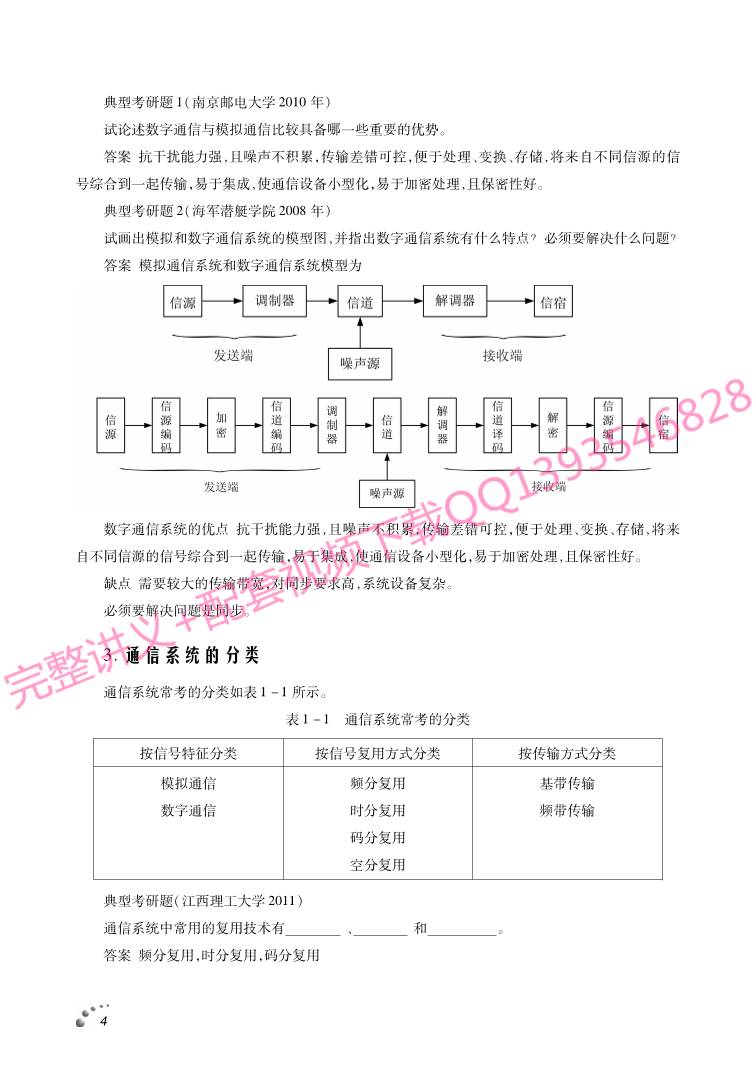
２．３．数字通信系统模型
传输数字信号的通信系统称之为数字通信系统。如图１－４所示。
２．３．１．各部分作用
信源编码与译码。信源编码两个基本功能：（１）完成模／数转换；（２）将数字信号进行压缩处理，
提高信息传输的有效性。信源译码是信源编码的逆过程。
信道编码与译码。信道编码对输入的代码加入监督位进行差错控制编码。信道译码发现或纠正
接收码元中的错误，提高可靠性。
加密与解密。加密提高了所传信息的安全。解密恢复加密前的信息。
数字调制与解调。数字调制形成适合在信道中传输的带通信号。数字解调是数字调制的逆
过程。
同步。使收发两端的信号在时间上保持步调一致。
２．３．２．数字通信系统的优缺点
优点：
（１）抗干扰能力强，且噪声不积累
（２）传输差错可控
（３）便于处理、变换、存储，将来自不同信源的信号综合到一起传输
（４）易于集成，使通信设备小型化
（５）易于加密处理，且保密性好
缺点：
（１）需要较大的传输带宽
（２）对同步要求高，系统设备复杂。
４　
典型考研题１（南京邮电大学２０１０年）
试论述数字通信与模拟通信比较具备哪一些重要的优势。
答案：抗干扰能力强，且噪声不积累；传输差错可控；便于处理、变换、存储，将来自不同信源的信
号综合到一起传输；易于集成，使通信设备小型化；易于加密处理，且保密性好。
典型考研题２（海军潜艇学院２００８年）
试画出模拟和数字通信系统的模型图，并指出数字通信系统有什么特点？必须要解决什么问题？
答案：模拟通信系统和数字通信系统模型为
数字通信系统的优点：抗干扰能力强，且噪声不积累；传输差错可控；便于处理、变换、存储，将来
自不同信源的信号综合到一起传输；易于集成，使通信设备小型化；易于加密处理，且保密性好。
缺点：需要较大的传输带宽；对同步要求高，系统设备复杂。
必须要解决问题是同步。
３．通信系统的分类
通信系统常考的分类如表１－１所示。
表１－１　通信系统常考的分类
按信号特征分类 按信号复用方式分类 按传输方式分类
模拟通信
数字通信
频分复用
时分复用
码分复用
空分复用
基带传输
频带传输
　　典型考研题（江西理工大学２０１１）
通信系统中常用的复用技术有　　　　 、　　　　 和　　　　　。
答案：频分复用；时分复用；码分复用
樊昌信《通信原理》考研考点精讲
５　
４．通信方式
通信系统常考的通信方式如表１－２、１－３所示。
表１－２　按消息传递方向和时间分类的通信方式
按消息传递
方向和时间
定义 典型例子
单工通信 消息只能单方向传递 广播、无线寻呼
半双工通信 通信双方都能收或发消息，但不能同时进行收发 使用同一载频的普通对讲机
全双工通信 通信双方可同时收发消息 电话通信
表１－３　按数据代码排列时序分类的通信方式
按数据代码排列时序 定义 优缺点
并行传输
将代表消息的数字码元序列
以成组的方式在两条或两条
以上的并行信道上同时传输
优点：节省传输时间，速度快，不需要字
符同步措施；缺点：需要多条通信线路，
成本高，不适合远距离通信
串行传输
将代表消息的数字码元序列
以串行方式一个码元接一个
码元在一条信道上传输
优点：只需一条通信信道，节省线路铺设
费用，适合远距离传输；缺点：速度慢，需
要外加码组或字符同步措施
５．信息及其度量
５．１关于信息的几点讨论
（１）消息中所包含的信息量与消息发生的概率密切相关，而与消息的种类和重要程度无关。
（２）不同形式的消息可以包含相同的信息。
（３）消息出现的概率越小，所包含的信息量就越大，消息出现的概率越大，所包含的信息量就越
小，当消息出现的概率为１时，信息量为０。
（４）若干个互相独立事件构成的消息，所含信息量等于各独立事件信息量之和。
５．２离散消息的信息量
Ｉ＝ｌｏｇ２
１
Ｐ（ｘ）＝－ｌｏｇ２Ｐ（ｘ）（比特）
５．３离散信源的平均信息量
对于Ｍ进制的离散信源，设各符号出现的概率为
ｘ１， ｘ２，…，ｘＭ
Ｐ（ｘ１），Ｐ（ｘ２），…，Ｐ（ｘＭ





）
６　
注意
∑
Ｍ
ｉ＝１
Ｐ（ｘｉ）＝１
Ｍ进制的离散信源的平均信息量
Ｈ( )ｘ＝－Ｐ（ｘ１）ｌｏｇ２Ｐ（ｘ１）－Ｐ（ｘ２）ｌｏｇ２Ｐ（ｘ２）… －Ｐ（ｘＭ）ｌｏｇ２Ｐ（ｘＭ）
＝－∑
Ｍ
ｉ＝１
Ｐ（ｘｉ）ｌｏｇ２Ｐ（ｘｉ）（比特／符号）
注意，Ｍ进制的离散信源各符号独立等概出现时，即
Ｐ（ｘｉ）＝
１
Ｍ， ｉ＝１，２，…，Ｍ
平均信息量即信息熵最大
Ｈｍａｘ＝ｌｏｇ２Ｍ（比特／符号）
５．４总信息量
Ｉ＝ｍ·Ｈ( )ｘ（比特）
其中，ｍ是总的符号数。
典型考研题（西安电子科技大学２０１０年）
某四进制信源，其中一个符号出现的概率是１／２，且各符号的出现是相对独立的，则要使该符号集
的平均信息量最大，其余三个符号出现的概率分别为　１／６　 。
答案：∑
４
ｉ＝１
Ｐｘ( )
ｉ ＝１，假定Ｐｘ( )
１ ＝
１
２，则平均信息量最大，要求
Ｐｘ( )
１ ＝Ｐｘ( )
２ ＝Ｐｘ( )
３ ＝
１
６
６．通信系统的主要性能指标
通信的任务是快速、准确地传递信息，从研究消息传输的角度来说，有效性和可靠性是评价通信
系统优劣的主要性能指标。
（１）有效性：传输一定信息量时所占用的信道资源（带宽或时间间隔即时隙的大小）。
（２）可靠性：接收信息的准确程度。
６．１模拟通信系统的主要性能指标
（１）有效性：传输带宽。传输同样的消息所需的带宽越小，有效性就越好。
（２）可靠性：输出信噪比。
６．２数字通信系统的主要性能指标
６．２．１有效性———传输速率和频带利用率
（１）码元传输速率ＲＢ（数码率、传码率、码率、信号速率或波形速率）　　　　
①定义：单位时间内传输码元的数目。
樊昌信《通信原理》考研考点精讲
７　
②单位：波特（Ｂａｕｄ），用符号“Ｂ”表示。
ＲＢ ＝
１
Ｔ（波特）
③时间ｔ内传输的总码元数
Ｎ＝ＲＢ·ｔ（个）
（２）信息传输速率Ｒｂ（信息速率、传信率、比特率）　　　　
①定义：单位时间内传输比特的数目。
②单位：比特／秒（ｂｉｔ／ｓ），简记为ｂ／ｓ或ｂｐｓ。
③传码率与传信率之间的关系
Ｒｂ ＝ＲＢ·Ｈ( )ｘ（比特／秒）
④等概条件下，Ｍ进制信源传信率与传码率的关系
Ｒｂ ＝ＲＢ·ｌｏｇ２Ｍ（比特／秒）
讨论：
ｉ　Ｒｂ不变，用多进制传输可以降低传码率，从而减小信号带宽，提高频带利用率（ｂｉｔ／（ｓ!
Ｈｚ））。
ｉ　ＲＢ不变（即所需信道带宽不变），用多进制传输可以增加传信率，从而在相同的带宽中传输更
多的信息量。
当Ｍ ＝２时，传信率和传码率在数值上相等，即
Ｒｂ ＝ＲＢ
⑤时间ｔ内传输的总信息量
Ｉ＝Ｒｂ·ｔ＝ＲＢｌｏｇ２Ｍ·ｔ（比特）
（３）频带利用率
①定义：单位带宽内的传输速率。
②单位：波特／赫兹（Ｂａｕｄ／Ｈｚ）或比特／（秒!
赫兹）（ｂｉｔ／（ｓ·Ｈｚ））。
η＝
ＲＢ
Ｂ（Ｂａｕｄ／Ｈｚ）
ηｂ ＝
Ｒｂ
Ｂ（ｂｉｔ／（ｓ·Ｈｚ））
独立等概时
ηｂ ＝ηｌｏｇ２Ｍ（ｂｉｔ／（ｓ!Ｈｚ））
６．２．２可靠性———差错率
（１）误码率
Ｐｅ＝
单位时间内接收的错误码元数
单位时间内系统传输的总码元数
（２）误信率
８　
Ｐｂ ＝
单位时间内接收的错误比特数
单位时间内系统传输的总比特数
（３）Ｍ进制独立等概条件下，误码率和误信率的关系
Ｐｂ≈
Ｐｅ
ｌｏｇ２Ｍ
当Ｍ ＝２时，Ｐｅ＝Ｐｂ。
典型考研题１（西南交通大学２００５年）
设一数字系统传输 １６进制码元，码元传输速率为 ２４００波特，此时系统的信息传输速率为
９６００ｂｉｔ／ｓ；如果系统的误码率为１０－４，则一小时内错误的码元个数为　８６４个　；若果系统的误比特
率为２．５×１０－５，则十分钟内错误的比特个数是　 １４４个　　　 。
答案：Ｒｂ ＝ＲＢｌｏｇ２１６＝９６００ｂｉｔ／ｓ；２４００×３６００×１０
－４＝８６４个；９６００×６００×２．５×１０－５＝１４４
个
典型考研题２（西安邮电大学２０１１）
某离散信源符号集有四个符号组成，其中，前三个符号出现的概率分别为１／４，１／８，１／８，且各符号
的出现是相对独立的，试计算：
１）该信息源的熵？
２）若信息源以１０００Ｂ的速率传输信息，此时的信息传输速率是多少？
３）在此码元速率下，该信息源的最大信息传输速率是多少？
樊昌信《通信原理》考研考点精讲
９　
? 第二章
确知信号
１．确知信号和随机信号
确知信号和随机信号如表２－１所示。
表２－１　确知信号和随机信号
名称 定义 举例
确知信号
可以预先知道其变化规律的信号，在定义域的
任意时刻都有确定的函数值
振幅、频率和相位都确定的正
弦波Ａｃｏｓωｔ＋( )φ
随机信号
不可以预先知道其变化规律的信号，在定义域
的任意时刻没有确定的函数值
高斯白噪声
２．能量信号和功率信号
能量信号和功率信号如表２－２所示。
通信中定义的连续电压或电流信号 ｓ( )ｔ在单位电阻（１欧姆）上的瞬时功率为 ｓ２( )ｔ，则信号
ｓ( )ｔ总能量和平均功率分别为
总能量　Ｅ＝∫
!
－
!
ｓ２( )ｔｄｔ（Ｊ）
平均功率　Ｐ＝ｌｉｍ
Ｔ→!
１
Ｔ∫
Ｔ／２
－Ｔ／２
ｓ２( )ｔｄｔ（Ｗ）
表２－２　能量信号和功率信号
名称 定义 特征
能量信号
０＜Ｅ＜
!
Ｐ→０
幅度和持续时间有限，非周期
功率信号
０＜Ｐ＜
!
Ｅ→ !
的函数值
持续时间无限，
直流信号、周期信号和随机信号
１０　
３．常用的傅里叶变换对
（１）门函数
常用门函数的傅里叶变换对如表２－３所示。
表２－３　常用门函数的傅里叶变换对
Ｇ( )ω ＝∫
!
－
!
ｇ( )ｔｅ－ｊ２πｆｔｄｔ
＝Ａτ·ｓａ２πｆ·τ( )２ ＝Ｇ( )ｆ
单位：伏／赫兹
ｇ( )ｔ＝∫
!
－
!
Ｇ( )ｆｅｊ２πｔｆｄｆ＝ＡＢＨ·ｓａ２πｔ·
ＢＨ( )２
ｇ( )ｔ＝
１
２π∫
!
－
!
Ｇ( )ωｅｊｔωｄω
＝ １２π
ＡωＨ·ｓａｔ·
ωＨ( )２
（２）三角函数
常用门函数的傅里叶变换对如表２－４所示。
表２－４　常用三角函数的傅里叶变换对
Ｒ( )ω ＝∫
!
－
!
ｒ( )ｔｅ－ｊ２πｆｔｄｔ
＝Ａτ·ｓａ２ ２πｆ·τ( )２ ＝Ｒ( )ｆ
单位：伏／赫兹
ｒ( )ｔ＝∫
!
－
!
Ｒ( )ｆｅｊ２πｔｆｄｆ＝ＡＢＨ·ｓａ
２ ２πｔ·
ＢＨ( )２
ｒ( )ｔ＝
１
２π∫
!
－
!
Ｒ( )ωｅｊｔωｄω
＝ １２π
ＡωＨ·ｓａ
２ ｔ·
ωＨ( )２
樊昌信《通信原理》考研考点精讲
１１　
　　（３）周期函数
常用周期函数的傅里叶变换对如表２－５所示。
表２－５　常用周期函数的傅里叶变换对
周
期
冲
激
序
列
δＴ( )ｔ＝∑
!
ｎ＝－
!
δ( )ｔ－ｎＴ ＝∑
!
ｎ＝－
!
Ｃｎｅ
ｊ２πｎｆ０ｔ ｆ０ ＝１／Ｔ
Ｃｎ ＝
１
Ｔ∫
Ｔ／２
－Ｔ／２
δＴ( )ｔｅ－ｊ２πｎｆ０ｔｄｔ＝
１
Ｔ　　表示谐波分量ｎｆ０的复振幅，单位：伏。
δＴ( )ω ＝∑
!
ｎ＝－
!
Ｃｎ２πδω－ｎω( )
０ ＝∑
!
ｎ＝－
!
Ｃｎδｆ－ｎｆ( )
０
＝１Ｔ∑
!
ｎ＝－
!
２πδω－ｎω( )
０ ＝
１
Ｔ∑
!
ｎ＝－
!
δｆ－ｎｆ( )
０ ＝δＴ( )ｆ
周
期
矩
形
序
列
ｇＴ( )ｔ＝∑
!
ｎ＝－
!
ｇ( )ｔ－ｎＴ ＝∑
!
ｎ＝－
!
Ｃｎｅ
ｊ２πｎｆ０ｔ ｆ０ ＝１／Ｔ
Ｃｎ ＝
１
Ｔ∫
Ｔ／２
－Ｔ／２
ｇＴ（ｔ）ｅ
－ｊ２πｎｆ０ｔｄｔ＝１Ｔ·Ａτ·ｓａ（２πｎｆ０·
τ
２）
表示谐波分量ｎｆ０的复振幅，单位：伏。
ＧＴ( )ω ＝∑
!
ｎ＝－
!
Ｃｎ２πδ（ω－ｎω０）＝∑
!
ｎ＝－
!
Ａτ
Ｔ·ｓａ（πｎｆ０τ）·２πδ（ω－ｎω０）
＝∑
!
ｎ＝－
!
Ａτ
Ｔ·ｓａ（πｎｆ０τ）·δ（ｆ－ｎｆ０）＝ＧＴ（ｆ）
１２　
周
期
三
角
序
列
ｒＴ( )ｔ＝∑
!
ｎ＝－
!
ｒ( )ｔ－ｎＴ ＝∑
!
ｎ＝－
!
Ｃｎｅ
ｊ２πｎｆ０ｔ ｆ０ ＝１／Ｔ
Ｃｎ ＝
１
Ｔ∫
Ｔ／２
－Ｔ／２
ｒＴ( )ｔｅ－ｊ２πｎｆ０ｔｄｔ＝
１
Ｔ·Ａτ·ｓａ
２ ２πｎｆ０·
τ( )２
表示谐波分量ｎｆ０的复振幅，单位：伏。
ＲＴ( )ω ＝∑
!
ｎ＝－
!
Ｃｎ２πδω－ｎω( )
０ ＝∑
!
ｎ＝－
!
Ａτ
Ｔ·ｓａ
２ πｎｆ０( )τ·２πδω－ｎω( )
０
＝∑
!
ｎ＝－
!
Ａτ
Ｔ·ｓａ
２ πｎｆ０( )τ·δｆ－ｎｆ( )
０ ＝ＲＴ( )ｆ
　　（４）其余函数
其余的傅里叶变换对如表２－６所示。
表２－６　其余函数的傅里叶变换对
欧
拉
公
式
ｅ±ｊωｃｔ＝ｃｏｓωｃｔ±ｊｓｉｎωｃｔ２πδωω( )
ｃ ＝δｆｆ( )
ｃ
ｃｏｓωｃｔ＝
１
２ ｅ
ｊωｃｔ＋ｅ－ｊωｃ( )ｔπ δω－ω( )
ｃ ＋δω＋ω( )[ ]
ｃ
＝１２ δｆ－ｆ( )
ｃ ＋δｆ＋ｆ( )[ ]
ｃ
ｓｉｎωｃｔ＝
１
２ｊｅ
ｊωｃｔ－ｅ－ｊωｃ( )ｔ πｊδω－ω( )
ｃ －δω＋ω( )[ ]
ｃ
＝１２ｊδｆ－ｆ( )
ｃ －δｆ＋ｆ( )[ ]
ｃ
频
移
特
性
ｍ( )ｔｅ±ｊωｃｔＭ ωω( )
ｃ
ｍ( )ｔｃｏｓωｃｔ
１
２ Ｍ ω－ω( )
ｃ ＋Ｍ ω＋ω( )[ ]
ｃ
＝１２ Ｍ ｆ－ｆ( )
ｃ ＋Ｍ ｆ＋ｆ( )[ ]
ｃ
ｍ( )ｔｓｉｎωｃｔ
１
２ｊＭ ω－ω( )
ｃ －Ｍ ω＋ω( )[ ]
ｃ
＝１２ｊＭ ｆ－ｆ( )
ｃ －Ｍ ｆ＋ｆ( )[ ]
ｃ
樊昌信《通信 理》考研考点精讲
１３　
时移
特性
ｍ ｔ±ｔ( )
ｄ Ｍ( )ωｅ±ｊωｔｄ
卷积
ｍ( )ｔδｔ±ｔ( )
ｄ ＝ｍ ｔ±ｔ( )
ｄ
Ｍ( )ωδω±ω( )
ｃ ＝Ｍ ω±ω( )
ｃ
指数 ｅ－ａ ｔ ２ａ
ａ２＋ω２
４．能量谱密度和功率谱密度
帕氏瓦尔能量和功率守恒定理如表２－７所示。
表２－７　帕氏瓦尔能量谱和功率谱守恒定理
名称 定　义 物理含义
能量
守恒
Ｅ＝∫
!
－
!
ｓ２( )ｔｄｔ＝∫
!
－
!
ｓ( )ｆ ２ｄｆ
能量信号的能量在时域和频域中保持
守恒
功率
守恒
Ｐ＝ｌｉｍ
Ｔ→!
１
Ｔ∫
Ｔ／２
－Ｔ／２
ｓ２( )ｔｄｔ＝∫
!
－
!
Ｐ( )ｆｄｆ
功率信号的功率在时域和频域中保持
守恒
周期信
号功率
Ｐ＝∑
!
ｎ＝－
!
Ｃｎ
２
＝Ｃ２０＋２∑
!
ｎ＝１
Ｃｎ
２ 周期信号的平均功率等于所包含的直
流及基波和各次谐波的平均功率之和
　　能量谱密度和功率谱密度如表２－８所示。
表２－８　能量谱密度和功率谱密度
名称 定义 物理含义
能量谱密度 Ｇ( )ｆ＝ ｓ( )ｆ ２（Ｊ／Ｈｚ）
在频率ｆ处，带宽为 ｄｆ频带内
的信号能量
非周期信号
功率谱密度
Ｐ( )ｆ＝ｌｉｍ
Ｔ→!
１
Ｔ ｓＴ( )ｆ ２（Ｗ／Ｈｚ）
在频率ｆ处，带宽为 ｄｆ频带内
的信号功率
周期信号
功率谱密度
Ｐ( )ｆ＝∑
!
ｎ＝－
!
Ｃｎ
２
δｆ－ｎｆ( )
０
第ｎ次谐波，即ｎｆ０的功率
５．自相关函数和互相关函数
自相关函数和互相关函数如表２－９所示。
１４　
表２－９　自相关函数和互相关函数
名称 定义 性质
能量信号的
自相关函数
Ｒ( )τ＝∫
!
－
!
ｓ( )ｔｓｔ＋( )τｄｔ
Ｒ( )τ＝Ｒ －( )τ
Ｒ( )τ "
Ｒ( )０
Ｒ( )０ ＝Ｅ
功率信号的
自相关函数
Ｒ( )τ＝ｌｉｍ
Ｔ→!
１
Ｔ∫
Ｔ／２
－Ｔ／２
ｓ( )ｔｓｔ＋( )τｄｔ
Ｒ( )τ＝
１
Ｔ０∫
Ｔ０／２
－Ｔ０／２
ｓ( )ｔｓｔ＋( )τｄｔ
Ｒ( )τ＝Ｒ －( )τ
Ｒ( )τ "
Ｒ( )０
Ｒ( )０ ＝Ｐ
能量信号的
互相关函数
Ｒ１２( )τ＝∫
!
－
!
ｓ１( )ｔｓ２ ｔ＋( )τｄｔ Ｒ１２( )τ＝Ｒ２１ －( )τ
功率信号的
互相关函数
Ｒ１２( )τ＝ｌｉｍ
Ｔ→!
１
Ｔ∫
Ｔ／２
－Ｔ／２
ｓ１( )ｔｓ２ ｔ＋( )τｄｔ Ｒ１２( )τ＝Ｒ２１ －( )τ
能量信号的
互相关系数
ρ１２ ＝
∫
!
－
!
ｓ１( )ｔｓ２( )ｔｄｔ
Ｅ１Ｅ槡 ２
ρ１２ "
１；ρ１２＝－１
ｓ１( )ｔ＝－ｓ２( )ｔ
ρ１２ ＝ｓ１( )ｔ与ｓ２( )ｔ正交
功率信号的
互相关系数
ρ１２ ＝
ｌｉｍ
Ｔ→!
１
Ｔ∫
Ｔ／２
－Ｔ／２
ｓ１( )ｔｓ２( )ｔｄｔ
Ｐ１Ｐ槡 ２
ρ１２ "
１；ρ１２＝－１
ｓ１( )ｔ＝－ｓ２( )ｔ
ρ１２ ＝ｓ１( )ｔ与ｓ２( )ｔ正交
６．相关函数与功率谱密度的关系
相关函数与功率谱密度的关系如表２－１０所示。
表２－１０　相关函数与功率谱密度
能量信号 Ｒ( )τ Ｓ( )ｆ ２傅里叶变换对
功率信号 Ｒ( )τＰ( )ｆ傅里叶变换对
７．双边谱与单边谱的关系
双边谱与单边谱的的关系如表２－１１所示。
樊昌信《通信原理》考研考点精讲
１５　
表２－１１　双边谱与单边谱的关系
名称 定义 物理含义
双边谱 分布在正负频率范围内的频谱或功率谱 数学上的描述方法，负频谱无实际物理意义
单边谱 分布在正频率范围内的频谱或功率谱 物理信号可测量的频谱，决定信号带宽
１６　
? 第三章
随机过程
１．随机过程的基本概念
测试ｎ台性能相同的接收机，在同样条件下，不加信号测试其输出噪声，波形如图３－１所示。
（１）每一条曲线ξｉ( )ｔ都是一个随机起伏的时间函数－－样本函数（确知信号），称之为随机过程
ξ( )ｔ的一个实现／样本。
（２）全体样本函数的集合称作随机过程ξ( )ｔ。
ξ( )ｔ＝ ξ１( )ｔ，ξ２( )ｔ，…，ξｎ( ){ }ｔ
（３）在某一特定时刻ｔ１观察各台接收机的输出噪声值ξｔ( )
１ ，是随机过程ξ( )ｔ一个随机量（随机
变量）
ξｔ( )
１ ＝ ξ１ ｔ( )
１ ，ξ２ ｔ( )
１ ，…，ξｎ ｔ( ){ }
１
因此，随机过程ξ( )ｔ是由无穷多个随机变量构成的。
ξ( )ｔ＝ ξｔ( )
１ ，ξｔ( )
２ ，…，ξｔ( )
ｎ
{ }，…
２．随机过程的数字特征
随机过程的数字特征如表３－１所示。
樊昌信《通信原理》考研考点精讲
１７　
表３－１　随机过程的数字特征
名称 定义 含义
均值
Ｅξ( )[ ]ｔ ＝∫
!
－
!
ｘｆ１ ｘ，( )ｔｄｘ＝ａ( )ｔ
ξ( )ｔ中的ｔ取任意时刻，
ξ( )ｔ对应随机变量，下同
随机过程的摆动中心
均方值 Ｅξ２( )[ ]ｔ ＝∫
!
－
!
ｘ２ｆ１ ｘ，( )ｔｄｘ 随机过程的平均功率
方差
Ｄξ( )[ ]ｔ ＝Ｅ ξ( )ｔ－ａ( )[ ]ｔ{ }２
＝Ｅξ２( )[ ]ｔ －ａ２( )ｔ＝σ２( )ｔ
随机过程的交流功率，相对于
均值的振动程度
自相关函数
Ｒｔ１，ｔ( )
２ ＝Ｅξｔ( )
１ ξｔ( )[ ]
２
＝∫
!
－
!
∫
!
－
!
ｘ１ｘ２ｆ２ ｘ１，ｘ２；ｔ１，ｔ( )
２ ｄｔ１ｄｔ２ ＝Ｒｔ１，ｔ１＋( )τ
随机过程在两个不同时刻的
随机变量之间的关联程度
协方差函数
Ｂｔ１，ｔ( )
２ ＝Ｅ ξｔ( )
１ －ａｔ( )[ ]
１ ξｔ( )
２ －ａｔ( )[ ]{ }
２
＝Ｒｔ１，ｔ( )
２ －ａｔ( )
１ ａｔ( )
２
互相关函数 Ｒξη ｔ１，ｔ( )
２ ＝Ｅξｔ( )
１ ηｔ( )[ ]
２
＝Ｒξη ｔ１，ｔ１＋( )τ
两个随机过程在两个不同时
刻的随机变量之间的关联
程度
　　典型考研题（中国科学院研究生院２０１２年）
若ｎ１，ｎ２是两个独立同分布的零均值高斯噪声，方差都是１，则ｎ１×ｎ２的方差是　１　，ｎ１＋ｎ２的
方差是　 ２　。
答案：
Ｅｎ１×ｎ[ ]
２ ＝Ｅｎ[ ]
１ Ｅｎ[ ]
２ ＝０Ｄｎ１×ｎ[ ]
２ ＝Ｅ ｎ１×ｎ２－( )０[ ]２ ＝Ｅｎ[ ]２
１ Ｅｎ[ ]２
２ ＝１
Ｅｎ１＋ｎ[ ]
２ ＝Ｅｎ[ ]
１ ＋Ｅｎ[ ]
２ ＝０
Ｄｎ１＋ｎ[ ]
２ ＝Ｅ ｎ１＋ｎ２－( )０[ ]２ ＝Ｅｎ[ ]２
１ ＋２Ｅｎ１ｎ[ ]
２ ＋Ｅｎ[ ]２
２ ＝２
３．平稳随机过程
（１）严平稳和广义平稳随机过程
严平稳和广义平稳随机过程如表３－２所示。
１８　
表３－２　严平稳和广义平稳随机过程
名称 定义 性质
严平稳
随机过程 ξ( )ｔ的任意 ｎ维分布与时间
起点无关
一维分布与时间 ｔ无关；二维分布只与
时间间隔τ有关
广义平稳
ａ( )ｔ＝ａ
Ｒｔ１，ｔ１＋( )τ＝Ｒ( )τ
数学期望是个常数，与时间 ｔ无关；自相
关函数只与时间间隔τ有关
二者比较 严平稳或狭义平稳一定是广义平稳，反之不一定成立
　　（２）各态历经性
任取平稳随机过程ξ( )ｔ的任一样本函数ｘ( )ｔ，其时间均值和时间自相关满足
ａ－ ＝ｘ( )ｔ ＝ｌｉｍ
Ｔ→!
１
Ｔ∫
Ｔ／２
－Ｔ／２
ｘ( )ｔｄｔ＝ａ
Ｒ( )τ ＝ｘ( )ｔｘｔ＋( )τ ＝ｌｉｍ
Ｔ→!
１
Ｔ∫
Ｔ／２
－Ｔ／２
ｘ( )ｔｘｔ＋( )τｄｔ＝Ｒ( )τ
则称平稳随机过程ξ( )ｔ具有各态历经性。
意义：可用任意一次实现的“样本平均”来取代随机过程的“统计平均”，可用任意一次实现的功
率谱密度来取代随机过程的功率谱密度，简化测量和计算问题；具有各态历经性的随机过程一定是平
稳随机过程，反之不一定成立。
（２）平稳随机过程自相关函数的性质
平稳随机过程自相关函数的性质如表３－３所示。
表３－３　平稳随机过程自相关函数的性质
性质 含义
Ｒ( )０ ＝Ｅξ２( )[ ]ｔ ξ( )ｔ的平均功率
Ｒ( )τ＝Ｒ －( )τ 偶函数
Ｒ( )τ "
Ｒ( )０ Ｒ( )０ 是Ｒ( )τ的上界
Ｒ( )
!
＝Ｅξ( )ｔξｔ＋( )[ ]
!
＝Ｅ２ ξ( )[ ]ｔ ＝ａ２ ξ( )ｔ的直流功率
Ｒ( )０－Ｒ( )
!
＝σ２ ξ( )ｔ的交流功率
　　典型考研题（南京邮电大学２００８年）
平稳信号的方差，均值的平方和零时差的自相关分别代表　　　　　　　。
Ａ）直流功率，交流功率和平均功率
Ｂ）交流功率，直流功率和平均功率
Ｃ）平均功率，直流功率和交流功率
答案：Ｂ
樊昌信《通信原理》考研考点精讲
１９　
（４）维纳———辛钦定理
平稳随机过程ξ( )ｔ的自相关函数和功率谱密度Ｐξ( )ω 互为傅里叶变换对。
Ｐξ( )ω ＝∫
!
－
!
Ｒ( )τｅ－ｊωτｄτ＝Ｐξ( )ｆ
Ｒ( )τ＝
１
２π∫
!
－
!
Ｐξ( )ωｅｊωτｄω＝∫
!
－
!
Ｐξ( )ｆｅｊ２πｆτｄｆ
　　典型考研题（同济大学２００５年）
若随机过程ｚ( )ｔ＝ｍ( )ｔｃｏｓω０ｔ＋( )θ，其中ｍ( )ｔ是广义平稳随机过程，且自相关函数Ｒｍ( )τ为
Ｒｍ( )τ＝
１＋τ， －１＜τ＜０
１－τ， ０"τ＜１
０， 其它
{
τ
θ是服从均匀分布的随机变量，它与ｍ( )ｔ彼此统计独立。
１）证明ｚ( )ｔ是广义平稳的；
２）绘出自相关函数Ｒｚ( )τ的波形；
３）求功率谱密度Ｐｚ( )ω 及功率Ｓ。
４．高斯随机过程
（１）定义：任意ｎ维概率密度都服从正态分布的随机过程。
（２）重要性质：高斯过程若广义平稳，则必狭义平稳；高斯过程中的随机变量之间若不相关，则它
们统计独立；若干个高斯过程之和仍是高斯过程；高斯过程经线性变换后，仍是高斯过程。
（３）一维高斯概率密度函数及其分布函数
ｆ( )ｘ＝
１
２槡πσ
ｅｘｐ－
( )ｘ－ａ２
２σ( )２ ，称之为ｘ～Ｎａ，σ( )２
Ｆ( )ｘ＝Ｐξ( )＜ｘ＝∫
ｘ
－
!
ｆ( )ｘｄｘ
误差函数
ｅｒｆ（ｘ）＝ ２
槡π
∫
ｘ
０
ｅ－ｚ２ｄｚ
ｅｒｆｃ（ｘ）＝ ２
槡π
∫
!
ｘ
ｅ－ｚ２ｄｚ
ｅｒｆｃ（ｘ）＋ｅｒｆ（ｘ）＝１
Ｑ函数
Ｑ（ｘ）＝ １
２槡π
∫
!
ｘ
ｅ－ｚ２／２ｄｚ ｘ０
互补误差函数和Ｑ函数的关系
２０　
ｅｒｆｃ（ｘ）＝２Ｑ
槡２( )ｘ
５．平稳随机过程通过线性系统
平稳随机过程通过线性系统如图３－２所示。
（１）输出均值
ＥξＯ( )[ ]ｔ ＝Ｅξｉ( )[ ]ｔ·Ｈ( )０
（２）输出功率谱密度
ＰＯ( )ｆ＝Ｐｉ( )ｆ· Ｈ( )ω ２
（３）输出过程的自相关函数
Ｒｏ( )τ＝
１
２π∫
!
－
!
Ｐｏ( )ωｅｊωτｄω＝∫
!
－
!
Ｐｏ( )ｆｅｊ２πｆτｄｆ
典型考研题（同济大学２００４年）
已知高斯过程的均值为ａ，方差为σ２，功率谱密度为 ｎ０／２，其概率密度分布函数为　　　　　
　　，若通过Ｈ( )ω ＝ｋ０ｅ
－ｊωｔ的低通网络，则输出过程的均值为　　　，功率谱密度为　　　　。
答案：
ｆ( )ｘ＝
１
２槡πσ
ｅｘｐ－
( )ｘ－ａ２
２σ( )２ ；ＥξＯ( )[ ]ｔ ＝Ｅξｉ( )[ ]ｔ·Ｈ( )０ ＝ａｋ０；
ＰＯ( )ｆ＝Ｐｉ( )ｆ· Ｈ( )ω ２ ＝
ｎ０ｋ
２
０
２ Ｗ／Ｈｚ
６．窄带随机过程和正弦波加窄带随机过程
（１）窄带随机过程任一样本函数的功率谱密度和波形图如图３－３所示。
均值为０，方差为σ２的平稳高斯窄带随机过程的定义及性质如表３－４所示。
樊昌信《通信原理》考研考点精讲
２１　
表３－４　均值为０，方差为σ２的平稳高斯窄带随机过程的定义及性质
名称 定义 表达式或性质
窄
带
随
机
过
程
功率谱：Δｆｆｃ；ｆｃ０
任一样本函数波形：包络
和相位随机缓慢变化的近似正
弦波
ξ（ｔ）＝ａξ（ｔ）ｃｏｓωｃｔ＋φξ（ｔ[ ]）， ａξ( )ｔ０
ξ（ｔ）＝ξｃ（ｔ）ｃｏｓωｃｔ－ξｓ（ｔ）ｓｉｎωｃｔ
ξｃ（ｔ）＝ａξ（ｔ）ｃｏｓφξ（ｔ）同相分量
ξｓ（ｔ）＝ａξ（ｔ）ｓｉｎφξ（ｔ）　正交分量
ｆ（ａξ）＝
ａξ
σ２
ｅｘｐ－
ａ２ξ
２σ２[ ]
ξ
， ａξ０瑞利衰落
ｆ（φξ）＝
１
２π
， φξ∈（－π，π）均匀分布
ｆ（ａξ，φξ）＝ｆ（ａξ）ｆ（φξ）统计独立
Ｒｓｃ（０）＝Ｒｃｓ（０）　ξｃ（ｔ）和ξｓ（ｔ）在同一时刻
对应的随机变量不相关，由于是高斯的，因此，统计
独立。
ξｃ（ｔ）
带宽为 Δｆ／２的低通平稳高斯
随机过程
Ｅξｃ( )[ ]ｔ ＝０；σ２ｃ ＝σ
２
ξｓ（ｔ）
带宽为 Δｆ／２的低通平稳高斯
随机过程
Ｅξｓ( )[ ]ｔ ＝０；σ２ｓ ＝σ
２
　　（２）正弦波加窄带随机过程
ｒ（ｔ）＝Ａｃｏｓ（ωｃｔ＋θ）＋ｎ（ｔ）
＝Ａｃｏｓ（ωｃｔ＋θ）＋ｎｃ（ｔ）ｃｏｓωｃｔ－ｎｓ（ｔ）ｓｉｎωｃｔ
＝［Ａｃｏｓθ＋ｎｃ（ｔ）］ｃｏｓωｃｔ－［Ａｓｉｎθ＋ｎｓ（ｔ）］ｓｉｎωｃｔ
＝ｚ( )ｔｃｏｓωｃｔ＋φ( )( )ｔ ， ｚ( )ｔ０
包络ｚ( )ｔ服从广义瑞利分布。
典型考研题（海军潜艇学院２００９年）
均值为０的窄带平稳高斯噪声加上一个正弦信号，它们相加之后的包络一维分布服从　Ｄ　 。
Ａ．高斯分布　　　　Ｂ．均匀分布　　　　Ｃ．瑞利分布　　　　Ｄ．莱斯分布
７．高斯白噪声和带限白噪声
高斯白噪声和带限白噪声的定义，功率谱密度和自相关函数如表３－５所示。
２２　
表３－５　高斯白噪声和带限白噪声
名称 定义 功率谱密度和功率 自相关函数
白
噪
声
噪声的功
率谱密度
在所有频
率上均为
一常数
Ｐｎ( )ｆ＝
ｎ０
２， －
!
＜ｆ＜
!
Ｐｎ( )ｆ＝ｎ０， ０＜ｆ＜!
白噪声只有在同一时刻才相关，在其
他任意两个时刻上随机变量都是不
相关的。
高斯白
噪声
白噪声在任一时刻的随机变量的取值服从高斯分布，其它同白噪声。
低
通
白
噪
声
白噪声经
过理想低
通滤波器
或理想低
通信道后
的输出
Ｐｎ（ｆ）＝
ｎ０
２，ｆ"ｆＨ
０，
{
其它
Ｎ＝
ｎ０
２×２ｆＨ ＝ｎ０ｆＨ
Ｒ（τ）＝ｎ０ｆＨＳａ２πτ·
ｆＨ( )２
按抽样定理ｆｓ＝２ｆＨ对低通白噪声抽
样的话，各抽样值是互不相关的随机
变量。
带
通
白
噪
声
白噪声经
过理想带
通滤波器
或理想带
通信道后
的输出
Ｐｎ（ｆ）＝
ｎ０
２，ｆｃ－
Ｂ
２" ｆ"ｆｃ＋
Ｂ
２
０，
{
其它
Ｎ＝
ｎ０
２×２Ｂ＝ｎ０Ｂ
Ｒ( )τ＝ｎ０Ｂｓａ２πτ×
Ｂ( )２ ｃｏｓωｃτ
樊昌信《通信原理》考研考点精讲
２３　
典型考研题１（西安邮电大学２００９年）
窄带高斯白噪声中的“窄带”、“高斯”、“白”的含义各是什么？
答案：“窄带”是指噪声带宽Δｆｆｃ，中心频率ｆｃ０；“高斯”是指该噪声的概率密度函数服从高
斯分布；“白”是指噪声的功率谱密度在所有频率上均为一常数。
典型考研题２（西安邮电大学２０１０年）
一个中心频率为ｆｃ，带宽为Ｂ的理想带通滤波器如图１所示。假设输入是均值为０，双边功率谱
密度为ｎ０／２的高斯白噪声，试求：
１）求滤波器输出噪声的自相关函数；
２）滤波器的输出噪声的平均功率；
３）求输出噪声的一维概率密度函数。
２４　
? 第四章
信　道
１．信道的主要分类及定义
信道的主要分类及定义如表４－１所示。
表４－１　信道的主要分类及定义
名　称 定　义 分类及性质
狭义信道 各种物理传输媒介 分为有线信道和无线信道
广义信道
信道范围扩大后（传输媒介、发送
和接收设备）的信道
分为调制信道和编码信道
调制信道
发送端调制器输出端到接收端解
调器输入端
分为恒参信道和随参信道
ｅ０（ｔ）＝ｋ（ｔ）·ｅｉ（ｔ）＋ｎ（ｔ）
ｋ( )ｔ乘加性干扰
ｎ( )ｔ加性干扰
樊昌信《通信原理》考研考点精讲
２５　
编码信道
发送端编码器输出端到接收端译
码器输入端
Ｐ（０／０）＋Ｐ（１／０）＝１
Ｐ（１／１）＋Ｐ（０／１）＝１
恒
参
信
道

对
所
传
信
信
号
的
影
响
及
改
进
措
施

无
失
真
传
输
条
件
ｋ( )ｔ ～ｔ不变或慢变
等效为线性时不变网络
Ｈ（ω）＝ Ｈ（ω）ｅｊφ（ω）
幅频失真
模拟信号：波形失真→信噪比下降
数字信号：码间串扰→
{ }
引起误码
采用幅度均衡器减小失真
相频失真
模拟信号：不影响话音信号，影响
视频信号
数字信号：码间串扰→










引起误码
采用相位均衡器减小失真
无失真传输条件
Ｈ（ω） ＝Ｋ　　φ( )ω ＝－ωｔｄ　τ（ω）＝
ｄφ（ω）
ｄω
＝－ｔｄ
典型恒参
信道例子
有线信道（明线、对称电缆、同轴电缆、光纤）、中长波地波传播、卫星中继、光波视
距中继
２６　
典型考研题１（江西理工大学２０１０年）
广义信道可以分为　　　　　信道和　　　　　　信道。
答案：调制；编码
典型考研题２（南京邮电大学２０１０年）
樊昌信《通信原理》考研考点精讲
２７　
恒参信道的不理想会引起信号的　　　，从而产生　　　。
Ａ．高频失真，信号畸变　　　　　　Ｂ．脉冲展宽，码间干扰
Ｃ．低频失真，相位失真　　　　　　Ｄ．码间干扰，频率失真
答案：Ｂ
典型考研题３（沈阳工业大学２０１１）
设一恒参信道的幅频特性和相频特性分别为
Ｈ( )ω ＝Ｋ０
φ( )ω ＝－ωｔ
{
ｄ
其中，Ｋ０和ｔｄ都是常数，试确定信号ｓ( )ｔ通过该信道后输出信号的时域表示式，并讨论之。
解：
Ｈ( )ω ＝ Ｈ( )ω ｅｊφ( )ω ＝Ｋ０ｅ
－ｊωｔｄ
ｈ( )ｔ＝Ｋ０δｔ－ｔ( )
ｄ
ｓｏ( )ｔ＝ｓ( )ｔｈ( )ｔ＝ｓ( )ｔＫ０δｔ－ｔ( )
ｄ ＝Ｋ０ｓｔ－ｔ( )
ｄ
由于该恒参信道满足无失真传输条件，因此，信号ｓ( )ｔ通过该信道后输出的信号不会发生失真。
典型考研题４（西安电子科技大学２０１１）
随参信道传输媒介的特点是什么？随参信道对信号传输有什么影响？
答案：随参信道传输媒介的特点是信号的衰耗随时间随机变化；信号传输的时延随时间随机变
化；多径传播。随参信道对信号传输的影响是瑞利衰落；频率弥散；频率选择性衰落
２．信道容量
离散信道容量和连续信道容量如表４－２所示。
（图表见视频）
典型考研题１（江西理工大学２０１１）
连续信道的信道容量受　　　　 、　　　　　 、和　　　　 等“三要素”的限制。
答案：信道带宽Ｂ；接收信号功率Ｓ；信道噪声单边带功率谱密度ｎ０
典型考研题２（西安邮电大学２００９）
设信源由两种符号“０”和“１”组成，符号传输速率为１０００波特，且这两种符号的出现概率相等，均
为０．５。信道为对称信道，其传输的符号错误概率为 １／６４。试画出此信道模型，并求此信道的容
量Ｃｔ。
解：信道模型
２８　
可知
ｐｘ１／ｙ( )
１ ＝６３／６４，ｐｘ２／ｙ( )
１ ＝１／６４
ｐｘ２／ｙ( )
２ ＝６３／６４，ｐｘ１／ｙ( )
２ ＝１／６４
Ｈ（ｘ）＝－∑
２
ｉ＝１
Ｐ（ｘｉ）ｌｏｇ２Ｐ（ｘｉ）
＝－ １
２ｌｏｇ２
１
２＋
１
２ｌｏｇ２[ ]１２ ＝１（比特／符号）
Ｈ（ｘ／ｙ）＝－∑
２
ｊ＝１
Ｐ（ｙｊ）∑
２
ｉ＝１
Ｐ（ｘｉ／ｙｊ）ｌｏｇ２Ｐ（ｘｉ／ｙｊ）］
＝－｛Ｐ（ｙ１）Ｐ（ｘ１／ｙ１）ｌｏｇ２Ｐ（ｘ１／ｙ１）＋Ｐ（ｘ２／ｙ１）ｌｏｇ２Ｐ（ｘ２／ｙ１[ ]）
＋Ｐ（ｙ２）Ｐ（ｘ１／ｙ２）ｌｏｇ２Ｐ（ｘ１／ｙ２）＋Ｐ（ｘ２／ｙ２）ｌｏｇ２Ｐ（ｘ２／ｙ２[ ]）｝
＝－ （６３／６４）ｌｏｇ２（６３／６４）＋（１／６４）ｌｏｇ２（１／６４[ ]）
＝０．１２（比特／符号）
平均信息量／符号 ＝Ｈ（ｘ）－Ｈ（ｘ／ｙ）
＝０．８８（比特／符号）
Ｃ＝ｍａｘ
Ｐ（ｘ）
［Ｈ（ｘ）－Ｈ（ｘ／ｙ）］＝０．８８（比特／符号）
Ｃｔ＝Ｃ·ＲＢ ＝０．８８×１０００＝８８０（比特／秒）
典型考研题３（西安邮电大学２０１０）
已知黑白电视图像信号每帧有３×１０５个像素组成，设每个像素有２５６个亮度等级；如果所有的亮
度等级出现的机会相等，并统计独立；
１）试计算每秒传输２０幅画面所需的信道容量；
２）如果接收信噪比为３０ｄＢ，为了传输该图像所需的最小带宽。
解：１）因为每个像素独立地以等概率取２５６个亮度电平，故每个像素的信息量为
ＩＰ ＝－ｌｏｇ２
１
２５６＝８（比特／像素）
每幅图像的信息量为
ＩＦ ＝３×１０
５×８＝２．４×１０６（比特／幅）
因为每秒传输２０幅图像，所以要求传输速率为
Ｒｂ ＝２０×ＩＦ ＝２０×２．４×１０
６ ＝４．８×１０７（比特／秒）
信道的容量Ｃｔ必须不小于该传信率。
ＣｔＲｂ ＝４．８×１０
７（比特／秒）
２）
Ｓ( )Ｎ ｄＢ
＝１０ｌｇＳＮ ＝３０，
Ｓ
Ｎ ＝１０００
樊昌信《通信原理》考研考点精讲
２９　
Ｒｂ"Ｃｔ＝Ｂｌｏｇ２ １( )＋Ｓ／Ｎ
Ｂ
Ｒｂ
ｌｏｇ２ １( )＋Ｓ／Ｎ
＝ ４．８×１０７
ｌｏｇ２ １＋( )１０００
＝４．８×１０
７
９．９７ ≈４．８ＭＨｚ
Ｂｍｉｎ ＝４．８ＭＨｚ
故所需最小信道带宽为４．８ＭＨｚ
３０　
? 第五章
模拟通信系统
１．调制的定义、目的和分类
调制的定义、目的如表５－１所示。
表５－１　调制的定义、目的
名称 定义 目的
调制
用调制信号去控制载波参数，
把信号转换成适合在信道中
传输的形式的过程。
①把调制信号转换成适合在信道中传输的已调信号。
②实现信道的多路复用，提高信道利用率。
③改善系统抗噪声性能。
线性调制
已调信号频谱只是调制信号频谱的简单搬移，频谱形状保持不变。（ＡＭ、ＤＳＢ－ＳＣ、
ＳＳＢ、ＶＳＢ、ＭＡＳＫ、ＭＰＳＫ、ＭＦＳＫ、ＱＡＭ、ＭＳＫ、ＧＭＳＫ等）
模
拟
信
号
线
性
调
制
模
型
①滤波法　
ｓｍ（ｔ）＝［ｍ（ｔ）ｃｏｓωｃｔ］ｈ（ｔ）
适当选择ｈ( )ｔ，便可得到各种幅度调制信号，例如，当Ｈ( )ω ＝１，即为全通网络时，
可以得到ＡＭ和ＤＳＢ信号。
②移相法
ｓｍ（ｔ） ＝ ｓＩ（ｔ）ｃｏｓωｃｔ＋ ｓＱ（ｔ）ｓｉｎωｃｔ　 　ｓＩ（ｔ） ＝ ｈＩ（ｔ）ｍ（ｔ）；ｓＱ（ｔ） ＝
ｈＱ（ｔ）ｍ（ｔ）　　ｈＩ（ｔ）＝ｈ（ｔ）ｃｏｓωｃｔ；ｈＱ（ｔ）＝ｈ（ｔ）ｓｉｎωｃｔ
非线
性调制
已调信号频谱不再是只是调制信号频谱的简单搬移，而是频谱的非线性变换。
（ＦＭ、ＰＭ）
樊昌信《通信原理》考研考点精讲
３１　
　　典型考研题（北京科技大学２０１１年）
在模拟通信系统中，为什么要进行正弦载波调制？
答案：把调制信号转换成适合在信道中传输的已调信号；实现信道的多路复用，提高信道利用率；
改善系统抗噪声性能。
２．ＡＭ系统
ＡＭ系统的调制解调原理及抗噪声性能如表５－２所示。
表５－２　ＡＭ系统的调制解调原理及抗噪声性能
３２　
樊昌信《通信原理》考研考点精讲
３３　
３４　
樊昌信《通信原理》考研考点精讲
３５　
　　典型考研题１（海军潜艇学院２００９年）
已知某调幅信号的展开式为
ｓＡＭ( )ｔ＝０．１２５ｃｏｓ２π１０( )４ ｔ＋４ｃｏｓ２π１．１×１０( )４ ｔ＋０．１２５ｃｏｓ２π１．２×１０( )４ ｔ
则载波信号的表达式为　　　　　　　　　　　；调制信号表达式为　　　　　。
答案：
ｓＡＭ( )ｔ＝ Ａ＋ｍ( )[ ]ｔ ｃｏｓ２πｆｃｔ
＝０．１２５ｃｏｓ２π１０( )４ ｔ＋４ｃｏｓ２π１．１×１０( )４ ｔ＋０．１２５ｃｏｓ２π１．２×１０( )４ ｔ
＝ ４＋０．２５ｃｏｓ２π１０( )３[ ]ｔｃｏｓ２π１．１×１０( )４ ｔ
载波信号的表达式ｃｏｓ２π１．１×１０( )４ ｔ；
调制信号表达式０．２５ｃｏｓ２π１０( )３ ｔ。
典型考研题２（江西理工大学２０１１）
什么是门限效应？ＡＭ信号采用包络检波法解调时为什么会产生门限效应？
答案：输出信噪比不是按比例随着输入信噪比的下降，而是发生了急剧恶化，称之为门限效应。
是由包络检波器的非线性解调作用引起的。
典型考研题３（西安电子科技大学２０１０年）
采用包络检波的ＡＭ系统中，若噪声的双边带功率谱密度为 ５×１０－( )５ ｍＷ／Ｈｚ，单频正弦波调制
时载频功率为１００ｍＷ，边带功率为每边带２０ｍＷ，包络检波器前的带通滤波器带宽为４ＫＨｚ
１）画出ＡＭ系统调制与解调框图；
２）求解调器输出信噪比和调制制度增益；
３）若受到信道衰减影响，当输入信噪比持续下降时，解调器会出现什么现象，为什么？
解：１）ＡＭ系统调制与解调框图
２）包络检波器输入信号功率
Ｓｉ＝Ｐｃ＋Ｐｓ＝１００＋２×２０＝１４０ｍＷ
包络检波器输入噪声功率
Ｎｉ＝
ｎ０
２×２ＢＢＰＦ ＝５×１０
－５×２×４×１０３ ＝０．４ｍＷ
Ｓｉ
Ｎｉ
＝１４００．４＝３５０
包络检波器输出信号功率
Ｓｏ ＝２Ｐｓ＝８０ｍＷ
３６　
包络检波器输出噪声功率
Ｎｏ ＝Ｎｉ＝０．４ｍＷ
包络检波器输出信噪比
Ｓｏ
Ｎｏ
＝８０００．４＝２００
调制增益
ＧＡＭ ＝
Ｓｏ／Ｎｏ
Ｓｉ／Ｎｉ
＝２００３５０＝
４
７
３）产生门限效应，是由于包络检波器的非线性解调作用引起来的。
３．ＤＳＢ－ＳＣ系统
ＤＳＢ－ＳＣ系统的调制解调原理及抗噪声性能如表５－３２所示。
（图表见视频）
典型考研题（江西理工大学２０１１年）
设某信道具有均匀的双边带功率谱密度Ｐｎ( )ｆ＝０．５×１０－３Ｗ／Ｈｚ，在该信道中传输抑制载波的双
边带信号，并设调制信号带宽限制在５ＫＨｚ，而载波频率１００ＫＨｚ，已调信号达到接收端时的功率是
１０ＫＷ。若接收机的输入信号在加至解调器之前，先经过一个理想带通滤波器。试问：
１）该理想带通滤波器应具有怎样的传输特性Ｈ( )ω ；
２）解调器输入端的信噪功率比；
３）解调器输出端的信噪功率比；
４）求出接收端输出噪声的双边带功率谱密度，并用图形表示出来。
４．ＳＳＢ系统
ＳＳＢ系统的调制解调原理及抗噪声性能如表５－３所示。
（图表见视频）
典型考研题（西安电子科技大学２００９年）
在模拟通信系统中，单边带信号通过恒参信道到达接收端的输入信号为
ｓＳＳＢ( )ｔ＝ｋｍ( )ｔｃｏｓωｃｔ－ｍ( )ｔ
∧
ｓｉｎωｃ[ ]ｔ
基带信号的功率谱密度为
Ｐｍ( )ｆ＝
αｆ
ｆｍ
， ｆ"ｆｍ
０， ｆ＞ｆ
{
ｍ
其中，α和ｆｍ都是常数，信道加性高斯白噪声的双边带功率谱密度为ｎ０／２。
１）画出相移法调制器的原理框图；
樊昌信《通信原理》考研考点精讲
３７　
２）试画出对单边带信号进行解调的相干解调原理框图；
３）求相干解调器的输出信噪比。
５．ＤＳＢ和 ＳＳＢ系统抗噪声性能比较
ＤＳＢ和ＳＳＢ系统抗噪声性能比较如表５－４所示。
表５－４　ＤＳＢ和ＳＳＢ系统抗噪声性能比较
条件
调制信号带宽相同为ｆｍ，解调器输入信号平均功率相同，均为Ｓｉ，信道噪声带边带功
率谱密度相同，均为ｎ０。
名称 输出信噪比 结论
ＤＳＢ
Ｓｏ
Ｎｏ
＝
Ｓｉ／２
Ｎｉ／４
＝
Ｓｉ／２
２ｎ０ｆｍ／４
＝
Ｓｉ
ｎ０ｆｍ
ＳＳＢ
Ｓｏ
Ｎｏ
＝
Ｓｉ／４
Ｎｉ／４
＝
Ｓｉ／４
ｎ０ｆｍ／４
＝
Ｓｉ
ｎ０ｆｍ
输出信噪比决定抗噪声性能，
虽然双边带的调制增益是单
边带的２倍，但在相同的条件
下，二者的输出信噪比相同，
说明抗噪声性能相同。
　　典型考研题（海军潜艇学院２００９年）
ＤＳＢ和ＳＳＢ调制系统的抗噪声性能是否相同？为什么？
答案：相同
在调制信号带宽相同为ｆｍ，解调器输入信号平均功率相同，均为Ｓｉ，信道噪声带边带功率谱密度
相同，均为ｎ０时，对于
ＤＳＢ
Ｓｏ
Ｎｏ
＝
Ｓｉ／２
Ｎｉ／４
＝
Ｓｉ／２
２ｎ０ｆｍ／４
＝
Ｓｉ
ｎ０ｆｍ
ＳＳＢ
Ｓｏ
Ｎｏ
＝
Ｓｉ／４
Ｎｉ／４
＝
Ｓｉ／４
ｎ０ｆｍ／４
＝
Ｓｉ
ｎ０ｆｍ
在相同的条件下，二者的输出信噪比相同，说明抗噪声性能相同。
６．ＶＳＢ系统
ＶＳＢ系统如表５－５所示。
（图表见视频）
典型考研题（西安电子科技大学２００１年）
在残留边带系统中，为了无失真恢复调制信号，其传输函数Ｈ( )ω 应满足　　　　　　　　。
答案：Ｈ（ω＋ωｃ）＋Ｈ（ω－ωｃ）＝常数， ω "ωＨ
３８　
７．ＦＭ系统
（１）ＦＭ和ＰＭ的基本概念
ＦＭ和ＰＭ的基本概念如表５－６所示。
表５－６　ＦＭ和ＰＭ的基本概念
名称 表达式 含义
角度调制 ｓｍ（ｔ）＝Ａｃｏｓ［ωｃｔ＋φ（ｔ）］
瞬时相位 ωｃｔ＋φ（ｔ）
瞬时相偏 φ（ｔ）
瞬时角频率 ｄ［ωｃｔ＋φ（ｔ）］／ｄｔ＝ωｃ＋ｄφ（ｔ）／ｄｔ
瞬时频率 ｆｃ＋ｄφ（ｔ）／２πｄｔ
瞬时角频偏 ｄφ（ｔ）／ｄｔ
瞬时频偏
ｄφ（ｔ）
２πｄｔ
ＦＭ
ｄφ（ｔ）／ｄｔ＝Ｋｆｍ( )ｔ
Ｋｆ—调频灵敏度，单位调制信
号幅度引起 ＦＭ信号的角频率偏移
量，单位ｒａｄ／（ｓ
#
Ｖ）。
ｓＦＭ（ｔ） ＝ Ａｃｏｓ［ωｃｔ ＋ Ｋｆ
∫
ｔ
－
!
ｍ（τ）ｄτ］
是指瞬时角频率偏移随基带信号而
线性变化。
ＰＭ
φ（ｔ）＝Ｋｐｍ( )ｔ
Ｋｐ—调相频灵敏度，单位调制
信号幅度引起 ＰＭ信号的相位偏移
量，单位ｒａｄ／Ｖ。
ｓＰＭ（ｔ）＝Ａｃｏｓ［ωｃｔ＋Ｋｐｍ( )ｔ］
是指瞬时相位偏移随基带信号而线
性变化。
　　（２）单频调制信号条件下ＦＭ和ＰＭ的比较
单频调制信号条件下ＦＭ和ＰＭ的比较如表５－７所示。
（图表见视频）
典型考研题１（天津工业大学２００７年）
已知调频信号ｓＦＭ( )ｔ＝１０ｃｏｓ１０６πｔ＋８ｃｏｓ１０３π[ ]ｔ调制器的调频常数 Ｋｆ＝２，其载频为　　　
　，调频指数为　　　，最大频偏为　　　 ，调制信号ｆ( )ｔ为　　　　　　　　　 。
樊昌信《通信原理》考研考点精讲
３９　
典型考研题２（西安邮电大学２０１２年）
已知某调频波的振幅是２Ｖ，瞬时频率为：
ｆ（ｔ）＝１０６＋２×１０４ｃｏｓ４π×１０３ｔＨｚ
试确定：
１）此调频波的时域表达式；
２）此调频波的最大频偏、调频指数和频带宽度。
典型考研题１（南京邮电大学２０１０年）
下列模拟通信系统中目前在广播中还在广泛应用的是　 Ｃ　　 。
Ａ）相干ＡＭ　　　　　Ｂ）ＤＳＢ　　　　　 Ｃ）ＦＭ　　　　　Ｄ）ＶＳＢ
答案：Ｃ
典型考研题２（西安电子科技大学２００１年）
当调频指数满足　　　　　　　　　 称为窄带调频。
答案： Ｋｆ∫
ｔ
－
!
ｍ（τ）ｄτ＜＜
π
６
典型考研题３（西安邮电大学２０１０）
在下图３所示的宽带调频方案中，设调制信号是 ｆｍ ＝５ｋＨｚ的单频余弦信号，ＮＢＦＭ信号的载频
ｆ１ ＝１００ｋＨｚ，最大频偏 Δｆ１ ＝１０Ｈｚ；混频器参考频率 ｆ２ ＝５ＭＨｚ，选择倍频次数 ｎ１ ＝６４，ｎ２ ＝４８，
试求：
１）求ＮＢＦＭ信号的调频指数；
２）求宽带ＷＢＦＭ信号最大频偏和调频指数。
解：１）ＮＢＦＭ信号的调频指数为
ｍｆ＝
Δｆ１
ｆｍ
＝ １０
５×１０３
＝２×１０－３
２）ＷＢＦＭ信号的最大频偏为
Δｆ＝ｎ１ｎ２Δｆ１ ＝６４×４８×１０＝３０．７２ＫＨｚ
调频指数为
ｍｆ＝
Δｆ
ｆｍ
＝３０．７２×１０
３
５×１０３
＝６．１４４
８．预加重与去加重
预加重与去加重如表５－８所示。
４０　
表５－８　预加重与去加重
原
因
及
措
施
由宽带调频系统鉴频器输出噪声谱密度呈抛物线形状可知，解调器输出噪声随调制信号
频率升高而增强，而调制信号的幅度随频率升高而减小，因此，解调器恢复的信号在高频
部分信噪比变差。为提高恢复信号在高频部分的信噪比，常采用“预加重”和“去加重”
技术，在保持恢复信号高频部分功率不变的条件下，减小噪声的平均功率，从而改善高频
部分的输出信噪比。
系
统
框
图
Ｈｐ( )ｆ＝
１
Ｈｄ( )ｆ
举
例
录音和放音设备中的杜比（Ｄｏｌｂｙ）降噪系统
　　典型考研题（河北大学２０１０年）
调频信号经过解调后的输出噪声与调幅信号经过解调后的输出噪声特性与频率有关么？若有，
可采用什么技术对它进行改善？
答案：调频信号经过解调后的输出噪声与频谱特性有关，调幅信号经过解调后的输出噪声特性与
频率无关。对于调频信号，可以采用去加重和预加重技术进行解决。
９．具有衰耗的模拟通信系统
具有衰耗的模拟通信系统如表５－９所示。
表５－９　具有衰耗的模拟通信系统
Ｓｏ
Ｎｏ
调制增益
}
Ｇ

Ｓｉ
Ｎｉ
Ｎｉ＝ｎｏ
}
Ｂ

Ｓｉ}
α

ＳＴ}
α

Ｓｉ
Ｎｉ＝ｎｏ
}Ｂ
Ｓｉ
Ｎｉ
调制增益
}
Ｇ

Ｓｏ
Ｎｏ
樊昌信《通信原理》考研考点精讲
４１　
　　典型考研题１（天津工业大学２００７年）
已知调制信号的带宽为１５ＫＨｚ，采用ＡＭ调制，调制制度增益ＧＡＭ ＝２／３，载波频率为３０ＭＨｚ，信
道为高斯白噪声，其双边带功率谱密度为ｎ０／２＝１０
－１２Ｗ／Ｈｚ，信道使信号衰减５０ｄＢ，求在保证接收机
输出信噪比为５０ｄＢ时，发射机最低发射功率应为多少？
解：
Ｓ０
Ｎ( )
０ ｄＢ
＝１０ｌｇ
Ｓ０
Ｎ０
＝５０　　
Ｓ０
Ｎ０
＝１０５
α＝ ＳＴ
Ｓ( )
ｉ ｄＢ
＝１０ｌｇ
ＳＴ
Ｓｉ
＝５０　　
ＳＴ
Ｓｉ
＝１０５
ＢＡＭ ＝２ｆｍ ＝３０ＫＨｚ
ＧＡＭ ＝
Ｓ０／Ｎ０
Ｓｉ／Ｎｉ
＝２／３　
Ｓｉ
Ｎｉ
＝３２×
Ｓ０
Ｎ０
＝１．５×１０５
Ｎｉ＝
ｎ０
２×２ＢＡＭ ＝１０
－１２×２×３０×１０３ ＝６×１０－８（Ｗ）
Ｓｉ＝１．５×１０
５Ｎｉ＝１．５×１０
５×６×１０－８ ＝９×１０－３（Ｗ）
ＳＴ ＝１０
５Ｓｉ＝９００（Ｗ）
１０．模拟调制系统性能比较
模拟调制系统性能比较如表５－１０所示。
表５－１０　模拟调制系统性能比较
抗噪声性能 ＦＭ最好；ＤＳＢ和ＳＳＢ、ＶＳＢ一样；ＡＭ最差
频率利用率 ＳＳＢ最高；ＶＳＢ次较高；ＡＭ和ＤＳＢ一样；ＦＭ最差
功率利用率 ＦＭ最高；ＤＳＢ和ＳＳＢ、ＶＳＢ一样；ＡＭ最差
设备复杂度 ＳＳＢ最复杂；ＶＳＢ较复杂；ＤＳＢ／ＦＭ次之；ＡＭ最简单
　　１１．ＦＤＭ和立体声广播
（１）ＦＤＭ及其带宽的计算如表５－１１所示。
４２　
表５－１１　ＦＤＭ及其带宽的计算
定
义
按频率来划分信道的复用方式
框
图
频
谱
及
带
宽
Ｂｎ ＝ｎｆｍ ＋（ｎ－１）ｆｇ
优
缺
点
优点：是信道复用率高，容许复用的路数多，分路也很方便。因此，它成为目前模拟通信
中最主要的一种复用方式。
缺点：设备生产比较复杂，会因滤波器件特性不够理想和信道内存在非线性而产生路间
干扰。
　　（２）立体声广播
立体声广播如表５－１２所示。
樊昌信《通信原理》考研考点精讲
４３　
表５－１２　立体声广播
频
谱
结
构
原
理
框
图
樊昌信《通信原理》考研考点精讲
１０５　
（ＦＥＣ）、反馈重传（ＡＲＱ）和混合纠错（ＨＥＣ）。
答案：可靠性
２．载波同步
（１）外同步（插入导频法）
①适用范围
不包含载频分量的的信号，如抑制载波的ＤＳＢ、ＶＳＢ、等概的２ＰＳＫ和２ＤＰＳＫ等。
特例：单边带信号（ＳＳＢ）既没有载频分量又不能用直接法提取载波，只能用插入导频法。
②示意图
注意：插入导频为“正交载波”与发送端用于调制的本地载波移相９０°。
③原理框图
（２）自同步法（直接法）
①平方变换和平方环法
ｉ原理
设接收信号为
ｍ( )ｔｃｏｓωｃｔ
其中，Ｅｍ( )[ ]ｔ ＝０。
ｍ( )ｔｃｏｓωｃ[ ]ｔ２ ＝１２ｍ
２( )ｔ＋
１
２ｍ
２( )ｔｃｏｓ２ωｃｔ
２倍频
二倍频中，Ｅｍ２( )[ ]ｔ ≠０，可以将二倍频提取出来。
ｉ平方环法
由于窄带滤波器难以实现，常用锁相环代替。
１０６　
ｉｉ缺点
相位模糊：是由分频器的随机初始状态不确定导致的，其输出电压有相差１８０度的两种可能。可
采用２ＤＰＳＫ克服。
错误锁定：使锁相环锁定在其它离散的频率上。可通过降低环路波器的带宽来解决。
典型考研题１（西安电子科技大学２０１１年）
画出平方环原理框图，并指出采用此方案提取２ＰＳＫ信号载波时，存在什么缺点？在２ＤＰＳＫ解调
中如何克服此缺点？
答案：平方环原理框图
该方法在提取２ＰＳＫ信号的载波时存在相位模糊，采用相对调相可以解决该问题。
②科斯塔斯环（Ｃｏｓｔａｓ）
ｉ原理框图
ｉ表达式
设ｓ( )ｔ＝ｍ( )ｔｃｏｓωｃｔ＋( )θ
ｖａ ＝ｃｏｓ（ωｃｔ＋φ）；ｖｂ ＝ｃｏｓ（ωｃｔ＋φ＋
π
２）＝－ｓｉｎ（ωｃｔ＋φ）
ｖｅ＝
１
２ｍ（ｔ）ｃｏｓ（θ－φ）；ｖｆ＝
１
２ｍ（ｔ）ｓｉｎ（θ－φ）
ｖｇ ＝
１
８ｍ
２（ｔ）ｓｉｎ２（θ－φ）
樊昌信《通信原理》考研考点精讲
１０７　
当ｍ( )ｔ＝±１时，
ｖｇ≈
１
４（θ－φ）
环路滤波器为窄带低通滤波器，其截止频率很低，只允许ｖｇ中近似直流的电压分量通过。
③科斯塔斯环和平方环的比较
ｉ科斯塔斯环工作在载波频率上，而平方环的工作频率是载频的２倍，当载频较高时，科斯塔斯环
容易实现。
ｉ科斯塔斯环本身同时兼有提取载波和相干解调的作用，而平方环没有。
ｉｉ两者具有相同的鉴相特性
ｖｄ ＝ｋｄｓｉｎ２θ－( )φ
都具有相位模糊问题。Ｍ次方环或Ｍ相科斯塔斯环，具有２π／Ｍ的相位模糊。
ｉｖ这两种方法广泛应用于抑制载波的双边带信号（ＤＳＢ－ＳＣ，等概的２ＰＳＫ和２ＤＰＳＫ等）建立载
波同步。
④载波同步的性能指标
载波同步的性能指标有三种，如表１３－２所示。
表１３－２　载波同步的性能指标
相
位
误
差
稳态相差：
由电路参量引起
①窄带滤波器有单谐振电路构成
Δφ＝２ＱΔｆｆｑ
，Δｆ＝ｆｑ－ｆｃ，ｆｑ为谐振回路中心频率。
为减小稳态相差，应降低谐振电路的品质因数Ｑ。
②锁相环提取载波
Δφ＝Δｆｋｄ
，Δｆ＝ｆｃ－ｆ０，ｆ０为ＶＣＯ输出频率。
为减小稳态相差，应增加锁相环路直流增益ｋｄ。
随机相差：
由噪声引起
随机噪声方差：θ２ｒ ＝
１
２ｒ，ｒ信噪比
总
相
差
φ＝Δφ＋ θ２槡ｒ ＝Δφ＋σφ，σφ为相位抖动。
对于单谐振回路而言，Ｑ越低，Δφ越小，但θｒ越大。
１０８　
同步
建立时间
从开始接收到信号或失步状态到提取稳定的载频所需的时间。该时间越短
越好。
同步
保持时间
同步建立后，从失去接收信号时到失去载频同步的时间。该时间越长越好。
同步顺序 先建立载波同步，然后是码元同步，接着是群同步
　　典型考研题（西安电子科技大学２０１２年）
在接收端，提取位同步、帧同步和载波同步的先后顺序是　　　　。
答案：载波同步、码元同步、群同步
⑤载波相位误差对解调性能的影响—信噪比下降
ｉ对双边带信号的影响（ＡＭ、ＤＳＢ、２ＰＳＫ）
对于ＡＭ和ＤＳＢ，当载波相位误差为φ时，解调器输出信号为
ｍ′( )ｔ＝
１
２ｍ
( )ｔｃｏｓφ
不影响输出噪声功率，输出信号幅度衰减ｃｏｓφ倍，输出信噪比下降ｃｏｓ２φ倍。
对于２ＰＳＫ，当载波相位误差为φ时，解调器输出信号能量为
Ｅ′＝Ｅｃｏｓ２φ
误码率增加为
Ｐｅ＝
１
２ｅｒｆｃ
Ｅ
ｎ槡０
ｃｏｓ( )φ
ｉ对单边带及残留边带信号的影响—波形失真
对于ＳＳＢ，当载波相位误差为φ时，解调器输出信号为
ｍ′( )ｔ＝
１
４ｍ
( )ｔｃｏｓφ±
１
４ｍ
( )ｔ
∧
ｓｉｎφ
其中，第一项受到了ｃｏｓφ的衰减，第二项是正交项，使接收信号产生失真，失真程度随相位误差
的增加而增大，但输出有用信号和噪声的平均功率下降。
３．码元（或位）同步
（１）外同步
频域插入法：在发送的基带信号中插入频率为码元速率或码元速率倍数的同步信号。
樊昌信《通信原理》考研考点精讲
１０９　
（２）自同同步法
①开环同步法
将解调后的基带信号先进性某种线性变换，使其频谱中含有离散的定时信息，再通过窄带滤波器
滤除。又称之为非线性波形变换—滤波法。
ｉ延迟相乘法
当延迟时间等于码元持续时间一半时，可以得到最强的码元速率分量。
ｉ微分整流法
ｉｉ波形变换滤波法
ｉｖ开环同步的性能指标
若窄带滤波器的带宽等于１／ＫＴ，则提取同步的时间误差比例为
ε
－
Ｔ ＝ ０．３３
ＫＥｂ／ｎ槡 ０
　　
Ｅｂ
ｎ０
＞５， Ｋ１８
其中，ε
－
—同步误差时间的均值；Ｔ码元持续时间。
ｖ开环同步法的缺点
同步跟踪误差的均值不等于零，使信噪比增加可以降低跟踪误差。
１１０　
②闭环同步法—“超前／滞后门”同步器
将接收信号和本地产生的码元定时信号相比较，使本地产生的定时信息和接收码元的转变点保
持同步。超前门对应码元起始时间，滞后门对应码元结束时间。
（图见视频）
同步状态下，超前／滞后门的积分区间都全部在一个码元的持续时间内，积分器的积分结果相同，
误差电压为０，同步器达到稳定状态。误差电压ｅ＜０时，压控振荡器频率减小，使超前门受到延迟；误
差电压ｅ＞０时，压控振荡器频率增加，使滞后门提前。当超前和滞后门的积分区间等于码元持续时
间一半时，误差电压最大，此时压控振荡器可以得到最大的频率受控范围。
典型考研题３（西安电子科技大学２００９年）
在数字通信系统中，提取位同步的方法有哪些？对位同步信号的频率和相位的要求是什么？
答案：（１）数字通信系统中，提取载波同步的方法有两种：外同步法和自同步法，其中自同步法包
括开环码元同步法和闭环同步法。
（２）对位同步信号频率的要求是频率要等于接收信号的码元传码率，其相位要对准接收信号码元
的开始时间。
４．群（或帧）同步
（１）起止式同步法
（２）集中插入法
①巴克码
一个长为ｎ的码组 ｘ１，ｘ２，…，ｘ{ }
ｎ ，其中ｘｉ取值±１，其局部自相关函数
Ｒ（ｊ）＝∑
ｎ－ｊ
ｉ＝１
ｘｉｘｉ＋ｊ＝
ｎ
０，＋１，－{ １
当 ｊ＝０
当 ０＜ｊ＜ｎ
下面是{ }１１１００１１７位巴克码的自相关函数
樊昌信《通信原理》考研考点精讲
１１１　
②巴克码识别器
识别器输出波形
典型考研题（天津大学２００３年）
设数字传输系统中的帧同步码采用集中插入法，插入的同步码为７位巴克码，
（１）画出帧同步码识别器原理框图
（２）若输入二进制序列是０１０１１１１００１１１１００１００，（设各移位寄存器的初始状态均为零），画出帧同
步码识别器的各点波形（设判决门限电平为６）。
解：（１）帧同步码识别器原理框图
（２）帧同步码识别器各点波形
１１２　
③群同步系统的性能
群同步系统的性能指标主要有漏同步概率Ｐ１、假同步概率Ｐ２和同步平均建立时间ｔｓ。
设巴克码的长度为ｎ，每个码元出错的概率为ｐ，最大允许的出错的个数为ｍ。
ｉ漏同步概率Ｐ１
指同步系统将正确的同步位置漏过而没有捕捉到。漏同步的主要原因是噪声的影响，使正确的
同步码元变成错误的码元。
Ｐ１ ＝１－∑
ｍ
ｒ＝０
Ｃｒｎｐ
ｒ １( )－ｐｎ－ｒ
ｉ假同步概率Ｐ２
指当捕捉时同步系统将错误的同步位置当作正确的同步位置捕捉到。产生假同步的主要原因是
由于噪声的影响使信息码元错成同步码元。
Ｐ２ ＝
∑
ｍ
ｒ＝０
Ｃｒｎ
２ｎ
ｉｉ同步建立时间ｔｓ
ｔｓ≈ １＋Ｐ１＋Ｐ( )
２ ＮＴ
这里，Ｔ是码元宽度，Ｎ为每帧的码元数。
④群同步保护
群同步保护的目的是建立正确的群同步。接收端的群同步电路都有两种状态，即捕捉态和保持
态。捕捉态时，判决门限必须定的很高，以防止发生假同步，一旦确认达到同步状态，系统即转入保持
樊昌信《通信原理》考研考点精讲
１１３　
态。在保持态，为了防止由于噪声引起的个别错误导致认为失去同步，应该降低判决门限，防止漏
同步。
典型考研题１（西安电子科技大学２００３年）
设一数字传输系统采用的帧同步码组为７位长的巴克码（即１１１００１０）。采用连贯式插入法插入
帧同步码，系统的误码率为Ｐｅ。
（１）试求该巴克码的局部自相关函数Ｒ( )ｊ，并画出Ｒ( )ｊ与ｊ的关系；
（２）试画出帧同步信号识别器的原理框图；
（３）若识别器的判决电平设置在“允许至多有一位错码”的电平上，则该识别器的漏同步概率及
假同步概率如何？
解：（１）巴克码的自相关函数为
Ｒ（ｊ）＝∑
７－ｊ
ｉ＝１
ｘｉｘｉ＋ｊ＝
７，ｊ＝０
０或 ±１，
０，
{
ｊ＞ｎ
０＜ｊ＜ｎ
将巴克码{ }＋＋＋－－＋－代入得到
当ｊ＝０时，Ｒ( )０ ＝７
当ｊ＝１，３，５，７时，Ｒ( )ｊ＝０
当ｊ＝２，４，６时，Ｒ( )ｊ＝－１
（２）
（３）在群同步中，假同步的概率为
Ｐ＝２－ｎ∑
ｍ
ｒ＝０
Ｃｒｎ
其中，ｎ是巴克码的长度，ｍ是错码位数。由题知ｍ＝１，故假同步概率
１１４　
Ｐ＝２－７∑
１
ｒ＝０
Ｃｒ７ ＝２
－７ １＋( )７ ＝２－４ ＝
１
１６
漏同步概率
Ｐ＝１－∑
ｍ
ｒ＝０
ＣｒｎＰ
ｒ
ｅ １－Ｐ( )
ｅ
ｎ－ｒ＝１－ １－Ｐ( )
ｅ
７－７×Ｐｅ １－Ｐ( )
ｅ
６