概要信息：

Ch.5 晶体中电子在外场中的运动
1/110山西大学物电学院
固体物理学
Solid State Physics  
山西大学物电学院
第五章 晶体中电子
在电场和磁场中的运动
Chapter 5
Motion of Crystal Electrons
in Electric and Magnetic Fields
声明：本教案仅限课堂教学，未经许可禁止复制或它用。
Ch.5 晶体中电子在外场中的运动
2/110山西大学物电学院
引 言
上一章主要讨论了晶体中电子(Bloch电子)在晶格周期场中运动
的本征值和本征态，这是研究各种有关电子运动问题的基础。
本章将讨论晶体中电子在外场中的运动规律，这个外场可以
是电场、磁场、掺入晶体的杂质势场等。
一般外加的场(最大～104V/cm)比晶体周期场(～108V/cm)弱
得多，很自然可以想到：应以周期场中电子的本征态为基础，
来讨论晶体中电子在外场中的行为。讨论方法有：
①求解含有外场势U的Schrödinger方程：
②在一定条件下，晶体中的电子对外加电磁场的响应犹如一质量为
有效质量的经典粒子，这就是所谓的电子的准经典运动(用牛顿力学)。
条件：外场较弱、恒定，不考虑电子在不同能带间的跃迁，
不涉及电子的衍射和干涉等。
2
2 ( )2 V r U Em ψ ψ − ∇ + + =  
rh ( )V rr --晶体周期场
──通常是近似求解
Ch.5 晶体中电子在外场中的运动
3/110山西大学物电学院
主要内容
电子的准经典运动
恒定电场作用下晶体中电子的运动
导体、绝缘体和半导体的能带论解释
在恒定磁场中晶体中电子的运动
De Haas－Van Alphen效应*
Ch.5 晶体中电子在外场中的运动
4/110山西大学物电学院
①准经典运动，准经典运动的基本方程；
②有效质量近似，有效质量意义及其计算；
③晶体中电子在恒定电场中的运动图象(k空间与实空间)；
④导体、半导体和绝缘体的能带结构与导电性；
⑤空穴的概念，电子导电性与空穴导电性；
⑥晶体中电子在恒定磁场中的运动图象(k空间与实空间)、准
经典运动方程、垂直于磁场的平面内电子能量量子化；
⑦*了解电子回旋共振与De Haas-Van Alphen效应。
基本要求
第五章习题(共 4 题)：5.1~3，5.5。
( 去掉5.3，5.5题公式中的c )
Ch.5 晶体中电子在外场中的运动
5/110山西大学物电学院
建立电子准经典运动方程，需要电子的动量和坐标？
Ø矛盾：经典粒子和量子力学.
F对经典粒子，同时具有确定的动量和坐标；
F对电子，由测不准原理，同时具有确定的动量和坐标是
不可能的；
F怎么解决这个矛盾？
Ø晶体中电子的本征态用具有确定波矢k和能量的Bloch波
函数来描写，状态k完全确定，坐标完全不确定.
F然而，在外场下是非定态过程→k显然会发生变化;
F但在外场下电子状态可以看作是k附近的∆k范围内的本
征态迭加而成→波包(wave packet)→分布在r附近的∆r范围;
F波包坐标→电子的坐标！
§5.1 电子的准经典运动
Ch.5 晶体中电子在外场中的运动
6/110山西大学物电学院
& 对自由电子，波函数(单色平面波)：
一、波包与电子速度
( ) ikx
k x Aeψ =
2 2| ( ) | | |k x Aψ =在空间找到粒子的概率：
即粒子的位置是不确定的，而相应的动量却是确定的。
& 在一般情况下，可以把波函数ψk(x)看成是一个有许多单色波
叠加而成的波包，即以k0为中心的在∆k范围内各
种不同波矢 k 的单色平面波组成。
因而相应的动量也有一个分布，即电子没有
确定的速度。但平均速度是一定的，它相当于以
k0为中心的波包移动的速度──群速度。
——可以同时确定一个波包的中心位置和平均动量。
＝常量
1. 波包
|ψ|2
k0 k
∆k
为简单起见，先考虑一维情况，然后再推广到三维情况。
Ch.5 晶体中电子在外场中的运动
7/110山西大学物电学院
& 对晶体中的电子，是定域在某一范围∆x内──即在该区域找
到粒子的概率最大。如何用波函数描述定域空间的粒子呢？
Bloch波是调幅平面波，我们可像用de Broglie波构成波包描
述自由电子那样，用Bloch波构成波包描述晶体中电子的运动。
波包──在k0附近、∆k范围内，各种不同k、不同ω的Bloch
波的叠加。
假设∆k很小，即 2k π/a∆ <<
a为原胞的线度，则可认为周期性函数
0
( ) ( )k ku x u x≈
由于波包包含不同能量本征态，再考虑
到时间因子，把Bloch波写成：
( , )x tψ = ( )0 2
0 0 2
( )
k
k
k i kx t
k k
u x e dkω
∆
∆
+ −
−
≈ ∫
2. 电子的速度
( )0 2
0 2
( )
k
k
k i kx t
kk
e u x dkω
∆
∆
+ −
−∫
|ψ|2
k0 k
∆k
( ) ( ) /k E kω = h
Ch.5 晶体中电子在外场中的运动
8/110山西大学物电学院
则
令
( )0 2
0 0 2
( , ) ( )
k
k
k i kx t
k k
x t u x e dkωψ
∆
∆
+ −
−
= ∫ 令 0k k ξ= +
( )
0
0( )
k
d
dkk ωω ω ξ≈ +
( )0 0
0
( ) i k x t
ku x e ω−≈
( )0 0
0
( ) i k x t
ku x e ω−=
( )0 0
0
( ) i k x t
ku x e ω−=
( )
0k
d
dku x tω= −
相应的概率分布：
0
2
2 2 22
2
sin| ( , ) | | ( ) | ( )k
k
k
ux t u x k
u
∆
∆
ψ ∆
 
=  
 
( )
02
2
[ ]d
dk k
k
k
x ti
e d
ω∆
∆
ξ
ξ
−
−
⋅∫
22sin( )k u
u
∆
⋅
2
2
sin( )k
k
u k
u
∆
∆
⋅ ⋅ ∆
( )0 0
0
( ) i k x t
ku x e ω−=
2
2
1 ( )
k
k
uie d iuiu
∆
∆
ξ ξ
−
⋅ ∫
2 2
2
 
2 sin( )
k ki u i u
k
e e
i u
∆ ∆−
∆
−
=
Ch.5 晶体中电子在外场中的运动
9/110山西大学物电学院
k
2π
∆k
2π−
∆
2ψ
u0
( )
k
du x tdk
0
ω= − ，
0
2
2 2 22
2
sin| ( , ) | | ( ) | ( )k
k
k
ux t u x k
u
∆
∆
ψ ∆
 
=  
 
1)当u=0时，|ψ|2取最大值，
u=0处为波包中心，则
( )
0k
dx tdk
ω=
( ) ( )E k kω= h
( )
0
1
k
dE tdk= h
2)若将波包看成一个准粒子，则该粒子(波包中心)的速度为
0( ) dxk dt=v ( )
0
1
k
dE
dk= h
其中 而
即晶体中电子在k0态速度等于以k0为中心的波包移动的群
速度，并且其速度与电子能谱E(k)有关。
以a为周期，不会改变波包的形状。
→波包局域在晶体中某一区域内。
0
2| ( ) |ku x
三维
00
1( ) ( )k kk E= ∇v r r
rr
h
三维
0
1 ( )k kE t= ∇ r r
r
h
r
2a π/ k∆<<
2
2
2
sin k
k
u
u
∆
∆
Ch.5 晶体中电子在外场中的运动
10/110山西大学物电学院
由 |ψ|2=0，即 u k
2π= ± ∆
3) 波包宽度
对自由电子，
2 2
( ) 2
kE k m= h
( ) kk m=v h 0
0
1( )
k
dEk dk
 =  
 
v h
则
k usin 0,2
∆ = k u ,2
∆ π= ±
主波包范围： u  k k
2 2π π ∈ − ∆ ∆ 
， 主波包宽度： u k
4π∆ =
∆
2π k
a
∆ <<∵ ，
4 u a
k
π
∴ ∆ = >>
∆
即波包线度远大于原胞线度。因此
在实际问题中，只能在这个限度内
把电子看作一个准经典粒子。
0
2
2 2 22
2
sin| ( , ) | | ( ) | ( )k
k
k
ux t u x k
u
∆
∆
ψ ∆
 
=  
 
k
2π
∆k
2π−
∆
2ψ
u0
Ch.5 晶体中电子在外场中的运动
11/110山西大学物电学院
例如在输运过程中，只有当自由程远大于原胞的情况下，
才可以把电子看作一个准经典粒子。
晶体中电子运动的准经典模型：
外场用经典方式处理，晶体周期场用能带论处理，电子位
置用Bloch波包的中心位置代替，且Bloch电子的速度用Bloch
波包的群速度来代替，即
0
0
1( )
k
dEk dk
 =  
 
v h
00
1( ) ( )k kk E= ∇v r r
rr
h
(一维)
(三维)
Ch.5 晶体中电子在外场中的运动
12/110山西大学物电学院
二、在外力作用下状态的变化和准动量
F dt dE=v
考虑一维情况。电子在外场中所受的力为F，在dt 时间
内，电子获得的能量 dE 就等于外场对电子所做的功Fvdt，即
1 dE
dk
 =  
 
v h1F dE
dt= v
1 dE dk
dk dt= v
dk
dt= h ( )d
dt
k
=
h
其中 取代了经典力学中的动量。
准经典运动中及其它一些方面， 具有类似于动量的性质，
但不是Bloch电子真实的动量(因Bloch波并不对应于确定的动量，
即不是动量的本征态)，因此常称为晶体中电子的准(赝)动量。
kh
kh
此式表示晶体中电子在外力作用下运动状态变化的基本公式。
在经典情况，动量变化率等于作用在电子上所有力的矢量
和，而准动量变化率只是外场作用结果，这里没有包括晶格势
场的作用力，晶格势场的作用包含在准动量(即E(k))中。
Ch.5 晶体中电子在外场中的运动
13/110山西大学物电学院
三、晶体中电子的加速度和有效质量
晶体中电子准经典运动的基本关系式：
( )d kF
dt
=
h1( ) dEk dk
 =  
 
v h
由此可直接导出在外力 F作用下晶体中电子的加速度：
a d
dt= v 1d dE
dt dk
 = ⋅ 
 h
2
2
1 dk d E
dt dk
= ⋅
h
1 d dE dk
dk dk dt
 = ⋅ ⋅ 
 h
2
2 2
)1 (d k
d kt
d E
d
= ⋅
h
h
2
2 2
1 dF E
dk
= ⋅
h
与经典牛顿定律 a = F/m 比较，引入晶体中电子的有效质量：
12
2
2
d E
dk
−
 =  
 
h
12
2 2* 1 d E
dk
m
−
 =  
 h
*
F
m=
(一维)
Ch.5 晶体中电子在外场中的运动
14/110山西大学物电学院
12
2 2* 1 d E
dk
m
−
 
=  
 h
12
2
2 ,d E
dk
−
 
=  
 
h
对自由电子，
2 2
( ) 2
kE k m= h ， .*m m=则
在近自由电子近似中，在 处发生Bragg全反射，
导致禁带的出现。
0
nk a
π=
事实上，当波矢
的反射波存在，两者相互作用产生两个能带：
0 (1 )k k ∆′ = +
( ∆ << 1)0(1 )k k ∆= − −
的波在晶体中前进时，必有波矢
显然，m*也与电子能谱有关。周期性势场中电子在外场中的运
动，就好象质量为m*的经典带电粒子在外场中的运动。
有效质量的作用在于它概括了晶体内部周期场作用(把这个
作用用有效质量代替)，使我们能够简单地由外场力确定电子的
加速度，而不必考虑晶体周期场的作用力。
*
Fa m=
Ch.5 晶体中电子在外场中的运动
15/110山西大学物电学院
22
| | 1| |
n
n n n
n
TE T V T V+
 = + + + ∆ 
 
22
| | 1| |
n
n n n
n
T
E T V T V−
 = − − − ∆ 
 
2 2
0
2n
kT m=
h
0
1k
k∆ = +
0 (1 )k k ∆= − −
E
E－
E＋
0k k
d Em
dk
12
2 2
1*
−
 =  
 h ( )d E d
dkd
122
2 2
1
−
 ∆=  ∆ h
d E
k d
12
2 2 2
0
1
−
 
=  ∆ h
则在上能带 E+ 的底部电子的有效质量为：
1
2 2
0
21 2 1
| |
n
n
n
T
T
k V
m
−
∗
  
= ⋅ +  
   h底
1
2
1
| |
n
n
T
m
V
−
 
= + 
 
同理在下能带 E－的顶部电子的有效质量为：
1
2 2
0
21 2( ) 1
| |
n
n
n
T
T
k V
m∗
−
  
= ⋅ − −  
   h顶
1
2
1
| |
n
n
T
m
V
−
 
= − − 
 
> 0
< 0
Ch.5 晶体中电子在外场中的运动
16/110山西大学物电学院
有效质量 m*的物理意义：
1) 在同一能带中，m*不是常量，m*低>0，m*顶<0 。
m*不是电子的惯性质量，它体现了晶格周期场的影响，
这种影响主要通过Bragg反射的形式，在电子和晶格(声子)之
间交换动量。
设晶体中的电子除受外场作用力F的作用外，还受晶格作
用力为FL，则
说明
LF F
a m
+
= *
Fa m=
这就是说，电子的有效质量m*体现了晶格的作用。而且
*
LFdt F dtFdt
m m
+
=
FL 难以求出，改写为
冲量→动量的增量
( ) 1 [( ) ( ) ]*
p
p pm m
∆
= ∆ + ∆赋予
赋
外场 电子的
外场 电子的 晶格赋予电子的予
Ch.5 晶体中电子在外场中的运动
17/110山西大学物电学院
( ) 1 [( ) ( ) ]*
p
p pm m
∆
= ∆ − ∆赋予
赋
外场 电子的
外场 电子的 电子赋予晶格的予
处于外场中的Bloch电子，一方面从外场获得动量，另一
方面赋予晶格(声子)动量，当电子
从外场获得的动量 > 交给声子的动量，m*>0 ；
从外场获得的动量 < 交给声子的动量，m*<0 ；
从外场获得的动量 = 交给声子的动量，m*= ∞。
可见，晶体中电子的m*可正可负，甚至可以是无穷大。
2) 晶体中质量为m的电子，在外场中的行为犹如质量为m*
的自由电子，只要赋予晶体中电子以质量m*，就可用经典力
学描述其运动——有效质量近似(Effective mass approximation)。
处于能带底部电子，好似具有质量m*底的自由电子运动；
处于能带顶部电子，好似具有质量m*顶的自由电子运动。
Ch.5 晶体中电子在外场中的运动
18/110山西大学物电学院
四、近自由电子 v、 m*与 k 的关系曲线
1. 晶体中电子的速度
1 dE
dk
 =  
 
v hu E(−k) =E(k)，
( )1( )
( )
dE kk d k
−
− =
−
v h
1 ( )dE k
dk
= −
h
( )k= −v
0dE
dk
=
在能带底和能带顶，电子速度v＝0。
u在能带底和能带顶，E(k)取极值，
2
2 0,d E
dk
=u在能量拐点，
电子速度的数值最大。
与自由电子的速度总是随能量的增
加而单调上升，是完全不同的:
E
a
π
−
a
π
ck
v
0
k
0
k
0d
dk =v
2 2
( )
2
kE k
m
=
h
， ( ) kk m= hv
自由电子
Ch.5 晶体中电子在外场中的运动
19/110山西大学物电学院
v
0
k
2. 晶体中电子的有效质量
12
2
2* d Em
dk
−
 
=  
 
h
1 dE
dk
 =  
 
v h1d
dk
−
 =  
 
vh
1
1d dE
dk dk
−
  =     
h
h
2
2 0,d E
dk
=u在能量拐点， 0,d
dk =v
 ;*m∴ → ∞
u在能带底附近，E取极小值，
2
2 0,d E
dk
>
 0 ; m∗∴ >
低
u在能带顶附近，E取极大值，
2
2 0,d E
dk
<
 0.m∗∴ <
顶
u当k越过能量拐点时，m*改变符号。
u在 处，m*取极值。
2
2 0d
dk
=v
*( ) * ( )m k m k− =
E
a
π
−
a
π
ck0
k
*m
0
k
Ch.5 晶体中电子在外场中的运动
20/110山西大学物电学院
1( ) ( )kk E= ∇v r
rr
h
类似于一维情况，可写出三维晶体中的电子速度、电子
准动量、电子加速度和电子的有效质量。
1. 电子速度公式
ky
kx0
1
x
x
E
k
 ∂=  ∂ 
v h
1
y
y
E
k
 ∂=  ∂ 
v h
1
z
z
E
k
 ∂=  ∂ 
v h
五、三维情况
( ) ( ) .k E k k⊥v v v
r r rr r r
与 的 成正比， ，但 不一定能面 平行梯度 等
vr
k
r
等能面
只有当等能面为球面，或在某些特殊方向上， .// kv
rr
Ch.5 晶体中电子在外场中的运动
21/110山西大学物电学院
晶体中电子的
准动量为： p k=
rr h( )F kd
dt
=
r
hr
2. 外力作用下运动状态变化的基本公式和准动量
3. 晶体中电子的加速度和有效质量公式
da dt= vrr
1( ) ( )kk E= ∇v r
rr
h
1 ( )k
d
dt
E∇= r
h
2
1 ( )k k Ea F = ∇ ∇ ⋅ 
 
r r
h
rr
1 ( )k k E dk
dt
∇= ∇ ⋅r r
h
r
2
1 ( ( ))k k E d
dt
k
∇ ∇ ⋅= r r
r
h
h
1
2
1* ( )k km E
−
 = ∇ ∇ 
 
r r
h
──二阶张量(并矢)
──有效质量张量
1
* Fm= ⋅
r
─倒有效质量张量
1
*m
其中：
( ) ( ) ( )
( ) y zxk k k
k
x y z
dk dkdE Ekd
dt k dt k dt k dt
E
E
∇ ∇∂ ∂ ∂
= + +
∂ ∂ ∂
∇
∇
r r r
r
Ch.5 晶体中电子在外场中的运动
22/110山西大学物电学院
分量形式： 1x
x
x
d d Ea dt dt k
 ∂= =  ∂ h
v
2
2
1 Ea Fk kα β
β α β
∂=
∂ ∂∑h α , β = x, y, z 
1 y zx
x x y x z x
dk dkdkE E E
k k dt k k dt k k dt
      ∂ ∂ ∂ ∂ ∂ ∂= + +      ∂ ∂ ∂ ∂ ∂ ∂      h
矩阵形式： 2 2 2
2
2 2 2
2 2
2 2 2
2
1
x y x zx
x x
y y
y x y zy
z z
z x z y z
E E E
k k k kk
a F
E E Ea Fk k k kk
a F
E E E
k k k k k
 ∂ ∂ ∂
 ∂ ∂ ∂ ∂∂        ∂ ∂ ∂=     ∂ ∂ ∂ ∂∂    
    ∂ ∂ ∂ 
∂ ∂ ∂ ∂ ∂  
h
注意 电子的加速度方向并不一定与外力的方向一致，这
是由倒有效质量张量的性质所决定的。
2 2 2
2 2
1
x y z
x y x zx
E E EF F Fk k k kk
 ∂ ∂ ∂= + + ∂ ∂ ∂ ∂∂ h
2
1
k
x
E
k F ∂= ∇ ⋅ ∂ 
r
r
h
2
1
k
E
k F
α
 ∂= ∇ ⋅ ∂ 
r
r
h
Ch.5 晶体中电子在外场中的运动
23/110山西大学物电学院
2 2 2
2
2 2 2
2 2
2 2 2
2
1 1
x y x zx
y x y zy
z x z y z
E E E
k k k kk
E E E
k k k km k
E E E
k k k k k
∗
 ∂ ∂ ∂
 ∂ ∂ ∂ ∂∂ 
 ∂ ∂ ∂  =    ∂ ∂ ∂ ∂  ∂ 
 ∂ ∂ ∂ 
∂ ∂ ∂ ∂ ∂  
h
倒有效质量张量的矩阵形式：
2
2
1 1 E
m k kαβ α β
∗
∂
=
∂ ∂h
倒有效质量张量的分量形式：
由于微商可以交换顺序，倒有效质量张量是对称张量。
若将kx、ky、kz取为张量的主轴方向，可将其对角化。
α , β = x, y, z 
Ch.5 晶体中电子在外场中的运动
24/110山西大学物电学院
当 时，m*退化为一个标量,
若选kx,ky,kz轴沿张量主轴方向，则有：
2 0
0
E
k kα β
α β
α β
≠ =∂
∂ ∂ = ≠
，
，
这时倒有效质量张量是对角化的。
2
2
1 1 E
m k kαβ α β
∗
∂
=
∂ ∂h
2
2
2
2 2
2
2
0 0
1 1 0 0
0 0
x
y
z
E
k
E
m k
E
k
∗
 ∂ 
∂ 
 ∂  =    ∂   
 ∂ 
∂  
h
1 ,x x
x
a F
m∗= 1 ,y y
y
a F
m∗= 1
z z
z
a F
m∗=
1 0 0
10 0
10 0
x
y
z
m
m
m
∗
∗
∗
 
 
 
 
=  
 
 
 
  
一般来说，mx*、my*、mz*不一定相等，所以加速度
和外力方向可以不同。
x y zm m m m∗ ∗ ∗ ∗= = = 1
*a Fm=
rr
Ch.5 晶体中电子在外场中的运动
25/110山西大学物电学院
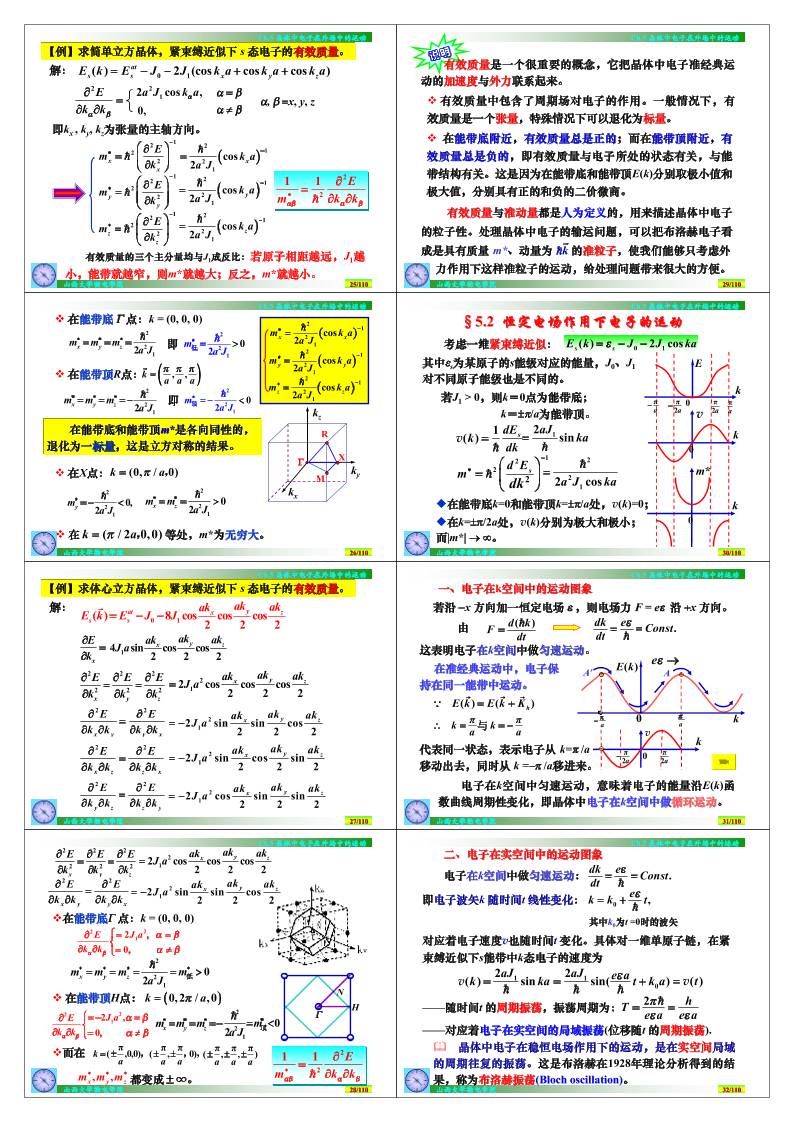
【例】求简单立方晶体，紧束缚近似下 s 态电子的有效质量。
0 1( ) 2 (cos cos cos )at
s s x y zE k E J J k a k a k a= − − + +
2E
k kα β
∂
=
∂ ∂
α = β
α ≠ β
α, β =x, y, z
即kx , ky, kz为张量的主轴方向。
x
x
Em
k
12
2
2
−
∗  ∂
=  ∂ 
h
a J k a2
12 cos ,α
0,
( )
2
1
2
1
cos
2 xk a
a J
−
=
h
y
y
Em
k
1
2
2
2
−
∗
 ∂
=   ∂ 
h ( )
2 1
2
1
cos
2 yk a
a J
−
=
h
z
z
Em
k
12
2
2
−
∗  ∂
=  
∂ 
h ( )
2
1
2
1
cos
2 zk a
a J
−
=
h
有效质量的三个主分量均与J1成反比：若原子相距越远，J1越
小，能带就越窄，则m*就越大；反之，m*就越小。
解：
2
2
1 1 E
m k kαβ α β
∗
∂
=
∂ ∂h
Ch.5 晶体中电子在外场中的运动
26/110山西大学物电学院
v在能带底 Γ点：k = (0, 0, 0)
x y zm m m
a J
2
2
12
∗ ∗ ∗= = = h
v在能带顶R点： ( )k a a a, ,π π π=
r
x y zm m m
a J
2
2
12
∗ ∗ ∗= = = − h
在能带底和能带顶m*是各向同性的，
退化为一标量，这是立方对称的结果。
( )x xm k a
a J
2
1
2
1
cos
2
−∗ = h
( )y ym k a
a J
2 1
2
1
cos
2
−∗ = h
( )z zm k a
a J
2
1
2
1
cos
2
−∗ = h
ky
kx
kz
M
X
R
Γ
v在X点： (0, / 0)k aπ= ，
ym
a J
2
2
1
0,
2
∗ = − <
h
x zm m
a J
2
2
1
0
2
∗ ∗= = >
h
m
a J
2
2
12
0∗ <= −
h
顶
v在 等处，m*为无穷大。( / 2 0,0)k aπ= ，
m
a J
2
2
12
0∗ >= h
低即
即
Ch.5 晶体中电子在外场中的运动
27/110山西大学物电学院
【例】求体心立方晶体，紧束缚近似下 s 态电子的有效质量。
解：
0 1( ) 8 cos cos cos
2 2 2
yat zx
s s
ak akak
E k E J J= − −
v
2 2
x y y x
E E
k k k k
∂ ∂
=
∂ ∂ ∂ ∂
2 2 2
2 2 2
x y z
E E E
k k k
∂ ∂ ∂
= =
∂ ∂ ∂
2 2
y z z y
E E
k k k k
∂ ∂
=
∂ ∂ ∂ ∂
2 2
x z z x
E E
k k k k
∂ ∂
=
∂ ∂ ∂ ∂
x
E
k
∂
=
∂ 14 sin cos cos
2 2 2
y zx ak akak
J a
2
12 cos cos cos
2 2 2
y zx ak akak
J a=
2
12 sin sin cos
2 2 2
y zx
ak akak
J a= −
2
12 sin cos sin
2 2 2
y zx
ak akak
J a= −
2
12 cos sin sin
2 2 2
y zx
ak akakJ a= −
Ch.5 晶体中电子在外场中的运动
28/110山西大学物电学院
2 2 2
2 2 2
x y z
E E E
k k k
∂ ∂ ∂
= =
∂ ∂ ∂
2
12 cos cos cos
2 2 2
y zx
ak akakJ a=
2 2
x y y x
E E
k k k k
∂ ∂
=
∂ ∂ ∂ ∂
v在能带底Γ点：k = (0, 0, 0)
Γ
H
N
22
12
0  
J aE
k kα β
α β
α β
 = =∂

∂ ∂ = ≠
，
，
x y zm m m
a J
2
2
12
∗ ∗ ∗= = =
h m 0∗= >低
v在能带顶H点： ( )0, 2 / ,0k aπ=
2
2
12x y zm m m
a J
∗ ∗ ∗= = =−
h m 0∗= <
顶
v而在 π( ,0,0)k
a
= ± ，
x y zm m m, ,∗ ∗ ∗都变成±∞。
π π( ,  0)
a a
± ± ， ， π π π( , , )
a a a
± ± ±
2
12 sin sin cos
2 2 2
y zx ak akak
J a= −
2
2
1 1 E
m k kαβ α β
∗
∂
=
∂ ∂h
22
12 ,
0  
J aE
k kα β
α β
α β
= − =∂

∂ ∂ = ≠ ，
Ch.5 晶体中电子在外场中的运动
29/110山西大学物电学院
说明
v 在能带底附近，有效质量总是正的；而在能带顶附近，有
效质量总是负的，即有效质量与电子所处的状态有关，与能
带结构有关。这是因为在能带底和能带顶E(k)分别取极小值和
极大值，分别具有正的和负的二价微商。
有效质量是一个很重要的概念，它把晶体中电子准经典运
动的加速度与外力联系起来。
v有效质量中包含了周期场对电子的作用。一般情况下，有
效质量是一个张量，特殊情况下可以退化为标量。
有效质量与准动量都是人为定义的，用来描述晶体中电子
的粒子性。处理晶体中电子的输运问题，可以把布洛赫电子看
成是具有质量 m*、动量为 的准粒子，使我们能够只考虑外
力作用下这样准粒子的运动，给处理问题带来很大的方便。
k
r
h
Ch.5 晶体中电子在外场中的运动
30/110山西大学物电学院
§5.2 恒定电场作用下电子的运动
考虑一维紧束缚近似： 0 1( ) 2 coss sE k J J kaε= − −
其中εs为某原子的s能级对应的能量，J0、J1
对不同原子能级也是不同的。
若J1 > 0，则k＝0点为能带底；
k＝±π/a为能带顶。
1( ) sdE
k
dk
=
h
v
12
2
2
sd E
m
dk
−
∗  
=  
 
h
12 sinaJ ka=
h
2
2
12 cosa J ka
=
h
u在k=±π/2a处，v(k)分别为极大和极小；
而|m*| → ∞。
u在能带底k=0和能带顶k=±π/a处，v(k)=0；
E
v
0
k
0
k
*m
0
k
π
2a− π
2a
π
a− π
a
Ch.5 晶体中电子在外场中的运动
31/110山西大学物电学院
v
a
π− a
π
一、电子在k空间中的运动图象
若沿 −x 方向加一恒定电场 ε，则电场力 F = eε 沿 +x 方向。
由
这表明电子在k空间中做匀速运动。
d kF dt
( )= h dk e
dt
ε= h
eε →
AA’
h E k E k K( ) ( )= +
r r r
∵
π π k ka a∴ = = −与
代表同一状态，表示电子从 k=π /a
移动出去，同时从 k =−π /a移进来。
电子在k空间中匀速运动，意味着电子的能量沿E(k)函
数曲线周期性变化，即晶体中电子在k空间中做循环运动。
0
k
π
2a− π
2a
在准经典运动中，电子保
持在同一能带中运动。
.Const=
0 k
( )E k
Ch.5 晶体中电子在外场中的运动
32/110山西大学物电学院
dk e Constdt .ε= =h
即电子波矢k 随时间t 线性变化： 0 ,ek k tε= + h
其中k0为t =0时的波矢
对应着电子速度v也随时间t变化。具体对一维单原子链，在紧
束缚近似下s能带中k态电子的速度为
12( ) sinaJk ka=v h
1
0
2 sin( )aJ e a t k aε= +h h ( )t= v
——随时间t 的周期振荡，振荡周期为：
——对应着电子在实空间的局域振荡(位移随t 的周期振荡).
2 hT e a e a
π
ε ε
= =h
& 晶体中电子在稳恒电场作用下的运动，是在实空间局域
的周期往复的振荡。这是布洛赫在1928年理论分析得到的结
果，称为布洛赫振荡(Bloch oscillation)。
电子在k空间中做匀速运动：
二、电子在实空间中的运动图象
Ch.5 晶体中电子在外场中的运动
33/110山西大学物电学院
E
a
π
−
a
π
v
0
k
0
k
*m
0
k
π
2a
−
π
2a
F eε= → v随时间作周期性振荡图象：
假设 t=0时，电子处在带低k=0，
m*>0，外力作用使电子加速；
当k=π/2a时，m*→∞，速度极大；
k＞π/2a，m*<0，开始减速，直至
k=π/a时速度v=0；
这时电子处在带顶，m*<0，外力
作用继续使v<0；
当k在-π/a至-π/2a之间时，v绝对值
不断增大，至-π/2a时达到极小值；
当k＞-π/2a，m*>0，开始加速，使
速度绝对值减小，当k=0时，v=0.
*
Fa m=
实质：晶格周期场作用，使电子在
布里渊区边界受到Bragg反射的结果。
Ch.5 晶体中电子在外场中的运动
34/110山西大学物电学院
x
电子速度的周期性振荡，即电子在实空间中的周期性振荡。
恒定外电场ε(沿−x方向)的存在,电势V=ε x(沿x轴增大)，附加电势
能−eV(沿x轴减小)，电子总能量随x变化，能带发生倾斜。
E
x
无外场ε=0 −eV
x
E
x
ε ≠0能带倾斜
斜率为-eε
A  B  C 带隙
下能带 上能带
ACA →→ 为一周期T
π0A C a→ →，相当于从
π 0C A a→ − →，相当于从
经典近似中，电子局限在同
一能带(较低能带)中运动，遇到势
垒(带隙)将全部反射回来。
T =
简约区宽度
电子在k空间速度
Ch.5 晶体中电子在外场中的运动
35/110山西大学物电学院
说明
(1)电子受晶体中杂质、缺陷及声子散射(碰撞)作用，两次散
射间电子在k空间移动的距离与布里渊区尺度相比甚小，电子来
不及完成振荡运动就被散射破坏掉了。
相邻两次散射间的平均时间间隔τ (电子平均自由运动时间)
很小，电子还来不及完成一次振荡过程就已被散射。
实空间中电子的振荡运动很难观察到：
在晶体中，τ：10−12 ∼10−13 s，a ≈ 3×10−10 m
为了观察到电子振荡的全过程，至少要求 τ = T。
u对金属：无法实现高电场；
对绝缘体：将被击穿──电击穿(electric breakdown)。
满足要求所需加的电场 ε：105 ∼ 106 V/cm。
电子振荡周期： dk e
dt
ε=h2 2a
e e a
π π
ε ε= = h
h
T =
简约区宽度
电子在k空间速度
Ch.5 晶体中电子在外场中的运动
36/110山西大学物电学院
带隙
d
Eg
(2)按照量子力学，电子遇到势垒时将有部分穿透势垒(隧
道效应)，部分被反射回来。
电子穿透势垒的概率与势垒的高度(即能隙Eg)和势垒的
长度(d=Eg/eε，由外场决定)有关。
2
exp 2g
g
E
Em
e
ε
ε
π  
∝ −  
  h
概穿透 率
能隙Eg越宽，穿透概率越小；但随电场ε增大，穿透概率
急剧增加；当电场足够强时，若下面的能带被电子填充满，
或者接近填充满，上面能带是空带可以接纳电子，下面能带
中的电子有一定的概率穿透带隙而到达上面的能带(导带) 
──隧道效应。
x
下能带 上能带
E
θ
tan gE
edθ ε=∼
Ch.5 晶体中电子在外场中的运动
37/110山西大学物电学院
§5.3 导体、绝缘体和半导体的能带论解释
自然界的各种物质，根据其导电能力的差别，可分为：
导 体──电阻率 ρ <  10-4 Ω⋅cm 
绝缘体──电阻率 ρ >  109 Ω⋅cm
半导体──电阻率 ρ介于 10-4 ～109 Ω⋅cm
特鲁德的经典理论，提出金属导电的电子数等于原子价电
子数的假设，在处理金属导电性问题上是相当成功的，而其它
一些固体的导电性却得不到解释。
问题的提出：所有晶体都包含大量的电子，但电子的导电
性为什么却相差非常大？
导体、半导体和绝缘体的区别到底在哪里？
能带论的一个重要贡献，就是成功解释了为什么有些晶体
是导体，有些却是绝缘体或半导体。
Ch.5 晶体中电子在外场中的运动
38/110山西大学物电学院
晶体中电子的能量本征值分裂成一系列能带，每个能带均
由N个准连续的能态组成(N为晶体原胞数)，所以每个能带可容
纳2N个电子。
晶体中电子服从泡利不相容原理和能量最小原理，从最低
能带中的最低能级开始填充，依次占据能带中的各个能级。
满带(filled band)──被电子填满的能带；
空带(empty band)──未被电子填充的能带。
导带(conduction band)──最低空带或被电子部分填充的能带；
价带(valence band)──被价电子填充的能带；
近满带(nearly-filled bands)──一个能带的绝大部分能
态已填有电子，只有少数能级是空的能带。
带隙(band gap)──价带顶与导带低之间的能量范围。
Ch.5 晶体中电子在外场中的运动
39/110山西大学物电学院
即电子占据 态与 态的概率相等──电子对称分布，
则无宏观电流，
k
r
k−
r
一、晶体中产生电流的条件
由于 ，即波矢为 的状态与波矢为 状态
中电子速度是大小相等、方向相反的。若 态与 态中电子
分布相同，则无宏观电流 。
( ) ( )v k v k= − −
r rr r k−
r
k
r
k
r
k−
r
0I =
1. 无外电场
电子占据 态的概率为k
r
[ ( ) ]
1( ( )) ( )
1F BE k E k T
f E k f k
e −
= =
+
r
r r
 ( ) ( )E k E k= −
r r
∵  ( ) ( )f k f k∴ = −
r r
晶体中的电流，是电荷定向运动形成的。
0.I =
0ε =
r v
0
k
π
a− π
a
Ch.5 晶体中电子在外场中的运动
40/110山西大学物电学院
v
0
k
0
k
E
v
0
k
0
k
E
1)满带情况 2)非满带情况
结论：无论满带、非满带情况，
电子对称分布，电子电流互相抵
消，晶体中无宏观电流。
0ε = 时,
非满带
满带
0I =
Ch.5 晶体中电子在外场中的运动
41/110山西大学物电学院
v
2. 有外电场 0ε ≠
r
,F eε= −
r r
电子受力： ( ) ,d k edt ε= −
r
rh dk e
dt ε= −
r
r
h
即所有状态代表点都以相同速度，逆电场方向移动。
1) 满带情况：所有状态代表点逆电
场方向移动，由FBZ一边出去的电子，
在另一边同时填充进来，保持整个能带
处于均匀填满的状态，不产生电流。
2) 非满带情况：整个电子分布逆电
场方向移动，破坏了原来的对称分布，
而有一个小的偏移。电子电流只是部分
抵消，因而产生一定电流。
0
k
0
k
Eε←
r
满带电子不导电；非满带电子在外场
作用下可以导电，则非满带称为导带。
0≠ε 时,
导带
满带
0≠I
0I =
0
k
E ε←
r
Ch.5 晶体中电子在外场中的运动
42/110山西大学物电学院
二、导体、绝缘体和半导体的能带模型
Ch.5 晶体中电子在外场中的运动
43/110山西大学物电学院
非满带
T≠0K
当原子组成晶体时，能级过渡成能带。
导体
导
带
半导体绝缘体
禁
带
空带
禁带宽能带无重叠
E
能带重叠
非满带
禁带
禁带窄
空带
T=0K
禁带
1.导体：碱金属，如Na： 1622 3s2p2s1s ，3s电子只占一半能带。
碱土金属，如Mg： 2622 3s2p2s1s ，能带重叠，出现不满带。
2.绝缘体：禁带宽度一般都较宽， Eg >5eV。
如金刚石：Eg~5.5eV；α-Al2O3：Eg~ 8eV；NaCl：Eg~6 eV。
3.半导体：禁带宽度一般较窄：Eg介于0.2 ~ 3.5 eV之间 .
常规半导体：
Si: Eg ~1.1eV
Ge: Eg~0.7eV
GaAs:Eg~1.5eV
宽带隙半导体：
β-SiC: Eg~2.3eV
ZnO: Eg~3.4eV
TiO2: Eg~3.0eV
热激发
价带 价带满带 满带
二
价
金
属
Ch.5 晶体中电子在外场中的运动
44/110山西大学物电学院
利用材料模拟软件Materials Studio中的 CASTEP
模块计算的碱金属Na晶体(bcc)的能带和分波能态密度
2s
2p
3s
Γ Γ
11Na: 2s2 2p6 3s1
返
回
EF
3p
2s
2p
Ch.5 晶体中电子在外场中的运动
45/110山西大学物电学院
利用材料模拟计算软件Materials Studio中的 CASTEP
模块计算的碱土金属Mg晶体(hcp)的能带和分波能态密度
Γ Γ
12Mg：2p6 3s2
2p
3s
返
回
3p
EF
2p
Ch.5 晶体中电子在外场中的运动
46/110山西大学物电学院
利用材料模拟计算软件Materials Studio中的 CASTEP
模块计算的半导体Si晶体(diamond)的能带和分波能态密度
Γ
14Si：3s2 3p2
3sp3杂化
3s
3pz
3px,py
返
回
价带顶
导带底
禁带
间接带隙半导体
价
带
导
带
3s
3p
3p3s
Ch.5 晶体中电子在外场中的运动
47/110山西大学物电学院
利用材料模拟计算软件Materials Studio中的 CASTEP
模块计算的半导体GaAs晶体(fcc)的能带和分波能态密度
Γ
31Ga: 3d10 4s2 4p1
33As：4s2 4p3
Ga 3d
As 4s
As 4s4p
Ga 4s4p价带顶
导带底
禁带
直接带隙半导体
返
回
4sp3杂化
带隙
Ch.5 晶体中电子在外场中的运动
48/110山西大学物电学院
对化合物类绝缘体，如：NaCl晶体。
Na：1s22s22p63s1；Cl：1s22s22p63s23p5。
Na与Cl结合成NaCl晶体时，Na的3s带比Cl的3p带高约6eV，在Cl
的3p带中可以填充6N个电子，但N个Cl原子中只有5N个3p电子，于是
在能量较高的Na的3s带中的N个电子就转移到能量较低的Cl的3p带
中，刚好填满Cl的3p带，而Na的3s带成为空带，其能隙Eg~6eV，所
以NaCl晶体为绝缘体。
对第IIIA族元素类似碱金属的情况，只不过这时形成导带的是np
电子，而不是ns电子。如Al：3s23p1，Ga：4s24p1。所以第III族元素
的晶体绝大多数为金属。
周期表中第IVA族及其以上的元素，由于其电子态和结合形式比
较复杂，所以必须经过具体计算之后，才能判断是金属还是非金属。
例如金刚石是绝缘体，石墨是导体，而Si和Ge是典型的半导体。
过渡族元素都含有未满的 d 壳层，表现出金属性。原子 d 轨道5重
简并，使得形成的 d 能带能态密度特别大，且与 s 能带在很大程度上
重叠，费米能级位于 d 能带中。如Fe、Cu。
再如α-Al2O3晶体。
Ch.5 晶体中电子在外场中的运动
49/110山西大学物电学院
利用材料模拟计算软件Materials Studio中的 CASTEP
模块计算的第III族元素碱金属Al晶体(fcc)的能带和分波能态密度
13Al：3s2 3p1
3p
3s
返
回
Γ
EF
KW
Ch.5 晶体中电子在外场中的运动
50/110山西大学物电学院
利用材料模拟计算软件Materials Studio中的 CASTEP
模块计算的过渡族元素Fe晶体(bcc)的能带和分波能态密度
26Fe：3d64s2
3d
4s
返
回
Γ Γ
Ch.5 晶体中电子在外场中的运动
51/110山西大学物电学院
利用材料模拟计算软件Materials Studio中的 CASTEP
模块计算的过渡族元素Cu晶体(fcc)的能带和分波能态密度
29Cu：3d104s1
3d
4s
返
回
Γ
Ch.5 晶体中电子在外场中的运动
52/110山西大学物电学院
利用材料模拟计算软件Materials Studio中的 CASTEP
模块计算的绝缘体NaCl晶体(fcc)的能带和分波能态密度
Γ
11Na：2s2 2p6 3s1
17Cl：3s2 3p5
Na 2s
Na 2p
Na 3s
Cl 3p
Cl 3s
返
回
禁带
价
带
导
带
Ch.5 晶体中电子在外场中的运动
53/110山西大学物电学院
利用材料模拟计算软件Materials Studio中的 CASTEP
模块计算的绝缘体α-Al2O3晶体(rhomb)的能带和分波能态密度
13Al：3s2 3p1
8O：2s2 2p4
O 2s
返
回
O 2p
Al 3s Al 3p
Γ
禁带
价
带
导
带
Ch.5 晶体中电子在外场中的运动
54/110山西大学物电学院
【问】在低温下氢可以结晶为分子形态，也可以得到周期性排列
的单原子形态氢的亚稳态薄膜．试解释为什么分子形态的晶体氢
是绝缘体，而单原子形态的氢薄膜却具有金属的性质？
【答】分子形态的氢，每个原胞有两个价电子，能带为满带，所
以分子形态的晶体氢是绝缘体；
单原子形态氢的亚稳态薄膜，每个原胞有一个价电子，能
带为半满带，所以单原子形态的氢薄膜具有金属的性质。
Ch.5 晶体中电子在外场中的运动
55/110山西大学物电学院
4. 半金属──介于金属与半导体之间的中间状态。
u V族元素As(砷,4p3)、Sb(锑,5p3)、Bi(铋,6p3)，具有三角晶格结构；每
个原胞包含两个原子，则每个原胞含有偶数个价电子，似乎应是非导体; 
u导电性——导带底和价带顶发生交叠或具有相同能量;
u导电能力远小于金属——能带交叠较少，对导电有贡献的载流
子数远远小于普通的金属.
u导带中电子密度比普通金属小几个数量级：
As: 2.1×1020cm-3;  Sb: 5.7 ×1019cm-3; 
Bi:  2.7×1017cm-3
金属Cu：8.45 ×1022cm-3
u电阻率比普通金属大1~2个数量级：
Bi：//c 127 ×10-6(Ω⋅cm)；⊥c 100 ×10-6(Ω⋅cm)
Sb：//c 29.3×10-6(Ω⋅cm)；⊥c 38.4 ×10-6(Ω⋅cm)
金属Cu：1.55 ×10-6(Ω⋅cm)
禁带
满带
Ch.5 晶体中电子在外场中的运动
56/110山西大学物电学院
利用材料模拟计算软件Materials Studio中的 CASTEP
模块计算的半金属As晶体(rhomb)的能带和分波能态密度
33As：4s24p3
4p
4s
返
回
4s
4p
Γ
价
带
导
带
Ch.5 晶体中电子在外场中的运动
57/110山西大学物电学院
由于能带交叠，能带1中的部分电子转
移到能带2中，而在能带1中形成空穴，
讨论 T = 0K 时的费密能级。
解：半金属的能带1和能带2如图所示。
首先计算能态密度，再求T= 0K时
费密能级。
其中E1(0)为能带1的带顶，E2(k0)为能带2的带底，交叠部分
【例】半金属交叠的能带：
2
2
2 2 0 0 2
2
( ) ( ) ( ) , 0.062E k E k k k m mm= + − =
r rh
1 2 0(0) ( ) 0.1E E k eV− =
2 2
1 1 1
1
( ) (0) , 0.182
kE k E m mm= − =h
Ch.5 晶体中电子在外场中的运动
58/110山西大学物电学院
能态密度的一般表达式为：
3( ) 2
(2 ) k
V dSN E
Eπ
=
∇∫∫Ò
等能面
对能带1：
2 2
1 1
1
( ) (0) ,
2
kE k E
m
= −
h
2
1 1/k E k m∇ = h 1 1 12[ (0) ( )] /E E k m= −h
2
1 1 3
1 1 1
4( ( )) 2
(2 ) 2[ (0) ( )]/
V kN E k
E E k m
π
π
=
−h
3
1 2
1 12 2
22 ( ) (0) ( )
(2 )
mV E E k
π
= −
h
1 1 12 [ (0) ( )]m E E k
k
−
=
h
则能带1的能态密度为：
ky
O kx
k
1 1(0) ( )E E k−
Ch.5 晶体中电子在外场中的运动
59/110山西大学物电学院
对能带2：
2
2
2 2 0 0
2
( ) ( ) ( ) ,
2
E k E k k k
m
= + −
r rh
3
2 2
2 2 02 2
22 ( ) ( ) ( )
(2 )
mV E k E k
π
= −
h
2 2 2 0
0
2 [ ( ) ( )]
| |
m E k E k
k k
−
− =
r r
h
则能带2的能态密度为： 3( ) 2
(2 ) k
V dSN E
Eπ
=
∇∫∫Ò
等能面
2
0
2
2
| |
k
k kE m
−
∇ =
r r
h 2 2 0
2
2[ ( ) ( )]E k E k
m
−
= h
2
0
2 2 3
2 2 0 2
4 | |( ( )) 2
(2 ) 2[ ( ) ( )]/
k kVN E k
E k E k m
π
π
−
=
−
r r
h
ky
O kx
2 2 0( ) ( )E k E k−
0| |k k−
r r
Ch.5 晶体中电子在外场中的运动
60/110山西大学物电学院
半金属如果不发生能带重合，电子刚好填满一个能带。
由于能带交叠，能带1中的电子填充到能带2中，满足
0
1
0
2 0
(0)
1 1 1 2 2 2( )
( ) ( )F
F
E E
E E k
N E dE N E dE=∫ ∫
1
0
3 (0)
2
1 1 1 1( ) (0) ( )
F
E
E
m E E k dE−∫
0
2 0
3
2
2 2 2 0 2( )
( ) ( ) ( )FE
E k
m E k E k dE= −∫
1
0
(0)3 3
2 2
1 1 1[ (0) ( )]
F
E
E
m E E k− −
0 0
1 1 2 2 0[ (0) ] [ ( )]F Fm E E m E E k− = −
0 1 1 2 2 0
1 2
(0) ( )
F
m E m E kE m m
+
=
+
0
2 0
3 3
2 2
2 2 2 0
( )
[ ( ) ( )]
FE
E k
m E k E k= −
1 20.18 , 0.06 ,m m m m= = 1 2 0(0) ( ) 0.1E E k eV− =
0
2 0( ) 0.075FE E k eV= + 1(0) 0.025E eV= −
Ch.5 晶体中电子在外场中的运动
61/110山西大学物电学院
三、近满带和空穴
满带中少数电子受激发而跃迁到空带中去，使原来的满带变
成近满带，近满带中这些空的状态，称为空穴(hole)。
空穴在外场中的行为，犹如它带有正电荷+e的粒子。
1)假设近满带中有一个k态中没有电子，我们可以设I(k)为
这种情况下整个近满带的总电流。
设想在空的 k 态中填入一个电子，这个电子对电流的贡献
为 −ev(k)。但由于填入这个电子后，能带变为满带，因此总电
流为0，即
( ) ( ) 0I k ev k + − = 
r rr r
， ( ) ( )I k ev k=
r rr r
这表明近满带的总电流，就如同一个带正电荷e、速度为
电子在空的 k 态中的速度的一个粒子运动所产生的一样。
或
Ch.5 晶体中电子在外场中的运动
62/110山西大学物电学院
Ch.5 晶体中电子在外场中的运动
63/110山西大学物电学院
2)有电磁场存在时，设想在k态中仍填入一个电子形成满
带。而满带电流始终为0，对任意 t 时刻都成立。
( ) ( )d dI k e v k
dt dt
=
r rr r
作用在k态中电子上的外力为 { }( )F e ε v k B− + ×
rr rr r=
电子的准经典运动：
*
dv F
dt m=
rr
( )d I k
dt
rr { }
2
( )
*
e v k B
m
ε= − + ×
r rr r
( ) ( )I k ev k=
r rr r
，
{ }| * |
) (( )d I k e ev k B
d
e
mt
ε + ×=
r rr rrr
而在能带顶附近，电子的有效质量为负值，m* < 0，
该式表明：在有电磁场存在时，近满带的电流变化就如同一
个带正电荷e，具有正有效质量m*的粒子一样。
Ch.5 晶体中电子在外场中的运动
64/110山西大学物电学院
结论：当满带顶附近有空状态k时，整个能带中的电流以
及电流在外电磁场作用下的变化，完全如同一个带正电荷e，具
有正有效质量 m*和速度 v(k)的粒子的情况一样。
我们将这种假想的粒子称为空穴(hole)。
空穴是一个带有正电荷e，具有正有效质量的准粒子。它
是在整个能带的基础上提出来的，它代表的是近满带中所有电
子的集体行为。
因此空穴不能脱离晶体而单独存在，它只是一种准粒子。
电子导电性：导带底有少量电子所产生的导电性；
空穴导电性：满带中缺少一些电子所产生的导电性。
混合导电性：满带中的少量电子激发到导带中，产生的导
电性是由相同数目的电子和空穴构成的。
电子和空穴统称为载流子。
Ch.5 晶体中电子在外场中的运动
65/110山西大学物电学院
由于半导体材料的能隙较窄，因而在一定温度下，有少
量电子从价带顶跃迁到导带底，从而在价带中产生少量空
穴，而在导带底出现少量电子。
因此在一定温度下，半导体具有一定的导电性，称为本
征导电性。
ρ
TO
半导体电阻率随温
度的变化
电子的跃迁几率～exp(−Eg/kBT)。
一般半导体禁带宽度 Eg< 3eV，
Eg>>kBT，所以电子的跃迁几率很小，
半导体的本征电导率较低。
温度T升高，电子跃迁几率指数上
升，半导体的本征电导率也随之迅速增
大，电阻率随温度升高随之迅速减小。
T=300K,kBT≈0.026eV
T=800K,kBT≈0.069eV
T=1600K,kBT≈0.138eV
Ch.5 晶体中电子在外场中的运动
66/110山西大学物电学院
在金属中，其导带部分填充，导带
中有足够多的载流子(电子或空穴)，温
度升高，载流子的数目基本上不增加。
但温度T升高，原子的热振动加
剧，电子受声子散射的几率增大，电子
的平均自由程减小，因此金属的电导率
随温度的升高而下降，电阻率上升。
如果半导体中存在一定的杂质，其能带的填充情况将有
所改变，可使导带中出现少量电子或价带中出现少量空穴，
从而使半导体有一定的导电性，称为非本征导电性。微量的
杂质，对半导体的导电性影响很大。
绝缘体的带隙宽，在一般情况下，绝缘体的导电性随温
度的变化不大，难以观察。
ρ
TO
半导体
金属
电阻率随温度的变化
Ch.5 晶体中电子在外场中的运动
67/110山西大学物电学院
§5.4 在恒定磁场中电子的运动
v量子理论：求解含磁场的Schrödinger方程。
讨论晶体中电子在恒定磁场中运动的方法：
v准经典近似：优点是简单且物理图象清晰，缺点是有些量
子效应无法从准经典近似中得出。
一、恒定磁场中的准经典运动
准经典运动的基本方程： 1( ) ( )kv k k= ∇ r
r rr
h E
= ( )k v k B− ×
r r rrh d edt
(a)
(b)
1. 在k空间中的运动图象
1) ，即在k空间中，电子在垂直于磁场 的平
面内运动，即沿磁场方向 的分量不随时间而变。
/dk dt B⊥
r r
B
r
k
r
v B×
rr
Ch.5 晶体中电子在外场中的运动
68/110山西大学物电学院
Lorentz力不做功，电子的能量E不
随时间而变，即电子在等能面上运动。
设磁场沿z方向，即 (0,0, )zB = Be B=
r r
dk ev B
dt
= − ×
r rrh
0 0
x y z
x y z
e e e
e v v v
B
= −
r r r
y x x yev Be ev Be= − +
r r
则 ,yx ev Bdk
dt
= −
h
,y x
dk ev B
dt
=
h
0zdk
dt
=
2) =F v B− ×
r rr
，e F v⊥
r r
，
结论：在k空间中，电子的运动轨迹是垂
直于磁场的平面与等能面的交线，即电
子在垂直于磁场的等能线上运动。
在k空间中，晶体中电子作垂直于磁场的循环运动。
zk C⇒ =
xk
yk
,zk B
r
Ch.5 晶体中电子在外场中的运动
69/110山西大学物电学院
xk
yk
zk B
r
k
r
例如，对自由电子：
2 2
( ) ,2
kE k m=
r h
等能面为球面，电子的回旋轨道为圆。
 ( ) kv k m=
rrr h∵  dk e v Bdt∴ = − ×
r rr
h = ke
m B,− ×
r r
(0,0, )B = B
r
k B×
r r
0 0
x y z
x y z
e e e
k k k
B
=
r r r
y x x yk Be k Be= −
r r
则 ,x
y
dk eB k
dt m
= − ,y
x
dk eB k
dt m
= 0zdk
dt
=
zk C=
等能面
自由电子在k空间做垂直于磁场的圆周运动。
2 2 2 2 2( ) ( ),x y x y
eBk k k km+ = +& & 2 2 2( ) ,eBk km⊥ ⊥=& 回旋圆频率：
0
eB
mω =
回旋轨道 k
irk⊥
Ch.5 晶体中电子在外场中的运动
70/110山西大学物电学院
2. 在实空间中的运动图象
在实空间中，自由电子的运动轨迹为一螺旋线。
0 ,yvω= −
 kv m=
r
r h∵ ，
 x xdv dk
dt m dt∴ = h
0 ,y
x
dv
vdt ω=y
eB
m km= − h 0zdv
dt
=
,x
y
dk eB kdt m= − ,y
x
dk eB kdt m= 0zdk
dt =
0 0cosxv v tω=
2 2 2
0 x yv v v= +
0 0sinyv v tω=
zv C=
其中：
在实空间，自由
电子沿磁场方向作匀
速直线运动，在垂直
于磁场的平面内作匀
速圆周运动──螺旋
运动。
x
z
B
r
y
0
eB
m
ω =
2
2
02 0,x
x
d v v
dt
ω+ =
2
2
02 0,y
y
d v
v
dt
ω+ = 0zdv
dt
=
投影
0sinx A tω=
0cosy A tω= −
z Ct=
Ch.5 晶体中电子在外场中的运动
71/110山西大学物电学院
二、自由电子情况的量子理论
没有磁场时，自由电子的哈密顿量为：
2
2
pH
m
=
存在磁场时，电子运动的哈密顿量为： 21 ( )2H p eAm= +
rr
: 磁场的矢势，B A= ∇ ×
rr
若磁场B沿z方向，则可取
2 2 21ˆ ˆ ˆ ˆ ( )2 x y zH p p eBx pm  ∴ = + + + 
A
r
(0, ,0)A Bx=
r
ˆ ˆˆ ˆ[ , ] [ , ] 0,y zH p H p= = 具有共同本征态ψ：ˆˆ ˆ y zp p H∴ 、 与
ˆ y yp kψ ψ= h
ˆ z zp kψ ψ= h
( )( ) ( )y zi k y k zr e xψ ϕ+=
r
代入Schrödinger方程： Ĥ Eψ ψ=
ˆ xp i x
∂= − ∂h
ˆ yp i y
∂= − ∂h
ˆ zp i z
∂= − ∂h因为哈密顿算符中不含 y和 z，则
 ( , 0,0)A By= −
r
或取
Ch.5 晶体中电子在外场中的运动
72/110山西大学物电学院
2 2 21ˆ ˆ ˆ ˆ( )2 x y zH p p eBx pm  = + + + ，
( )( ) ( )y zi k y k zr e xψ ϕ+=r
Ĥ Eψ ψ=
ˆ y yp kψ ψ= h
ˆ z zp kψ ψ= h
2 2 2 21 ˆ ( ) ( ) ( )
2 x y zp k eBx k x E x
m
ϕ ϕ + + + = h h
2 222 2
2
2
1 ( ) ( ) ) ( )2 2 2
z
y
kd eBm x k x E xm m eB mdx
ϕ ϕ
  − + + = −    
hh h （
2 2
2 2
0 02
1 ( ) ( ) ( )2 2
d m x x x xm dx
ω ϕ εϕ − + − =  
h
令 0 ,eB
mω = 0 ,yx keB= − h 2 2
2
zkE mε = −
h
ˆ xp i
x
∂
= −
∂
h
这是中心位置在x=x0，振动圆频率为ω0的线性谐振子，其解为
则
Ch.5 晶体中电子在外场中的运动
73/110山西大学物电学院
( ) ( ) ( )22
0 0 0
1exp ( )
2n n nx x N x x H x xϕ α α − ≈ − − −  
Nn为归一化因子，Hn(α(x−x0))为厄密多项式， 0mω
α =
h
相应的谐振子能量本征值为
0
1( )
2n nε ω= + h n=0, 1, 2, …
2 2
2
z
n
k
E
m
ε= +
h
( )
0( ) ( )y zi k y k z
nr e x xψ ϕ+= −
r
故自由电子在磁场中运动的波函数和能量本征值为：
即自由电子在垂直于磁场平面内的匀速圆周运动，对应于
一种简谐振动，其能量是量子化的，这些量子化的能级称
为朗道能级(Landau level)。
2 2
0
1( )
2 2
zk
n
m
ω= + +
h
h
Ch.5 晶体中电子在外场中的运动
74/110山西大学物电学院
三、晶体中电子的有效质量近似(Effective mass approximation)
晶体中电子在磁场中运动时，其哈密顿量为
21 ( ) ( )2H p eA V rm= + +
rr r
其中V(r)为晶体的周期性势场，严格求解是很困难的。
前面对自由电子的讨论可以推广到晶体中的电子，只需用电子有效质
量m*代替自由电子质量m即可。一般半导体中，在导带底和价带顶附近常
常可以采用有效质量近似，对有些金属材料(如碱金属)有时也可以采用。
21 ( )
2 *
H p eA
m
= +
rr
在有些情况下，可将哈密顿量近似写成
即把周期场的影响概括成有效质量的变化——有效质量近似。
亦即在研究晶体中载流子运动时，将载流子作为自由电子(或自由空穴)来
处理，但将其质量用有效质量来代替，这种近似方法称为有效质量近似。
由于自由电子的薛定谔方程十分简单，采用这种方法可以极大地减少计算
的工作量。但引入了有效质量，又可以包含固体能带结构的重要信息。
Ch.5 晶体中电子在外场中的运动
75/110山西大学物电学院
四、回旋共振(cyclotron resonance) 
在恒定外磁场作用下，晶体中的电子将做螺旋运动。
回旋频率： 0 *
eB
mω =
若在垂直磁场方向加上频率为ω的交变电场，当ω=ω0时，
交变电场的能量将被回旋的电子共振吸收，这个现象称为回旋
共振(cyclotron resonance)。
按量子理论，共振吸收相当于实现了电子在朗道能级之间
的跃迁。通过测量共振吸收频率，可以确定晶体中电子的有效
质量。
电子回旋共振被广泛地用来测定半导体导带底电子或价带
顶空穴的有效质量，研究其能带结构。
Ch.5 晶体中电子在外场中的运动
76/110山西大学物电学院
§5.5 德·哈斯－范·阿耳芬效应
1930年，De Haas和Van Alphen在低温强磁场中发现，铋
单晶的磁化率χ随磁场的倒数1/B作周期振荡，这种现象称为
De Haas-Van Alphen效应。
后来在许多金属材料中都观
察到了类似现象。
Ch.5 晶体中电子在外场中的运动
77/110山西大学物电学院
这种周期振荡现象与金属费米面附近的电子在强磁场中的
行为有关，因而与金属的费米面结构有密切关系，这些现象是
研究金属费米面结构的有力工具。
通过测定De Haas - Van Alphen效应的振荡周期，确定垂
直于磁场方向费密面的截面积，就可以相当准确地勾画出
费米面的形状。
金属的导电率、比热等物理量在低温强磁场中也有类似的
振荡现象。
在绝对零度，系统的磁矩为 EM B
∂= −
∂
而磁化率χ定义为
0
BM χ µ=
磁化率 χ 随磁场 B 变化而振荡的现象，是系统能量 E 随
磁场变化而振荡的结果。
Ch.5 晶体中电子在外场中的运动
78/110山西大学物电学院
一、自由电子气在恒定磁场中的朗道能级
在垂直于磁场的平面(x~y)内，电子的运动是量子化的，
从准连续的能量：
2 2
2
z
n
k
E m ε= +
h 2 2
0
1( )2 2
zk
nm ω= + +
h
h
1)沿磁场方向(z方向)电子保持自由运动，相应的动能：
2 2
2
zk
m
h
量子化的能级：
2
2 2( )2 x yk km +h
0
1( )2n ω+ h
间隔为：hω0
垂直磁场下
简并到
(1/2)hω0n=0E
－
h2
k z
2 /2
m
(3/2)hω0n=1
(5/2)hω0n=2
(7/2)hω0n=3
可见，郎道能级是高度简并的，每一郎道能级包含量子
态的数目等于原来准连续谱中能量间隔hω0内量子态的数目。
B = 0 B ≠ 0
Ch.5 晶体中电子在外场中的运动
79/110山西大学物电学院
3)电子的能量由准连续的能谱
变成一维的子能带。
每个子能带都是一条抛物线，
量子数n就是子能带的序号。
n=0是最低的子能带，n增加，
子能带向上移，各能带有一定交
叠，如图给出子能带的简图。
2)在与磁场垂直的(kz=常数)平面内，等能面
为一系列同心圆；沿磁场方向的kz取值是准连续
的，从而形成一系列“圆柱面(郎道面)”。
每一个“圆柱面”对应一个确定的量子数n，
可以看成是一个子能带(次能带)，在每一个子能
带中只有一维自由度kz。
E
zkO
0B =
0n =
1n =
2n =
3n =
B
r2 2
2
z
n
kE m ε= +
h 2 2
0
1( )2 2
zk nm ω= + +
h h
0
1
2
ωh
0
3
2
ωh
0
5
2
ωh
0
7
2
ωh
FE
Ch.5 晶体中电子在外场中的运动
80/110山西大学物电学院
二、自由电子气朗道能级的简并度
2 2
2 2
0 02
1 ( ) ( ) ( )2 2
d m x x x xm dx
ω ϕ εϕ − + − =  
h
在垂直于磁场的平面内，自由电子作简谐振动，波动方程为
其中 0 ,eB
m
ω = 0 ,yx k
eB
= −
h 2 2
2
zk
E
m
ε = −
h
这是中心位置在x=x0，振动圆频率为ω0的线性谐振子。
不同的x0并不影响谐振子的本征值ε，但x0依赖于波矢分量
ky，因此不同的ky代表的状态可能会是简并态。
若三维晶体边长分别为Lx , Ly, Lz，则 x0 取值应满足：
0 ,2 2
x xL Lx− ≤ ≤ 即 ,2 2
x x
y
L LkeB− ≤ − ≤h
,2 2
x x
y
eBL eBLk− ≤ ≤h h
Ch.5 晶体中电子在外场中的运动
81/110山西大学物电学院
,
2 2
x x
y
eBL eBLk− ≤ ≤
h h
由边界条件，ky取值是均匀间隔的点，
间隔为2π /Ly，则在上述取值范围内ky
的取值数(即x0的取值数)为：
2x
y
eBL
L
π
α =
h
如果计入自旋乘以2，则得郎道能级的简并度： x yeL L
D Bπ= h
简并度D与磁感应强度B成正比，与能量无关，即无论能量
为何值(量子数n为何值)，简并度不变。
若B=1T，Lx= Ly =1cm，则D≈1011，高度简并。
无磁场时，状态代表点均匀分布(kx~ky平面)，密度为 2 ;
(2 )
x yL L
π
有磁场时，状态代表点分布改变，同一n、不同kx、ky具有
同一能量。在kx~ky平面，对应半径为
kx
ky
无外磁场状态代表点2
x yeL L B
π
=
h
Ch.5 晶体中电子在外场中的运动
82/110山西大学物电学院
2 2
02
2 1( )2x y
mk k n ω+ = + h
h
的圆周，同一n的状态代表点在同一圆周上。
ky
kx0
n n+1
相邻二圆环之间的面积：
0 02 2
2 3 2 1( ) ( )2 2
m mn nπ ω π ω+ − +h h
h h 02
2mπ ω= h
h
0 ,eB
mω =
2 eBπ= h
则此面积内含有原来没有磁场时的状态代表点数是
2(2 )
x yL L
π
2 eBπ
⋅
h 2
x yeL L B
π
=
h
α=
说明无磁场时kx~ky平面上均匀分布的状
态代表点，在磁场中都聚合到圆周上，每
个圆周上的状态代表点数为α。
圆周代表能量为
0
1( ) ,2n nε ω= + h
的简并态，每个能态的简并度为D。
n=0, 1, 2, …
kx
ky
有外磁场状态代表点
0n=
1n=
2n=
Ch.5 晶体中电子在外场中的运动
83/110山西大学物电学院
dkz
kz三、由能态密度解释De Haas-Van Alphen效应
1. 第n个子能带的能态密度N(E,n)
外加磁场后，状态代表点都汇聚到郎道面上。
圆周上波矢代表点数为α，在dkz区间kz有(Lz/2π) dkz个值，
计及自旋，在第n个子能带波矢 kz ~ kz+dkz范围的量子态数：
2
2
z
z
L
dkα
π 2
z
z
L
D dk
π
=
2 2
0
1( )
2 2
zk
E n
m
ω= + +
h
h ，
1/ 2 1/ 2
02
2 1) [ ( ) ]
2z
mk E n ω= − + h
h
（
1/ 2 1/ 2
02
1 2 1) [ ( ) ]
2 2z
mdk E n dEω −= − + h
h
（
2x yeL L
D B απ= =h
又
2
x yeL L
Bα π= h
Ch.5 晶体中电子在外场中的运动
84/110山西大学物电学院
1/ 2
0
2 1[ ( ) ]
2 2
zL m
D E n dEω
π
−= − + h
h
将dkz换算成dE，并考虑到E(−kz)=E(kz)，则在第n个子能带(第n
个郎道面)，能量在 E ~ E+dE之间的量子态数：
2
2
zL
dZ D
π
= ⋅ 1/ 2 1/ 2
02
1 2 1) [ ( ) ]
2 2
m E n dEω −⋅ − + h
h
（
故得第n个子能带的能态密度：
1/ 2
0
2 1( , ) [ ( ) ]
2 2
zL m
N E n D E n ω
π
−= − + h
h
2. 总能态密度N(E)
能量等于E 的电子可以处于不同的子
能带，所以总的能态密度应是能带底位于
E以下所有子能带对应能态的累计：
E
zkO
0B =
0n =
1n =
2n =
3n =
E
1 2
3 20
02 2
2 1( , ) ( ) ( )2(2π)
V mN E n E nω ω
−
 = − +  
h h
h或
x yeL L
D Bπ= h
x y zV L L L=
0
eB
mω =
Ch.5 晶体中电子在外场中的运动
85/110山西大学物电学院
1 2
3 20
02 2
0
2 1( ) ( ) ( )2(2π)
n
n
V mN E E nω ω
−′
=
 = − +  ∑h h
h
其中 的子能带的能带底刚好等于
E或稍低(如图中取n’=3)。
在没有磁场时的能态密度为
n n′=
由能态密度表达式，可以定性
画出有磁场和无磁场时，能态密度
随 E 变化曲线。其中：
虚线表示第n个子能带的能态
密度曲线。
实线表示总能态密度曲线。
E
zkO
0B =
0n =
1n =
2n =
3n =
E
( )3 / 2
0 2 2
2( )
2
V mN E E
π
=
h
0B =
1 2 3 4Ｅ/hω0
0
N(E)
0B ≠
0n = 1n = 2n = 3n =
Ch.5 晶体中电子在外场中的运动
86/110山西大学物电学院
3. 磁化率振荡的原因
晶体总电子数N一定，磁场加入前后，费米能量EF不变。
1)E＝(n+1/2)hω0处能态密度出现峰值
(状态密度峰，Landau峰)；
2)相邻峰值间能量差为hω0=heB/m；
3)随着B增大，能态密度也增大，每
个峰内包含的量子态数增多，可以容纳
更多的电子。
主要特点
0B =
1 2 3 4Ｅ/hω0
0
N(E)
0B ≠
0n = 1n = 2n = 3n =
随着B增加，子能带能量和量子态数相应增加，间隔hω0
也增加，而N不变，所以电子将在各个子能带中再重新分布。
Ch.5 晶体中电子在外场中的运动
87/110山西大学物电学院
随着磁场B的增强，电子从上一子能带转到比它能量低的其
它子能带时，如上图，系统总能量从(a)→(c)增大，从(c)→(e)减
小，从(e)→(f)又增大，(a)→(e)完成一个周期。
B
EF
n +1
n
n +1
n
n +1
n
n +1
n
n −1
n
n −1
n
(a) (b) (c) (d) (e) (f)
x yeL L
D Bπ= h
0
eB
mω =h h
hω0
B 
= 
0
B=B1
B 
= 
0
B=B2
B 
= 
0
B=B3
B 
= 
0
B=B4
B 
= 
0
B=B5
B 
= 
0
B=B6
系统总能量随B的周期性变化
T=0K
Ch.5 晶体中电子在外场中的运动
88/110山西大学物电学院
郎道能级电子填充情况随磁
感应强度B的变化
B
B=B1 B=B2
B=B1时，第n个峰被占据，
11( )2F
eBE n m= + h ，
1
( 1/ 2)1
F
n e
B mE
+= h
B=B2时，第n-1个峰被占据，
21( )2F
eBE n m= − h ，
2
( 1/ 2)1
F
n e
B mE
−= h
1 2
1 1 1( )B B B∆ = −
F
e
mE= h
变化周期大致估计如下：
n +1
n EF n-1
n
0
eB
mω =
B 
= 
0
B 
= 
0
hω0
当B增大时，电子可能填充的Landau峰数下降，但EF不变。
Ch.5 晶体中电子在外场中的运动
89/110山西大学物电学院
①磁场B增强时，每满足这一条件，电子占据的峰就
少一个。即电子从上一子能带转到比它能量低的其它子能
带，系统总能量将以 ∆(1/B)为周期随1/B变化振荡；
1( )
F
e
B mE∆ = h
2
3
2
0 2(3 )
2F F en
m
E E π≈ = h
2
321 2( ) (3 )e
e nB π −∆ = h
ne──系统电子数密度
在低温时，
即
对球形等能面， 2 2 / 2 ,F Fk mE = h
ky
kz
0
kx
B
r
kF
SF
2
21( )
F
e
B k
∆ =
h
2
FS
eπ= h
SF──垂直磁场方向费密面的极值截面积。
Ch.5 晶体中电子在外场中的运动
90/110山西大学物电学院
B
r
②随着B增强，hω0 增加，如图所示费米面内的最大圆柱
面，首先扩大而越过费密面，这时电子被抽空而填入费密面内
的其余圆柱面上。
相应的能态密度在费米能之下的Landau峰就减少一个。
所以当一个圆柱面越过费密面时，电子的总能量便出现一
次突变，电子进行一次再分布。
FE
E
zkO
0B ≠
0n =
2n =
3n =
EF
1n =
4n =
0B =
1 2 3 4Ｅ/hω0
0
N(E)
0B ≠
0n = 1n = 2n = 3n =
kz
EF
Ch.5 晶体中电子在外场中的运动
91/110山西大学物电学院
③系统的磁矩 磁化率 亦随1/B呈
周期变化，此即De Haas-Van Alphen效应。
④对于晶体中的Bloch电子，总能量、磁化率等物理量亦随
1/B出现类似的振荡现象，其振荡周期亦与垂直于磁场方向的费
米面极值截面积SF成反比。
原则上，改变磁场方向，测出振荡周期，可得到垂直于该
方向的SF，然后根据不同方向的SF决定费密面的形状。
/ ,M E B= −∂ ∂ 0 / ,M Bχ µ=
Ch.5 晶体中电子在外场中的运动
92/110山西大学物电学院
四、应用举例
1)碱金属，例如K、Na，具有bcc结构，每个原胞内有2个
电子。晶格常数为a的体心立方的倒格子是“晶格常数”为
a*=4π/a的面心立方，简约BZ是一个菱形12面体。
若把导带电子看成是完全自由的，则
Fermi面半径： 2 1/ 3(3 )F ek nπ= 32/en a=
2
1/ 3
3
6( )Fk
a
π= 1/ 33 2( ) ( )4 a
π
π= 20.620( )a
π=
简约BZ内，内切球半径(ΓN)：
Γ
H
N
1 42( )4mk a
π= 2 2 2( ) 0.707( ),2 a a
π π= =
可见，Fermi面在FBZ内，且不靠近BZ界面，所以Fermi
面可视为球面，在不同方向上有相同的极值面积。
在不同方向上振荡周期相同，与实验结果一致。
故碱金属中价电子行为接近自由电子。
kF
0.877F
m
k
k =
Ch.5 晶体中电子在外场中的运动
93/110山西大学物电学院
2)贵金属，例如Cu、Ag、Au，具有fcc结构，其倒格子体
心立方，简约BZ是一个截角8面体。其外壳层只有1个s电子，
每个原胞内有4个电子。若把其中的电子看成是自由的，则
2 1 / 3(3 )F ek nπ=
1/ 33 2( ) ( )2 a
π
π= 20.782( )a
π=2 1/ 3
3
4(3 )
a
π=
1 43( )4mk a
π= 3 2 2( ) 0.866( )2 a a
π π= =
Fermi面虽在FBZ内，但它在<111>方向
上与8个正六角面很接近，在这些方向上球
形Fermi面发生畸变，有8个颈状突起部分与
fcc的FBZ的8个六角面相接触。
显然，在不同方向上Fermi面与磁场垂直
的极值轨道面积不同，振荡周期也相同。
B
r
34/en a=
/ 0.903F mk k =
Ch.5 晶体中电子在外场中的运动
94/110山西大学物电学院
21( )
FB S
eπ∆ = h
B
r
右图为磁场沿 <111> 方
向时 Ag 的 De Haas - Van 
Alphen 振荡，振荡包含两个
周期。
在Fermi面上与磁场垂直
的极值轨道有两个：
“肚子”轨道：截面积SF
大，∆(1/B)的周期小(实线)；
“脖子”轨道：截面积SF
小，∆(1/B)的周期大(虚线)。
肚子
脖子
肚子
脖子
Ch.5 晶体中电子在外场中的运动
95/110山西大学物电学院
右上图为磁场沿不同方向时金属Ag
费米面的三个极值轨道(a:电子轨道，b:空穴
轨道，c:开放轨道)，四个延展区的费米面
中间围成的区域，俗称“狗骨头”轨道。
改变磁场方向，测定 De Haas-Van 
Alphen效应的振荡周期，确定极值截面的面
积，就可相当准确地勾画出费密面的形状。
Dog’s
 bone
若在垂直磁场的k平面中电子运动轨道
为开放轨道(如右下图示)，电子运动不形成闭
合轨道(B→A→B)，此时没有De Haas-Van 
Alphen效应。但有明显的磁阻效应(——磁场
而引起的半导体或导体电阻的变化)，分析磁阻效应
可得到有关费密面的信息。
Ch.5 晶体中电子在外场中的运动
96/110山西大学物电学院
1B
r
2B
r
zk
r
xk
r
yk
r
多极值轨道：
对如图所示费密面，
如果磁场取为kz方向，
那么与kz垂直的极值截面积
有(1)极大、(2)极大和(3)极
小；
如果磁场取为ky方向，
那么只有一个极大截面积
(4)存在。
Ch.5 晶体中电子在外场中的运动
97/110山西大学物电学院
第五章 小 结
一、准经典运动
1. 波包的概念
2. 准经典运动的基本方程
3. 电子的加速度
1( ) ( )kv k E= ∇ r
rr
h
p k=
rr h( )d kF
dt
=
r
r h
2
1 ( )k ka FE = ∇ ∇ 
 
r r
rr
h
4. 有效质量概念
1
2
1* ( )k km E
−
 = ∇ ∇ 
 
r r
h
Ch.5 晶体中电子在外场中的运动
98/110山西大学物电学院
由于有效质量是二阶张量，在一般情况下，电子的加
速度与所受的外场力的方向并不一致。
2 2 2
2
2 2 2
2 2
2 2 2
2
1 1
x x y x z
y x y y z
z x z y z
E E E
k k k k k
E E E
m k k k k k
E E E
k k k k k
∗
 ∂ ∂ ∂
 
∂ ∂ ∂ ∂ ∂ 
 ∂ ∂ ∂   =   ∂ ∂ ∂ ∂ ∂ 
 
∂ ∂ ∂ 
 ∂ ∂ ∂ ∂ ∂ 
h
倒有效质量张量：
2
2
1 1 E
m k kαβ α β
∗
∂
=
∂ ∂h
倒有效质量张量的分量为：
Ch.5 晶体中电子在外场中的运动
99/110山西大学物电学院
二、导体、绝缘体和半导体
v导带、满带和近满带的导电能力；
v导体、绝缘体和半导体能带结构及其对导电性的影响；
v半导体的本征导电性与非本征导电性；
v金属导体和半导体的本征导电率(或电阻率)随温度的变化规
律有何不同？其导电机制有何不同？
金属：导电率随温度的升高而下降，金属电阻的产生；
本征半导体：导电率随温度的升高而迅速上升。
v二价碱土金属之所以是金属导体的原因是由于其最外层的
ns能带与其上面的能带发生能带重叠。
Ch.5 晶体中电子在外场中的运动
100/110山西大学物电学院
当原子组成晶体时，能级过渡成能带。
导体
导
带
半导体绝缘体
禁
带
空带
禁带宽能带无重叠
E
能带重叠
不满带
禁带
禁带窄
空带
T=0K
不满带
T≠0K
禁带
1.导体：碱金属，如Na： 1622 3s2p2s1s ，3s电子只占一半能带。
碱土金属，如Mg： 2622 3s2p2s1s ，能带重叠，出现不满带。
2.绝缘体：禁带宽度一般都较宽， Eg >5eV。
如α-Al2O3： Eg~ 8 eV；NaCl： Eg~ 6 eV。
3.半导体：禁带宽度一般较窄：Eg介于0.2 ~ 3.5 eV之间 .
常规半导体：
Si: Eg ~1.1eV
Ge: Eg~0.7eV
GaAs:Eg~1.5eV
宽带隙半导体：
β-SiC: Eg~2.3eV
ZnO: Eg~3.4eV
TiO2: Eg~3.0eV
热激发
价带 价带满带 满带
二
价
金
属
Ch.5 晶体中电子在外场中的运动
101/110山西大学物电学院
v空穴是一种带正电荷e ，具有正的有效质量|m*|的准
粒子；
v空穴反映的是近满带中所有电子的集体行为，它不
能脱离晶体而单独存在，只是一种准粒子；
v电子导电性：导带底有一些电子所产生的导电性；
空穴导电性：价带顶缺少一些电子所产生的导电性；
v金属中的载流子既可以是电子也可以是空穴。
三、空穴的概念
Ch.5 晶体中电子在外场中的运动
102/110山西大学物电学院
四、电子在恒定电场和磁场中的运动
1. 电子在恒定电场中的运动图象
v在k空间中的运动图象： 电子在k空间中作循环运动；
电子速度作周期振荡。
v在实空间中的运动图象：电子在
实空间中作往返振荡。
v电子的振荡过程很难被观察到。
原因：电子在相邻两次碰撞间的平均自由时间τ太短；
加在样品上的外电场不可能太强。
/ aπ− / aπ
.dk const
dt
=
( )E k
k →
eε →
AA’ v
0
k
x
A  B  C 带隙
下能带 上能带
Ch.5 晶体中电子在外场中的运动
103/110山西大学物电学院
xk
yk
,zk B
r
2. 在恒定磁场中的运动图象
v在k空间中的运动图象：电子的运动轨
迹是一条垂直于磁场的等能线；
v在实空间中的运动图象：自由电子的
运动轨迹是一条沿磁场方向的螺旋线。
1( ) ( )kv k k= ∇ r
r rr
h
E
= ( )k v k B− ×
r r rrh d e
dt
xk
yk
zk B
r
k
r
=Czk
等能面
k⊥
回旋轨道 k
r&
对自由电子： 0
eB
m
ω =
0 0cosxv v tω= 2 2 2
0 x yv v v= +
0 0sinyv v tω=
zv C= 0
eB
m
ω =
x
z
B
r
y
1)恒定磁场中的准经典运动
Ch.5 晶体中电子在外场中的运动
104/110山西大学物电学院
2) 自由电子的量子理论
图象：自由电子在实空间中垂直于磁场平面内的匀速圆周
运动对应于一简谐振子，其量子化能级称为朗道能级。
3. 晶体中电子的有效质量近似
对自由电子的讨论可以推广到晶体中的电子，只需用电子
的有效质量m*代替自由电子的质量m即可。
──即把周期场的影响概括成有效质量的变化。
2 2
2
z
n
k
E
m
ε= +
h
( )
0( ) ( )y zi k y k z
nr e x xψ ϕ+= −
r
电子运动的波函数和能量本征值为：
2 2
0
1( )
2 2
zk
n
m
ω= + +
h
h
Ch.5 晶体中电子在外场中的运动
105/110山西大学物电学院
五、电子回旋共振和De Haas－Van Alphen效应
1. 电子回旋共振
应用：测量半导体导带底附近的电子和价带顶附近的
空穴的有效质量，研究其能带结构。
在恒定外磁场作用下，晶体中的电子将做螺旋运动。
若在垂直磁场方向加上频率为ω的交变电场，当ω=ω0(回旋
频率)时，交变电场的能量将被电子共振吸收，这个现象称为回
旋共振。
通过测量共振吸收频率，可以确定晶体中电子的有效质量。
Ch.5 晶体中电子在外场中的运动
106/110山西大学物电学院
2. De Haas－Van Alphen效应
基本原理：与金属费米面附近电子在低温强磁场的行为有关。
应用：研究金属的费米面结构。
低温下强磁场中金属的磁化率随磁场倒数周期性振荡的现象称
为德哈斯-范阿尔芬效应。
在某一方向如z方向加上磁场后，电子能量变为：
2 2
2
z
n
k
E
m
ε= +
h 2 2
0
1( )
2 2
zk
n
m
ω= + +
h
h
1)沿磁场B方向，电子保持自由运动，相应的动能为 ,
2 2
2
zk
m
h
在垂直磁场的平面内做匀速圆周运动，回旋频率为
m
eB
=0ω
Ch.5 晶体中电子在外场中的运动
107/110山西大学物电学院
2)在垂直磁场的x-y平面上，电子的运动是量子化的，从准连
续的能量 变成(n+1/2)hω0。
2
2 2( )2 x yk km +h
在与磁场垂直的 kz＝C 的平面内，轨道是量子化的。这些
量子化的能级称为朗道能级。
(1/2)hω0n=0
E−
h2 k
z2 /2
m
(3/2)hω0n=1
(5/2)hω0n=2
(7/2)hω0n=3
E
zkO
0B =
0n =
1n =
2n =
3n =
0
1
2
ωh
0
3
2
ωh
0
5
2
ωh
0
7
2
ωh
B
r子能带
3)在与磁场垂直的(kz=常数)平面内，等能面
为一系列同心圆(郎道环)；沿磁场方向的kz取值是
准连续的，从而形成一系列“圆柱面(郎道面)”。
Ch.5 晶体中电子在外场中的运动
108/110山西大学物电学院
4)朗道能级简并度：
π π
c
x y x y
m eBD L L L L
ω
= =
h h
此简并度与磁感应强度B成正比，与能量无关，即无论能量
为何值，简并度不变。
波矢空间状态代表点
kx
ky
无外磁场状态代表点
kx
ky
有外磁场状态代表点
0n=
1n=
2n=
Ch.5 晶体中电子在外场中的运动
109/110山西大学物电学院
5)能态密度
1 2
3 20
02 2
0
2 1( ) ( ) ( )
(2π) 2
n
n
V mg E E n
ω
ω
−′
=
 = − +  
∑h
h
h
0B =
1 2 3 4Ｅ/hω0
0
g(E)
0B ≠
0n = 1n = 2n = 3n =
1)E＝(n+1/2)hω0处能态密度出现峰值
(Landau峰)；
2)相邻峰值间能量差为hω0=heB/m；
3)随着B增大，能态密度也增大，每
个峰内包含的状态数增多，可以容纳更
多的电子。
主要特点
4)低温强磁场中金属的磁化率随磁场倒数周期性振荡的周期：
1 2
F
e
B S
π ∆ = 
  h
SF为垂直磁场方向费密面的极值截面积。
Ch.5 晶体中电子在外场中的运动
110/110山西大学物电学院
少
壮
不
努
力
，
老
大
徒
伤
悲
。
诸
葛
亮