概要信息：

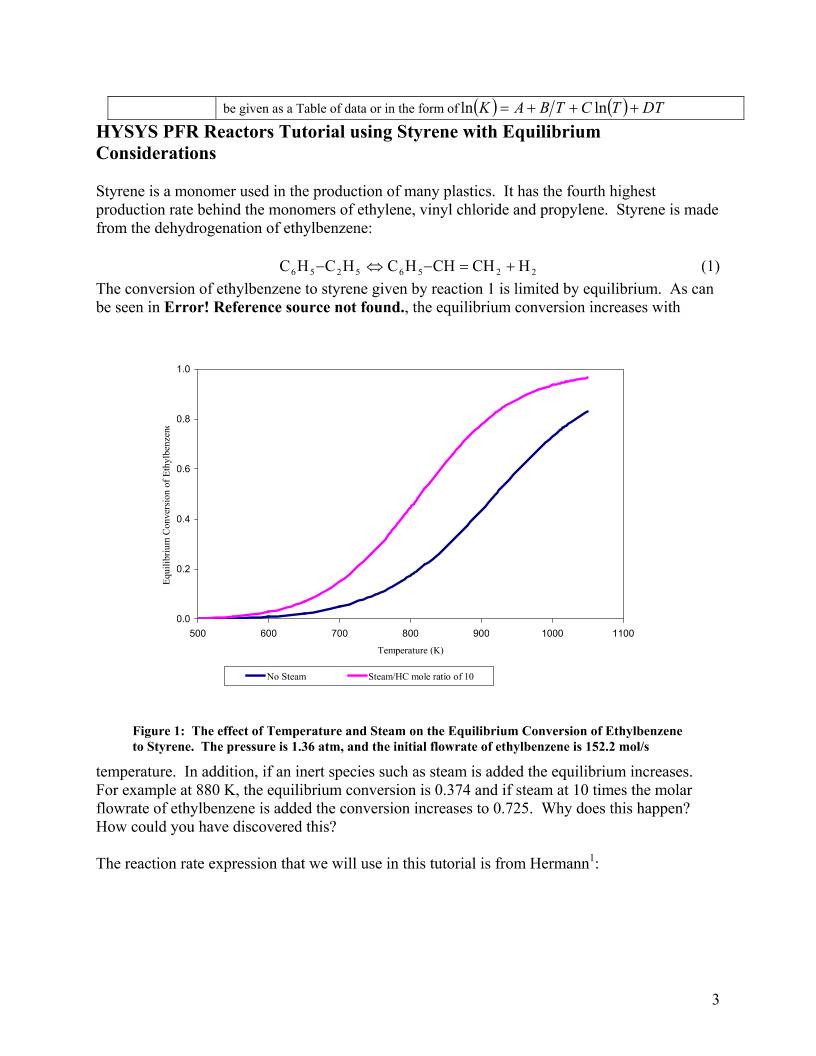
Equilibrium Constant in a Reaction rate in a PFR Reactors:  HYSYS 
By Robert P. Hesketh  Spring 2003 
 
In this session you will learn how to use equilibrium constants within a reaction rate expression 
in HYSYS.  You will use the following HYSYS reactors 
• simple reaction rate expression in a PFR 
• equilibrium reaction rate in an Equilibrium Reactor 
• Gibbs reactor.   
In addition to learning how to use these reactors you will be introduced to the following HYSYS 
tools: 
• Adjust Unit Operation 
• Use of Databook to make 3-D figures 
• Define a new stream from an existing stream 
• Investigate the Temperature Independent Properties 
• Clone a Chemical Species to alter temperature dependent chemical properties 
 
Table of Contents 
Reactor Types in HYSYS ............................................................................................................... 1 
1) CSTR model reactors – Well Mixed Tank-Type.................................................................... 1 
2) Plug Flow Reactor:  Simple Rate, Heterogeneous Catalytic, Kinetic .................................... 2 
Reaction Sets (portions from Simulation Basis:  Chapter 5 Reactions) ......................................... 2 
Summary of Reactions in HYSYS.............................................................................................. 2 
HYSYS PFR Reactors Tutorial using Styrene with Equilibrium Considerations .......................... 3 
Equilibrium - Theory .................................................................................................................. 4 
Hand Calculations for Keq.......................................................................................................... 6 
Using the Adjust Unit Operation .............................................................................................. 15 
Examine Equilibrium Results at Large Reactor Volumes ........................................................ 16 
Equilibrium Reactor...................................................................................................................... 20 
Minimization of Gibbs Free Energy ......................................................................................... 24 
Gibbs Reactor................................................................................................................................ 25 
Submission:................................................................................................................................... 26 
 
The references for this section are taken from the 2 HYSYS manuals: 
Simulation Basis:  Chapter 5 Reactions 
Operations Guide:  Chapter 9 Reactors 
 
Reactor Types in HYSYS 
1) CSTR model reactors – Well Mixed Tank-Type 
HYSYS Reactor Name Reaction Types (See above) 
Conversion Reactor Conversion ( ) 2
210% TCTCCX ++=
CSTR Simple Rate, Heterogeneous Catalytic, Kinetic 
Equilibrium Reactor ( )TfKeq = ; equilibrium based on reaction stoichiometry.   predicted 
from Gibbs Free Energy 
eqK
eqK  specified as a constant or from a table of values 
Gibbs minimization of Gibbs free energy of all specified components, 
 1
option 1) no the reaction stoichiometry is required 
option 2) reaction stoichiometry is given 
 
2) Plug Flow Reactor:  Simple Rate, Heterogeneous Catalytic, Kinetic 
 
Taken from:  9.3 Plug Flow Reactor (PFR)  
 
The PFR (Plug Flow Reactor, or Tubular Reactor) generally consists of a bank of cylindrical 
pipes or tubes. The flow field is modeled as plug flow, implying that the stream is radially 
isotropic (without mass or energy gradients). This also implies that axial mixing is negligible.  
 
As the reactants flow the length of the reactor, they are continually consumed, hence, there will 
be an axial variation in concentration. Since reaction rate is a function of concentration, the 
reaction rate will also vary axially (except for zero-order reactions). 
 
To obtain the solution for the PFR (axial profiles of compositions, temperature, etc.), the reactor 
is divided into several subvolumes. Within each subvolume, the reaction rate is considered to be 
spatially uniform. 
 
You may add a Reaction Set to the PFR on the Reactions tab. Note that only Kinetic, 
Heterogeneous Catalytic and Simple Rate reactions are allowed in the PFR. 
 
Reaction Sets (portions from Simulation Basis:  Chapter 5 Reactions) 
Reactions within HYSYS are defined inside the Reaction Manager. The Reaction Manager, 
which is located on the Reactions tab of the Simulation Basis Manager, provides a location from 
which you can define an unlimited number of Reactions and attach combinations of these 
Reactions in Reaction Sets. The Reaction Sets are then attached to Unit Operations in the 
Flowsheet. 
 
Summary of Reactions in HYSYS 
Reaction Type Description: 
Conversion Conversion% ( ) 2
210% TCTCCX ++=
Equilibrium ( )TfKeq = ; equilibrium based on reaction stoichiometry.   predicted or specified eqK
Gibbs minimization of Gibbs free energy of all components 
Kinetic γϕβα
SRrevBAfA CCkCCkr +−=  where the reverse rate parameters must be thermodynamically 
consistent and rate constants are given for both the forward and reverse rate constant by 
( )RTEATk n −= exp  
Heterogeneous 
Catalytic 
Yang and Hougen form: 
∑+






−
=−
i
ii
s
S
r
Rb
B
a
A
A CK
K
CCCCk
r γ1
 
This form includes Langmuir-Hinshelwood, Eley-Rideal and Mars-van Krevelen etc. 
Simple Rate 








−−=
eq
SR
BAfA K
CCCCkr
γϕ
βα  in which  is predicted from equilibrium data.   must eqK eqK
 2
be given as a Table of data or in the form of ( ) ( ) DTTCTBAK +++= lnln   
22 HCH +=
HYSYS PFR Reactors Tutorial using Styrene with Equilibrium 
Considerations 
 
Styrene is a monomer used in the production of many plastics.  It has the fourth highest 
production rate behind the monomers of ethylene, vinyl chloride and propylene.  Styrene is made 
from the dehydrogenation of ethylbenzene: 
 
 565256 CHHCHCHC −⇔−  (1) 
The conversion of ethylbenzene to styrene given by reaction 1 is limited by equilibrium.  As can 
be seen in Error! Reference source not found., the equilibrium conversion increases with 
temperature.  In addition, if an inert species such as steam is added the equilibrium increases.  
For example at 880 K, the equilibrium conversion is 0.374 and if steam at 10 times the molar 
flowrate of ethylbenzene is added the conversion increases to 0.725.  Why does this happen?  
How could you have discovered this? 
0.0
0.2
0.4
0.6
0.8
1.0
500 600 700 800 900 1000 1100
Temperature (K)
Eq
ui
lib
riu
m
 C
on
ve
rs
io
n 
of
 E
th
yl
be
nz
en
e
No Steam Steam/HC mole ratio of 10
 
Figure 1:  The effect of Temperature and Steam on the Equilibrium Conversion of Ethylbenzene 
to Styrene.  The pressure is 1.36 atm, and the initial flowrate of ethylbenzene is 152.2 mol/s 
 
The reaction rate expression that we will use in this tutorial is from Hermann1: 
 3
 





−


















−×−= −
P
HStyrene
EBEB K
pp
p
T
r 2
K mol
cal1.987
molcal21874exp
kPa sg
EB mol10491.7
cat
2  (2) 
Notice that the reaction rate has units and that the concentration term is partial pressure with 
units of kPa. 
 
HYSYS Reaction rates are given in units of volume of gas phase.  For example, to convert from units of kgcat 
given in equation 3 to the units required by HYSYS given in equation 4, you must use equation 5.  4 
 
 [ ]
gcats
mol
k
r =  (3) 
 [ ] 3
gasms
mol
=HYSYSr  (4) 
 
( )
φ
φρ −
=
1
cHYSYS rr  (5) 
From the source of the original reaction rate studies1 the properties of the catalyst and reactor are 
given as: 
 445.0=φ  (6) 
 3
catcat mkg2146=catρ  (7) 
 mm7.4=pD  (8) 
For our rates we have been using the units mol/(L s).  Take out a piece of paper and write down 
the conversion from gcat to HYSYS units.  Verify with your neighbor that you have the correct 
reaction rate expression.  Please note that if you change the void fraction in your simulation 
you will need to also change the reaction rate that is based on your void fraction. 
 
 
Equilibrium - Theory 
In HYSYS, for most reactions you will need to input the equilibrium constant as a function of 
temperature.  The equilibrium constant is defined by equation as 
 




 ∆−
=
RT
GK rxnexp  (9) 
for the stoichiometry given by equation 1 the equilibrium constant is defined in terms of 
activities as  
 
EB
Hstyrene
a
aa
K 2=  (10) 
for a gas the activity of a species is defined in terms of its fugacity 
 ii
i
i
i
i pf
f
fa γ===
atm 10  (11) 
where iγ  has units of atm-1. 
Now combining equations 9, 10, and 11 results in the following for our stoichiometry given in 
equation 1, 
 4
 atmexp 




 ∆−
=
RT
GK rxn
P  (12) 
It is very important to note that the calculated value of Kp will have units and that the units 
are 1 atm, based on the standard states for gases. 
 
To predict  as a function of temperature we will use the fully integrated van’t Hoff 
equation given in by Fogler2 in Appendix C as 
rxnG∆
 




∆
+





−
∆−∆
=
R
p
R
pRT
o
R
TP
TP
T
T
R
C
TTR
CTH
K
K
R
R
ln
ˆ11
ˆ
ln  (13) 
Now we can predict 
TPK  as a function of temperature knowing only the heat of reaction at 
standard conditions (usually 25°C and 1 atm and not STP!) and the heat capacity as a function of 
temperature.  What is assumed in this equation is that all species are in one phase, either all gas 
or all vapor.  For this Styrene reactor all of the species will be assumed to be in the gas phase and 
the following modification of equation 13 will be used  
 




∆
+





−
∆−∆
=
R
vapor
p
R
vapor
pRT
vaporo
R
TP
TP
T
T
R
C
TTR
CTH
K
K R
R
ln
ˆ11ˆ
ln  (14) 
The heat capacity term is defined as 
 ( )R
T
T
vapor
pvapor
p TT
TC
C R
−
=
∫ d
ˆ   (15) 
and for the above stoichiometry 
  (16) vapor
p
vapor
p
vapor
p
vapor
p EBHstyrene
CCCC ˆˆˆˆ
2
−+=∆
Now for some hand calculations! 
 
To determine the equilibrium conversion for this reaction we substitute equation 11 into 
equation 10 yielding 
 
EB
Hstyrene
P p
pp
K 2=  (17) 
Defining the conversion based on ethylbenzene (EB) and defining the partial pressure in terms of 
a molar flowrate gives: 
 
( )
P
F
FF
P
F
Fp
T
EBEBi
T
i
i
χ
00
−
==  (18) 
Substituting equation 18 for each species into equation 17 with the feed stream consisting of no 
products and then simplifying gives 
 







−
=
EB
EBEB
T
P
F
F
PK
χ
χ
1
2
0  (19) 
where the total molar flow is the summation of all of the species flowrates and is given by 
 steamHstyreneEBT FFFFF +++=
2
 (20) 
With the use of a stoichiometry table the total flowrate can be defined in terms of conversion as  
 5
 EBEBsteamEBT FFFF χ
000
++=  (21) 
Substituting equation 21 into equation 19 gives the following equation 
 ( ) 







−+
=
EB
EBEB
EBEBT
P
F
FF
PK
χ
χ
χ 1
2
0
0
0
 (22) 
The above equation can be solved using the quadratic equation formula and is 
 
( ) ( )
( )PEB
TPPEBsteamPsteamP
EB KPF
FKKPFFKFK
+
+++−
=
0
000
2
4 0
2
χ  (23) 
There are 2 very important aspects to Styrene reactor operation that can be deduced from 
equation 19 or 22.  Knowing that at a given temperature Kp is a constant then 
1. Increasing the total pressure,P, will decrease χEB 
2. Increasing the total molar flowrate by adding an inert such as steam will increase χEB 
 
The following page gives sample calculations for all of the above.  From these sample 
calculations at a temperature of 880 K the equilibrium constant is 0.221 atm.  At an inlet flowrate 
of 152.2 mol ethylbenzene/s and no steam the conversion is 0.372.  At an inlet flowrate of 
152.2 mol ethylbenzene/s and a steam flowrate of 10 times the molar flowrate of ethylbenzene 
the conversion increases to 0.723.   
 
Once you have calculated Kp as a function of temperature, then you can enter this data into a 
table for the reaction rate.   
 
Hand Calculations for Keq 
 6


Procedure to Install a Reaction Rate with an Equilibrium Constant – Simple 
Reaction Rates 
 
1. Start HYSYS 
2. Since these 
compounds are 
hydrocarbons, use 
the Peng-
Robinson 
thermodynamic 
package.  
(Additional 
information on HYSYS thermodynamics packages 
can be found in the Simulation Basis Manual 
Appendix A: Property Methods and Calculatio
Note an alternative package for this system is the 
ns. 
3. 
 
n this list then use the Sort List… button 
4. 
 window and selecting Basis Manager from 
6. ss 
asis Manual for 
7. 
 
. In the Stoich Coeff field enter -1 (i.e. 1 moles of ethylbenzene will be 
 define the rest of the Stoichiometry tab as shown
9. 
Press here to 
start adding 
rxns 
PRSV)  
Install the chemicals for a styrene reactor:  
ethylbenzene, styrene, hydrogen and water.  If they
are not o
feature. 
Now return to the Simulation Basis Manager by 
selecting the Rxns tab and pressing the Simulation 
Basis Mgr… button or close the Fluid Package 
Basis-1
the menu. 
5. To install a reaction, press the Add Rxn button.  
From the Reactions view, highlight the Simple Rate reaction type and pre
the Add Reaction button.  Refer to Section 4.4 of the Simulation B
information concerning reaction types and the addition of reactions.  
On the Stoichiometry tab select the first row of the Component column in 
Stoichiometry Info matrix. Select ethylbenzene from the drop down list in the 
Edit Bar. The Mole Weight column should automatically provide the molar weight of
ethylbenzene
consumed).  
8. Now  in the adjacent figure.   
Go to Basis tab and set the Basis as partial pressure, the base component as ethylbenzene and 
 9
have the reaction take place only in the vapor phase.   
10. The pressure basis units should be atm and the units of the reaction rate given by equation 24 
11. b and enter the activation energy from equation 2 is 
is mol/(L s).  Since the status bar at the bottom of the property view shows Not Ready, then 
go to the Parameters tab.    
 Next go to the Parameters ta
molcalEa 21874= .  Convert the pre-exponential from units of kPa to have unit
n be made later in this tutorial.  : 
(1kg 2146g10mol 3
2 −−
s of atm so 
that a comparison ca
 
)
atm sgcat 
mol20315
atm
Pa1001325.1
Pa1000
kPa1
kPa sL
mol5.200
L 10
m 1
m 0.445
m
m
m 445.0
mkgkPa sgcat 
10491.7
5
gas
gas
3
3
gas
3
gas
3
R
3
R
3
cat
3
cat
cat
cat
cat
=
×





=
















×=A
 (24) 
12. Leave β blank or place a zero in the cell.  Notice that you don’t enter the negative sign with 
13.  your equilibrium constant values, with units of atm, using the equation  
the pre-exponential.  
 Now you must regress
 ( ) ( ) DTTCTBAK +++= lnln   (25) 
14. Below is the data table that is produced using the integrated van’t Hoff expression shown in 
10
7.92
550 1.10E-05
600 9.99E-05
650 6.46E-04
700 3.20E-03
750 0.013
775 0.024
800 0.043
810 0.054
820 0.067
830 0.082
840 0.101
850 0.124
860 0.151
870 0.183
880 0.221
890 0.266
900 0.318
910 0.379
920 0.450
930 0.532
950 0.736
970 1.003
990 1.348
010 1.791
1030 2.351
1050 3.051
equation 14.  These data can either be regressed using Microsoft Excel’s multiple linear 
Regression or a nonlinear regression program such as polymath.  
Make sure that the units of Kp are the same as your basis units.   
 
 
T (K) Kp (atm) 
500 E-07
1
 
 
 
Enter 
Simulation 
Environment 
Add to FP (Fluid 
Package) 
 
15. The results of the 
regression of the 
predicted K values with 
the HYSYS equilibrium 
constant equation 25 are 
shown in the adjacent 
table.  Add these 
constants to the Simple 
Rate window.  Make sure 
you add many significant 
digits!  
16. Name this reaction from 
Rxn-1 to Hermann eq.  
Close the Simple Rate Window after observing the green Ready symbol. 
  Coefficients 
A’ -13.2117277
B’ -13122.4699
C’ 4.353627619
D’ -0.00329709
17. By default, the Global Rxn Set is present within the Reaction Sets group when you first 
display the Reaction Manager. However, for this procedure, a new Reaction Set will be 
created. Press the Add Set button. HYSYS provides the name Set-1 and opens the Reaction 
Set property view.  
18. To attach the newly created Reaction to the Reaction Set, place the cursor in the  
cell under Active List.  
19. Open the drop down list in the Edit Bar and select the name of the Reaction. The Set Type 
will correspond to the type of Reaction that you have added to the Reaction Set. The status 
message will now display Ready. (Refer to Section 4.5 – Reaction Sets for details concerning Reactions 
Sets.) 
20. Press the Close button to return to 
the Reaction Manager. 
21. To attach the reaction set to the 
Fluid Package (your Peng 
Robinson thermodynamics), 
highlight Set-1 in the Reaction Sets 
group and press the Add to FP 
button. When a Reaction Set is 
 11
attached to a Fluid Package, it becomes available to unit operations within the 
Flowsheet using that particular Fluid Package.  
22. The Add ’Set-1’ view appears, from which you highlight a Fluid Package and 
press the Add Set to Fluid Package button.  
23. Press the Close button. Notice that the name of the Fluid Package (Basis-1) 
appears in the Assoc. Fluid Pkgs group when the Reaction Set is highlighted in 
the Reaction Sets group. 
PFR
24. Now Enter the Simulation Environment by pressing the button in the lower 
right hand portion  
25. Install a PFR reactor.  Either through the 
25.1. Flowsheet, Add operation 
25.2. f12 
25.3. or icon pad.  Click on PFR, then release left mouse button.  Move 
cursor to pfd screen and press left mouse button. Double click on the 
reactor to open.  
26. Add stream names as shown.  
27. Next go to the Parameters portion of the 
Design window.  Click on the radio button 
next to the pressure drop calculation by 
the Ergun equation.  
28. Next add the reaction set by selecting the 
reactions tab and choosing Reaction Set 
from the drop down menu.  
29. Go to the Rating Tab.  Remember in the 
case of distillation columns, in which you 
had to specify the number of stages?  
Similarly with PFR’s you have to specify 
the volume.  In this case add the volume 
as 250 m3, 7 m length, and a void fraction 
of 0.445 as shown in the figure.   
 12
30. Return to the Reactions tab and modify the specifications for your catalyst to the density and 
particle size given on page 4.   
31. Go to the Design Tab and select heat transfer.  For this tutorial we will have an isothermal 
reactor so leave this unspecified.  
32. Close the PFR Reactor 
 13
 
33. Open the workbook 
 
34. Isn’t it strange that you can’t see the molar flowrate in the composition window?  Do you 
have a composition tab?  Let’s add the molar flowrates to the workbook windows.  Go to 
Workbook setup either by right clicking on a tab or choosing workbook setup form the menu. 
35. If you don’t have a composition tab then, press the Add button on the left side and add a 
material stream and rename it Compositions.   
36. In the Compositions workbook tab, select Component Molar Flow and then press the All 
radio button.  
37. To change the units of the variables go 
to Tools, preferences 
38. Then either bring in a previously 
named preference set or go to the 
variables tab and clone the SI set and 
give this new set a name.   
Button 
39. Change the component molar flowrate 
units from kmol/hr to gmol/s. 
40. Change the Flow units from kmol/hr 
to gmol/s 
Give it a new 
name such as 
Compositions41. Next change the Energy from kJ/hr 
to kJ/s. Add 
42. Save preference set as well as the case.  
Remember that you need to open this 
preference set every time you use this 
case. 
Workbook 
Comp 
Molar 
Flow
 
 14
Back to the Simulation 
43. Now add a feed composition of pure ethylbenzene at 152.2 gmol/s, 1522 gmol/s of water, 
880 K, and 1.378 bar.  Then set the outlet temperature to 880K to obtain an isothermal 
reactor.  Remember you can type the variable and then press the space bar and type or select 
the units.  
44. No the reactor should solve for the outlet concentrations.  Take a note of the pressure drop in 
the Design Parameters menu.  I got a pressure drop of 86.38 kPa.  Now change the length of 
the reactor to 8 m.  If you get the above message then your reactor has not converged and you 
need to make adjustments to get 
your reactor to converge (e.g. the 
product stream is empty!)  Now it 
is your task to reduce the pressure 
drop to an acceptable level.  What 
do you need to alter?  Refer to the 
Ergun Equation given by 
 ( )








+
−





 −
−= G
DD
GP
pp
75.111501
dz
d
3
µφ
φ
φ
ρ
 (26) 
Using the Adjust Unit Operation 
Adjust 
45. Obtain a solution that will meet the following pressure drop specification   One 
way of doing this quickly is to use the adjust function.  Go to Flowsheet, Add operation (or 
press f12 or the green A in 
a diamond on the object 
palette.   
01.0 PP ≤∆
46. Now select the adjusted 
variable as the tube length 
and the target variable as 
the Pressure Drop.  Set the 
pressure drop to 13.78 kPa 
(exactly 10% of P0).   
 15
47. Next go to the Parameters tab 
and set the tolerance, step 
size and maximum iterations.  
If you have problems you can 
always press the Ignored 
button in the lower right hand 
corner of the page, then go 
back to the reactor and 
change the values by hand. If 
it stops, it may ask you if you 
want to continue.  Answer 
yes.  You can watch the 
stepping progress by going to 
the monitor tab. 
48. Try this again, but this time get your pressure 
drop to 1% of P0.  
49. Now turn this Adjust unit off by 
clicking on the ignored button. 
 
Examine Equilibrium Results at 
Large Reactor Volumes 
50. You equilibrium conversion 
should be around 72.6%.  
Comparing this to the hand 
calculated results for a steam to 
hydrocarbon molar ratio of 10 is 
72.3% at 880 and 137.8kPa. 
51. Set your pressure drop to zero by 
turning off the Ergun equation in 
the Reactor, Design Tab, 
Parameters option.  Set the 
pressure drop to zero.  The 
conversion is now 72.5%!  Which 
again is very close to your hand 
calculations.  
Ignored 
button 
 16
Now set the feed flowrate of steam to zero.  You should get a conversion of 37.4%. This 
again is what your spreadsheet 
calculation shows for 880K and 
137.8 kPa.  
52. How do you know that you have 
reached the equilibrium conversion 
that is limiting this reaction?  M
a plot of the molar flowrate of 
ethylbenzene using the tool in the 
performance tab and com
option of the reactor.  
ake 
position 
53. Next, make a plot of conversion as 
a function of both reactor 
temperature and pressure.  
Becareful how you set up this 
databook.  I had 943 data states by 
varying both 
 and 
.  Remember 
that you have to setup a workbook so that 
you only need to specify the temperature in 
one cell.  I would suggest that you add a 
spreadsheet to keep all of your calculations 
in one area.
kPaPkPa 500100 ≤≤
KTK 1050500 ≤≤
 17
 
54. Now make a plot of the effect of steam flow and temperature on conversion.  You will need 
to add a new feed stream to the 
reactor.   
54.1. Make your Feed stream 
have only 152.2 mol of 
ethylbenzene per second. 
18
54.2. Make a second feed 
steam called water have a flow 
of 0 mol/s.  Create a second cell 
in your spreadsheet that you can 
export the temperature to the 
Water feed stream temperature 
as well as the outlet stream, 
Product, to make the reactor 
isothermal and to the.  
Notice that you had to 
specify one cell for each 
export. 
54.3. Reorder your 
workbook by going into 
the menu for the 
workbook and choosing 
order/hide/reveal 
Objects.  Then put the 
water stream next to the 
feed stream. 
54.4. In the Data book 
bring in the following 
variables so that the 
 
water molar flow will be considered an independent variable.  (don’t do the number of 
states in these examples!) 
 
 
 
 19
 
General 
Reactors 
Equilibrium 
Reactors Equilibrium 
Reactor 
55.  Now we will 
install a 
second reactor 
that only 
contains an 
equilibrium 
reaction.  Use 
either the 
object palette 
or the Flowsheet, Add 
Operation, Equilibrium 
Reactor. 
56. Label the streams as shown 
57. Notice that in Red is a 
warning that it needs a 
reaction set.  Let’s see if it 
likes the one we already 
have.  Pull in the reaction 
being used by the PFR.  
Whoops!  It didn’t like this 
one!  Equilibrium reactors 
can only have equilibrium 
reactions.  We will have to 
create a new one. 
58. Click on the Erlenmeyer flask or choose Simulation, 
Enter Basis Environment. 
59. Add a new reaction.   
60. Go to the Library tab and choose the library reaction.  
Wow it was in there all the time!   
 20
61. Look at the Keq page.A plot of the data 
given in the HYSYS table and the 
equation that HYSYS uses to fit the data is 
given below. This comparison shows that 
the hand calculations and the HYSYS 
stored values are in good agreement with 
each other in the temperature range of 
.  Above 920 K the v
of K begin to deviate from each other. 
K 920500 ≤≤ T alues 
62. Attach the equilibrium reaction to a new 
11.  
or 
63. Return to the reactor using the green arrow 
ou 
t.  
t 
64.  the 
Go back to pfd or leave basis reaction set starting with step 17 on page 
(The step 17 is a hyperlink and is active in 
adobe.) Title the new set Equilibrium React
Set.  When finished return to the step 63.   
environment 
and bring in the new reaction set to the 
equilibrium reactor.  Now you see why y
need in some cases more than one reaction se
Another reason is that you may want one se
of reactions for a dehydrogenation reactor and 
then a separate set for an oxidation reactor. 
 Bring in the equilibrium reaction set into
reactor 
 21
65. Now specify the EQ Feed stream to be identical to the Feed stream.  This can be done by 
double clicking on the EQ Feed title or name.  And then choosing the Define from Other 
Stream… option. 
 
 
 
66. Define the temperature of one outlet stream to be equal to the feed.  Examine the following 2 
conditions from your PFR simulations at 880 K and 1.378 bar with: 
Cases HYSYS Library Hand Calculations 
0
2.152
0
=
=
steam
EB
F
smolF
 
2595.0
03.40
=
=
K
χ
 221.0
4.37
=
=
K
χ
 
smolF
smolF
steam
EB
1522
2.152
0
=
=
 
2595.0
95.74
=
=
K
χ
 2595.0
5.72
=
=
K
χ
 
 
Result for 
no steam 
flow 
 22
 
67.   Now add the values from your hand calculation into the equilibrium reactor.  Go to view 
reaction and enter these values within the reactor’s reaction tab.  Within the equilibrium 
reaction choose the basis tab and select the Ln(Keq) 
Equation:    Coefficients 
A -13.2117277
B -13122.4699
C 4.353627619
D -0.00329709
68.  Next enter the following table of coefficients for this 
equation 
69. Now rerun the above cases.  This will predict the PFR 
equilibrium values given in the table below. 
Cases HYSYS 
Library 
Hand 
Calculations 
Regression 
from Hand 
Calculations
0
2.152
0
=
=
steam
EB
F
smolF
 
2595.0
03.40
=
=
K
χ
 221.0
4.37
=
=
K
χ
 
221.0
4.37
=
=
K
χ
 
smolF
smolF
steam
EB
1522
2.152
0
=
=
 
2595.0
95.74
=
=
K
χ
 221.0
5.72
=
=
K
χ
 
221.0
5.72
=
=
K
χ
 
Notice that with the PFR you need a large volume or mass of catalyst to achieve these 
equilibrium values.  You previously tried this with your PFR and you came close to these above 
values.  In step 51 on page 16 your PFR values were 37.42 and 72.5%.   
70. Which values are correct?  Since, no reference is given by HYSYS to the library reaction and 
you know the source of the hand calculations3 you should trust your hand calculations.  
 23
 
Minimization of Gibbs Free Energy 
71. Go back to the reaction screen and choose the 
Gibbs Free Energy radio button. 
72. You get a conversion of 74.80 and K=0.2569.  In an 
older version of HYSYS you mistakenly got 100% 
conversion.  In the Gibbs Free energy minimization, 
the equilibrium constant is determined from the 
Ideal Gas Gibbs Free Energy Coefficients in the 
HYSYS library. 
 
73. ne th
73.1  basis 
73.3  styrene and view the 
mpo
73.4 e 
s 
 
l 
 
e!  
to 
investigate what it is doing.  
 
 Exami ese values.   
. Enter the
environment.  
73.2. View the property package 
. Select
co nent  
. Choose the temperatur
dependent tab: Tdep.  In the 
current version of HYSYS the 
temperature dependent propertie
of Styrene are given for all the 
ideal gas properties.  In an old
version of HYSYS, only one 
coefficient was given for the Idea
Gas Gibbs Free Energy.  In this
case the Ideal Gas Gibbs Free Energy was a constant and independent of temperatur
This was incorrect.  In the previous version new values were obtained from Aaron 
Pollock of Hyprotech Technical Support.4  This is a clear example of why you need 
critically examine the results produced by a process simulator!  You always need to 
Old 
Version:  
100%
 24
View 
Component 
 
 
Old
Version
G=constant
 
74. To modify properties you must create a hypothetical component that can either be a clone of 
ations 
Gib
 reactor called a Gibbs Reactor 
76. Put in the conditions given in step 65 on page 22 
nergy results.  The only difference for this reactor is 
a current chemical or an entirely new hypothetical 
component in which the properties are estimated 
using standard and proprietary methods.  See the 
Adobe pdf help manual:  Simulation Guide 
Chapter 3.  (go to the link in the reaction 
engineering homepage) Many of the estim
are based on the UNIFAC structure which is 
described in section 3.4.3 of that chapter.   
bs Reactor 
75. Now install a 3rd
and label the streams and define the feed and 
outlet temperature of the streams. 
above.  Notice that the same result as an 
equilibrium reactor using the gibbs free e
that you did not need to specify the stoichiometry of the reaction.  
 25
 
Submission: 
At the end of this exercise submit  
1) The following graphs from PFR  
a) the effect of temperature and pressure on equilibrium conversion (see step 53) 
b) the effect of the molar flow of steam and temperature on equilibrium conversion at a 
fixed pressure and ethylbenzene flowrate (see step 54). 
c) Short summary of the effect of T, P and steam flow on equilibrium conversion. 
2) Pfd of the three reactors 
 
 26
                                                
References: 
 
1 Hermann, Ch.; Quicker, P.; Dittmeyer, R., “Mathematical simulation of catalytic dehydrogenation of ethylbenzene 
to styrene in a composite palladium membrane reactor.”  J. Membr. Sci.  (1997),  136(1-2),  161-172. 
2 Fogler, H. S. Elements of Chemical Reaction Engineering, 3rd Ed., by, Prentice Hall PTR, Englewood Cliffs, NJ 
(1999).   
3 "Thermodynamics Source Database" by Thermodynamics Research Center, NIST Boulder Laboratories, M. 
Frenkel director, in NIST Chemistry WebBook, NIST Standard Reference Database Number 69, Eds. P.J. Linstrom 
and W.G. Mallard, July 2001, National Institute of Standards and Technology, Gaithersburg MD, 20899 
(http://webbook.nist.gov). 
4 Yaws, C.L. and Chiang, P.Y., "Find Favorable Reactions Faster", Hydrocarbon Processing, November 1988, pg 
81-84.