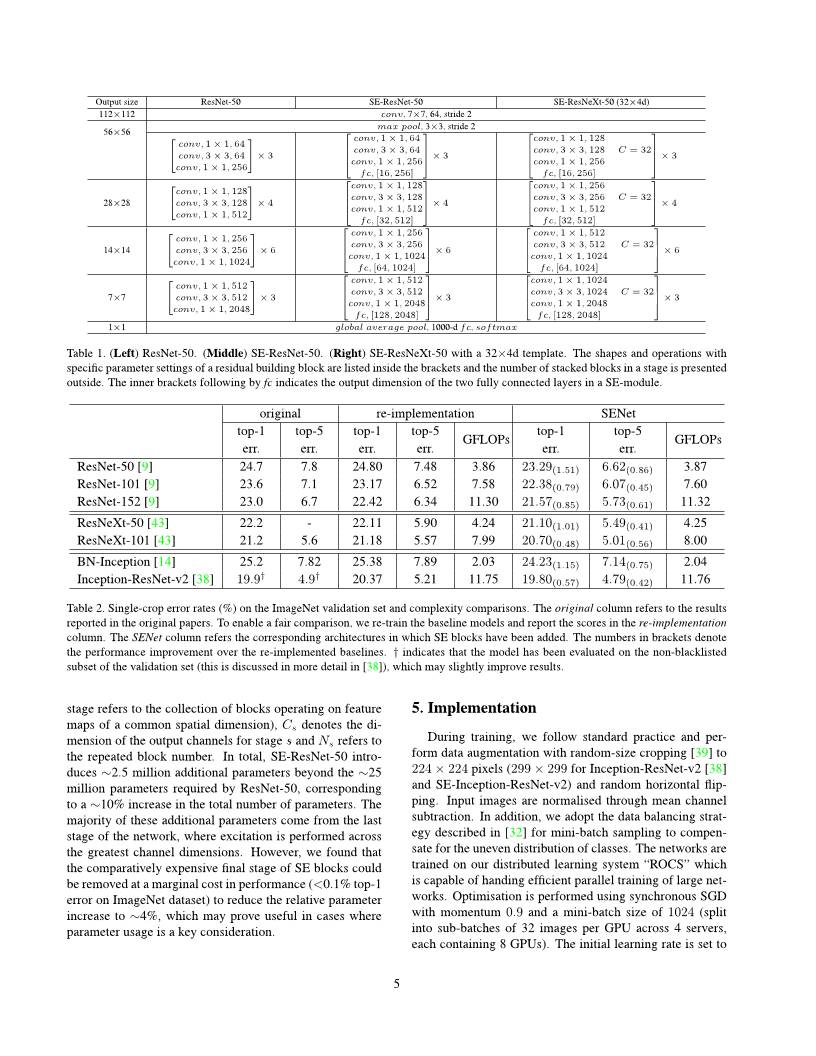
2017-SZNet.pdf
- 文件大小: 1.24MB
- 文件类型: pdf
- 上传日期: 2025-08-23
- 下载次数: 0
概要信息:
Squeeze-and-Excitation Networks Jie Hu∗ Momenta hujie@momenta.ai Li Shen∗ University of Oxford lishen@robots.ox.ac.uk Gang Sun∗ Momenta sungang@momenta.ai Abstract Convolutional neural networks are built upon the con- volution operation, which extracts informative features by fusing spatial and channel-wise information together within local receptive fields. In order to boost the representational power of a network, much existing work has shown the benefits of enhancing spatial encoding. In this work, we focus on channels and propose a novel architectural unit, which we term the “Squeeze-and-Excitation”(SE) block, that adaptively recalibrates channel-wise feature responses by explicitly modelling interdependencies between chan- nels. We demonstrate that by stacking these blocks to- gether, we can construct SENet architectures that gener- alise extremely well across challenging datasets. Crucially, we find that SE blocks produce significant performance im- provements for existing state-of-the-art deep architectures at slight computational cost. SENets formed the founda- tion of our ILSVRC 2017 classification submission which won first place and significantly reduced the top-5 error to 2.251%, achieving a ∼25% relative improvement over the winning entry of 2016. 1. Introduction Convolutional neural networks (CNNs) have proven to be effective models for tackling a variety of visual tasks [19, 23, 29, 41]. For each convolutional layer, a set of fil- ters are learned to express local spatial connectivity patterns along input channels. In other words, convolutional filters are expected to be informative combinations by fusing spa- tial and channel-wise information together, while restricted in local receptive fields. By stacking a series of convo- lutional layers interleaved with non-linearities and down- sampling, CNNs are capable of capturing hierarchical pat- terns with global receptive fields as powerful image descrip- tions. Recent work has demonstrated the performance of networks can be improved by explicitly embedding learning mechanisms that help capture spatial correlations without ∗Equal contribution. requiring additional supervision. One such approach was popularised by the Inception architectures [14, 39], which showed that the network can achieve competitive accuracy by embedding multi-scale processes in its modules. More recent work has sought to better model spatial dependence [1, 27] and incorporate spatial attention [17]. In contrast to these methods, we investigate a different aspect of architectural design - the channel relationship, by introducing a new architectural unit, which we term the “Squeeze-and-Excitation” (SE) block. Our goal is to im- prove the representational power of a network by explicitly modelling the interdependencies between the channels of its convolutional features. To achieve this, we propose a mech- anism that allows the network to perform feature recalibra- tion, through which it can learn to use global information to selectively emphasise informative features and suppress less useful ones. The basic structure of the SE building block is illustrated in Fig. 1. For any given transformation Ftr : X → U, X ∈ RW ′×H′×C′ ,U ∈ RW×H×C , (e.g. a convolution or a set of convolutions), we can construct a correspond- ing SE block to perform feature recalibration as follows. The features U are first passed through a squeeze opera- tion, which aggregates the feature maps across spatial di- mensions W × H to produce a channel descriptor. This descriptor embeds the global distribution of channel-wise feature responses, enabling information from the global re- ceptive field of the network to be leveraged by its lower lay- ers. This is followed by an excitation operation, in which sample-specific activations, learned for each channel by a self-gating mechanism based on channel dependence, gov- ern the excitation of each channel. The feature maps U are then reweighted to generate the output of the SE block which can then be fed directly into subsequent layers. An SE network can be generated by simply stacking a collection of SE building blocks. SE blocks can also be used as a drop-in replacement for the original block at any depth in the architecture. However, while the template for the building block is generic, as we show in Sec. 6.3, the role it performs at different depths adapts to the needs of the network. In the early layers, it learns to excite informative 1 ar X iv :1 70 9. 01 50 7v 1 [ cs .C V ] 5 S ep 2 01 7 Figure 1. A Squeeze-and-Excitation block. features in a class agnostic manner, bolstering the quality of the shared lower level representations. In later layers, the SE block becomes increasingly specialised, and responds to different inputs in a highly class-specific manner. Con- sequently, the benefits of feature recalibration conducted by SE blocks can be accumulated through the entire network. The development of new CNN architectures is a chal- lenging engineering task, typically involving the selection of many new hyperparameters and layer configurations. By contrast, the design of the SE block outlined above is sim- ple, and can be used directly with existing state-of-the-art architectures whose convolutional layers can be strength- ened by direct replacement with their SE counterparts. Moreover, as shown in Sec. 4, SE blocks are computation- ally lightweight and impose only a slight increase in model complexity and computational burden. To support these claims, we develop several SENets, namely SE-ResNet, SE- Inception, SE-ResNeXt and SE-Inception-ResNet and pro- vide an extensive evaluation of SENets on the ImageNet 2012 dataset [30]. Further, to demonstrate the general ap- plicability of SE blocks, we also present results beyond ImageNet, indicating that the proposed approach is not re- stricted to a specific dataset or a task. Using SENets, we won the first place in the ILSVRC 2017 classification competition. Our top performing model ensemble achieves a 2.251% top-5 error on the test set. This represents a ∼25% relative improvement in comparison to the winner entry of the previous year (with a top-5 error of 2.991%). Our models and related materials have been made available to the research community1. 2. Related Work Deep architectures. A wide range of work has shown that restructuring the architecture of a convolutional neural network in a manner that eases the learning of deep fea- tures can yield substantial improvements in performance. VGGNets [35] and Inception models [39] demonstrated the benefits that could be attained with an increased depth, sig- nificantly outperforming previous approaches on ILSVRC 2014. Batch normalization (BN) [14] improved gradient 1https://github.com/hujie-frank/SENet propagation through deep networks by inserting units to regulate layer inputs stabilising the learning process, which enables further experimentation with a greater depth. He et al. [9, 10] showed that it was effective to train deeper networks by restructuring the architecture to learn residual functions through the use of identity-based skip connections which ease the flow of information across units. More re- cently, reformulations of the connections between network layers [5, 12] have been shown to further improve the learn- ing and representational properties of deep networks. An alternative line of research has explored ways to tune the functional form of the modular components of a net- work. Grouped convolutions can be used to increase car- dinality (the size of the set of transformations) [13, 43] to learn richer representations. Multi-branch convolutions can be interpreted as a generalisation of this concept, en- abling more flexible compositions of convolutional opera- tors [14, 38, 39, 40]. Cross-channel correlations are typ- ically mapped as new combinations of features, either in- dependently of spatial structure [6, 18] or jointly by using standard convolutional filters [22] with 1× 1 convolutions, while much of this work has concentrated on the objective of reducing model and computational complexity. This ap- proach reflects an assumption that channel relationships can be formulated as a composition of instance-agnostic func- tions with local receptive fields. In contrast, we claim that providing the network with a mechanism to explicitly model dynamic, non-linear dependencies between channels using global information can ease the learning process, and signif- icantly enhance the representational power of the network. Attention and gating mechanisms. Attention can be viewed, broadly, as a tool to bias the allocation of available processing resources towards the most informative compo- nents of an input signal. The development and understand- ing of such mechanisms has been a longstanding area of research in the neuroscience community [15, 16, 28] and has seen significant interest in recent years as a powerful addition to deep neural networks [20, 25]. Attention has been shown to improve performance across a range of tasks, from localisation and understanding in images [3, 17] to sequence-based models [2, 24]. It is typically implemented in combination with a gating function (e.g. a softmax or 2 sigmoid) and sequential techniques [11, 37]. Recent work has shown its applicability to tasks such as image captioning [4, 44] and lip reading [7], in which it is exploited to effi- ciently aggregate multi-modal data. In these applications, it is typically used on top of one or more layers represent- ing higher-level abstractions for adaptation between modal- ities. Highway networks [36] employ a gating mechanism to regulate the shortcut connection, enabling the learning of very deep architectures. Wang et al. [42] introduce a powerful trunk-and-mask attention mechanism using an hourglass module [27], inspired by its success in semantic segmentation. This high capacity unit is inserted into deep residual networks between intermediate stages. In contrast, our proposed SE-block is a lightweight gating mechanism, specialised to model channel-wise relationships in a com- putationally efficient manner and designed to enhance the representational power of modules throughout the network. 3. Squeeze-and-Excitation Blocks The Squeeze-and-Excitation block is a computational unit which can be constructed for any given transforma- tion Ftr : X → U, X ∈ RW ′×H′×C′ ,U ∈ RW×H×C . For simplicity of exposition, in the notation that follows we take Ftr to be a standard convolutional operator. Let V = [v1,v2, . . . ,vC ] denote the learned set of filter ker- nels, where vc refers to the parameters of the c-th filter. We can then write the outputs of Ftr as U = [u1,u2, . . . ,uC ] where uc = vc ∗X = C′∑ s=1 vs c ∗ xs. (1) Here ∗ denotes convolution, vc = [v1 c ,v 2 c , . . . ,v C′ c ] and X = [x1,x2, . . . ,xC′ ] (to simplify the notation, bias terms are omitted). Here vs c is a 2D spatial kernel, and therefore represents a single channel of vc which acts on the corre- sponding channel of X. Since the output is produced by a summation through all channels, the channel dependen- cies are implicitly embedded in vc, but these dependencies are entangled with the spatial correlation captured by the filters. Our goal is to ensure that the network is able to in- crease its sensitivity to informative features so that they can be exploited by subsequent transformations, and to suppress less useful ones. We propose to achieve this by explicitly modelling channel interdependencies to recalibrate filter re- sponses in two steps, squeeze and excitation, before they are fed into next transformation. A diagram of an SE building block is shown in Fig. 1. 3.1. Squeeze: Global Information Embedding In order to tackle the issue of exploiting channel depen- dencies, we first consider the signal to each channel in the output features. Each of the learned filters operate with a local receptive field and consequently each unit of the trans- formation output U is unable to exploit contextual informa- tion outside of this region. This is an issue that becomes more severe in the lower layers of the network whose re- ceptive field sizes are small. To mitigate this problem, we propose to squeeze global spatial information into a channel descriptor. This is achieved by using global average pooling to generate channel-wise statistics. Formally, a statistic z ∈ RC is gen- erated by shrinking U through spatial dimensions W ×H , where the c-th element of z is calculated by: zc = Fsq(uc) = 1 W ×H W∑ i=1 H∑ j=1 uc(i, j). (2) Discussion. The transformation output U can be in- terpreted as a collection of the local descriptors whose statistics are expressive for the whole image. Exploiting such information is prevalent in feature engineering work [31, 34, 45]. We opt for the simplest, global average pool- ing, while more sophisticated aggregation strategies could be employed here as well. 3.2. Excitation: Adaptive Recalibration To make use of the information aggregated in the squeeze operation, we follow it with a second operation which aims to fully capture channel-wise dependencies. To fulfil this objective, the function must meet two criteria: first, it must be flexible (in particular, it must be capable of learning a nonlinear interaction between channels) and second, it must learn a non-mutually-exclusive relationship as multi- ple channels are allowed to be emphasised opposed to one- hot activation. To meet these criteria, we opt to employ a simple gating mechanism with a sigmoid activation: s = Fex(z,W) = σ(g(z,W)) = σ(W2δ(W1z)), (3) where δ refers to the ReLU [26] function, W1 ∈ RC r ×C and W2 ∈ RC×C r . To limit model complexity and aid general- isation, we parameterise the gating mechanism by forming a bottleneck with two fully-connected (FC) layers around the non-linearity, i.e. a dimensionality-reduction layer with parameters W1 with reduction ratio r (we set it to be 16, and this parameter choice is discussed in Sec. 6.3), a ReLU and then a dimensionality-increasing layer with parameters W2. The final output of the block is obtained by rescaling the transformation output U with the activations: x̃c = Fscale(uc, sc) = sc · uc, (4) where X̃ = [x̃1, x̃2, . . . , x̃C ] and Fscale(uc, sc) refers to channel-wise multiplication between the feature map uc ∈ RW×H and the scalar sc. 3 Inception Global pooling FC SE-Inception Module FC 1×1×C 1×1×C# X Inception X$ Inception Module X X$ Sigmoid 1×1×C 1×1×C Scale W ×&×C W ×&×C ReLU 1×1×C# Figure 2. The schema of the original Inception module (left) and the SE-Inception module (right). SE-ResNetModule + Global pooling FC FC + ResNet Module X X$ X X$ Sigmoid 1×1×C 1×1×C# 1×1×C 1×1×C Scale W ×&×C W ×&×C W ×&×C Residual Residual ReLU 1×1×C# Figure 3. The schema of the original Residual module (left) and the SE-ResNet module (right). Discussion. The activations act as channel weights adapted to the input-specific descriptor z. In this regard, SE blocks intrinsically introduce dynamics conditioned on the input, helping to boost feature discriminability. 3.3. Exemplars: SE-Inception and SE-ResNet The flexibility of the SE block means that it can be di- rectly applied to transformations beyond standard convolu- tions. To illustrate this point, we develop SENets by in- tegrating SE blocks into two popular network families of architectures, Inception and ResNet. SE blocks are con- structed for the Inception network by taking the transfor- mation Ftr to be an entire Inception module (see Fig. 2). By making this change for each such module in the archi- tecture, we construct an SE-Inception network. Residual networks and their variants have shown to be highly effective at learning deep representations. We de- velop a series of SE blocks that integrate with ResNet [9], ResNeXt [43] and Inception-ResNet [38] respectively. Fig. 3 depicts the schema of an SE-ResNet module. Here, the SE block transformation Ftr is taken to be the non- identity branch of a residual module. Squeeze and excitation both act before summation with the identity branch. 4. Model and Computational Complexity An SENet is constructed by stacking a set of SE blocks. In practice, it is generated by replacing each original block (i.e. residual block) with its corresponding SE counterpart (i.e. SE-residual block). We describe the architecture of SE-ResNet-50 and SE-ResNeXt-50 in Table 1. For the proposed SE block to be viable in practice, it must provide an acceptable model complexity and com- putational overhead which is important for scalability. To illustrate the cost of the module, we take the compari- son between ResNet-50 and SE-ResNet-50 as an example, where the accuracy of SE-ResNet-50 is obviously supe- rior to ResNet-50 and approaching a deeper ResNet-101 network (shown in Table 2). ResNet-50 requires ∼3.86 GFLOPs in a single forward pass for a 224 × 224 pixel in- put image. Each SE block makes use of a global average pooling operation in the squeeze phase and two small fully connected layers in the excitation phase, followed by an inexpensive channel-wise scaling operation. In aggregate, SE-ResNet-50 requires ∼3.87 GFLOPs, corresponding to only a 0.26% relative increase over the original ResNet-50. In practice, with a training mini-batch of 256 images, a single pass forwards and backwards through ResNet-50 takes 190ms, compared to 209ms for SE-ResNet-50 (both timings are performed on a server with 8 NVIDIA Titan X GPUs). We argue that it is a reasonable overhead as global pooling and small inner-product operations are less opti- mised in existing GPU libraries. Moreover, due to its impor- tance for embedded device applications, we also benchmark CPU inference time for each model: for a 224×224 pixel in- put image, ResNet-50 takes 164ms, compared to 167ms for SE-ResNet-50. The small additional computational over- head required by the SE block is justified by its contribution to model performance (discussed in detail in Sec. 6). Next, we consider the additional parameters introduced by the proposed block. All additional parameters are con- tained in the two fully connected layers of the gating mech- anism, which constitute a small fraction of the total network capacity. More precisely, the number of additional parame- ters introduced is given by: 2 r S∑ s=1 Ns · Cs 2 (5) where r denotes the reduction ratio (we set r to 16 in all our experiments), S refers to the number of stages (where each 4 Output size ResNet-50 SE-ResNet-50 SE-ResNeXt-50 (32×4d) 112×112 conv, 7×7, 64, stride 2 56×56 max pool, 3×3, stride 2 conv, 1× 1, 64 conv, 3× 3, 64 conv, 1× 1, 256 × 3 conv, 1× 1, 64 conv, 3× 3, 64 conv, 1× 1, 256 fc, [16, 256] × 3 conv, 1× 1, 128 conv, 3× 3, 128 C = 32 conv, 1× 1, 256 fc, [16, 256] × 3 28×28 conv, 1× 1, 128 conv, 3× 3, 128 conv, 1× 1, 512 × 4 conv, 1× 1, 128 conv, 3× 3, 128 conv, 1× 1, 512 fc, [32, 512] × 4 conv, 1× 1, 256 conv, 3× 3, 256 C = 32 conv, 1× 1, 512 fc, [32, 512] × 4 14×14 conv, 1× 1, 256 conv, 3× 3, 256 conv, 1× 1, 1024 × 6 conv, 1× 1, 256 conv, 3× 3, 256 conv, 1× 1, 1024 fc, [64, 1024] × 6 conv, 1× 1, 512 conv, 3× 3, 512 C = 32 conv, 1× 1, 1024 fc, [64, 1024] × 6 7×7 conv, 1× 1, 512 conv, 3× 3, 512 conv, 1× 1, 2048 × 3 conv, 1× 1, 512 conv, 3× 3, 512 conv, 1× 1, 2048 fc, [128, 2048] × 3 conv, 1× 1, 1024 conv, 3× 3, 1024 C = 32 conv, 1× 1, 2048 fc, [128, 2048] × 3 1×1 global average pool, 1000-d fc, softmax Table 1. (Left) ResNet-50. (Middle) SE-ResNet-50. (Right) SE-ResNeXt-50 with a 32×4d template. The shapes and operations with specific parameter settings of a residual building block are listed inside the brackets and the number of stacked blocks in a stage is presented outside. The inner brackets following by fc indicates the output dimension of the two fully connected layers in a SE-module. original re-implementation SENet top-1 err. top-5 err. top-1 err. top-5 err. GFLOPs top-1 err. top-5 err. GFLOPs ResNet-50 [9] 24.7 7.8 24.80 7.48 3.86 23.29(1.51) 6.62(0.86) 3.87 ResNet-101 [9] 23.6 7.1 23.17 6.52 7.58 22.38(0.79) 6.07(0.45) 7.60 ResNet-152 [9] 23.0 6.7 22.42 6.34 11.30 21.57(0.85) 5.73(0.61) 11.32 ResNeXt-50 [43] 22.2 - 22.11 5.90 4.24 21.10(1.01) 5.49(0.41) 4.25 ResNeXt-101 [43] 21.2 5.6 21.18 5.57 7.99 20.70(0.48) 5.01(0.56) 8.00 BN-Inception [14] 25.2 7.82 25.38 7.89 2.03 24.23(1.15) 7.14(0.75) 2.04 Inception-ResNet-v2 [38] 19.9† 4.9† 20.37 5.21 11.75 19.80(0.57) 4.79(0.42) 11.76 Table 2. Single-crop error rates (%) on the ImageNet validation set and complexity comparisons. The original column refers to the results reported in the original papers. To enable a fair comparison, we re-train the baseline models and report the scores in the re-implementation column. The SENet column refers the corresponding architectures in which SE blocks have been added. The numbers in brackets denote the performance improvement over the re-implemented baselines. † indicates that the model has been evaluated on the non-blacklisted subset of the validation set (this is discussed in more detail in [38]), which may slightly improve results. stage refers to the collection of blocks operating on feature maps of a common spatial dimension), Cs denotes the di- mension of the output channels for stage s and Ns refers to the repeated block number. In total, SE-ResNet-50 intro- duces ∼2.5 million additional parameters beyond the ∼25 million parameters required by ResNet-50, corresponding to a ∼10% increase in the total number of parameters. The majority of these additional parameters come from the last stage of the network, where excitation is performed across the greatest channel dimensions. However, we found that the comparatively expensive final stage of SE blocks could be removed at a marginal cost in performance (<0.1% top-1 error on ImageNet dataset) to reduce the relative parameter increase to ∼4%, which may prove useful in cases where parameter usage is a key consideration. 5. Implementation During training, we follow standard practice and per- form data augmentation with random-size cropping [39] to 224× 224 pixels (299× 299 for Inception-ResNet-v2 [38] and SE-Inception-ResNet-v2) and random horizontal flip- ping. Input images are normalised through mean channel subtraction. In addition, we adopt the data balancing strat- egy described in [32] for mini-batch sampling to compen- sate for the uneven distribution of classes. The networks are trained on our distributed learning system “ROCS” which is capable of handing efficient parallel training of large net- works. Optimisation is performed using synchronous SGD with momentum 0.9 and a mini-batch size of 1024 (split into sub-batches of 32 images per GPU across 4 servers, each containing 8 GPUs). The initial learning rate is set to 5 0 20 40 60 80 100 epochs 15 20 25 30 35 40 45 50 55 60 To p- 1 er ro r ( % ) ResNet-50 train ResNet-50 val SE-ResNet-50 train SE-ResNet-50 val 0 20 40 60 80 100 epochs 15 20 25 30 35 40 45 50 55 60 To p- 1 er ro r ( % ) ResNet-152 train ResNet-152 val SE-ResNet-152 train SE-ResNet-152 val Figure 4. Training curves on ImageNet. (Left): ResNet-50 and SE-ResNet-50; (Right): ResNet-152 and SE-ResNet-152. 0 20 40 60 80 100 epochs 15 20 25 30 35 40 45 50 55 60 To p- 1 er ro r ( % ) ResNeXt-50 train ResNeXt-50 val SE-ResNeXt-50 train SE-ResNeXt-50 val 0 20 40 60 80 100 epochs 15 20 25 30 35 40 45 50 55 60 To p- 1 er ro r ( % ) Inception-ResNet-v2 train Inception-ResNet-v2 val SE-Inception-ResNet-v2 train SE-Inception-ResNet-v2 val Figure 5. Training curves on ImageNet. (Left): ResNeXt-50 and SE-ResNeXt-50; (Right): Inception-ResNet-v2 and SE-Inception- ResNet-v2. 0.6 and decreased by a factor of 10 every 30 epochs. All models are trained for 100 epochs from scratch, using the weight initialisation strategy described in [8]. 6. Experiments In this section we conduct extensive experiments on the ImageNet 2012 dataset [30] for the purposes: first, to ex- plore the impact of the proposed SE block for the basic networks with different depths and second, to investigate its capacity of integrating with current state-of-the-art net- work architectures, which aim to a fair comparison be- tween SENets and non-SENets rather than pushing the per- formance. Next, we present the results and details of the models for ILSVRC 2017 classification task. Furthermore, we perform experiments on the Places365-Challenge scene classification dataset [48] to investigate how well SENets are able to generalise to other datasets. Finally, we investi- gate the role of excitation and give some analysis based on experimental phenomena. 6.1. ImageNet Classification The ImageNet 2012 dataset is comprised of 1.28 mil- lion training images and 50K validation images from 1000 classes. We train networks on the training set and report the top-1 and the top-5 errors using centre crop evaluations on the validation set, where 224 × 224 pixels are cropped from each image whose shorter edge is first resized to 256 (299 × 299 from each image whose shorter edge is first resized to 352 for Inception-ResNet-v2 and SE-Inception- ResNet-v2). Network depth. We first compare the SE-ResNet against a collection of standard ResNet architectures. Each ResNet and its corresponding SE-ResNet are trained with identi- cal optimisation schemes. The performance of the differ- ent networks on the validation set is shown in Table 2, which shows that SE blocks consistently improve perfor- mance across different depths with an extremely small in- crease in computational complexity. 6 0 20 40 60 80 100 epochs 20 30 40 50 60 70 80 To p- 1 er ro r ( % ) BN-Inception train BN-Inception val SE-BN-Inception train SE-BN-Inception val Figure 6. Training curves of BN-Inception and SE-BN-Inception on ImageNet. Remarkably, SE-ResNet-50 achieves a single-crop top-5 validation error of 6.62%, exceeding ResNet-50 (7.48%) by 0.86% and approaching the performance achieved by the much deeper ResNet-101 network (6.52% top-5 error) with only half of the computational overhead (3.87 GFLOPs vs. 7.58 GFLOPs). This pattern is repeated at greater depth, where SE-ResNet-101 (6.07% top-5 error) not only matches, but outperforms the deeper ResNet-152 network (6.34% top-5 error) by 0.27%. Fig. 4 depicts the train- ing and validation curves of SE-ResNets and ResNets, re- spectively. While it should be noted that the SE blocks themselves add depth, they do so in an extremely compu- tationally efficient manner and yield good returns even at the point at which extending the depth of the base archi- tecture achieves diminishing returns. Moreover, we see that the performance improvements are consistent through train- ing across a range of different depths, suggesting that the improvements induced by SE blocks can be used in combi- nation with adding more depth to the base architecture. Integration with modern architectures. We next inves- tigate the effect of combining SE blocks with another two state-of-the-art architectures, Inception-ResNet-v2 [38] and ResNeXt [43]. The Inception architecture constructs mod- ules of convolutions as multibranch combinations of fac- torised filters, reflecting the Inception hypothesis [6] that spatial correlations and cross-channel correlations can be mapped independently. In contrast, the ResNeXt archi- tecture asserts that richer representations can be obtained by aggregating combinations of sparsely connected (in the channel dimension) convolutional features. Both ap- proaches introduce prior-structured correlations in modules. We construct SENet equivalents of these networks, SE- Inception-ResNet-v2 and SE-ResNeXt (the configuration of SE-ResNeXt-50 (32×4d) is given in Table 1). Like previ- ous experiments, the same optimisation scheme is used for both the original networks and their SENet counterparts. The results given in Table 2 illustrate the significant per- formance improvement induced by SE blocks when intro- duced into both architectures. In particular, SE-ResNeXt-50 has a top-5 error of 5.49% which is superior to both its direct counterpart ResNeXt-50 (5.90% top-5 error) as well as the deeper ResNeXt-101 (5.57% top-5 error), a model which has almost double the number of parame- ters and computational overhead. As for the experiments of Inception-ResNet-v2, we conjecture the difference of cropping strategy might lead to the gap between their re- ported result and our re-implemented one, as their orig- inal image size has not been clarified in [38] while we crop the 299 × 299 region from a relative larger image (where the shorter edge is resized to 352). SE-Inception- ResNet-v2 (4.79% top-5 error) outperforms our reimple- mented Inception-ResNet-v2 (5.21% top-5 error) by 0.42% (a relative improvement of 8.1%) as well as the reported result in [38]. The optimisation curves for each network are depicted in Fig. 5, illustrating the consistency of the improvement yielded by SE blocks throughout the training process. Finally, we assess the effect of SE blocks when operating on a non-residual network by conducting experiments with the BN-Inception architecture [14] which provides good performance at a lower model complexity. The results of the comparison are shown in Table 2 and the training curves are shown in Fig. 6, exhibiting the same phenomena that emerged in the residual architectures. In particular, SE-BN- Inception achieves a lower top-5 error of 7.14% in com- parison to BN-Inception whose error rate is 7.89%. These experiments demonstrate that improvements induced by SE blocks can be used in combination with a wide range of ar- chitectures. Moreover, this result holds for both residual and non-residual foundations. Results on ILSVRC 2017 Classification Competition. ILSVRC [30] is an annual computer vision competition which has proved to be a fertile ground for model devel- opments in image classification. The training and validation data of the ILSVRC 2017 classification task are drawn from the ImageNet 2012 dataset, while the test set consists of an additional unlabelled 100K images. For the purposes of the competition, the top-5 error metric is used to rank entries. SENets formed the foundation of our submission to the challenge where we won first place. Our winning entry comprised a small ensemble of SENets that employed a standard multi-scale and multi-crop fusion strategy to ob- tain a 2.251% top-5 error on the test set. This result repre- sents a∼25% relative improvement on the winning entry of 2016 (2.99% top-5 error). One of our high-performing net- works is constructed by integrating SE blocks with a modi- fied ResNeXt [43] (details of the modifications are provided in Appendix A). We compare the proposed architecture with 7 224× 224 320× 320 / 299× 299 top-1 err. top-5 err. top-1 err. top-5 err. ResNet-152 [9] 23.0 6.7 21.3 5.5 ResNet-200 [10] 21.7 5.8 20.1 4.8 Inception-v3 [40] - - 21.2 5.6 Inception-v4 [38] - - 20.0 5.0 Inception-ResNet-v2 [38] - - 19.9 4.9 ResNeXt-101 (64 × 4d) [43] 20.4 5.3 19.1 4.4 DenseNet-161 (k = 48) [12] 22.2 - - - Very Deep PolyNet [47] - - 18.71 4.25 DPN-131 [5] 19.93 5.12 18.55 4.16 SENet 18.68 4.47 17.28 3.79 Table 3. Single-crop error rates of state-of-the-art CNNs on ImageNet validation set. The size of test crop is 224 × 224 and 320 × 320 / 299× 299 as in [10]. Our proposed model, SENet, shows a significant performance improvement on prior work. top-1 err. top-5 err. Places-365-CNN [33] 41.07 11.48 ResNet-152 (ours) 41.15 11.61 SE-ResNet-152 40.37 11.01 Table 4. Single-crop error rates (%) on the Places365 validation set. Ratio r top-1 err. top-5 err. model size (MB) 4 23.21 6.63 137 8 23.19 6.64 117 16 23.29 6.62 108 32 23.40 6.77 103 original 24.80 7.48 98 Table 5. Single-crop error rates (%) on the ImageNet validation set and corresponding model sizes for the SE-ResNet-50 architecture at different reduction ratios r. Here original refers to ResNet-50. the state-of-the-art models on the ImageNet validation set in Table 3. Our model achieves a top-1 error of 18.68% and a top-5 error of 4.47% using a 224× 224 centre crop evalua- tion on each image (where the shorter edge is first resized to 256). To enable a fair comparison with previous models, we also provide a 320 × 320 centre crop evaluation, obtaining the lowest error rate under both the top-1 (17.28%) and the top-5 (3.79%) error metrics. 6.2. Scene Classification Large portions of the ImageNet dataset consist of im- ages dominated by single objects. To evaluate our proposed model in more diverse scenarios, we also evaluate it on the Places365-Challenge dataset [48] for scene classifica- tion. This dataset comprises 8 million training images and 36, 500 validation images across 365 categories. Relative to classification, the task of scene understanding can provide a better assessment of the ability of a model to generalise well and handle abstraction, since it requires the capture of more complex data associations and robustness to a greater level of appearance variation. We use ResNet-152 as a strong baseline to assess the ef- fectiveness of SE blocks and follow the evaluation protocol in [33]. Table 4 shows the results of training a ResNet-152 model and a SE-ResNet-152 for the given task. Specifically, SE-ResNet-152 (11.01% top-5 error) achieves a lower vali- dation error than ResNet-152 (11.61% top-5 error), provid- ing evidence that SE blocks can perform well on different datasets. This SENet surpasses the previous state-of-the- art model Places-365-CNN [33] which has a top-5 error of 11.48% on this task. 6.3. Analysis and Discussion Reduction ratio. The reduction ratio r introduced in Eqn. (5) is an important hyperparameter which allows us to vary the capacity and computational cost of the SE blocks in the model. To investigate this relationship, we conduct experiments based on the SE-ResNet-50 architecture for a range of different r values. The comparison in Table 5 reveals that performance does not improve monotonically with increased capacity. This is likely to be a result of en- abling the SE block to overfit the channel interdependen- cies of the training set. In particular, we found that set- ting r = 16 achieved a good tradeoff between accuracy and complexity and consequently, we used this value for all ex- periments. The role of Excitation. While SE blocks have been empir- ically shown to improve network performance, we would 8 (a) goldfish (b) pug (c) plane (d) cliff Figure 7. Example images from the four classes of ImageNet. also like to understand how the self-gating excitation mech- anism operates in practice. To provide a clearer picture of the behaviour of SE blocks, in this section we study exam- ple activations from the SE-ResNet-50 model and examine their distribution with respect to different classes at different blocks. Specifically, we sample four classes from the Ima- geNet dataset that exhibit semantic and appearance diver- sity, namely goldfish, pug, plane and cliff (example images from these classes are shown in Fig. 7). We then draw fifty samples for each class from the validation set and compute the average activations for fifty uniformly sampled chan- nels in the last SE block in each stage (immediately prior to downsampling) and plot their distribution in Fig. 8. For ref- erence, we also plot the distribution of average activations across all 1000 classes. We make the following three observations about the role of Excitation in SENets. First, the distribution across differ- ent classes is nearly identical in lower layers, e.g. SE 2 3. This suggests that the importance of feature channels is likely to be shared by different classes in the early stages of the network. Interestingly however, the second observation is that at greater depth, the value of each channel becomes much more class-specific as different classes exhibit differ- ent preferences to the discriminative value of features e.g. SE 4 6 and SE 5 1. The two observations are consistent with findings in previous work [21, 46], namely that lower layer features are typically more general (i.e. class agnostic in the context of classification) while higher layer features have greater specificity. As a result, representation learn- ing benefits from the recalibration induced by SE blocks which adaptively facilitates feature extraction and speciali- sation to the extent that it is needed. Finally, we observe a somewhat different phenomena in the last stage of the net- work. SE 5 2 exhibits an interesting tendency towards a saturated state in which most of the activations are close to 1 and the remainder are close to 0. At the point at which all activations take the value 1, this block would become a standard residual block. At the end of the network in the SE 5 3 (which is immediately followed by global pooling prior before classifiers), a similar pattern emerges over dif- ferent classes, up to a slight change in scale (which could be tuned by the classifiers). This suggests that SE 5 2 and SE 5 3 are less important than previous blocks in provid- ing recalibration to the network. This finding is consistent with the result of the empirical investigation in Sec. 4 which demonstrated that the overall parameter count could be sig- nificantly reduced by removing the SE blocks for the last stage with only a marginal loss of performance (< 0.1% top-1 error). 7. Conclusion In this paper we proposed the SE block, a novel architec- tural unit designed to improve the representational capacity of a network by enabling it to perform dynamic channel- wise feature recalibration. Extensive experiments demon- strate the effectiveness of SENets which achieve state-of- the-art performance on multiple datasets. In addition, they provide some insight into the limitations of previous archi- tectures in modelling channel-wise feature dependencies, which we hope may prove useful for other tasks requiring strong discriminative features. Finally, the feature impor- tance induced by SE blocks may be helpful to related fields such as network pruning for compression. Acknowledgements. We would like to thank Professor Andrew Zisserman for his helpful comments and Samuel Albanie for his discussions and writing edit for the paper. We would like to thank Chao Li for his contributions in the memory optimisation of the training system. Li Shen is supported by the Office of the Director of National Intel- ligence (ODNI), Intelligence Advanced Research Projects Activity (IARPA), via contract number 2014-14071600010. The views and conclusions contained herein are those of the author and should not be interpreted as necessarily rep- resenting the official policies or endorsements, either ex- pressed or implied, of ODNI, IARPA, or the U.S. Govern- ment. The U.S. Government is authorized to reproduce and distribute reprints for Governmental purpose notwithstand- ing any copyright annotation thereon. References [1] S. Bell, C. L. Zitnick, K. Bala, and R. Girshick. Inside- outside net: Detecting objects in context with skip pooling and recurrent neural networks. In CVPR, 2016. [2] T. Bluche. Joint line segmentation and transcription for end- to-end handwritten paragraph recognition. In NIPS, 2016. [3] C. Cao, X. Liu, Y. Yang, Y. Yu, J. Wang, Z. Wang, Y. Huang, L. Wang, C. Huang, W. Xu, D. Ramanan, and T. S. Huang. Look and think twice: Capturing top-down visual atten- tion with feedback convolutional neural networks. In ICCV, 2015. [4] L. Chen, H. Zhang, J. Xiao, L. Nie, J. Shao, W. Liu, and T. Chua. SCA-CNN: Spatial and channel-wise attention in convolutional networks for image captioning. In CVPR, 2017. [5] Y. Chen, J. Li, H. Xiao, X. Jin, S. Yan, and J. Feng. Dual path networks. arXiv:1707.01629, 2017. [6] F. Chollet. Xception: Deep learning with depthwise separa- ble convolutions. In CVPR, 2017. 9 (a) SE 2 3 (b) SE 3 4 (c) SE 4 6 (d) SE 5 1 (e) SE 5 2 (f) SE 5 3 Figure 8. Activations induced by Excitation in the different modules of SE-ResNet-50 on ImageNet. The module is named as “SE stageID blockID”. [7] J. S. Chung, A. Senior, O. Vinyals, and A. Zisserman. Lip reading sentences in the wild. In CVPR, 2017. [8] K. He, X. Zhang, S. Ren, and J. Sun. Delving deep into rec- tifiers: Surpassing human-level performance on ImageNet classification. In ICCV, 2015. [9] K. He, X. Zhang, S. Ren, and J. Sun. Deep residual learning for image recognition. In CVPR, 2016. [10] K. He, X. Zhang, S. Ren, and J. Sun. Identity mappings in deep residual networks. In ECCV, 2016. [11] S. Hochreiter and J. Schmidhuber. Long short-term memory. Neural computation, 1997. [12] G. Huang, Z. Liu, K. Q. Weinberger, and L. Maaten. Densely connected convolutional networks. In CVPR, 2017. [13] Y. Ioannou, D. Robertson, R. Cipolla, and A. Criminisi. Deep roots: Improving CNN efficiency with hierarchical fil- ter groups. In CVPR, 2017. [14] S. Ioffe and C. Szegedy. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In ICML, 2015. [15] L. Itti and C. Koch. Computational modelling of visual at- tention. Nature reviews neuroscience, 2001. [16] L. Itti, C. Koch, and E. Niebur. A model of saliency-based visual attention for rapid scene analysis. IEEE TPAMI, 1998. [17] M. Jaderberg, K. Simonyan, A. Zisserman, and K. Kavukcuoglu. Spatial transformer networks. In NIPS, 2015. [18] M. Jaderberg, A. Vedaldi, and A. Zisserman. Speeding up convolutional neural networks with low rank expansions. In BMVC, 2014. [19] A. Krizhevsky, I. Sutskever, and G. E. Hinton. ImageNet classification with deep convolutional neural networks. In NIPS, 2012. [20] H. Larochelle and G. E. Hinton. Learning to combine foveal glimpses with a third-order boltzmann machine. In NIPS, 2010. [21] H. Lee, R. Grosse, R. Ranganath, and A. Y. Ng. Convolu- tional deep belief networks for scalable unsupervised learn- ing of hierarchical representations. In ICML, 2009. 10 [22] M. Lin, Q. Chen, and S. Yan. Network in network. arXiv:1312.4400, 2013. [23] J. Long, E. Shelhamer, and T. Darrell. Fully convolutional networks for semantic segmentation. In CVPR, 2015. [24] A. Miech, I. Laptev, and J. Sivic. Learnable pooling with context gating for video classification. arXiv:1706.06905, 2017. [25] V. Mnih, N. Heess, A. Graves, and K. Kavukcuoglu. Recur- rent models of visual attention. In NIPS, 2014. [26] V. Nair and G. E. Hinton. Rectified linear units improve re- stricted boltzmann machines. In ICML, 2010. [27] A. Newell, K. Yang, and J. Deng. Stacked hourglass net- works for human pose estimation. In ECCV, 2016. [28] B. A. Olshausen, C. H. Anderson, and D. C. V. Essen. A neurobiological model of visual attention and invariant pat- tern recognition based on dynamic routing of information. Journal of Neuroscience, 1993. [29] S. Ren, K. He, R. Girshick, and J. Sun. Faster R-CNN: To- wards real-time object detection with region proposal net- works. In NIPS, 2015. [30] O. Russakovsky, J. Deng, H. Su, J. Krause, S. Satheesh, S. Ma, Z. Huang, A. Karpathy, A. Khosla, M. Bernstein, A. C. Berg, and L. Fei-Fei. ImageNet large scale visual recognition challenge. IJCV, 2015. [31] J. Sanchez, F. Perronnin, T. Mensink, and J. Verbeek. Im- age classification with the fisher vector: Theory and practice. RR-8209, INRIA, 2013. [32] L. Shen, Z. Lin, and Q. Huang. Relay backpropagation for effective learning of deep convolutional neural networks. In ECCV, 2016. [33] L. Shen, Z. Lin, G. Sun, and J. Hu. Places401 and places365 models. https://github.com/lishen-shirley/ Places2-CNNs, 2016. [34] L. Shen, G. Sun, Q. Huang, S. Wang, Z. Lin, and E. Wu. Multi-level discriminative dictionary learning with applica- tion to large scale image classification. IEEE TIP, 2015. [35] K. Simonyan and A. Zisserman. Very deep convolutional networks for large-scale image recognition. In ICLR, 2015. [36] R. K. Srivastava, K. Greff, and J. Schmidhuber. Training very deep networks. In NIPS, 2015. [37] M. F. Stollenga, J. Masci, F. Gomez, and J. Schmidhuber. Deep networks with internal selective attention through feed- back connections. In NIPS, 2014. [38] C. Szegedy, S. Ioffe, V. Vanhoucke, and A. Alemi. Inception- v4, inception-resnet and the impact of residual connections on learning. arXiv:1602.07261, 2016. [39] C. Szegedy, W. Liu, Y. Jia, P. Sermanet, S. Reed, D. Anguelov, D. Erhan, V. Vanhoucke, and A. Rabinovich. Going deeper with convolutions. In CVPR, 2015. [40] C. Szegedy, V. Vanhoucke, S. Ioffe, J. Shlens, and Z. Wojna. Rethinking the inception architecture for computer vision. In CVPR, 2016. [41] A. Toshev and C. Szegedy. DeepPose: Human pose estima- tion via deep neural networks. In CVPR, 2014. [42] F. Wang, M. Jiang, C. Qian, S. Yang, C. Li, H. Zhang, X. Wang, and X. Tang. Residual attention network for image classification. In CVPR, 2017. [43] S. Xie, R. Girshick, P. Dollar, Z. Tu, and K. He. Aggregated residual transformations for deep neural networks. In CVPR, 2017. [44] K. Xu, J. Ba, R. Kiros, K. Cho, A. Courville, R. Salakhudi- nov, R. Zemel, and Y. Bengio. Show, attend and tell: Neural image caption generation with visual attention. In ICML, 2015. [45] J. Yang, K. Yu, Y. Gong, and T. Huang. Linear spatial pyra- mid matching using sparse coding for image classification. In CVPR, 2009. [46] J. Yosinski, J. Clune, Y. Bengio, and H. Lipson. How trans- ferable are features in deep neural networks? In NIPS, 2014. [47] X. Zhang, Z. Li, C. C. Loy, and D. Lin. Polynet: A pursuit of structural diversity in very deep networks. In CVPR, 2017. [48] B. Zhou, A. Lapedriza, A. Khosla, A. Oliva, and A. Torralba. Places: A 10 million image database for scene recognition. IEEE TPAMI, 2017. A. ILSVRC 2017 Classification Competition Entry Details The SENet in Table 3 is constructed by integrating SE blocks to a modified version of the 64×4d ResNeXt-152 that extends the original ResNeXt-101 [43] by following the block stacking of ResNet-152 [9]. More differences to the design and training (beyond the use of SE blocks) were as follows: (a) The number of first 1×1 convolutional channels for each bottleneck building block was halved to reduce the computation cost of the network with a minimal decrease in performance. (b) The first 7× 7 convolutional layer was re- placed with three consecutive 3×3 convolutional layers. (c) The down-sampling projection 1× 1 with stride-2 convolu- tion was replaced with a 3 × 3 stride-2 convolution to pre- serve information. (d) A dropout layer (with a drop ratio of 0.2) was inserted before the classifier layer to prevent over- fitting. (e) Label-smoothing regularisation (as introduced in [40]) was used during training. (f) The parameters of all BN layers were frozen for the last few training epochs to ensure consistency between training and testing. (g) Training was performed with 8 servers (64 GPUs) in parallelism to enable a large batch size (2048) and initial learning rate of 1.0. 11
缩略图:
当前页面二维码






 工程招标采购
工程招标采购 搞笑表情
搞笑表情 微信头像
微信头像 美女图片
美女图片 APP小游戏
APP小游戏 PPT模板
PPT模板