概要信息：

第 章 晶体的微观对称性四
原子或原子团位置的对称性叫做微观对称性
宏观对称性 微观对称性晶体
3
微观对称性和宏观对称性的主要区别：
1 宏观对称性对称元素必须相交一点 微观对称性中、 ，
对称元素不须交于一点，可以在三维空间无限分布。
2、宏观对称性中对称元素只考虑方向，微观对称
性中需要考虑对称元素的相互位置关系。
4
点阵反映了晶体结构的周期性，这种周期性也就
是点阵的平移复原的特性。对于点阵，连接任意两
个阵点的位置矢量：
R= ma+ nb+ pc，
进行平移可以使点阵复原，表现在晶体结构上就是
使在三维空间无限伸展的相同部分得以重复 R可。
以定义为晶体微观结构平移的方向矢量。
微观对称元素 宏观对称元素= 
+ 平移 (平移轴、螺旋轴、滑移面) 
5
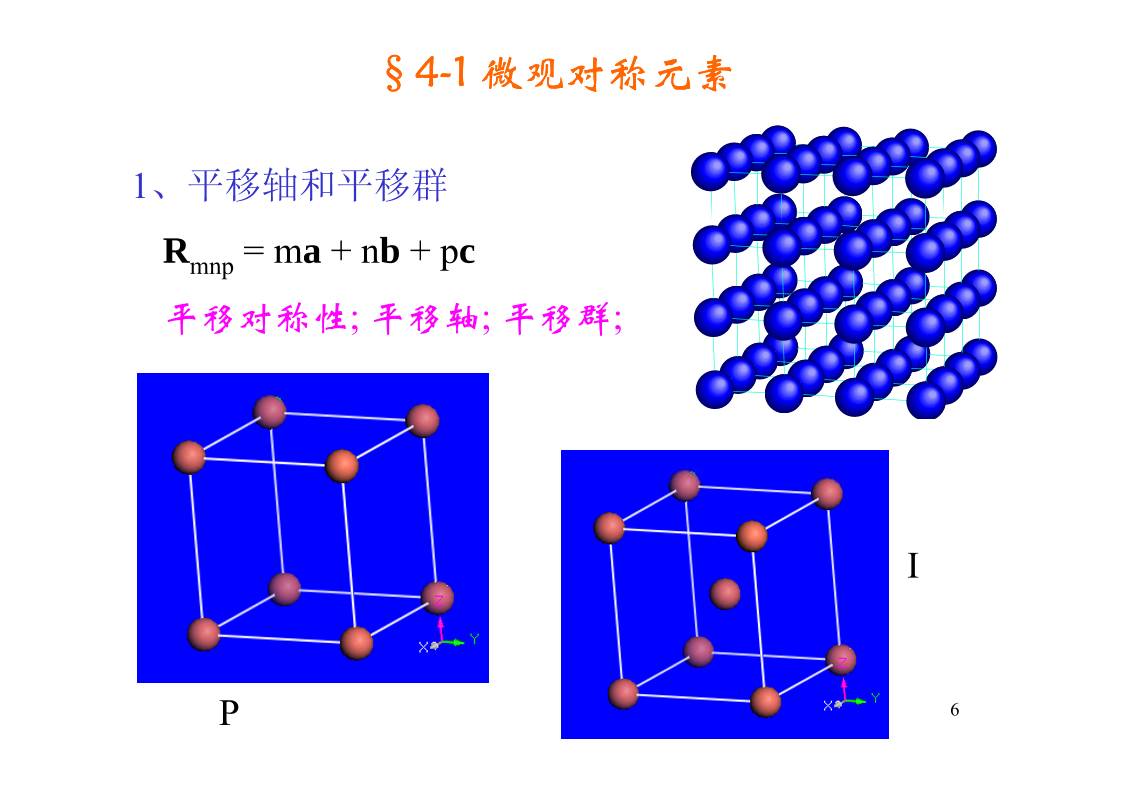
§4-1 微观对称元素
1、平移轴和平移群
Rmnp = ma + nb + pc
平移对称性 平移轴 平移群; ; ;
I
6P
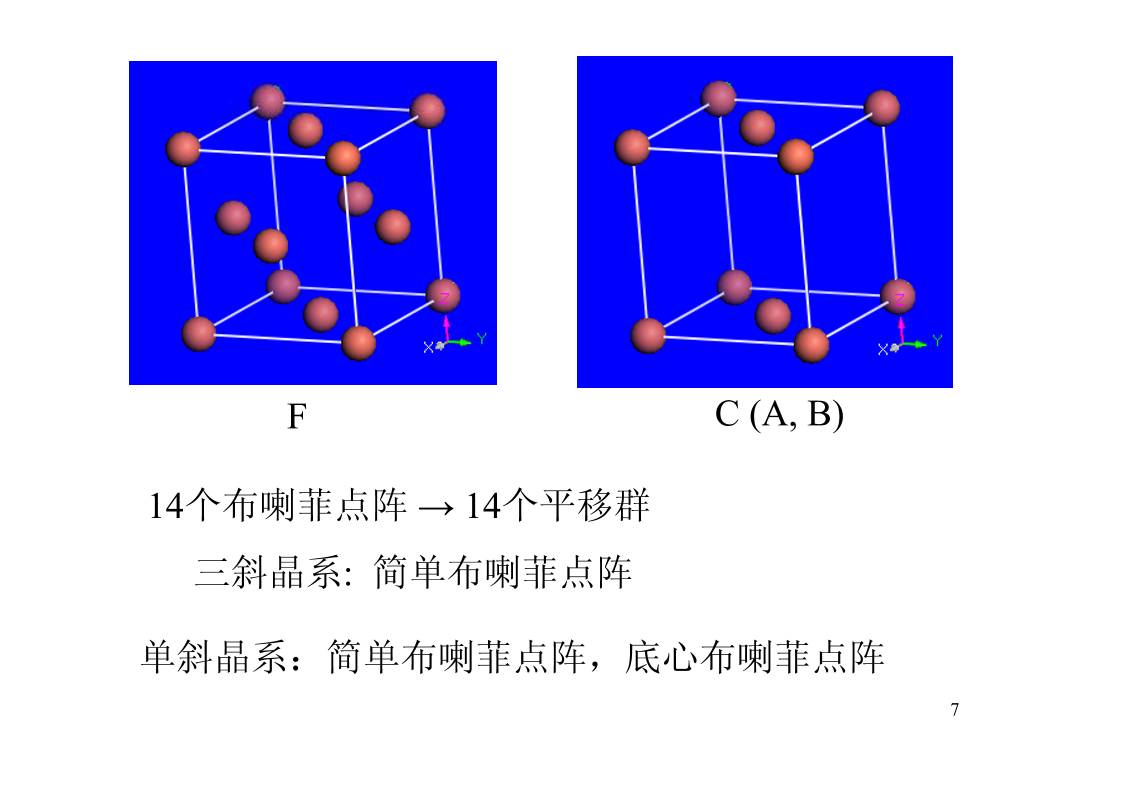
F C (A, B)
14个布喇菲点阵→ 14个平移群
三斜晶系: 简单布喇菲点阵  
单斜晶系：简单布喇菲点阵，底心布喇菲点阵
7
a' = a
b' = b
a' = a
b' = b
c' = a + c c' = （a + c）/2
正交晶系 简单 体心 面心和底心点阵： 、 、
四方晶系：体心和简单四方点阵
三角晶系：简单三角点阵
六角晶系：简单六角点阵
8立方晶系：简单、面心和体心立方点阵
2、螺旋对称轴
A: 41;  B: 43
金刚石
0,10,1 0.5
0 75
0.50.5
0.25
.
B
0.250.75
A0,1
0,10,1 0.5
9
螺旋轴 ns: 旋转 + 平移 
平移矢量: Tτ
n
s
   
    n=1, 2, 3, 4, 6;  
    s=0，1，2，... n-1 
10
（1）2次螺旋轴
n=2，s=0、1。
转轴s=0: =0，2次旋 ;
s=1: =T/2, 21螺旋轴。
T
1
2
11
（2）3次螺旋轴
0 
+
T
+
+
3
12
1 T 
3
+ 1
3
+ 2
+
3
31
13
2 T 
3
+ 2
3
1+
+
3
32
14
n=3
s=0 =0 3次旋转轴, ,
s=1, =T/3 , 31次螺旋轴, 右螺旋;
s=2,  =T/3 , 32次螺旋轴，左螺旋。
15
(3) 4次螺旋轴
n=4
s 0=  
+
T +
+
+
194
T
2
4
 
+
1
4
+
+
4
3
4
+
41
20
2 T 
4
+
1
+
+ 1
2
2
+
42
21
3 T
+2
4

4
3
+
+ 1
4
4
+
43
22
n 4
0 4次旋转轴
=
s= ， ；
1 1/4T 右螺旋轴4s= ,  τ= ， 1；
2 2/4T 中性螺旋轴4 双螺旋轴s= , τ= ， 2， ；
s=3 τ=3/4T 左螺旋轴4, ， 3。
23
（4）6次螺旋轴
6 6
0
1
=1/6T
 
=
24
62 6
=2/6T
3
=3/6T
 
25
64 65
=4/6T =5/6T
 
26

右61 ←→ 右65


27
n=6
=0: 6 次旋转轴； 
1/6T 6 右螺旋轴 = : 1, ;
 =2/6 T: 62, 右螺旋轴, 双轨螺旋轴; 
 =3/6 T: 63, 中性螺旋轴，3 轨螺旋轴;
 =4/6 T: 64 左螺旋轴 双轨螺旋轴;  , , 
 =5/6 T: 65, 左螺旋轴。 
s < n/2: 右螺旋轴； 
s = n/2: 中性螺旋轴；  
s>n/2: 左螺旋轴; 
次左螺旋轴等同于( )次右螺旋轴
28
s n-s 。
3、滑移面
- 105
-.105 .105 .395 .605 .895 1.105
.6051.105605
方硫镍矿 NiS2 
立方晶系 m3 .
.105
0 0.5
.895 .395
.
.395
a
 
.395
0 5
.395.895 -.105
.605
.5 .
.605 .1051.105
a
.895
1 105 0 0.5
.105.605 .605
. .395 -.105 .395
Ni S滑移 平移 + 反映
29
=  
沿着c轴滑移c/2,然后再对（100）面做反映
c(1) 轴滑移 
= a/2，b/2，c/2
a
b
轴滑移面, a、b或c
(2) 角滑移
a
= (a  b)/2，(b  c)/2，(a  c)/2 和(a  b  c)/2
角滑移面, n
(3) 金刚石滑移
= (a  b)/4，(b  c)/4，(a  c)/4 或(a  b  c)/4
金刚石滑移面 d, 
30
31
32
33
34
晶体中对称轴的图示符号
35
36
37
38
反映面和滑移面的图示符号
名称 符 图示符号 滑移量
号 ⊥投影面 ∥投影面 
反映面 m 
 
 a,b,c  t∥投影面 a/2, b/2 或 c/2 
轴滑移面
箭头指滑移方向 
a,b,c  t⊥投影面
对角滑 （ ±b）/2
移面 
n a
（b±c）/2 
（a±c）/2
箭头指滑移方向 （a±b±c）/2 * 
金刚石 d  
13 （a±b）/4 
滑移面  
箭头指法线方向为正
的方向
88
 
箭头指滑移方向
（b±c）/4 
（a±c）/4 
（a±b±c）/4 *
39
  
* 仅在四方晶系和立方晶系中存在该种滑移 
§4-2微观对称元素的组合
定理1 旋转轴与空间点阵组合 旋转轴 定平， 一
行于一阵点直线，并垂直于一阵点平面。
三斜 /
单斜 2//[010]，2⊥（010）
正交 2//[100]，[010]，[001]；2 ⊥(100)，(010)，(001)
四方 4//[001]; 4 ⊥(001)
2//[100],[010],[110];      2 ⊥(100),(010),(110)
三角 3//[001]; 3 ⊥(001)
2//[100] [010] 2 ⊥(2 10) (1 20), ;  - , -
六角 6//[001]; 6 ⊥(001)
2//[100] [010]; 2 ⊥(2-10) (1-20),   ,
立方 4//<100>; 4 ⊥{100}
3//<111>; 3 ⊥{111}
40
2//<100> or <110>; 2 ⊥{110} or {100}
定理2 反映面与空间点阵组合，反映面必定平行
于一阵点平面，其法线方向与一阵点直线相平行。
三斜 /
单斜 m//(010); n//[010]
正交 m//(100),(010),(001); n//[100],[010],[001]
四方 m//(100),(010),(100),(110),(1-10); 
n// [100],[010],[001],[110],[1-10]
三角 m//(210),(-1 20),(110);n//[100].[010],[110]
六角 m// (210) ( 1 20) (110) (001) , -  , ,
n// [100].[010],[110],[001]
立方
41
m//{100},{110}; n//<100>,<110>
定理3 n次旋转轴与垂直于它的格矢T组合，
将产生另一同轴次的旋转轴。它与原旋转轴平行
并位于t的中垂线上。
O'
αctgtd 
A' A"
22
ABB'
B"
O TD

42
t
2
t
t
43
t
3
3
t
3
3 1200
t
3
442400
6
450
t 6 3 6
t2
3
6
45
推论1 螺旋轴与垂直于它的格矢t组合，必导出
另一与其平行的同轴次螺旋轴，位于t的中垂线上。
O'
A' A"
B"

h= h=
ABB'
T

h=0
O D
2
αctg
2
td 
46
推论2 螺旋轴与任一格矢t组合，必导出另一与
其平行的同轴次的螺旋轴。新螺旋轴位于t的中垂
线上，它的平移分量为 +t||。t||和 t分别为格矢的平
行和垂直于原螺旋轴的分量。
t = t + t|| 
t t
t t
t|| = ½T 0
47
t||=0
48
49
6 61
3 36 66 6
2
11 1
t t21t||= 0
62
32
6
62
50t22
63 64
3 3
t63 2 t6
1 64
1 63
24
65
3 6
65
2
2
5
51t1
推论3 n次旋转轴与任一格矢t组合，若旋转操
作连续进行k次（kn/2时，n'=n/(n-k)。
推论4 n次螺旋轴与任一格矢t组合，若螺旋轴
连续操作k次（kn/2时 n'=n/(n k)
52
， - 。
   0  t||=
1/3 

 
53
 t 0 ||=
1/3 
 

54
3 + t =01  ||
1/3 

 
240
55
 t /3 ||=c
1/3 
 

56
 t /3 ||=c
1/3 

 
57
1/3
2/3 120
31 + t||=c/3
1/3
2/3
1
1/3
2/3 120
31 + t||=c/3
1/3
2/3
2/3
1/3
1/30
2
1/3
2/3
120
31 + t||=2c/3
2/3
1/3
3
1/3
2/3 120
31
2 + t||=2c/3
1/3
2/3
4
1/3
2/3
120
31 + t||=2c/3
1/3
2/3
240
5
1/3
2/3 120
32 + t||=c/3
1/3
2/3
240
6
1/3
2/3 120
32 + t||=2c/3
1/3
2/3
240
7
4 + t =0
8
41 + t =0
1/4
2/4
3/4
9
41 + t =c/2
1/4
2/4
3/4
3/4
2/4
1/4
10
42 + t =0
2/4
2/4
2/4
2/4
11
42 + t =c/2
2/4
2/4
2/42/4
12
43 + t =0
1/4
2/4
3/4 3/4
2/4
1/4
13
43 + t =c/2
1/4
2/4
3/4
3/4
2/4
1/4
14
1/3
2/3
61 + t||=0
2/3
1/6
1/2
5/6
1/6
60
15
1/3
2/3
61
2 + t||=0
2/3
1/6
1/2
5/6
1/3
120
16
1/3
2/3
61
3 + t||=0
2/3
1/6
1/2
5/6
1/3
1/2
17
1/3
2/3
61
4 + t||=0
2/3
1/6
1/2
5/6
1/3
1/2120
18
1/3
2/3
61
5 + t||=0
2/3
1/6
1/2
5/6
1/3
1/2
5/6
60
19
1/3
2/3
61 + t||=0
2/3
1/6
1/2
5/6
1/3
1/2
5/6
60
20
4/6
2/6
62 + t||=0
2/6
4/6
60
4/6
4/6
2/6
2/6
21
3/6
63 + t||=0
3/6
3/6
60
22
2/6
4/6
64 + t||=0
4/6
2/6
60
23
 
表 4-3  3 次轴与点阵平移矢量的组合 
 原对称轴 
ns
k 3 32 31 31
2 32 32
2 
kα 120° 240° 120° 240° 120° 240° 
kτ 0 0 c/3 2c/3 2c/3 4c/3 
新对称轴 
t||=0 3 3 31 31 32 32 
t||=c/3 31 32 32 3 3 31 
t||=2c/3 32 31 3 32 31 3 
注：k 为操作次数；α为原对称轴的基转角； 
τ为螺旋轴的平移分量； 
    t||为点阵平移矢量平行于螺旋轴的分量（下同）。 
24
4 次轴与点阵平移矢量的组合 
原对称轴 
ns
k 4 42 41 41
2 42 42
2 43 43
2 
kα 90° 180° 90° 180° 90° 180° 90° 180° 
kτ 0 0 c/4 c/2 c/2 c 3c/4 3c/2 
新对称轴 t||=0 4 2 41 21 42 2 43 21 
t||=c/2 42 21 43 2 4 21 41 2 
       注：原对称轴为 43、41
3、42
3、43
3 时，新对称轴分别与 4、41、42、43相同。 
25
 6 次轴与点阵平移矢量的组合 
ns
k 6 62 63 61 61
2 61
3 62 62
2 62
3 
kα 60 120 180 60 120 180 60 120 180 
原对称轴 
 kτ 0 0 0 c/6 c/3 c/2 c/3 2c/3 c 
新对称轴 t|| = 0 6 3 2 61 31 21 62 32 2 
 
ns
k 63 63
2 63
3 64 64
2 64
3 65 65
2 65
3 
α 60 120 180 60 120 180 60 120 180 
原对称轴 
 kτ c/2 c 3c/2 2c/3 4c/3 2c 5c/6 5c/3 5c/2 
新对称轴 t|| = 0 63 3 21 64 31 2 65 32 21 
   注：原对称轴为 6S
4、6S
5 时，新对称轴分别与 6S
2、6S
1 相同。 
26
定理4 反映面m和与其
垂直的格矢t组合，导出与原
反映面平行的另一反映面m'，
m与m'的间距为t/2。
m m'
a a
b b
t
A BC
推论1 两个相互平行的反
映面组合，导出与它们法线平
行的格矢，格矢的大小为两反
映面面间距的2倍。
m m'
t
t
t
推论2 反映面m与任一格矢t组合，导出一个
与反映面平行的滑移面m'，滑移面的平移分量τ =
t||，m与m'的间距d = t⊥/2。
27
定理5 对称中心i与平移矢
量t组合，导出另一反演中心i'，
i与i'之间相距t/2。
A B
A' B'
i
i'
C
t
t
定理6 2次螺旋轴与垂直于
它的滑移面组合，导出在 τ 1- τ 2
中点产生一反映中心i。
A
A'
B
C
τ2
τ1
21
28
 
金红石TiO2
O-2
Ti+4
§4-3 晶体微观对称性分析
29
0 0
0 0
0
0
0.5
0.5
0.5
u
u
u
u
u=0.3053 30
0 0
b1/4，3/4 1/4，3/4
1/4 3/4
0

n+a->n
，
 42+b 2+(a+ b)
0
-
P+2 ->2P
 1/4，3/4
0 0
a
93
0, 0.5
0 0
u
0

u

0u

u
0 0
94u=0.3053
金红石TiO2 四方晶系
95
b
1/4
/
 
  3 4
c
  0.25 
0.75


 
96
0 0
u
0

u

0u

u
0 0
97u=0.3053
a+b高度以（a+b）为单位
 c
          
0，0.5
          
98
0 0
b1/4，3/4 1/4，3/4
P 24 12 2
1/4 3/4
m n m
P 24
0
 ，
m
nm
 
0, 0.5
0, 0.5
0

0, 0.50, 0.5
 1/4，3/4
0 0
a
99
0, 0.5
0，0.5
正交:白铁矿FeS 2
a = 4.636 Å，b=5.414 Å， c=3.381 Å;  Z=2 
Fe （0 0 0) (0 5 0 5 0 5) , ,  . , . , .
S     (0.2,0.378,0)
(0.8,0.622,0)
(0.7,0.122,0.5)
(0.3,0.878,0.5)
100
101(001)
1c
1
4
1
4
4
5
2
.
A1
B1
.378
0 0
.378F1
a
.
.3
B2.878 E1
A2
122
.5
.7
.8 .622
.
.622E2
0 0
1
4
1
4
(010）
102
b
122 378 622 878 A1
1
4
. . . .
.2 .8B1
E1F1
0 0
11
c
A2 B2
44
.5.7 .3
2 8
E2 1
4
1
4
. . 00
（100）
103
1 1 1 1
1
4
0 0
0
A1
B1
F14 4
1 1
.122 .378 .622 .878
.2
4 4
.2
.5
A1
B1
.378
0 0
.378F1
0.5
0.5
0.5
A2E1 E2
4 4.3 .3
A2
B2.878
122
E1
.5
0 0
0B2
1
4
1
4
.7
.8
1
.7
.8 .622
.
.622E2
0 0
F2 1
4 4
.122 .378 .622 .878 A1
1
4
.2 .8
A2
B1
B2
E1F1
0 0
1
4
1
4
P
222 11
.5.7 .3
.2 .8
E2
00
1
4
1
4 mnn
104
对称元素的分布规律：
(1) 同一方向上，同种对称元素相互平行，排列
规律 同晶体点阵；
(2) 同一方向上，可以平行排列着不同种类、不
同轴次的对称元素;
(3) 对称元素将晶体中等质点联系起来；
(4) 微观对称元素与宏观对称元素方向上完全一
致，
宏观 微观
对称轴 对称轴 螺旋轴 可衍生低轴次对称轴， ， ；
反映面 反映面，滑移面。
105
§4 4空间群的推导-
晶 体
宏观
对称性
点 群
平移轴，附加阵点
微观对
空 间 群
称性
106
1、从点群4（C4）导出它包括的空间群
4 → 4，41，42，43
四方晶系
布喇菲点阵
I4P4
I41
I4
P41
P4
2
I43
2
P43
107
P(简四方)+4 （4, 41, 42, 43) 平移矢量（a或b)
A
BC
E
P4 P41 P42 P43
108
I+4
A
D
C B
I4 I41 I42=I4 I43=I41
109
简四方P( )
+4 （4 4 4 4 ), 1, 2, 3
I(体心四方)
P4 P41 P42 P43, , , 
I4, I41
110
2、从4/m点群导出它包括的空间群
4 + m⊥→ 4/m
4 +(a, n, d)⊥ → (P4，P41，P42，P43，I4，I41 )
+ (a n d)⊥ , , 
P4/m，P4/n，P42/m，P42/n，
I4/m (I4/n)和I41/a  (I41/b) 
111
P4:m ,n,  a, b, d      P41: m,a,b,n,d P42:m, n, a,b,d
112
P43:m,a,b,n,d I4:m (n),  a,b,d I41: a (b), m,n,d
从点群导出空间群：
(1) 从点群所属的晶系确定可能存在的空间点阵
类型 并与相应的宏观对称元素组合， ；
(2) 从点群国际符号确定其特征方向上的对称元
素，用对称元素组合定理导出全部对称元素；
(3) 用微观对称中可能出现的螺旋轴 滑移面等、
分别代替点群中对应的宏观对称元素，与可能的平
移群组合 导出可能出现的对称元素 所有可能出； ，
现的微观对称元素组合类型；
(4) 除出不合理的组合及等效的组合类型，从而
得到独立的空间群。
113
§4-5 230种空间群 
1、空间群的表示符号
各晶系的特征方向
点阵 第一特 第二特 第三特
类型 征方向 征方向 征方向
 
晶系 第一特征方向 第二特征方向 第三特征方向 注 
三斜 [100]
P、F、I、
C R
空间群 F
d
14
3
_
2
m  
 
单斜 [010]    
正交 [100] [010] [001]  
四方 [001] [100] [110]、  
点群 4
m 3
_ 2
m  
 
三角 [111]        菱面体坐标系 
[001] [100] [210] 六角坐标系
[110]
空间群的熊夫利符号：点群的熊夫利符号的右上
角增加一个编号
六角 [001] [100] [210]  
立方 [001] [111] [110]  
例：C4: C4
1，C4
2，C4
3，C4
4，C4
5，C4
6
114P4，P41，P42，P43，I4，I41 (国际符号)
115
对称元素分布图 一般等效点系图
116
117
118
119
120
121
122
123
124http://img.chem.ucl.ac.uk/sgp/large/sgp.htm
2、空间群
230种空间群
对映空间群 种：11
对称元素及其分布
相同、仅螺旋轴的手性
不同的两个空间群 石英：P3121           P3221
三角晶系 P31 (P32)、P3112 (P3212)、P3221 (P3121)
四方晶系 P4 (P4 ) P4 22 (P4 22) P4 2 2 (P4 2 2)1 3 、 1  3 、 1 1  3 1
六角晶系 P61 (P65)、P62 (P64)、P6122 (P6522)、P6222 (P6422)
125立方晶系 P4332（P4132）
晶体的230种空间群晶体的230种空间群
三斜
空  间  群 
国 际 符 号
点 
序 熊夫利 
群 
号 完 全 简 约 符 号
1-C1 1  P1 
C1
1  
1
_
-Ci 2 
 
P1
_ Ci
1  
 
126
单斜
2-C2 3 P121 P2 
C2
1  
 4 P1211 P21 C2
2  
 5 C121 C2 
C2
3  
C 6 P1 1 Pm- s m m 
Cs
1  
7 P1c1 Pc 
C2
s
 8 C1m1 Cm 
C3
s
 9 C1c1 Cc 
Cs
4  
127 
10
P1 2 1
P2/m 
C12
m  h2m
C2h 11 21
P21/m C2P1 m 1 h2
12 C2/m
C1 2
m 1 C h2
3
13 P2/
P1 2
c 1 
c
C h2
4
14
P1 21
c 1 
P21/c C h2
5
 15
C1 2
c 1 
C2/c 
C h2
6
128 
222 16 P222 P222 
D2
1  
正交
D2(V) 17 P2221 P2221 D2
2
18 P21212 P21212 D2
3
19 P212121 P212121 D2
4
 20 C2221 C2221 D5
2
 21 C222 C222 
D2
6
 22 F222 F222 
D2
7
 23 I222 I222 
D2
8
129
 24 I212121 I212121 D2
9
mm2 25 Pmm2 Pmm2 
C2
1
v
C2v 26 Pmc21 Pmc21 2 
C v2
27 Pcc2 Pcc2
C v2
3
 28 Pma2 Pma2 
C4
v2
130
mm2 29 Pca21 Pca21 C2
5
v
C2v 30 Pnc2 Pnc2 
C v2
6
 31 Pmn21 Pmn21 C v2
7  
 32 Pba2 Pba2 
C v2
8  
 33 Pna21 Pna21 C v2
9  
 34 Pnn2 Pnn2 
C v2
10  
 35 Cmm2 Cmm2 
C v2
11  
131
 
36 Cmc21 Cmc21 C v2
12  
37 Ccc2 Ccc2 13 
C v2  
 38 Amm2 Amm2 
C v2
14
 39 Abm2 Abm2 
C v2
15
 40 Ama2 Ama2 
C v2
16
41 Aba2 Aba2 17C v2
 42 Fmm2 Fmm2 
C v2
18
 43 Fdd2 Fdd2 
C v2
19
44 Imm2 Imm2 
C v2
20
45 Iba2 Iba2 
C21
132
v2
 46 Ima2 Ima2 
C v2
22
2
m
2
m
2
m
47
P 2
m
2
m
2
m
Pmmm
D h2
1
(mmm) 48
P 2
n
2
n
2
n
Pnnn 
D h2
2
D2h(Vh) 49 2 Pccm 3P 2
c
2
c m D h2
 50
P 2
b
2 2 Pban 
D h2
4
a n
 51
P 21
m
2
m
2
a
Pmma
D h2
5
 52
P 2
n
21
n
2
a
Pnna 
D h2
6
53 P
P 2
m
2
n
21
a
mna
D h2
7
 54
P 21 2 2 Pcca 
D8
c c a h2
 55
P 21
b
21
a
2
m
Pbam
D h2
9
133 56
P 21
c
21
c
2
n
Pccn 
D h2
10
57 P 2
b
21
c
21
m  Pbcm D h2
11
21 21 2 D12
61 P 21
b
21
c
21
a Pbca D h2
15
62 P 21 21 21 Pnma D16
58 P n n m  Pnnm h2
59 P 21
m
21
m
2
n  Pmmn D h2
13
n m a h2
63 C 2
m
2
c
21
m Cmcm D h2
17
64 C 2 2 21 C D18
60 P 21
b
2
c
21
n  Pbcn D h2
14
 
m c a mca h2
65 C 2
m
2
m
2
m Cmmm D h2
19
2 2 2 2066 C c c m Cccm D h2
67 C 2
m
2
m
2
a Cmma D h2
21
68 C 2
c
2
c
2
a Ccca D h2
22
69 F 2
m
2
m
2
m Fmmm D h2
23
70 F 2
d
2
d
2
d Fddd D h2
24
71 I 2
m
2
m
2
m Immm D h2
25
72 I 2
b
2
a
2
m Ibam D h2
26
73 I 21 21 21 Ibca D27
134
b c a h2
74 I m
21
m
21
a
21 Imma D h2
28
四方
4 75 P4 P4 C4
1
C4 76 P41 P41 C4
2  
3 77 P42 P42 C4
78 P43 P43 C4
4 
 79 I4 I4 C4
5  
 80 I41 I41 C4
6  
135
4
_
-S4 81 P 4
_
P 4
_
S4
1 
 82 I 4
_
 I 4
_
 S4
2  
4
m  83 P4/m P4/m C h4
1
C 84 P4 / P4 / C2
4h 2 m 2 m h4
 85 P4/n P4/n C h4
3
 
86 P42/n P42/n C4  h4
87 I4/m I4/m C h4
5
88 I41/a I41/a C h4
6
 
136
422 89 P422 P422 D4
1
D4 90 P4212 P4212 D4
2
3 91 P4122 P4122 D4
 92 P41212 P41212 D4
4
 93 P4222 P4222 D4
5  
94 P4 2 2 P4 2 2 D6  2 1  2 1 4
 95 P4322 P4322 D4
7
 96 P43212 P43212 D4
8
97 I422 I422 D9 4
 98 I4122 I4122 D4
10
137
 
4mm 99 P4mm P4mm C v4
1
C4v 100 P4bm P4bm C v4
2
101 P4 cm P4 cm C3 2 2 v4
 102 P42nm P42nm C v4
4
5 103 P4cc P4cc C v4
 104 P4nc P4nc C v4
6
 105 P42mc P42mc C v4
7
106 P42bc P42bc C4
8 v
 107 I4mm I4mm C v4
9
C10 108 I4cm I4cm v4
 109 I41md I41md C v4
11
138
 110 I41cd I41cd C v4
12
4
_
2m 111 P 4
_
2m P 4
_
2m D d2
1
2D2d 112 P 4
_
2c P 4
_
2c D d2
 113 P 4
_
21m P 4
_
21m D d2
3
 114 P 4
_
21c P 4
_
21c D d2
4
115 P 4
_
m2 P 4
_
m2 D d2
5
116 P 4
_
c2 P 4
_
c2 D d2
6
117 P 4
_
b2 P 4
_
b2 D d2
7
118 P 4
_
n2 P 4
_
n2 D d2
8
119 I 4
_
m2 I 4
_
m2 D d2
9
120 I 4
_
2 I 4
_
2 D10c c d2
121 I 4
_
2m I 4
_
2m D d2
11
12
139
122 I 4
_
2d I 4
_
2d D d2
4
m
2
m
2
m  123 P 4
m
2
m
2
m P4/mmm D h4
1
( 4
m mm) 124 P 4
m
2
c
2
c P4/mcc D h4
2
D 125 P 4 2 2 P4/nbm D3
4h n b m h4
 126 P 4
n
2
n
2
c P4/nnc D h4
4
 127 P 4
m
21
b
2
m P4/mbm D h4
5
 128 P 4
m
21
n
2
c P4/mnc D h4
6
 129 P 4
n
21
m
2
m P4/nmm D h4
7
130 P 4 2 2 P4/ D8 n c c ncc h4
 131 P m
42 2
m
2
c P42/mmc D h4
9
 132 P m
42 2
c
2
m P42/mcm D h4
10
 
140
133 P n
42 2
b
2
c P42/nbc D h4
11
134 P n
42 2
n
2
m P42/nnm D h4
12
135 P 42 21 2 P4 /mbc D13
m b c 2 h4
136 P m
42
n
21 2
m P42/mnm D h4
14
137 P n
42 21
m
2
c P42/nmc D h4
15
138 P 42 21 2 P4 / D16
n c m 2 ncm h4
139 I 4
m
2
m
2
m I4/mmm D h4
17
140 I 4
m
2
c
2
m I4/mcm D h4
18
4 2 2 19141 I 1
a m d I41/amd D h4
142 I 41 2 2
d I41/acd D h4
20
141
a c
 
三角 3-C3 143  P3 C3
1  
 144 P31 P31 C3
2  
145 P32 P32 C3
3
146 R3 R3 C3
4  
3
_
C 147 P 3
_
P 3
_
C1- 3i  i3
 148 R 3
_
 R 3
_
 C i3
2
32 149 P312 P312 D1  3
D3 150 P321 P321 D3
2
3 151 P3112 P3112 D3
 152 P3121 P3121 D3
4
 153 P3212 P3212 D3
5  
 154 P3221 P3221 D3
6
142 155 R32 R32 D3
7
3m 156 P3m1 P3m1 C v3
1
2D3v 157 P31m P31m C v3
 158 P3c1 P3c1 C v3
3
 159 P31c P31c C v3
4
160 R3m R3m C3
5 v
 161 R3c R3c C v3
6
162 P31 2 P 3
_
1 D13
_
2
m m d3
163 P 3
_
1 2
c P 3
_
1c D d3
2
m  
( 3
_
m) 
2 3164 P 3
_
m 1 P 3
_
m1 D d3
D3d 165 P 3
_
2
c 1 P 3
_
c1 D d3
4
 166 R 3
_
2
m  R 3
_
m D d3
5
167 R 3
_
2 R 3
_
c D d3
6
143
 c
 
6 168 P6 P6 C6
1  
2
六角
C6 169 P61 P61 C6  
170 P65 P65 C6
3
 171 P62 P62 C6
4  
 172 P64 P64 C6
5  
 
 173 P63 P63 C6
6  
_ _ _ 16 -C3h 174 P 6 P 6 C h3
6 -C6h 175 P6/m P6/m C h6
1
m
 176 P63/m P63/m C h6
2
144
622 177 P622 P622 D6
1  
D6 178 P6122 P6122 D6
2  
179 P6 22 P6 22 D3 5 5 6
 180 P6222 P6222 D6
4  
 181 P6422 P6422 D6
5  
182 P6 22 P6 22 D6 3 3 6
6mm 183 P6mm P6mm C v6
1
C6v 184 P6cc P6cc C v6
2
185 P6 P6 C3 3cm cm v6
 186 P63mc P6mc C v6
4
145 
6
_
m2 187 P 6
_
m2 P 6
_
m2 D h3
1 
D3h 188 P 6
_
c2 P 6
_
c2 D h3
2
 189 P 6
_
2m P 6
_
2m D h3
3
190 P 6
_
2 P 6
_
2 D4 c c h3
6
m
2
m
2
m  191 P 6
m
2
m
2
m P6/mmm D h6
1
( 6
m mm) 192 P 6
m
2
c
2
c P6/mcc D h6
2
D6h 193 P 63
m
2
c
2
m P63/mcm D h6
3
194 P 63 2 2 P6 /mmc D4 m m c 3 h6
 
146
立方 23 195 P23 P23 T1  
T 196 F23 F23 T 2  
 197 I23 I23 T 3
 198 P213 P213 T 4  
199 I213 I213 T 5  
2
m 3
_
200 P 2
m 3
_
Pm 3
_
 Th
1  
2 _ _
T 2Th 201 P n 3 Pn 3 h
 202 F 2
m 3
_
 Fm 3
_
 Th
3  
203 F 2
d 3
_
 Fd 3
_
 Th
4  
204 I 2
m 3
_
 Im 3
_
 Th
5  
205 P 21
a 3
_
 Pa 3
_
 Th
6  
206 I 21
a 3
_
Ia 3
_
Th
7
147
432 207 P432 P432 O1  
O 208 P4 32 P4 32 O2 2 2  
 209 F432 F432 O3  
 210 F4132 F4132 O4  
211 I432 I432 O5 
 212 P4332 P4332 O6  
7 213 P4132 P4132 O  
214 I4132 I4132 O8
 
148
4
_
3m 215 P 4
_
3m P 4
_
3m Td
1  
_ _
T 2Td 216 F 4 3m F 4 3m d
217 I 4
_
3m I 4
_
3m Td
3 
 218 P 4
_
3n P 4
_
3n Td
4  
 219 F 4
_
3c F 4
_
3c Td
5  
220 I 4
_
3d I 4
_
3d T 6 d
 
149
4 3
_ 2 221 4 3
_ 2 3
_
O1
m m P m m Pm m h
(m 3
_
m) 222 P 4
n 3
_
2
n Pn 3
_
n Oh
2  
Oh 223 P m
42 3
_
2
n Pm 3
_
n Oh
3  
 224 P n
42 3
_
2
m Pn 3
_
m Oh
4
 225 F 4
m 3
_ 2
m Fm 3
_
m Oh
5  
226 F 4 3
_
2 F 3
_
O 6 m c m c h
 227 F 41
d 3
_ 2
m Fd 3
_
m Oh
7  
4 2 8 228 F 1
d 3
_
c Fd 3
_
c Oh  
 229 I 4
m 3
_ 2
m Im 3
_
m Oh
9  
 230 I 41
a 3
_
2
d Ia 3
_
d Oh
10
150
 
晶体在各空间群的分布
斜 单斜 交 四方 角 六角 立方三 正 三
3.2% 16.4% 17.2% 10.5% 7.7% 6.2% 38.8%
46 2%的晶体分布在22个空间群
晶体最多的7个空间群
.
2 2 2
11, B2/m, P2 /b, B2/b, P , Fm3m, Fd3m
n m a
151
下列空间群所属的晶系、布拉菲点阵类型、点群、特征方
向 宏观对称操作元素及数目 特征方向上的微观对称操
P6 22
、 、
作元素。
Ia3d 1
m3m 622
3L44L36L29PC L66L2
F43c P42nm
43m 4mm
3Li
44L36L2 L44P
Pa3 Fddd
3 mmm
151
m
3L24L33PC 3L23PC
晶体在各空间群的分布
斜 单斜 交 四方 角 六角 立方三 正 三
3.2% 16.4% 17.2% 10.5% 7.7% 6.2% 38.8%
46 2%的晶体分布在22个空间群
晶体最多的7个空间群
.
2 2 2
11, B2/m, P2 /b, B2/b, P , Fm3m, Fd3m
n m a
C C
152
§4-6 等效点系
1 基本概念、
等质点: 化学性质相同的点。
等同点: 化学性质相同 近邻原子的配置也相同的点， 。
153
等效点: 从一点出发 经全部对称元素的作用后 得到一， ，
系列规则分布的点。
等效点系: 经对称元素作用后所得到的等效点的总和。
特殊等效点系, 一般等效点系
等效位置: 等效点占据的位置 威科夫（Wykoff）位置,
等效点的重复数: 一个惯用晶胞的等效点数目
154
2、威科夫位置
空间群 P 2 的等效点系
Pmm2:（001）
mm
威科夫位置 位置的对称性 等效点的坐标 
4i 1 xyz, 
_
x yz, 
_
x
_
y z, x
_
y z
a
be
i
2h m x 2
1 z, 
_
x 2
1  z 
2g m x0z, 
_
x 0z c
g
d
h
f2f m 2
1 yz, 2
1
_
y z 
2e m 0 y z, 0
_
y z 
1 1
1d mm2 2 2 z
1c mm2 2
1 0z 
1b mm2 0 2
1 z 
1a mm2 00z 
155
No 225 Space Group: F 4/m -3 2/m.       
General position 192 l Site symmetry: 1         
Wyckoff position 96k    Site symmetry: ..m
Wyckoff position 96j    Site symmetry: m..
k ff i i 48i Si 2Wyc o  pos t on     te symmetry: m.m  
Wyckoff position 48h Site symmetry: m.m2        
Wyckoff position 48g    Site symmetry: 2.mm
Wyckoff position 32f    Site symmetry: .3m
156
Wyckoff position 24e    Site symmetry: 4m.m
Wyckoff position 24d Site symmetry: m.mm        
Wyckoff position 8c    Site symmetry: -43m 
Wyckoff position 4b    Site symmetry: m-3m
Wyckoff position 4a Site symmetry: m 3m
1/2,1/2,1/2              1/2,0,0                  0,1/2,0                  0,0,1/2 
        -
0,0,0                    0,1/2,1/2                1/2,0,1/2                1/2,1/2,0 
157
 P3 空间群的威科夫位置资料 
NO 143 P3.  
威科夫符号，位置对称性 威科夫位置 
3 d 1 x,y,z -y,x-y,z -x+y,-x,z  
1 c 3.. 2/3,1/3,z      
1 b 3.. 1/3,2/3,z      
1 3 0 0 a .. , ,z  
       
                     
空间群的威科夫位置资料 
No.146 R3 
威科夫符号位置对称性 威科夫位置
9 b 1 x,y,z -y,x-y,z -x+y,-x,z 
   x+2/3,y+1/3,z+1/3 -y+2/3,x-y+1/3,z+1/3 -x+y+2/3,-x+1/3,z
  x+1/3,y+2/3,z+2/3 -y+1/3,x-y+2/3,z+2/3 -x+y+1/3,-x+2/3,z
3 a 3. 0,0,z 2/3,1/3,z+1/3 1/3,2/3,z+2/3 
158
 
例:尖晶石型结构MgAl2O4 AB2X4， , Z=8 F
md
2341
威科夫符号位置对称性 (0,0,0)+     (0, 2
1 , 2
1 )+     ( 2
1 ,0, 2
1 )+     ( 2
1 , 2
1 ,0)+ 
192 i 1 x,y,z x y + 1 z+ 1 x + 1 y+ 1 z x+ 1 y z + 1, 2 , 2  2 , 2 , 2 , , 2  
   z,x,y z+ 2
1 , x , y + 2
1  z , x + 2
1 ,y+ 2
1  z + 2
1 , x+ 2
1 , y  
   y,z, x y + 2
1 ,z+ 2
1 , x  y+ 2
1 , z , x + 2
1  y , z + 2
1 , x+ 2
1  
  ……
96 h ..2 
8
1 ,y, 
y + 4
1
8
7 , y + 2
1 , y + 4
3
8
3 , y+ 2
1 , y+ 4
3  
8
5 , y ,y+ 4
1  
1 3 7 1 y+ 3 3 y+ 1 1 5  y + 4 ,
8
1 y
y + 4 , 8 , y + 2 4 , 8 , 2 y+ 4 , 8 , y
   ……    
96 g ..m x,x,z x , x + 2
1 , z+ 2
1  x + 2
1 , x+ 2
1 , z  x+ 2
1 , x , z + 2
1  
   z,x,x z+ 2
1 , x , x + 2
1  z , x + 2
1 , x+ 2
1 z + 2
1 , x+ 2
1 , x  
159   ……    
96 g ..m x,x,z x , x + 2
1 , z+ 2
1  x + 2
1 , x+ 2
1 , z  x+ 2
1 , x , z + 2
1  
z x x + 1 + 1 + 1 + 1 + 1 + 1  , , z 2 , x , x 2  z , x 2 , x 2 z 2 , x 2 , x  
   ……    
48 f 2 0 0 0 0 .mm x, , x , 2
1 , 2
1  ,x,
2
1 , x , 2
1  
   0,0,x 
2
1 , 2
1 , x  4
3 , x+ 4
1 , 4
3  
4
1 , x + 4
1 , 4
1  
  x+ 4
3 , 4
1 , 4
3 _
x + 4
3 , 4
3 , 4
1  4
3 , 4
1 ,
_
x + 4
3  4
1 , 4
3 , x+ 4
1
32 e .3m x, x, x _
x ,
_
x + 2
1 , x+ 2
1  
_
x + 2
1 , x+ 2
1 , x x+ 2
1 ,
_
x ,
_
x + 2
1  
   x+ 4
3 , x+ 4
1 , 
_
x + 3
_
x + 4
1 ,
_
x + 4
1 , 
_
1
x+ 4
1 ,
_
x + 4
3 , 
x+ 3
_
x + 4
3 , x+ 4
3 ,  
x+ 1
4 x + 4
4 4
16 d
. 3
_
m 8
5 , 8
5 , 8
5  8
3 , , 8
1  , 8
1 , 8
3  8
1 , 8
3 , 8
7 
16 c
. 3
_
m 8
1 , 8
1 , 8
1
8
7 , 8
3 , 8
5
8
3 , 8
5 , 8
7
8
5 , 8
7 , 8
3
8 b 4 3m 2
1 , 2
1 , 2
1  4
1 , 4
3 , 4
1    
160
8 a 4 3m 0,0,0
4
3 , 4
1 , 4
3  
8 A离子:8(a)位置; 16 B离子:16(d)位置; 32阴离子X:32(e)位置: 参数x3/8。
尖晶石: Mg2+占8a位置，Al3+:16d，O2-:32e位置
Mg2+
Al3+
O2-
161