概要信息：

第三章
晶体的宏观对称性
5
5
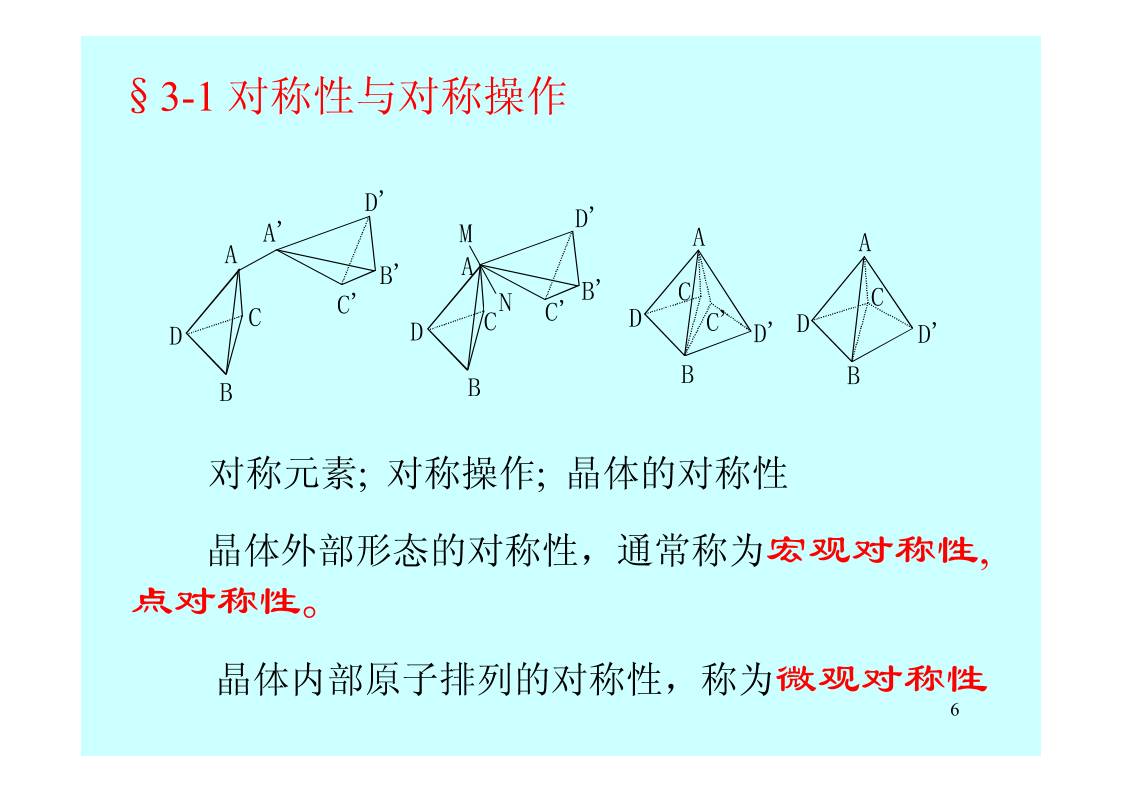
§3-1 对称性与对称操作
D'
D'
A
A'
B'
C'
A
M
N B'
C'
A
C
A
C
B
C
D
B
D C
B
D
D'C'
B
D D'
对称元素;  对称操作;  晶体的对称性
晶体外部形态的对称性，通常称为宏观对称性,  
点对称性。
晶体内部原子排列的对称性 称为微观对称性
6
，
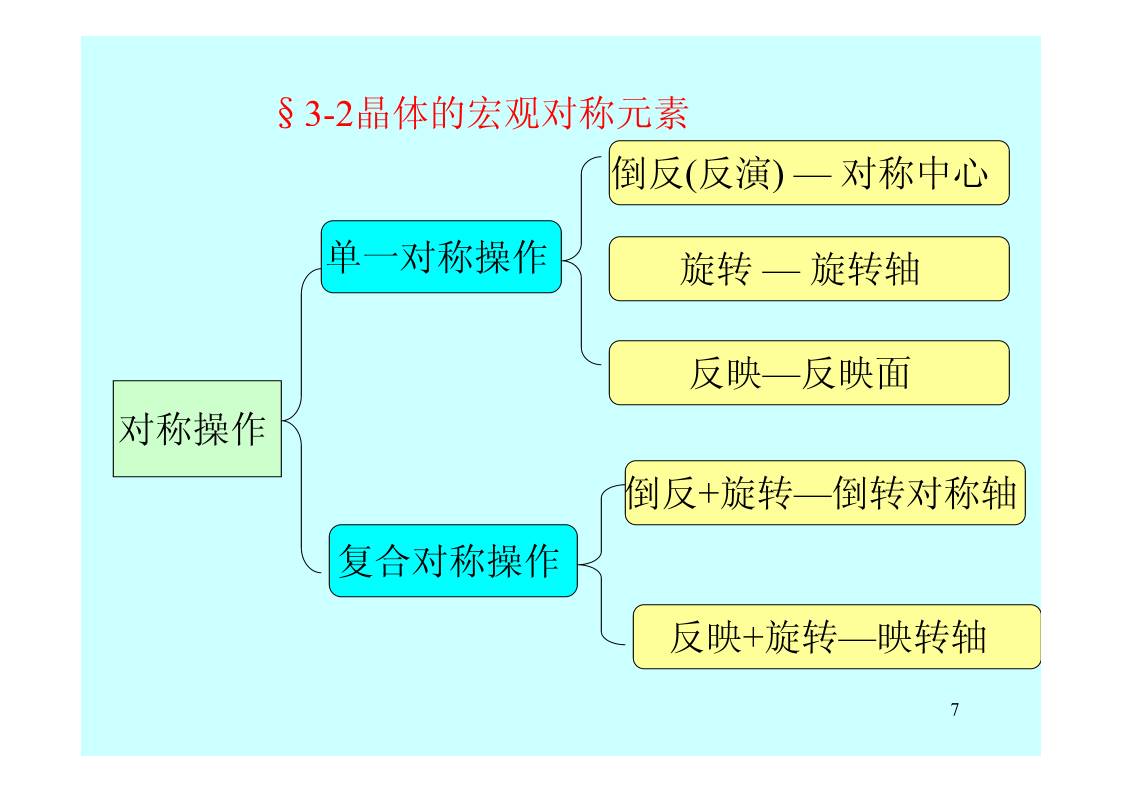
§3-2晶体的宏观对称元素
倒反(反演) — 对称中心
单一对称操作 旋转 — 旋转轴
反映—反映面
对称操作
倒反+旋转 倒转对称轴
复合对称操作
—
反映+旋转—映转轴
7
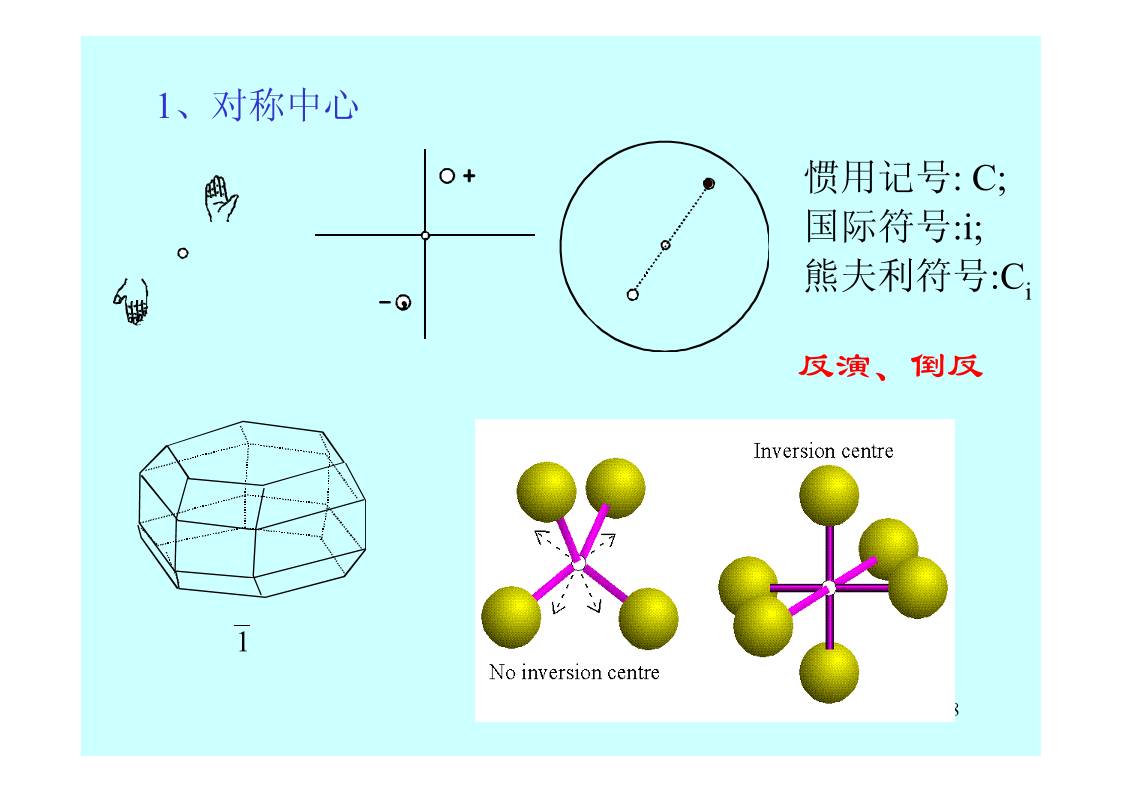
1、对称中心
惯用记号: C;
国际符号 i: ;
熊夫利符号:Ci
反演、倒反
1
8
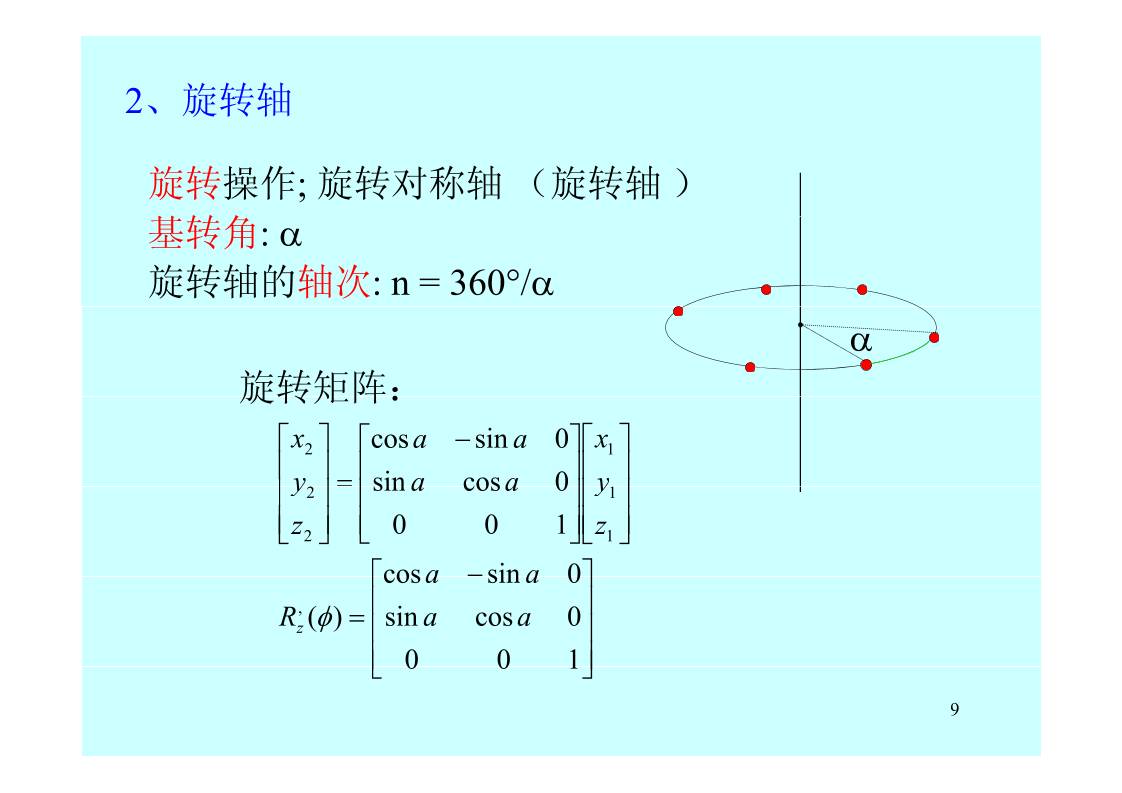
2、旋转轴
旋转操作; 旋转对称轴（旋转轴）
基转角: 
旋转轴的轴次: n = 360/

旋转矩阵：











 






0cossin
0sincos
1
1
2
2
y
x
aa
aa
y
x
 

0sincos
100 12
aa
zz








100
0cossin)(, aaRz 
9
AB AC AD
N只能是1，2，3，4，6 没有5或者7等更高次
       , 
AD = AC = AB
AE = m·AB    AE = 2·AC·cos
m = |2·cos| (m整数，晶体的平移周期性）
-2 ≤ m ≤ 2
2 1 0 1 2m：- 、- 、 、 、 ，
：180，120，90，60和360
n =1、2、3、4、6
1 2 3 4 6常用符号 L n：L 、L 、L 、L 、L
Hermann-Mauguin(国际)符号：1、2、3、4、6
10
熊夫利符号：C1、C2、C3、C4、C6
+
1 1          
+
+
2(C ) 2
11
2
12
+
+
+
3
3(C3)
+
+
+
+
4(C4)
13
4
+
+
+
+
+ +
6(C6) 6
一个晶体中可以不存在旋转轴，也可
有 种旋转轴 时存在以 几 同 。
不同晶体有着不同的旋转轴组合方式。
14
3。反映面（对称面、镜面）
m m
常用 国际 熊夫利：P     ：m      ：Cs
个晶体中可以没有反映面 也可以有一 ，
一个或有限的几个反映面，反映面之间的夹
15
角只能取某些特定的值。
4。倒转轴
旋转一定角度后，再进行倒反：1,  2,  3,  4,  6
A
C +
A'
1
-
, +-
1
2
m
23
162 m
3
12
B C
A ,+
-,
+
-
,+
-
3
3 3 1 
173
+
,, -
-
+
4
184
+,-
+- ,
+- ,
6
6 3 m 
19
L 1 L 2 L 3 L 4 L 6
2 3 4 61
i , i , i , i , i
, , ,,
C 1i, C 2i, C 3i, C 4i,C 6i
Li
1 = C
Li
2 = P
L 3 C3
i
3 =  +  
Li
4
L
Li
6 = 3 + PL3
20
晶体中可以没有倒转轴，也可以有一个
或有 的 个特定的倒转轴 倒转轴 须交限 几 ， 必
于一点。
5. 映转轴
映转操作 旋转 反映= 后再
1次映转轴 Ls
1 2次映转轴 LS
2 3次映转轴 LS
3
t
t
t
t
t
t
21
4次映转轴 LS
4 6次映转轴LS
6 
12
3 4
m
t
1' 4' t
2' 3'
Ls
1 = P = Li
2 LS
2 = C = Li
1
LS
3 = L3 +P = Li
6 LS
4 = Li
4
6 3 3
22
LS = L +C = Li
点对称操作 对称元素、
L1、L2、L3、L4、L6、C、P和Li
4。
其它的对称元素可以由这8个对称元素中的两个
对称元素组合而成。
其中，Li
6 =  L3+P，但Li
6的轴次高于L3，Li
6属于
六角晶系中的对称元素，习惯上不用L3+P来代替。
轴次为3 4 6的旋转轴 倒转轴等对称轴叫做、 、 、
高次轴。
23
§3-3 对称元素组合定理
1. 欧拉定理
任意两个旋转轴相交 定产生通过交点的另，一 一
旋转轴，它的作用等于前两个旋转轴操作之积。
B

D F
 



C




24
2、旋转轴的组合
旋转轴 轴之间的夹角
次    说    明 
A B C B、C 轴 A、C 轴 A、B 轴
2 2 2 90° 90° 90° 可能的组合 
3 90° 90° 60° 可能的组合
4 90° 90° 45° 合可能的组 
6 90° 90° 30° 可能的组合
3 3 70.529° 54.736° 54.736° 可能的组合 
4 54.736 45° 35 264° 可能的组合
° 
.
6 0° 0° 0° 无意义 
4 4 0° 0° 0° 无意义 
6 / / / 不可能的组合
25
  
6 6 / / / 不可能的组合 
 
3 3 3 0° 0° 0° 无意义
4 / / / 不可能的组合
不 能的组合6 / / / 可
4 4 / / / 不可能的组合
6 / / / 不可能的组合
6 6 / / / 不可能的组合
4 4 4 / / / 不可能的组合
4 6 / / / 不可能的组合
6 6 / / / 不可能的组合
6 6 6 / / / 不可能的组合
26
旋转轴的可能组合
⑴两个2次轴以30°、45°、60°或90°相交；
⑵ 2次轴与3次轴以54.736°、35.264°或90°相交；
⑶ 2次轴与4次轴以45° 90°相交；、
⑷ 2次轴与6次轴以90°相交；
⑸两个3次轴以70.529°相交；
⑹ 3次轴与4次轴以54.736°相交。
除了上述组合外 其他组合都不可能从欧拉定理，
组合而得到
27
旋转轴组合定理
定理1 一个n次轴与一个垂直于它的2次轴相交，则必
有n个2次轴垂直于此n次轴。
A2B2
A3 B3
A1B1
推论 如果两个2次轴的夹角为90。、60°、45°或
30°时，必有一个2、3、4或6次轴垂直于这两个2次轴。
28
定理2 一个n次旋转轴与另一个m次旋转轴相交，其
夹角为δ时 则n次轴周围必有n个呈对称分布的m次，
轴，m次轴周围必有m个呈对称分布的n次轴。这些
轴相交于一点 任何两相邻的n次轴 m次轴间的夹， 、
角为δ。
2
29m 3  (3L24L33PC) 432  (3L44L36L2)
旋转轴相交时 旋转轴轴的轴次和夹角，
必须满足旋转轴组合定律:
n                          m
2                   2、3、4、6
3 2 3 4                   、 、
4 2、3、4                   
6                   2
30
旋转轴间的夹角
（1）两个2次轴以30° 45° 60°或90°相交、 、 ；
（2）2次轴与3次轴以54.736°、35.264°或90°相交；
（3）2次轴与4次轴以45°、90°相交；
（4）2次轴与6次轴以90°相交；
（5）两个3次轴以70 529°相交. ；
（6）3次轴与4次轴以54.736°相交；
（7） 4次轴与4次轴以90°相交。
31
3、反映面的组合
定理3 两个反映面相交，交角为α时，则交线是一
个基转角为2的旋转轴。
L
晶体中只有 1、2、3、4
和6次轴→反映面之间夹角只

C
能是180、90、60、45和30°
存在 个以上对称面的晶
B
MN
2
体中必然存在对称轴
推理1 当n个反映面等角度相交于同一直线时，此直
线必定是n次旋转轴。
推理2 如果一个反映面包含一个n次旋转轴，则必有
32n个反映面包含此n次旋转轴。
4 旋转轴与反映面的组合、
定理4 偶次旋转轴与垂直于它的反映面组合，偶次
轴与反映面的交点必定是对称中心。
A3A4 A3
A B
t
A1
A2
A1 A2
t
m
i
P P
C
B1 B2
B3
B4
B1 B2
B3
33
定理5 反映面上若存在对称中心 则存在通过对
5、对称中心与旋转轴、反映面的组合
，
称中心并垂直于该反映面的2次轴。
A D
m mc
B C
定理6偶次轴上若有对称中心，则存在通过对
称中心并与该偶次轴垂直的反映面
定理7晶体中有对称中心时，偶次轴的总数必定
等于反映面的总数
34
。
6。倒转轴的组合
定理8 如果反映面包含Li
n，或Li
n垂直于L2:
为奇 个2次轴⊥ L n 个反映面∥L nn ，n i ，n i ；
n为偶，n/2个2次轴⊥ Li
n，n/2个反映面∥Li
n；
反映面的法线与相邻2次旋转轴之间的夹角均为360 /2 n。
Li
1 = C
C + P PL2 C   → ⊥
C+L2 →PL2
⊥C
35
下列组合正确的是:
L43P L22P 3L2
L3PC L6PC 3L 3P
36
2
m 3  (3L24L33PC) 432  (3L44L36L2)
37
6、倒转轴的组合
定理8 如果反映面包含Li
n，或Li
n垂直于L2:
为奇 个2次轴⊥ L n 个反映面∥L nn ，n i ，n i ；
n为偶，n/2个2次轴⊥ Li
n，n/2个反映面∥Li
n；
反映面的法线与相邻2次旋转轴之间的夹角均为360 /2 n。
Li
1 = C
C + P →PL2
⊥C
C L2 PL2 C+  → ⊥
38
Li
3+ P∥
39
Li
3+ 2⊥
40
定理9 如果一个2次轴与反映面斜交，2次轴与反
映面法线的交角为δ，则必有一个n次倒转轴平行于反
映面并与2次旋转轴垂直，n=360/2δ。
P+260
 
41
= 90 、60 、45 、30
晶体中满足群的性质定义的点对称操作的集合称
作晶体学点群 点对称操作的共同特征市进行操作。
后物体中至少与一点保持不动。
晶体学中点对称操作只有：1，2，3，4，6及其
反轴和对称中心以及反映面。
将这些对称操作元素按所与可能的方式组合起来，
就得到32个晶体学点群。
43
1 旋转群、 ：
单一旋转轴: 5种
1 2 3 4 6、 、 、 、
1          
44
2 (L2) 
45
3 (L3)
463
4 (L4) 
4
47
6 (L6)
6
48
2、单一倒转轴： 5种
1
_
2
_
（m） 3
_
4
_
6
_
、 、 、 、
1(c) 1
49
m (P)2
50m
3 (L3C)
3
51
4 (L4
i)
4
52
6 (L6 ) i
6
53
3、旋转轴组合群： 6
种222、32、 422、 622、 23     和 432 
3L2 L33L2 L44L2 L66L2 3L24L3和3L44L36L2、 、 、 、 。
222 (3L2) 222
54
 
32 (L33L2)
32
55
422 (L44L2)
422
56
622(L66L2)
622
57
23 (3L24L3)  
23
58
432  (3L44L36L2)
59432
4、旋转轴、倒转轴与对称中心的组合群： 3种
(1) 奇次轴与对称中心的组合
A B B'
AC'
A'
C A'
  1
_
+ 1 = 1
_
  1
_
+ 3 = 3
_
 
(2) 偶次轴与对称中心的组合
60
2、m +C→2/m
2/m (L2PC) 2/m
61
4 +C→4/m
_
4,    
62
4/m (L4PC) 
63
4/m
6+C→6/m
6/m(L6PC)
6/
64
m
5、倒转轴与旋转轴的组合群： 10种
222→ 222
mm2 (L22P)
65
mm2
从223组合推导 223
3m (L33P) 
66
3m (L33P)
3 67m
从 223 组合推导2
_
2 3
_
组合 
L 33L23Pi
L33L23PC
3m
68
3m (L33L23PC) 
3m
69
224 224
4mm
704mm (L44P)
224 224
42m
7142m (L4
i2L22P)
226 226
6mm
72
6mm (L66P)
226 226
6m2
73
6m2 (L6
i3L23P)
233 233
2
3
74m 3  (3L24L33PC) m
233 233
2 3 ( 3)m
m
75
234组合→234
4 2234 3  ( 3 )m m
76
m m
4 2 (3L44L36L29PC)m3 m
m3m
77
234 234
3m m
78
234组合→234
234 43m
79
43m (3Li
44L36P)  
43m
80
倒转轴与旋转轴的欧拉组合
旋转轴的欧拉组合 倒转轴的欧拉组合
组合轴次 国际符号 对称元素 组合轴次 国际符号 对称元素
222 222 3L2 mm2 L22P
223 32 L33L2 3m L33P
222
223
L33L23PC
224 422 L44L2 4mm L44P
223 3m
224
Li
42L22P
226 622 L66L2 6mm L66P
224 42m
226
Li
63L23P
233 23 3L24L3 3L24L33PC
226 6 2m
233 3m
3L24L33PC
234 432 3L44L36L2 3L44L36L29PC
3m233
234 3m m
81
3L44L36L29PC
3Li
44L36P
234
234
3m m
43m
6、欧拉组合与对称中心的组合： 3种
mm2、222 + C → mmm
4mm、422 + C → 4/mmm
622 6mm 6m2 + C 6/mmm、 、 →
82mm2 (L22P)
+ C 
mm2 (L22P) 
mmm
83mmm (3L23PC)
4mm + C → 4/mmm
+ C
4mm (L44P)
4/mmm
844/mmm (L44L25PC)
+ C
622(L66L2)
6/mmm
856/mmm (L66L27PC)
m3m
Cu：4Cu
CaF2：4Ca，8F
金刚石 C
86
：8
Ge
Fe
b
Tb
Fe52Ge112T 117
Z=4
a=28.58A
V 23344 6A3= .
3Fm m
87
32种点群
单 旋转轴 (5种)• 一 :  
• 单一倒转轴: (5种) 
• 旋转轴的组合 （6种）
旋转轴与对称中心的组合•
• 倒转轴与对称中心的组合 （3个）
• 倒转轴与旋转轴的组合 （10个）
欧拉组合与对称中心的组合 （ 个）• 3
88
晶
单一旋 单一倒 旋转轴
32种点群所包括的对称元素及其国际符号
系
转轴 
Ln 
转轴 
Li
n 
+中心 
LnC 
复合旋转轴
LnL2 
单一轴面 
LnP‖ 
平面转轴 
Li
nP‖ 
复合轴面 
LnP‖L2
⊥ 
三 L1 Li
1
斜 (1) 
 
( 1
_
)  
单
斜
L2 
(2)
Li
2 
( 2
_
) 
L2PC
(2/m)     
正
交
   3L2 
(222) 
L22P 
(mm2)  3L23PC 
(mmm) 
3 3 3 2 3 3 2
三
角
L
(3) 
Li  
( 3
_
)  L 3L
(32) 
L 3P 
(3m) 
Li 3L 3P
( 3
_
m)  
四 L4 Li
4 L4PC L44L2 L44P Li
42L22P L44L25PC
方 (4) ( 4
_
) (4/m) (422) (4mm) ( 4
_
2m) (4/mmm) 
六
角
L6 
(6)
Li
6 
( 6
_
)
L6PC
(6/m)
L66L2 
(622)
L66P 
(6mm)
Li
63L23P 
( 6
_
m2)
L66L27PC 
(6/mmm)  
立
方
 
3L24L3 
(23) 
3L44L36L2  3Li
44L36P 
( 4
_
3 )
3L24L33PC 
(m 3
_
) 
3L44L36L29PC
89(432) 
m  
(m 3
_
m) 
§3-5  点群符号
1、 Hermann-Mauguin符号(国际符号)
 各晶系的特征方向 
晶系 第一特征方向 第二特征方向 第三特征方向 注 
三斜 [100]
单斜 [010]    
正交 [100] [010] [001] 
四方 [001] [100] [110]  
三角 [111]        菱面体坐标系
[001] [100] [210] 六角坐标系
[110]
六角 [001] [100] [210]  
立方 [001] [111] [110] 
90
立方晶系
3L44L36L29PC 4 23  ( 3m)m
m m
3L24L33PC 2 3 ( 3)m
m
91
Hermann-Mauguin符号(国际符号):
1) 与坐标轴的取向有关;
2) 对称元素的分布图像清晰 易于想象， ;
3) 从点群符号可以推导出该点群的全部对称元素
4 3
_
2
m m  
[001]
[111]
92[110]
3m m
[111]
93
2、熊夫利符号
1) 不同的符号及下标来表示特定的点群，其符
号比较系统;
2) 与坐标轴取向无关，对称元素的空间配置图
象不清晰 .
Cn: 旋转轴
C1、C2、C3、C4、C6 →1，2，3，4、6
C 直立的 次轴 水平反映面nh: n +
C1h、C2h、C3h、C4h、C6h→ m，2/m，，4/m、6/m
Cnv: n次轴 + 平行的反映面
C C C C → mm2 3m 4mm 6mm
94
2v， 3v， 4v、 6v ， ， 、
Dn：n 次轴 + 垂直于 n 次轴的 2 次轴 
D2、D3、D4、D6 → 222，32，422、622 
Dnh: Dn + 水平反映面 
/ /D2h，D3h，D4h、D6h→mmm，6m2，4 mmm、6 mmm
Sn：n 次倒转轴 
S2，S4、S6 → m，4 、6 
Dnd: 两相邻水平旋转轴的角平分线上有直立的反映面 
D2d、D3d → 4 2m、3m 
     Cs: 反映面，等同于 S2  
     Cni：n 次倒反轴，Ci=1
_
，C3i= 3
_
。 
T：四面体点群 
T、Th、Td → 23，m 3
_
、 4
_
3m 
O：八面体点群
95O、Oh → 432、m 3
_
m 
§3-6  劳厄群
11种劳厄群：与晶体衍射对称类型对应的有11种
晶系 三斜 单斜 正交 四方 三角 六角 立方 
劳厄群 -1 2/m mmm 4/m 4/mmm -3 -3m 6/m 6/mmm m-3 m-3m 
合并的点
群
1 2 222 4 422 3 32 6 622 23 432
  m mm2 -4 4mm  3m -6 6mm  -43m 
-42m -6m2    
 
96
6 1 m 
13 46 
32 (L33L2) 23 (3L 24L3) 432  (3L44L36L2)
2L33L23PC3m mmm (3L23PC)
点群：
1）32属于哪个晶系 特征方向是什么， ，
包含哪些对称元素？
2）23属于哪个晶系，特征方向是什么，
包含哪些对称元素？
3）2属于哪个晶系，特征方向是什么？
16