概要信息：

空间点阵: 将晶体内部的质点排列的周期性抽象成只有数学
意义的图形 (三维空间中周期性分布的无限点集). .
晶体中作周期性规律重复排列的那一部分内容
结构基元: 。
它是晶体中重复排列的基本单位,必须满足化学组
成相同、空间结构相同，排列取向相同和周围环
境相同的条件。
空间点阵+结构基元 晶体结构=
晶胞: 能完整反映晶体内部原子或离子在三维空间分布
之化学-结构特征的平行六面体单元。
35
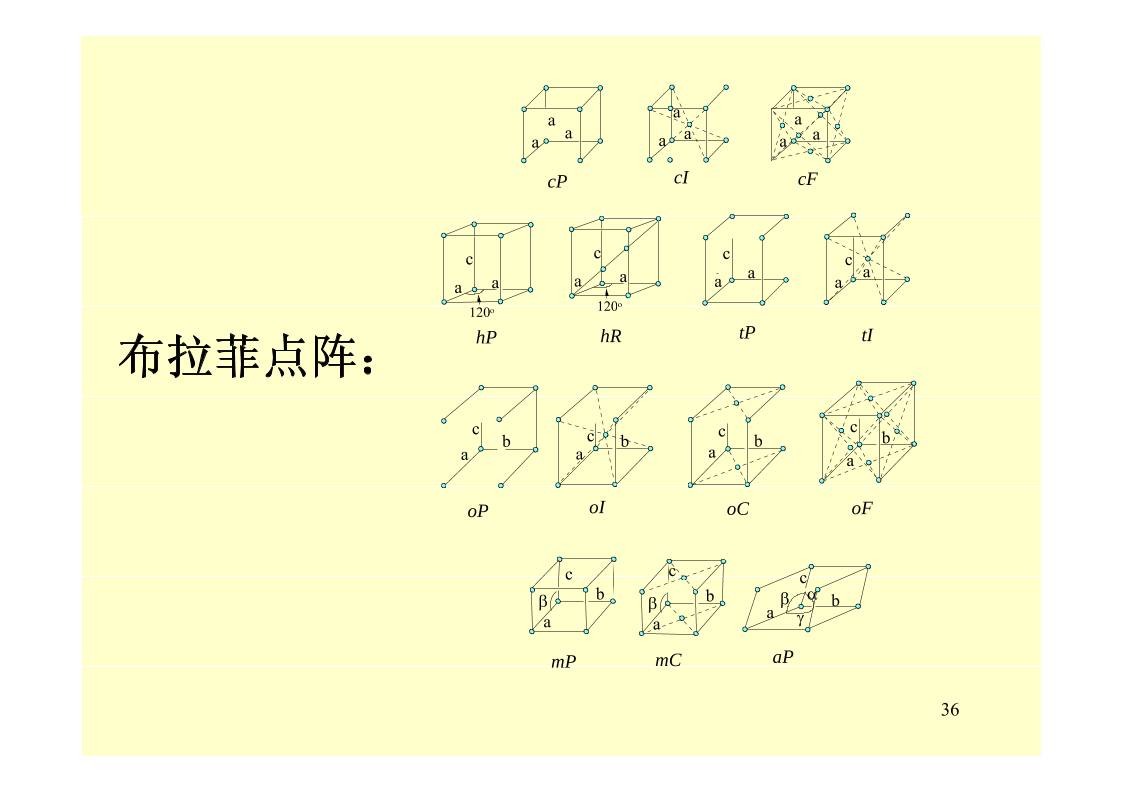
a a a
a a a a a a
cP cI cF
a a
c
a a
c c
a aa a
c

hP hR tP tI
布拉菲点阵：
a aa b bbc cc
a
b
c
oP oI oC oF
cc c
a
b b
a



mP mC aP
a
b
36
下面各式的意义
（010） <010>
：
{010}
[[010]] [010]
下面表示正确的是：
[222]（222）
[[222]] <222>
37
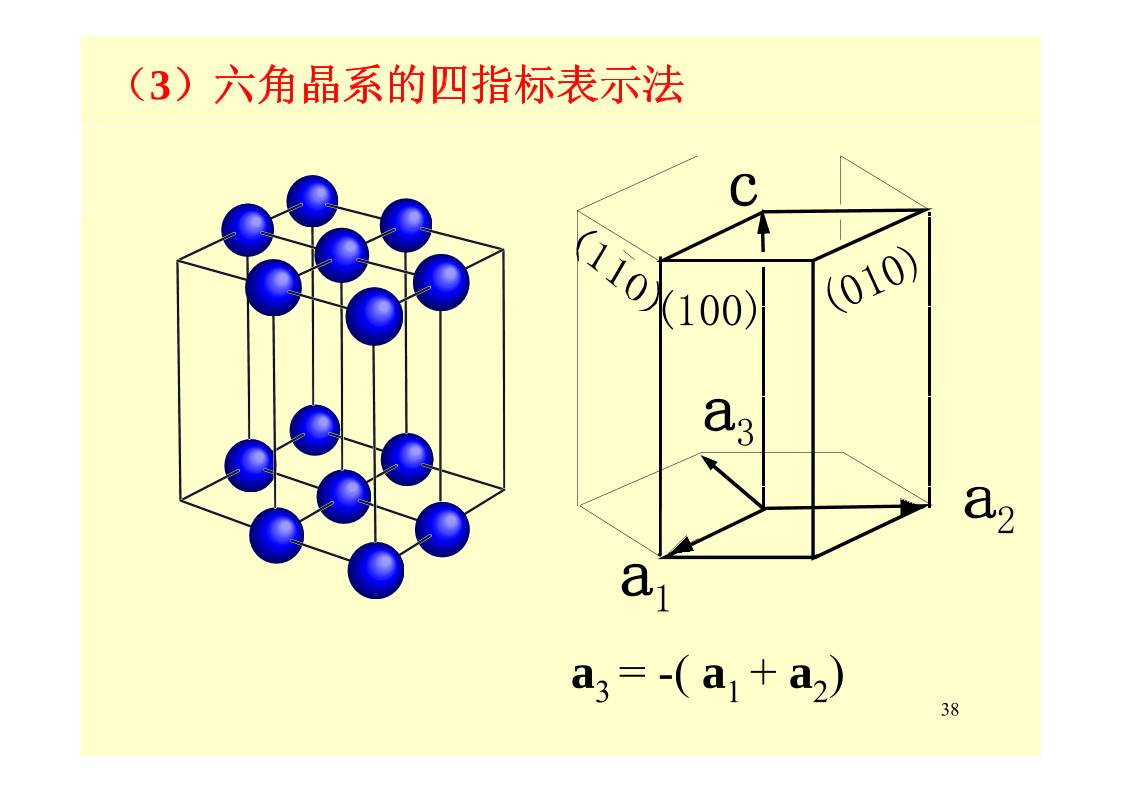
（3）六角晶系的四指标表示法
c
(100) (01
0)
a3
a
a2
1
a ( a + a )
38
3 = - 1  2
c
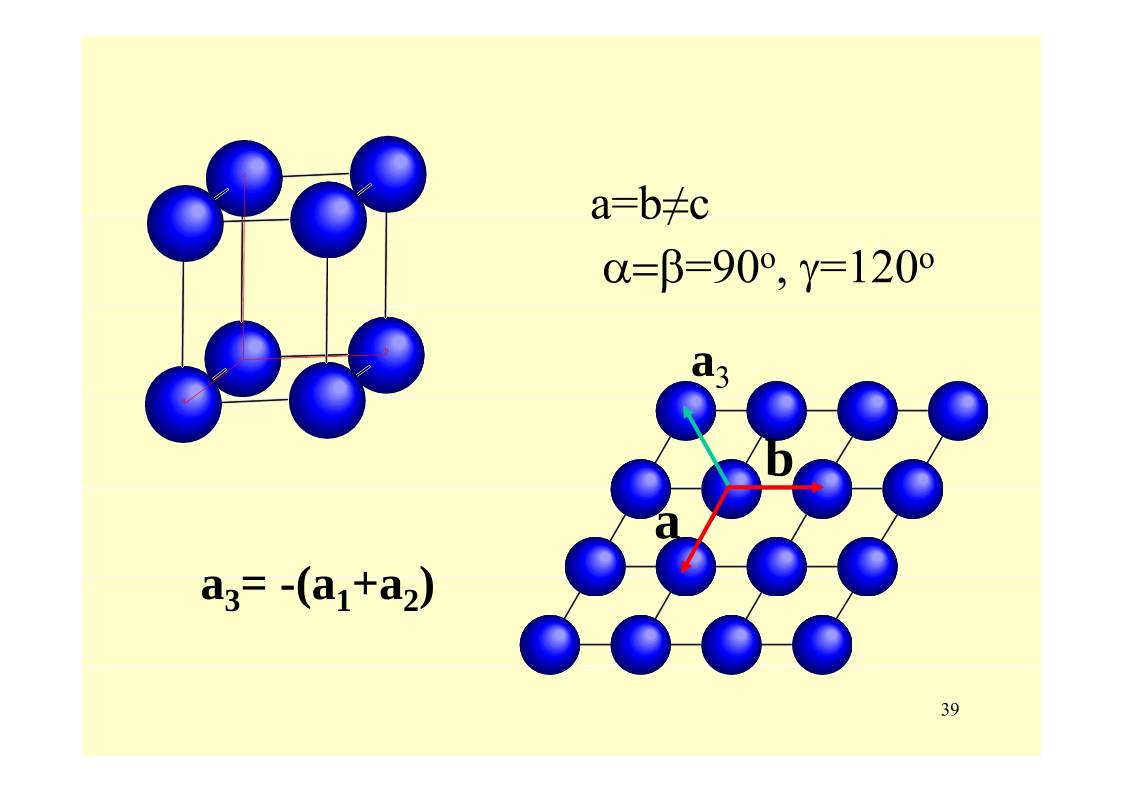
a=b≠c
=90o, =120o
b a3
a
b
a
a (a +a )3= - 1 2
39
a3
截距 :
(hkil)
1 2 3a a a c
O a
a2/k
, ,  ,  
h k i l
a a
C
B 2
a1/h a3/i
=
i h
3 1 AC = OC - OA
a1
1 1( )
h i i
    2
1
aaa3=-(a1+a2)
2
1 1 1 1 1( )
k i i i k
    3 1 2CB = OB - OC a a a a
1 1 1 1 1 1( ) : : ( ) ACXBC=0
h i i i k i
h+i k
  
40      i=h+k
h k+i

密勒指数为[uvw]，布喇菲-密勒指数[UVTW] 的关系
令：T = -(U+V)   
R = ua1 + va2 + wc
R = Ua1 + Va2 + Ta3 + Wc
= Ua1 + Va2 + [-(U+V)][- a1-a2 ] + Wc
= (2U+V) a1 +(U+2V) a2 + W c
u = 2U + V U = (2u - v) ⁄3    
v = U + 2V
w = W
V = (2v - u) ⁄3
T = -(U + V)
W = w
41
[110] [210]
[1120] [1010]
[100]
[2110]
u = 2U + V
v = U + 2V     
[120]
[0110] [110]
w = W
[010]
[1100]
U = (2u - v) ⁄3
(2 ) ⁄3
[1210] [010]
[1210]
V = v - u
T = -(U + V)
[110]
[1100] [120]
[ ]
W = w
[100]
[2110] [210]
[1010]
[110]
[1120]
0110
42
§2-2 倒易点阵
正点阵←→ 倒易点阵
1。倒易点阵的定义
cb
cba
a

*
acb *
cba 

b
bac 
*
43
ca 
* b c


a
a b c.
c
(b c  sin ) b c n .
        =  Sn
b
S a b c a n. .
αβ
a
a*b i
          = V γ
c s na*=
V

44
* * b*c* cos *b c.
2
* * ( ) ( )cos *=
b* * b* *V
  

b c c a a b. .
c c
( )( ) ( )( )= c a a b c b a a. . . .
2         
b*c*V
2 2b b
2
a ccos cos a ccos= ca sin absin V
 
 

V V
cos cos cos  
sin sin 

45
bca sin* 
V
cab sin*
b
V
sin

V
ac* 
sinsin
coscoscos*cos

 

sinsin
coscoscos*cos


 

2/1222 )(
sinsin
coscoscos*cos


 

b
46
coscoscos2coscoscos1   a cV
2。倒易点阵与正点阵的关系
（1）正点阵基矢与倒易点阵基矢之间的关系
cb 1)(* 


cba
aaa
ac 0)(* 


cba
aba  
* 1 * 0 * 0a·a = , a·b = , a·c = ;
b·a* = 0, b·b* = 1, b·c* = 0;
c·a* = 0, c·b* = 0, c·c* = 1.
同种正点阵基矢和倒易点阵基矢的
标量积为1，不同种正点阵基矢和倒易
47点阵基矢的标量积为零
cba 
* A=a* B=b* C=c*
cba 
* **)*( cba 
, , 
* 

B CA
* ** cba 

上式两边同时点乘a*，便得到：
A B C.
a* · ( a*)* = 1 → （a*)* = a
因此 正空间基矢也可用倒易空间基矢来表示:，
* * cba 

* *
***
acb
cba



* *
* **
bac
cba


48*** cba 

49
(010)晶面
单斜正交三角四方六角立方晶系
倒易单胞的基本参数
90                                  90                                 90                120           90                          
90                                                                            90               
 cba                   cba                              cba                           cba             cba           cba          
                                                                                                                                        
0o 





单胞参数
正点阵
11sin121
abcsin                      abc             cos23cos-1a                        ca              
2
3                     a           323223 


倒易点阵
单胞体积 ca
1                           
b
1               
cos23cos-1a
sin                          
a
1                     
3a
2                      
a
1                    b    
asin
                        
a
               
cos23cos-1a
                          
a
                     
3a
                      
a
                   a     
32
*
32
*





b
90                         90                      )
cos1
cos(cos                            90                     90                  90                        
csin
1                         
c
1                
cos23cos-1a
sin                          
c
1                         
c
1                       
a
1                     c    
001-000*
32
*







90                          90                       )
cos1
cos(cos                          90                     60                   90                       
-180                      90                      )
cos1
cos(cos                           90                     90                   90                       
001-000*
01-000 *









        90                               90                                    90                   60            90                         
90                                                     90                         
 cba            cba                     cba                         cba        cba       cba            
0000*0
*0***********0*****
******************





特征
50
立方，四方，正交
 =  =  = 90o
a*//a,   b*//b ,   c*//c; 
a*=1/a;   b*=1/b;  c*=1/c
51
（2）倒易点阵矢量与晶面间距
r*hkl = ha* + kb* + lc*   ⊥（h k l）面
r*hkl =1/dhkl。
c
C
/l [hkl]*
AB= OB - OA = b/k - a/h
r* AB
B
b
b/k
c
D
dhkl
hkl ·
= (ha* + kb* + lc*)·(b/k - a/h)= 0
O
同理，r*hkl ·AC = 0
n = r* / r*
A a
a/h
hkl hkl
dhkl = OD = a/h·n = 1/ r*hkl
52
（3）倒易点阵晶胞体积等于正点阵晶胞体积的倒数
正点阵晶胞体积V = a·b X c
倒易点阵晶胞体积 V* = a*·b*X c*
V V* = (a·bX c) (a*·b*X c*)
*** cabaaa  1 0 0
***
****
ccbcac
cbbbab

VV = 0 1 0
0 0 1
=1
倒易点阵晶胞体积等于正点阵晶胞
体积的倒数
53
(4) 点阵平面与晶带轴的对应关系
[uvw]
[u v w]晶带轴：
 
R = u a +vｂ＋ wｃ
如果晶面(hi ki li) //R
P(hi ki li)面的法线都垂直于R
(h k l )面的倒易点在同i i i
一平面P上
[uvw]为P平面的法线
54
G*i = hi a* +ki b* + li c* //(hi ki li) 面的法线方向
G* 所代表的倒易点构成了一个倒易点阵平面ｉ
这个倒易点阵平面的指数为(u v w)*，它的法线方
向为[u v w]。
[ ] ( )*u v w  平行于 u v w  倒易面的
法线方向
55
§2-3 晶带定律
1。晶带定律的定义
晶体中若干晶面平行于同一晶向[uvw]时，这些
晶面便组成了一个晶带 这些晶面所平行的晶向叫做，
晶带轴, [uvw]晶带
[uvw]的方向: ruvw = u a + v b + w c
（hkl）面的法线方向: r* = h a* + k b* + l c*hkl ,
(h a* + kb* + l c*)·（u a + v b + w c) = 0
h u + k v + l w = 0
56
2。晶带定律的应用
如果（h1k1l1）、（h2k2l2）同属于[uvw]晶带
[uvw]必定是（h1k1l1）、（h2k2l2）的交线：
h u + k v + l w = 0 h1u + k1v = -l1w 
1 1 1
h2u + k2v + l2w = 0 h2u + k2v = - l2w
1 1 1 1l w k k l
w

1 1 1 1h l w l h
2 2 2 2l w k k l
u
h k h k

  2 2 2 2
w
h l w l h
v
h k h k

 
1 1 1 1
2 2 2 2h k h k
1 1 1 1
2 2 2 2h k h k
57
h k1 1
2 2
w
h k
令：
111111 khhllk
   ::  w :v:u
222222 khhllk

h1   k1   l1   h1   k1    l1
h2   k2   l2   h2   k2    l2 
u  v  w
58
(hkl)晶面同时属于[u1v1w1]、[u2v2w2]两个晶带:
u1h + v1k + w1l = 0
u2h + v2k + w2l = 0
111111 vuuwwv→  ::  l :k :h
222222 vuuwwv

例:（h1 k1 l1）和 (h2 k2 l2)同属于 [u v w] 晶带轴：
(h u + k v + l w)* p = 0;1 1 1
(h2 u + k2 v + l2 w) * q = 0
(p h1 + q h2) u +(p k1 +q h2) v + (p l1 +q l2) w = 0
即 ( p h1 + q h2 p k1 +q h2 p l1 +q l2) 也属[u v w] 晶带轴。
59
c
B
A
O b
a
OA:[201] 2 01201     
OB: [122] 1 2212 2 OAB面:(         )234
60
 
234
(101)
(011)
A
B
E
FS AB//FEC
D AF//CD
(210)
AB,FE: (101) (010)=[101]
AF,CD: (011) (210)=[122]
61S=[101] [122] (232) 
§2-4 坐标变换
4。非初基胞与初基胞之间的变换
面心点阵的初基胞基矢（a' b' c'）与非初基胞基
2/12/10'  aac
矢（a b c）的关系式为：
  2/102/1' 









 bb
02/12/1'  cca'b'
'111 
b
c'  '111 






 




 b
a
b
a
a '111   cbc
62
体心点阵 :
a'c 2/12/12/1'  aa
b'
  
2/12/12/1
2/12/12/1
'
'




















 c
b
c
b

b
'
'
101
110


















b
a
b
a
c'a '011  cc
63
C心点阵
c 02/12/1
02/12/1
'
'


















b
a
b
a
c'
 
100' 

 cc
b '011







 



 aa
'
b'  
'
' 
100
011















bb
aa cc
64
5。用六角坐标系表示三角晶系
常用六角坐标系来描述三角晶系。使三角晶系中
的3次轴为六角坐标系的C轴，此时的晶胞不再是初
基胞，而是三重晶胞. 
ch ch
1/3 2/3 2/3
C C
， ，
ar
brcr
B B bh
2/3，1/3，1/3
a
bh
A
O O
A
ah
65
h
ah = ar - br 011   h aa
bh = br - cr   
111
110





















r
r
h
c
b
c
b
ch = ar + br + cr
a = (2ah + bh + ch)/3
rh
3/13/13/2 r
br = (-ah + bh + ch)/3   3/13/13/1


















h
h
r
r
b
a
b
a
cr = (-ah -2bh + ch)/3
3/13/23/1   hr cc
面指数关系
hh = hr - kr
hr = (2hh + kh + lh)/3
kh = kr - lr
l h + k + l
kr = (-hh +kh + lh)/3
l = (-h - 2k + l )/3
66
h = r  r  r r  h h  h  
晶向指数的关系
uh = (2ur - vr - wr)/3
( 2 )/3
ur = uh +vh
v = u + v + wvh = ur + vr - wr
wh = (u + v + w )/3
r - h h h
wr = -vh + wh r  r  r  
ah·ah = (ar - br)·(ar - br)
ah
2 = ar
2 + br
2 - 2arbrcosγ
 )cos1(2  raah
 )2cos3(1ac rh 
67
§2-5晶体几何学公式
晶面间距，晶面间夹角，点阵矢量长度，点阵矢量
夹角计算公式
21
2
21
2
21
2222
21
222
21
222
21
2222
21
2222222
21
2
22222222
2
2
cos2sinsinsinAcos(cos2sinl
cos    r                                                               
V
Acos        sinsin[1g   
wwcvvbuuaBbcvwballcakkcbhhhkabba
rr
Bwcvbua
gg
cakcbh
V



三斜
21212121
22222222
21212121
2
21212121
2
)coscos2cos
cos)                                                                     ))(coscos(cosbca           coscoscos1(             
cos)                        cos2                         ))(coscos(coscab                         )coscos(cos2                  
cos)                        cos2                       ))(coscos(cosabc            )coscos(cos2)cos-                   
                                            
uvvab(ulkklcbaV
wuuca(wabuvhllhhlac
vwwbc(vcawukhhkklbc








212121
2
21
2121
2
21
2
21
2
21
2222222
22
21
2
21
22
21
22
2
2
2
22
2
2
cos)                  cos2                                                   /]
sin
cos)(-                                                      
sin
cos2-                    
 ,cos      r                                   
sinsin
[cos                  
sinsin
g    
                   
wuuac(wwwcacuwgg
ac
lhhl
ac
hl
vvbuuaC
rr
Cwcvbua
c
ll
b
kk
a
hh
c
l
b
k
a
h












单斜
222222222
21
2
2121
2
22
212
21
2121
2
21
2222
2121212122
2
2
22
2
///
)(
2
a-                                                                                                      /}                                                                                                 
)(  ,cos            )(r                        )](
2
1[
3
4{cos                         
3
)4g    
bllbkkhhlkh
wwcuvvuwcgg
c
ll
vvuuaD
rr
Dvuvuahkkhkkhh
ac
l
a
khk(h




 六角
212121
2
22222212121
222
2
21
21
2
2121
2
222222
21
2
21
2
2121
2
2
2
22
2
21
2121212222222
21
212121
222
2
)(a)(
)(acos         )(r                                     //)cos                                        g    
acos        r                                 cos                                      g    
wwvvuullkkhhlkh
rr
wwcvvuuwcvua
gg
cllakkh(h
c
l
a
kh
rr
wwcvvuulcvbua
gg
ca
cba











立方
四方
正交
68
2121
22 cos           r                                                 cos                                        g   
rr
wvua
ggaa
 
６．等效原理 对称性
应用晶面间距公式就可得到晶面族所包括的
晶面指数。
同一晶面族的各晶面的面间距相同。改变晶
面指数的顺序和／或正负号时，如果晶面间距
不发生改变 这些晶面则属于同一晶面族，
应用晶向长度公式就可得到晶向族所包括的
晶向指数。
晶向族的各晶向的长度相 改变晶向同一 同。
指数的顺序和／或正负号时，如果晶向的长度
69不发生改变，这些晶向则属于同一晶向族
§2-6晶体的极射赤面投影
001
011
101
101111011
1。球面投影
111
111
111
110
参考球，极球；
极010
110 100 110
010
晶面的 点；
大圆 小圆
111
011
111
111
,
同 晶面族？101
001
101
111 011 一
同一晶带各晶面的极点必定分布在同
一大圆上 垂直于此大圆的直径则是该晶
70
，
带的晶带轴
2。极射赤面投影
N
BC
大圆弧；
A
D
B'C'
投 影面
小圆弧 ;
A'
D' E'
E 投影基圆
S
同一晶带轴的晶面的极射赤面投影
71点位于同一大圆弧上。
3。标准极图
210
100
210
110
211
201
211
110
111121 212 101
111
212
121
120
221221
120
010 010021011012021 011 012
122112102112122
121
111 111
121
102 112 122
001
112
122
110
221
211
201211
110
221
120 212 101 212 120
100
210210
72立方晶体（001）标准极图
73立方晶体（111）标准极图
复习: 1. 正点阵基矢与倒易点阵基矢之间的关系
同种正点阵基矢和倒易点阵基矢的标量积为1 不，
同种正点阵基矢和倒易点阵基矢的标量积为零
[uvw]的方向: ruvw = u a + v b + w c
2、晶带定律
(hkl)面的法线方向: r*hkl = h a* + k b* + l c*,
(h a* + kb* + l c*)·(u a + v b + w c) = 0
h u + k v + l w = 0
h1   k1   l1   h1   k1    l1 两个晶面同属于
h2   k2   l2   h2   k2    l2 
一个晶带[uvw]
(112) (232)
u  v  w
, 
一个晶面同属于
两个晶带[uvw]
U1 V1 W1 U1 V1 W1
U2 V2 W2 U2 V2 W2
h k l
[321], [111]
           
晶面间距通用公式：
2
简立方： (cP): a=4 Å, 面间距：(111)
体心立方：cI : a= 4 Å, 面间距：(111) 
简立方
体 立方/面 立方晶面间距 /心 心 : d简立方 2 
（222）
晶体几何学 （X-射线衍射结晶学不能简化）
3
极射赤面投影
N
BC
A
D
B'C'
投 影面
A'
D' E'
E 投影基圆
S
同一晶带轴的晶面的极射赤面投影点位于
同 大圆弧上
4
一 。