概要信息：

目　录
第一章　信号与系统的基本概念 （１）
!!!!!!!!!!!!!!!!!!!!!!!!!!!
第二章　连续时间系统时域分析 （４）
!!!!!!!!!!!!!!!!!!!!!!!!!!!
第三章　傅里叶变换，连续时间系统的频域分析 （７）
!!!!!!!!!!!!!!!!!!!!
第四章　傅里叶变换用于通信系统 （１１）
!!!!!!!!!!!!!!!!!!!!!!!!!
第五章　拉普拉斯变换，ｓ域分析 （１４）
!!!!!!!!!!!!!!!!!!!!!!!!!!
第六章　离散系统的时域分析 （１９）
!!!!!!!!!!!!!!!!!!!!!!!!!!!
第七章　离散时间系统的ｚ域分析 （２１）
!!!!!!!!!!!!!!!!!!!!!!!!!
第八章　离散傅里叶分析 （２５）
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
第九章　系统的状态变量分析 （２８）
!!!!!!!!!!!!!!!!!!!!!!!!!!!
第一章　信号与系统的基本概念
【考情分析】
本章的考题主要涉及信号与系统的基本概念等，这些内容在以往各高校研究生统考中都会考查
到，难度不大。需要重点理解和掌握：
·信号的各种分类及其特性
·冲激函数的性质
·冲激函数变换得到的性质以及与其他函数的运算
·线性时不变系统的四种特性
考点１：信号的各种分类及特性
１．【北京航空航天大学】
试确定下列信号周期
（１）ｘ（ｔ）＝３ｃｏｓ（４ｔ＋π３）　　 （　）
（Ａ）２π　　　　　　 （Ｂ）π　　　　　　　（Ｃ）π２　　　　　　　（Ｄ）
２
π
（２）ｘ（ｎ）＝２ｃｏｓ（ｎπ４）＋ｓｉｎ（
ｎπ
８）－２ｃｏｓ（
ｎπ
２ ＋
π
６）　　　（　 ）
（Ａ）８　　　　　　　（Ｂ）１６　　　　　　　（Ｃ）２　　　　　　　（Ｄ）４
２．【北京工业大学】
试证明两个奇信号或者两个偶信号的乘积是一个偶信号；
一个奇信号和一个偶信号的乘积是一个奇信号。
考点２：冲激函数及阶跃函数的性质及应用
１．【华侨大学 ２０１２】
∫
ｔ
－
!
２ｃｏｓ（τ＋π６）δ（τ－
π
６）ｄτ＝ 。
２．【武汉科技大学】
下列各表达式中错误的是 （　）
（Ａ）δ′（ｔ）＝－δ′（－ｔ） （Ｂ）δ′（ｔ－ｔ０）＝δ′（ｔ０－ｔ）
（Ｃ）∫!－
!
δ′（ｔ）ｄｔ＝０ （Ｄ）∫
ｔ
－
!
δ′（τ）ｄτ＝δ（ｔ）
３．【北京邮电大学，２０１１】
与δ（ｔ２－４）相等的表达式为 （　）　
—１—
郑君里《信号与系统》名校真题解析及典型题精讲精练
Ａ．１２δ（ｔ－２） Ｂ．１２ δ（ｔ－２）＋δ（ｔ＋２
[ ]）
Ｃ．１４δ（ｔ－２） Ｄ．１４ δ（ｔ－２）＋δ（ｔ＋２
[ ]）
４．【西安电子科技大学】
∫
!
－
!
（ｔ２＋２）［δ′（ｔ－１）＋δ（ｔ－１）］ｄｔ＝ 。
Ａ．０ Ｂ．１ Ｃ．３ Ｄ．５
５．【西安电子科技大学期末２００８年】
∫
!
－
!
（ｔ－３）δ（－２ｔ＋４）ｄｔ＝ 。
Ａ．－１ Ｂ．－０．５ Ｃ．１ Ｄ．０．５
考点３：基本函数画图
１．【北京交通大学】
若ｆ（ｔ）波形图如图所示，试画出ｆ（－０．５ｔ－１）的波形。
２．【北京邮电大学，２０１１】
信号ｆ（－２ｔ＋３）如图所示，试画出ｆ（ｔ）波形。
３．【西安电子科技大学】
已知波形如图所示，ｇ（ｔ）＝ｄｄｔｆ（ｔ），试画出ｇ（ｔ）和ｇ（２ｔ）波形。
—２—
考点４　系统的性质及分类
１．【北京航空航天大学】选择题
已知系统
（Ａ）ｒ（ｔ）＝２ｅ（ｔ）＋３ （Ｂ）ｒ（ｔ）＝ｅ（２ｔ）
（Ｃ）ｒ（ｔ）＝ｅ（－ｔ） （Ｄ）ｒ（ｔ）＝ｔｅ（ｔ）
试判断上述哪些系统满足下列条件：
（１）不是线性系统的是
（２）不是稳定系统的是
（３）不是时不变系统的是
（４）不是因果系统的是
２．【重庆大学】
判断下列系统的因果性，线性及时不变性，并说明理由。
其中说明理由。其中ｕ（ｔ）为单位阶跃函数。
（１）ｙ（ｔ）＝ｆ（１－ｔ）　　　　（２）ｙ（ｔ）＝ｓｉｎｆ（ｔ[ ]）ｕ（ｔ）
３．【北京邮电大学２０１１】
已知某线性时不变系统在相同初始条件下，当激励为ｅ１（ｔ）时的
完全响应为ｒ１（ｔ）＝（２ｅ
－ｔ－ｅ－３ｔ）ｕ（ｔ），当激励为０．５ｅ１（ｔ）时的完全响应
为ｒ２（ｔ）＝（ｅ
－ｔ－２ｅ－３ｔ）ｕ（ｔ），试用时域分析方法求在相同初始条件下
当激励为２ｅ１（ｔ－１）时的完全响应ｒ３（ｔ）
４．【华中科技大学】
一线性时不变系统有两个初始条件：ｘ１（０）和ｘ２（０）。若
（１）ｘ１（０）＝１，ｘ２（０）＝０时，其零输入响应为ｙｚｉ１（ｔ）＝（ｅ
－ｔ＋ｅ－２ｔ）ε（ｔ）
（２）ｘ１（０）＝０，ｘ２（０）＝１时，其零输入响应为ｙｚｉ２（ｔ）＝－（ｅ
－ｔ－ｅ－２ｔ）ε（ｔ）
已知激励为ｆ（ｔ），ｘ１（０）＝１，ｘ２（０）＝－１，时，其全响应为（２＋ｅ
－ｔ）ε（ｔ），
试求激励为２ｆ（ｔ），ｘ１（０）＝－１，ｘ２（０）＝－２时的全响应ｙ（ｔ）
—３—
郑君里《信号与系统》名校真题解析及典型题精讲精练
第二章　 连续时间系统时域分析
【考情分析】
本章的考题主要涉及连续时间系统的时域分析，这些内容在以往各高校研究生统考中都会考查
到，各类题型都会出现。需要重点理解和掌握：
·线性时不变系统的零输入响应和零状态响应以及全响应
·稳态响应和瞬态响应
·单位冲激响应和单位阶跃响应的求解
·卷积的交换律、分配律和结合律
·卷积的积分性质和微分性质，与冲激函数和阶跃函数等进行卷积的特有性质
考点１　线性时不变连续系统的时域经典解
１．【中山大学】
系统的微分方程为ｙ″（ｔ）＋３ｙ′（ｔ）＋２ｙ（ｔ）＝ｆ′（ｔ）＋３ｆ（ｔ），已知ｆ（ｔ）＝ｕ（ｔ），初始状态为ｙ（０－）
＝１，ｙ′（０－）＝２，试求系统的全响应。并指出零输入响应、零状态响应、自然响应及强迫响应。
考点２　卷积积分的定义及性质
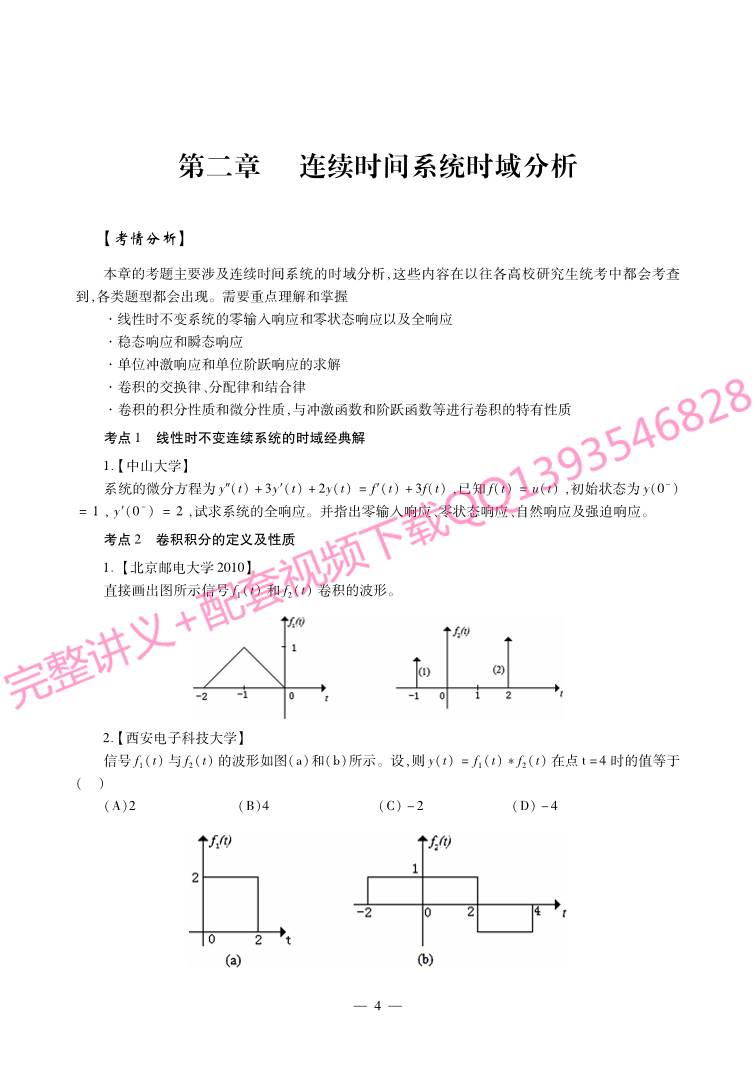
１．【北京邮电大学２０１０】
直接画出图所示信号ｆ１（ｔ）和ｆ２（ｔ）卷积的波形。
２．【西安电子科技大学】
信号ｆ１（ｔ）与ｆ２（ｔ）的波形如图（ａ）和（ｂ）所示。设，则ｙ（ｔ）＝ｆ１（ｔ）ｆ２（ｔ）在点ｔ＝４时的值等于
（　）
（Ａ）２ （Ｂ）４ （Ｃ）－２ （Ｄ）－４
—４—
３．【浙江大学】
已知ｆ（ｔ）和ｈ（ｔ）如图（ａ）和（ｂ）所示，求ｙ（ｔ）＝ｆ（ｔ）ｈ（ｔ）
４．【北京航空航天大学】
计算下列卷积。
ｅ－ｔｕ（ｔ） δ（ｔ）＋２δ′（ｔ）－δ″（ｔ[ ]）ｔｕ（ｔ）
考点３　利用卷积积分求系统的冲激响应，阶跃响应和零状态响应
１．【北京邮电大学２０１１】判断题
（１）冲激信号是一个高且窄的尖峰信号，它具有有限的面积和无限的能量。
（２）已知两个级联的子系统的单位冲激响应分别为ｈ１（ｔ）和ｈ２（ｔ），则激励为ｅ（ｔ）时整个系统的
零状态响应为ｅ（ｔ）·ｈ１（ｔ）·ｈ２（ｔ）。
（３）阶跃响应是线性时不变系统对阶跃信号的响应。
（４）若ｘ（ｔ）的傅里叶变换为Ｘ（ｆ），则Ｘ（０）＝ｘ（ｔ）的面积 ＝∫
!
－
!
ｘ（ｔ）ｄｔ
（５）理想低通滤波器的阶跃信号的响应不是单调的、并有过冲和振动。
２．【武汉科技大学】
已知一个线性时不变系统的阶跃响应为ｓ（ｔ）＝２ｅ－２ｔｕ（ｔ）＋δ（ｔ），当输入ｆ（ｔ）＝３ｅ－ｔｕ（ｔ）时，系
统的零状态响应ｙｆ（ｔ）等于（　）。
Ａ．（－９ｅ－ｔ＋１２ｅ－２ｔ）ｕ（ｔ） Ｂ．（３－９ｅ－ｔ＋１２ｅ－２ｔ）ｕ（ｔ）
Ｃ．δ（ｔ）＋（－６ｅ－ｔ＋８ｅ－２ｔ）ｕ（ｔ） Ｄ．３δ（ｔ）＋（－９ｅ－ｔ＋１２ｅ－２ｔ）ｕ（ｔ）
３．【北京理工大学】
系统如图（ａ）所示，其子系统冲激响应ｈ１（ｔ）＝δ（ｔ＋１）－δ（ｔ）ｈ３（ｔ）＝δ（ｔ）－δ（ｔ－２），子系统
ｈ２（ｔ）的输入、输出如图（ｂ），要求在时域回答：
—５—
郑君里《信号与系统》名校真题解析及典型题精讲精练
（１）子系统冲激响应ｈ２（ｔ）；
（２）系统ｅ（ｔ）→ｒ（ｔ）的冲激响应ｈ（ｔ），画出其波形；
（３）当ｅ（ｔ）＝ｕ（ｔ）时系统输出ｒ（ｔ），画出其波形。
４．【西北工业大学】
系统的输入输出关系为ｙ（ｔ）＝∫
ｔ
－
!
ｅ－（ｔ－τ）ｆ（τ－２）ｄτ，求系统单位冲激响应ｈ（ｔ）。
—６—
第三章　傅里叶变换，连续时间系统的频域分析
【考情分析】
本章的考题主要涉及连续时间系统的频域分析，也就是利用傅里叶变换的性质求解，这些内容在
以往各高校研究生统考中出现频率较高，有部分题目难度偏高。需要重点理解和掌握：
·傅里叶级数求解
·傅里叶变换以及傅里叶反变换
·傅里叶微分、积分性质、时域平移、频域平移性质
·利用傅里叶变换求系统响应
·利用傅里叶变换分析输出信号的频谱
考点１　傅里叶级数
１．【北京交通大学，２００６】
周期信号ｆ（ｔ）的双边频谱如图所示，写出ｆ（ｔ）的三角函数表示式。
２．【北京邮电大学，２００９】
已知信号ｘ（ｔ）＝４ｃｏｓ（１０πｔ＋π４）－６ｃｏｓ（２０πｔ＋
π
６）＋２ｓｉｎ（４０πｔ＋
π
３）
（１）画出双边幅度和相位谱图；
（２）计算信号的功率。
３．【北京邮电大学】
已知冲激序列δＴ（ｔ）＝∑
!
ｎ＝－
!
δ（ｔ－ｎＴ），其三角函数形式的傅里叶级数为 。
考点２　傅里叶变换及其性质
１．【北京邮电大学，２０１０】
设ｆ（ｔ）的频谱函数为Ｆ（ｊω），则ｆ（－ｔ２－１）的频谱函数等于 。
２．【电子科技大学】
信号ｆ（ｔ）的傅里叶变换Ｆ（ω）如图所示。不求ｆ（ｔ），计算下列各式。
—７—
郑君里《信号与系统》名校真题解析及典型题精讲精练
（１）求ｆ（０）。
（２）计算∫
!
－
!
ｆ（τ）ｄτ
（３）计算∫
!
－
!
ｆ（ｔ）ｓｉｎ２ｔ
πｔ
ｄｔ
３．【西安电子科技大学，２００６】
已知信号ｆ（ｔ）如图所示，其傅里叶变换为Ｆ（ｊω）＝ Ｆ（ｊω）ｅｊφ（ω）。
（１）求Ｆ（ｊ０）的值
（２）求积分∫
＋
!
－
!
Ｆ（ｊω）ｄω
（３）求信号能量Ｅ。
４．【浙江大学】
求信号ｆ（ｔ）＝
ｃｏｓω０ｔ，ｔ＜
τ
２
０，
{
其他
　的Ｆ（ｊω）。
５．【华中科技大学】
若ｆ（ｔ）的傅里叶变换为Ｆ（ｊω），则
ｙ（ｔ）＝ｔｄ
ｄｔｆ（ａｔ）ｆ（ｔ－ｂ
[ ]{ }） ｅｊω０ｔ的傅里叶变换Ｙ（ｊω）＝ 。
６．【浙江大学，２００３】
求Ｆ（ｊω）＝ １
ｊω＋１δ（２ω）＋ｅ
－ｊ２[ ]ω 的反变换ｆ（ｔ）。
７．【西安电子科技大学，２００６】
频谱函数Ｆ（ｊω）＝２ｕ（１－ω）的傅里叶反变换ｆ（ｔ）＝ 。
８．【西安电子科技大学】
设ｙ（ｔ）＝ｆ（ｔ）ｈ（ｔ），ｒ（ｔ）＝ｆ（３ｔ）ｈ（３ｔ），并且ｆ（ｔ），ｈ（ｔ）
—８—
的傅里叶变换分别为Ｆ（ｊω），Ｈ（ｊω）。试证明：ｒ（ｔ）＝Ａｙ（Ｂｔ），并求出Ａ和Ｂ的数值。
考点３：系统函数的求解及应用
１．【北京邮电大学，２００７】
如图所示，理想 －π２ｒａｄ相移器的频响特性定义为
Ｈ（ｊω）＝
ｅ－ｊ（
π
２）ω＞０
ｅｊ（
π
２）ω＜
{
０
（１）求该相移器的冲激响应ｈ（ｔ）
（２）当ｘ（ｔ）＝ｃｏｓω１ｔ时，求该相移器对ｘ（ｔ）的稳态响应ｙ（ｔ）。
２．【北京邮电大学，２０１０】
如图描述了一个多天线阵列，利用该阵列可实现波束赋形，使来自不同方向的无线电波有不同的
接收增益，实现无线信号的定向接收。假设各天线沿水平方向放置，各天线间距为ｄ。平面波ｅ（ｔ）＝
ｅｊω０ｔ按方向角θ斜入射到达天线阵。如果第１个天线测量得到的信号是ｅ（ｔ），则第二个天线测量得到
的信号为ｅ（ｔ－τ（θ）），其中τ（θ）＝ｄ·ｓｉｎθｃ ，ｃ是光速。一次类推，第ｋ个天线测量得到的信号为ｅ（ｔ
－ｋτ（θ））。对天线阵列测量得到的信号进行加权合并，得到天线矩阵的输出 ｒ（ｔ）＝∑
Ｎ－１
ｋ＝０
ｗｋｅ（ｔ－
ｋτ（θ））。
（１）求出该天线矩阵的频率响应
（２）假设如射信号的工作频率满足
ω０ｄ
ｃ ＝π，当ｗ０ ＝ｗ１ ＝０．５，Ｎ＝２时，求出并画出天线阵对
不同方向来波的幅度增益图（－π＜θ＜π）。
３．【中国科学技术大学】
已知单位冲激响应为ｈ（ｔ）＝
ｓｉｎω０（ｔ－１[ ]）ｓｉｎ２ω０（ｔ－１[ ]）
π２（ｔ－１）２
的连续时间 ＬＴＩ系统，试求它的频
—９—
郑君里《信号与系统》名校真题解析及典型题精讲精练
考点４　 连续时间系统的频域分析
１．【西安电子科技大学】
已知系统的频率响应为
Ｈ（ｊω）＝
ｅｊ
π
２，－６＜ω＜０
ｅ－ｊ
π
２，０＜ω＜６
０，





ｏｔｈｅｒｗｉｓｅ
系统激励为ｆ（ｔ）＝ｓｉｎ３ｔｔｃｏｓ５ｔ，求系统的响应ｙ（ｔ）。
２．【上海交通大学】
如图所示系统，其中ｘ（ｔ）＝∑
!
ｎ＝－
!
ｅｊｎｔ，ｓ（ｔ）＝ｃｏｓｔ，
Ｈ（ｊω）＝
ｅ－ｊ
π
３，ω "
２．５
０，ω ＞２．
{ ５
。
求：（１）ｘ（ｔ）和ｆ（ｔ）的频谱图
（２）ｙ（ｔ）
３．【西北工业大学】
求信号ｆ（ｔ）＝２ｃｏｓ１０００ｔ×ｓｉｎ５ｔ
πｔ
的能量Ｗ。
４．【西北工业大学】
如图（ａ）所示系统，已知输入信号ｆ（ｔ）的Ｆ（ｊω）＝Ｇ４（ｊω），子系统函数Ｈ（ｊω）＝ｊｓｇｎ（ω），求系
统的零状态响应ｙ（ｔ）。
—０１—
第四章　傅里叶变换用于通信系统
【考情分析】
本章的考题主要涉及傅里叶变换在通信系统中的应用，这些内容在以往各高校研究生统考中出
现频率相对偏低，一般出现在大题中，难度偏大。需要重点理解和掌握：
·希尔伯特变换
·时域抽样定理
·频域抽样定理
·奈奎斯特定理
·信号的调制与滤波
·信号的无失真传输
考点１　希尔伯特变换
１．【电子科技大学】
今有 Ｌ[ ]· 表示希尔伯特运算，ｈ[ ]ｔ为希尔伯特变换器的单位冲激响应，即有：Ｌｆ（ｔ[ ]） ＝
ｈ（ｔ）ｆ（ｔ），若ｈ[ ]ｔ的傅里叶变换为Ｈ（ω）＝ｊｓｇｎ（ω），ｆ（ｔ）为实值信号。
（１）求出ｈ（ｔ）；
（２）证明：（１）ＬＬｆ（ｔ[ ]{ }） ＝－ｆ（ｔ）
（２）∫
!
－
!
ｆ（ｔ）Ｌｆ（ｔ[ ]）ｄｔ＝０
考点２　取样定理
１．【武汉科技大学】
有限频带信号ｆ（ｔ）的最高频率为１００Ｈｚ，若对下列信号进行时域采样，求得最小采样频率ｆｓ。
１．ｆ（３ｔ）　 ２．ｆ２（ｔ）　 ３．ｆ（ｔ）ｆ（２ｔ）　 ４．ｆ（ｔ）＋ｆ２（ｔ）
２．【中国科学院，２００６】
如图（ａ）所示的连续时间信号抽样传输系统，已知系统的输入信号ｘ（ｔ）＝ｓｉｎ
２（４π×１０３ｔ）
π２ｔ２
，抽样
间隔Ｔ＝０．１ｍｓ图中的信道滤波器是一个实的升余弦滚降带通滤波器，其频率响应 ＨＢＰ（ｆ）如图（ｂ）
所示试求：
（１）ｘ（ｔ）的频谱Ｘ（ω），并概画出Ｘ（ω）以及ｘＰ（ｔ）、ｙ（ｔ）的频谱ＸＰ（ω）、Ｙ（ω）。
（２）试设计由系统输出ｙ（ｔ）恢复出ｙ（ｔ）恢复出ｘ（ｔ）的系统，画出该恢复系统的方框图，并给出
其中所用系统的系统特性（例如，滤波器的频率响应等）。
—１１—
郑君里《信号与系统》名校真题解析及典型题精讲精练
３．【国防科技大学】
对一最高频率为２００Ｈｚ的带限信号ｆ（ｔ）采样，要使采样信号通过一理想定滤波器后能完全恢复
ｆ（ｔ），则（１）采样间隔Ｔ应满足何种条件？
（２）若以Ｔ＝１ｍｓ采样，理想低通滤波器的截止频率ｆｃ应满足什么条件？
考点３　调制与滤波
１．【南京航空航天大学，２０１１】
信号ｆ（ｔ）＝Ｓａ２（ω０ｔ）通过一个理想低通滤波器（其中Ｓａ（·）为抽样函数，ω０为实常数），如果信
号的幅度不产生失真则理想低通滤波器的幅频特性 Ｈ（ｊω） ＝ ；如果信号产生一个 ｔ０的延
迟，则理想低通滤波器的相频特性φ（ω）＝ 。
２．【北京邮电大学，２０１１】
已知某系统的幅频特性和相频特性分别为图（ａ）（ｂ）所示，则信号 ｓｉｎ（２ｔ）·ｓｉｎ（３ｔ）经过该系统
后是否产生失真？ 。
３．【上海交通大学】
已知一个系统的流程图如图所示。其输入为 ｘ（ｔ），第一步由 ｃｏｓ（５ωｔ）对其调制，得到 ｓ（ｔ），调
制后通过 Ｈ１（ω），输出为 ｐ（ｔ），然后 ｐ（ｔ）被 ｃｏｓ（３ωｔ）调制，得到 ｑ（ｔ），再通过 Ｈ２（ω），输出为
ｙ（ｔ）。已知Ｘ（ω）的频谱图案为三角波，从范围为 （－２ω，２ω），高度为１，Ｈ１（ω）是带通滤波器，通
频带（－５ω，－３ω）和 （３ω，５ω）高度为１。Ｈ２（ω）是低通滤波器，通频带 （－２ω，２ω），高度为 １。
要求：
（１）画出Ｓ（ω），Ｐ（ω），Ｑ（ω）；　（２）画出Ｙ（ω）
４．【西安电子科技大学】
系统的幅频特性 Ｈ（ｊω） 和相频特性如图（ａ）（ｂ）所示
则下列信号通过该系统时，不产生失真的是（　）
—２１—
（Ａ）ｆ（ｔ）＝ｃｏｓ（ｔ）＋ｃｏｓ（８ｔ） （Ｂ）ｆ（ｔ）＝ｓｉｎ（２ｔ）＋ｓｉｎ（４ｔ）
（Ｃ）ｆ（ｔ）＝ｓｉｎ（２ｔ）ｓｉｎ（４ｔ） （Ｄ）ｆ（ｔ）＝ｃｏｓ２（４ｔ）
５．【大连理工大学】
已知连续时间信号是一个实的周期信号，其傅里叶级数表达式为：
ｆ（ｔ）＝１＋０．５ｅｊ（ｔ＋２３π）＋ａｅ
－ｊｔ＋ｂｅｊ２ｔ＋０． 槡１２５２（１＋ｊ）ｅ－ｊ２ｔ－０．１５ｅｊ３ｔ＋ｃｅ－ｊ３ｔ＋ｄｅｊ４ｔ＋０．１ｅ－ｊ４ｅ－ｊ
１
６π
（１）试确定系数ａ，ｂ，ｃ，ｄ；
（２）若将该信号通过图所示的理想低通滤波器，求系统的输出信号
—３１—
郑君里《信号与系统》名校真题解析及典型题精讲精练
２．【电子科技大学】
已知一离散时间系统的输入和输出关系为
ｙ[ ]ｎ＝
１
４ ｘｎ－[ ]１＋２ｘ[ ]ｎ＋ｘｎ＋[ ]{ }１
求输入ｘ[ ]ｎ＝ｃｏｓ（π２ｎ）＋ｓｉｎ（πｎ）时的输出ｙ
[ ]ｎ。
３．【北京航空航天大学】
（１）下列信号中不是周期的 。
（Ａ）ｃｏｓ（ｎπ２）·ｃｏｓ（
ｎπ
４） （Ｂ）ｃｏｓ（ｎ８－π）
（Ｃ）ｓｉｎ（６π７＋１） （Ｄ）ｃｏｓ（ｎ
２π
８）
（２）设ｘ（ｎ）＝０，ｎ＜－２和ｎ＞４，试确定下列信号为零的ｎ值
①ｘ（ｎ－３）
（Ａ）ｎ＝３； （Ｂ）ｎ＜７； （Ｃ）ｎ＜７； （Ｄ）ｎ＜１和ｎ＞７
②ｘ（－ｎ－２）
（Ａ）ｎ＞０ （Ｂ）ｎ＞０和ｎ＜－６ （Ｃ）ｎ＝－２或ｎ＞０（Ｄ）ｎ＝－２
③ 一个ＬＴＩ系统输入 ｘ（ｎ）＝ａｎｕ（ｎ），单位样值响应 ｈ（ｎ）＝ｕ（ｎ）则 ｈ（ｎ）ｘ（ｎ）的结果
是 。
（Ａ）（１－ａ
ｎ）ｕ（ｎ）
１－ａ （Ｂ）（１－ａ
ｎ＋１）ｕ（ｎ）
１－ａ （Ｃ）１－ａ
ｎ
１－ａ （Ｄ）１－ａ
ｎ＋１
１－ａ
４．【浙江大学】
已知ｘ（ｎ）＝ｕ（ｎ）＋ｕ（ｎ－２），ｈ１（ｎ）＝δ（ｎ）－δ（ｎ－１）　ｈ２（ｎ）＝ａ
ｎｕ（ｎ－１）〗求ｙ（ｎ）＝
ｘ（ｎ）ｈ１（ｎ）ｈ２（ｎ）。
５．【西安电子科技大学】
已知线性时不变离散系统的单位脉冲响应 ｈ（ｎ）＝δ（ｎ）＋２δ（ｎ－１）＋３δ（ｎ－２），系统输入
ｇ（ｎ）＝３δ（ｎ）－２δ（ｎ－１）＋δ（ｎ－３），则系统零状态响应ｙｆ（ｎ）在ｎ＝２时的值，即ｙｆ（２）等于多少？
—０２—
第七章　离散时间系统的 ｚ域分析
【考情分析】
本章的考题主要涉及离散时间系统的ｚ域分析，也就是利用ｚ变换的性质求解系统，这些内容在
以往各高校研究生统考中出现频率较高，有部分题目稍微偏难。需要重点理解和掌握：
·ｚ变换以及反变换公式
·ｚ变换的性质以及收敛域判定
·利用ｚ变换求系统函数系统响应
·利用ｚ变换分析输出信号的幅频响应和相频响应
考点１　ｚ变换定义及性质
１．【东南大学】
（１）对线性移不变离散时间系统，下列说法中错误的是 （　）
（Ａ）极点均在Ｚ平面单位圆内的是稳定系统
（Ｂ）收敛域包括单位圆的是稳定系统
（Ｃ）收敛域是环状区域的系统是非因果系统
（Ｄ）单位函数响应单边的是因果系统
（２）已知某序列ｆ（ｋ）的双边ｚ变换及其收敛域为Ｆ（ｚ）＝－ ｚ
ｚ－１／３＋
ｚ
ｚ－１／４，
１
４ ＜ ｚ＜
１
３，则
原序列ｆ（ｋ）是（　）
（Ａ）－（３）ｋε（－ｋ－１）＋（１４）
ｋ
ε（ｋ） （Ｂ）－（１３）
ｋ
ε（－ｋ＋１）＋（１４）
ｋ
ε（ｋ）
（Ｃ）（１３）
ｋ
ε（ｋ）－（１４）
ｋ
ε（－ｋ－１） （Ｄ）（１３）
ｋ
ε（－ｋ－１）＋（１４）
ｋ
ε（ｋ）
（３）根据系统差分方程求响应时，线性移不变离散系统零输入
响应的标准定解条件 ｙｚｉ（０），ｙｚｉ（１），…ｙｚｉ（ｋ－１{ }） 是否是根据直接型框图所得系统状态变量的
初始状态（　）
（Ａ）ＦＩＲ系统 （Ｂ）全极点系统
（Ｃ）ＩＲ系统　 （Ｄ）都不是
２．【浙江大学】
求以下序列的ｚ变换，并标明其收敛域
（１）（１４）
ｎ
ｕ（ｎ）－（２３）
ｎ
ｕ（ｎ）
（２）－（１２）
ｎ
ｕ（－ｎ－１）
—１２—
郑君里《信号与系统》名校真题解析及典型题精讲精练
４．【西安电子科技大学】
离散序列ｆ（ｋ）＝∑
!
ｍ＝０
（－１）ｍδ（ｋ－ｍ）的ｚ变换及收敛域为
（Ａ） ｚ
ｚ－１，ｚ＜１
（Ｂ） ｚ
ｚ－１，ｚ＞１
（Ｃ） ｚ
ｚ＋１，ｚ＜１
（Ｄ） ｚ
ｚ＋１，ｚ＞１
５．【西安电子科技大学】
象函数Ｆ（ｚ）＝ ｚ２
（ｚ－１）（ｚ－２），１＜ ｚ＜２，则原序列ｆ（ｋ）＝
６．【北京交通大学】
选择题已知ｆ[ ]ｋ的ｚ变换Ｆ（ｚ）＝
１
（ｚ＋１２）（ｚ＋２）
，Ｆ（ｚ）的收敛域为（　）时，ｆ[ ]ｋ是因果序列。
（Ａ）ｚ＞
１
２ （Ｂ）ｚ＜
１
２ （Ｃ）ｚ＞２ （Ｄ）＜１２ ＜ ｚ＜２
考点２　系统函数和单位序列响应
１．【北京邮电大学，２０１１】
已知某线性离散时间因果系统框图如图所示。
（１）请写出描述该系统的差分方程
（２）求该系统的系统函数Ｈ（ｚ），并指明其收敛域
（３）求该系统的单位样值响应ｈ（ｎ）。
（４）写出该系统的频率响应表达式，并画出幅频谱图和相位频谱图
２．【哈尔滨工业大学】
已知某离散因果系统模拟框图如图所示，试求：
①系统函数
—２２—
—０３—