概要信息：

828 
华南理工大学 
2011 年攻读硕士学位研究生入学考试试卷 
（请在答题纸上做答，试卷上做答无效，试后本卷必须与答题纸一同交回） 
科目名称：电路原理 
适用专业：电机与电器；电力系统及其自动化；高电压与绝缘技术；电力电子与电力
传动；电工理论与新技术；电气工程(专业学位) 
本卷满分：150 分                                                 共 7 页 
第  1  页 
一． 填空题（本题共 60 分，每小题 5 分） 
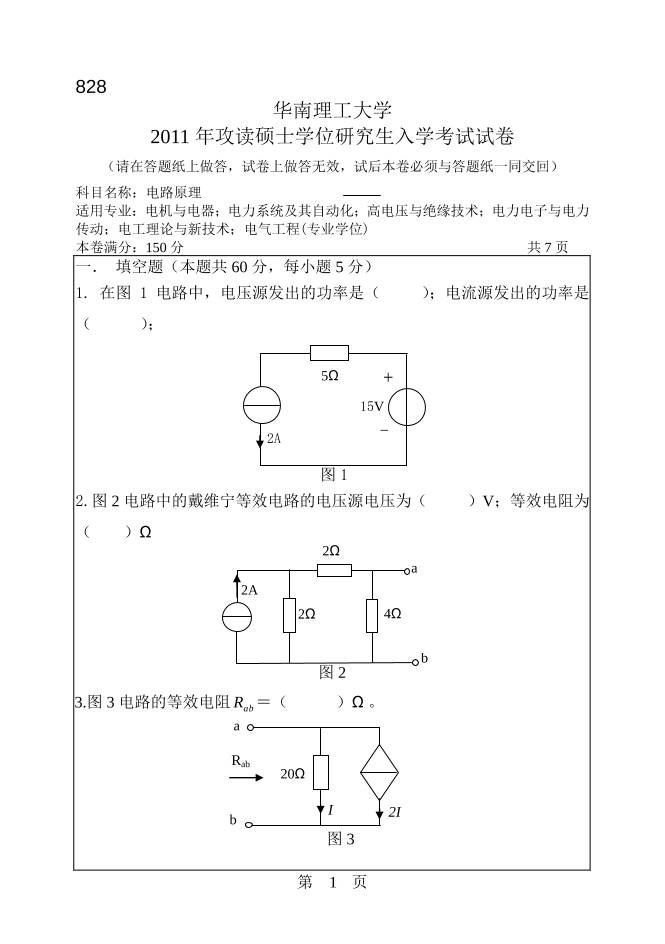
1. 在图 1 电路中，电压源发出的功率是（     ）；电流源发出的功率是
（      ）； 
     
 
 
 
 
 
图 1 
2.图 2 电路中的戴维宁等效电路的电压源电压为（     ）V；等效电阻为
（    ）Ω  
 
 
 
 
 
图 2 
3.图 3 电路的等效电阻 abR ＝（      ）Ω。 
 
 
 
 
 
图 3 
2A 
2Ω  
2Ω  
4Ω  
a 
b 
+ 
_ 
15V 
2A 
5Ω  
b 
a 
Rab 
2I 
20Ω  
I 
 
第  2  页 
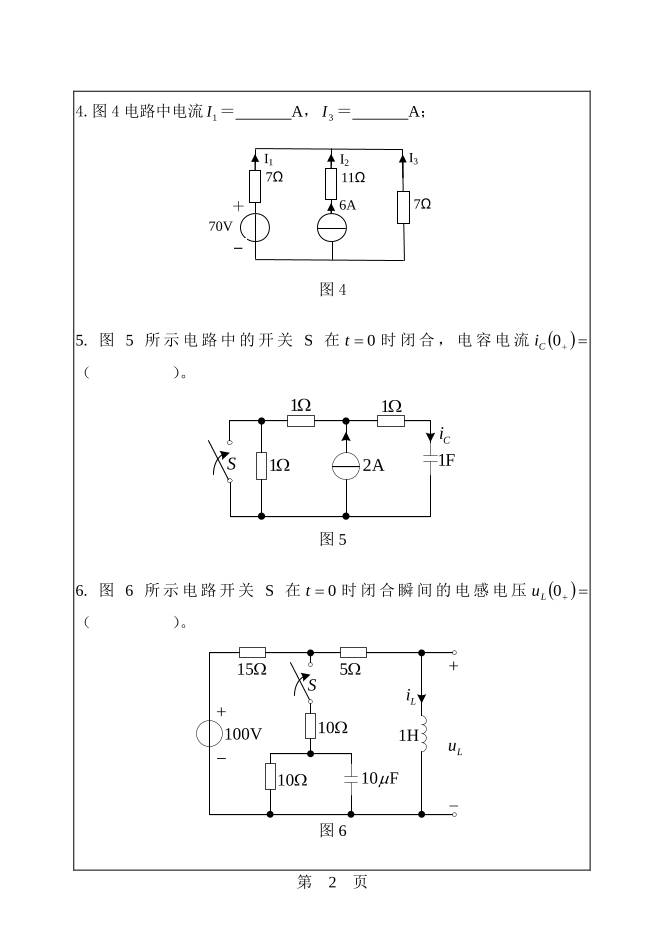
4.图 4电路中电流 1I ＝       A， 3I ＝       A； 
 
 
 
 
 
 
 
图 4 
 
5. 图 5 所示电路中的开关 S 在 0t 时闭合，电容电流   0Ci
（          ）。 
S 1
1 1
2A 1F
Ci
 
图 5 
 
6. 图 6 所示电路开关 S 在 0t 时闭合瞬间的电感电压   0Lu
（          ）。 
S


_
_
100V
15 5
10
10 10 F
1H
Li
Lu
 
图 6 
 
7Ω  
I1 
7Ω  
11Ω  
6A ＋ 
━ 
70V 
I2 I3 
 
第  3  页 
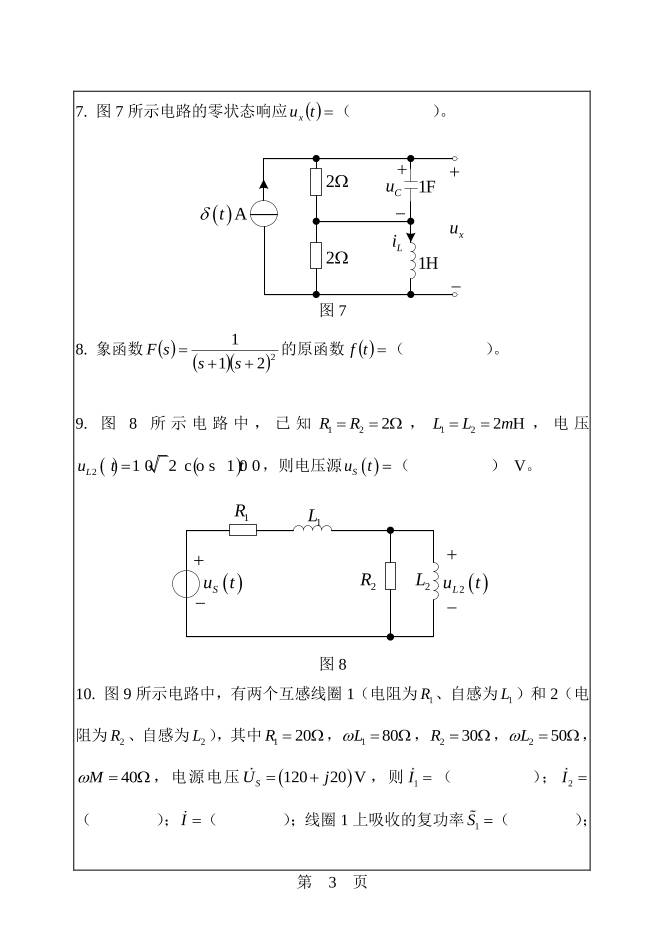
7. 图 7 所示电路的零状态响应   tux （          ）。 
 
 At
1F
1H
2
2
Li
Cu
xu
 


 
图 7 
8. 象函数  
  2
21
1


ss
sF 的原函数   tf （          ）。 
 
9. 图 8 所 示 电 路 中 ， 已 知 1 2 2R R   ， 1 2 2 HL L m  ， 电 压
   2 1 0 2 c o s 1 0 0 0  VLu t t ，则电压源  Su t （          ） V。 
 Su t  2Lu t
1R
2R
1L
2L
 
 
 
图 8 
10. 图 9 所示电路中，有两个互感线圈 1（电阻为 1R 、自感为 1L ）和 2（电
阻为 2R 、自感为 2L ），其中 1 20R  ， 1 80L  ， 2 30R  ， 2 50L  ，
40M  ，电源电压  120 20 VSU j  ，则 1I  （         ）； 2I 
（        ）； I （        ）；线圈 1 上吸收的复功率 1S （        ）；
 
第  4  页 
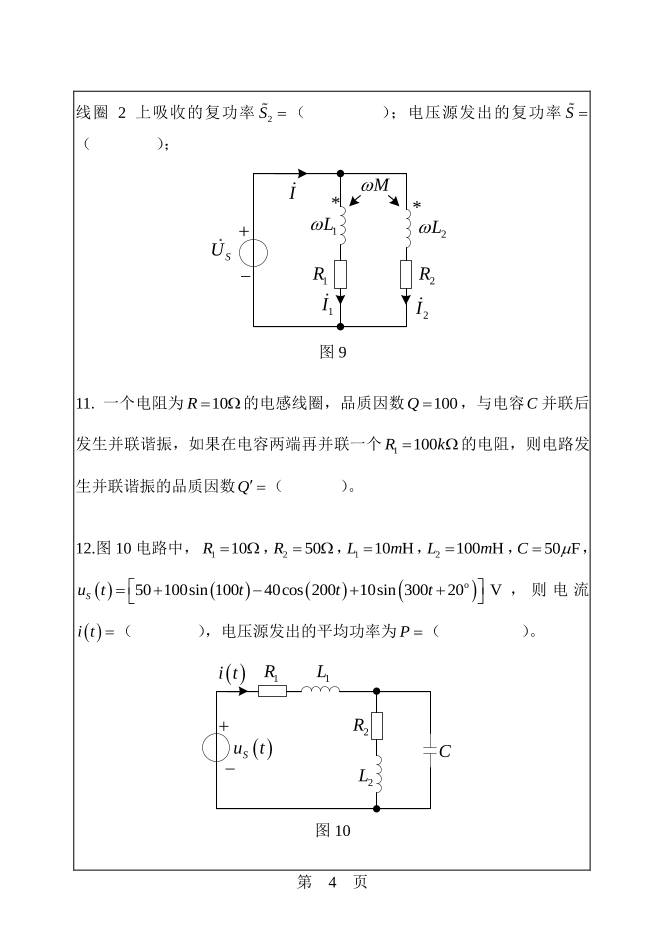
线圈 2 上吸收的复功率 2S （         ）；电压源发出的复功率 S 
（        ）； 
M
* *
1L
2L
1R 2R
SU


I
1I 2I
 
图 9 
 
11. 一个电阻为 10R  的电感线圈，品质因数 100Q  ，与电容C 并联后
发生并联谐振，如果在电容两端再并联一个 1 100R k 的电阻，则电路发
生并联谐振的品质因数Q （       ）。 
 
12.图 10 电路中， 1 10R  ， 2 50R  ， 1 10 HL m ， 2 100 HL m ， 50 FC  ， 
       o50 100sin 100 40cos 200 10sin 300 20  VSu t t t t     
 
， 则 电 流
 i t （        ），电压源发出的平均功率为P （          ）。 
 Su t
 i t 1R 1L
2R
2L
C


 
图 10 
 
 
第  5  页 
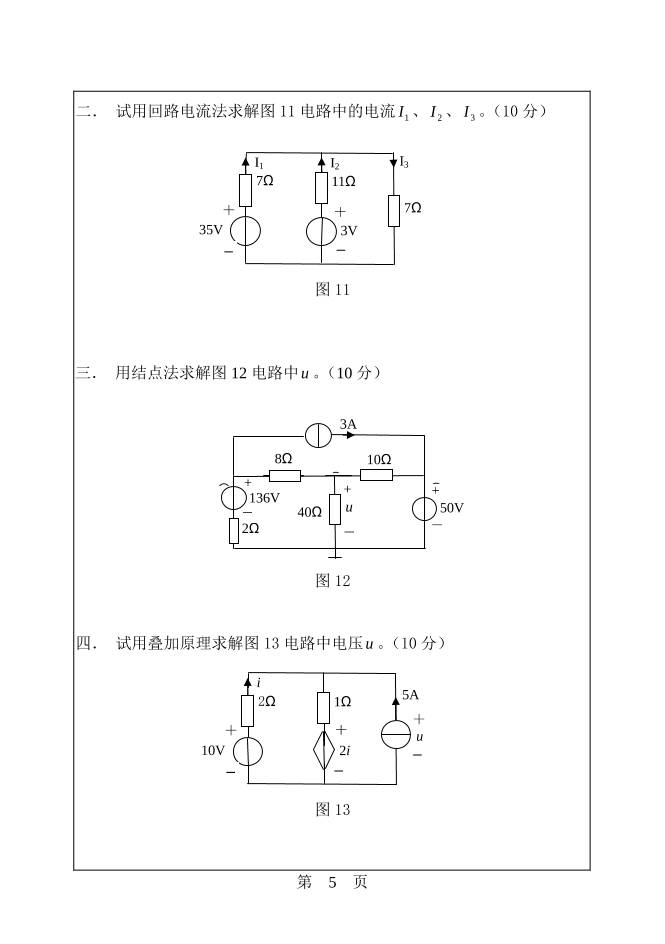
二． 试用回路电流法求解图 11电路中的电流 1I 、 2I 、 3I 。（10 分） 
 
 
 
 
 
 
 
图 11 
 
 
 
三． 用结点法求解图 12 电路中u 。（10 分） 
 
 
 
 
 
 
 
 
 
图 12 
 
 
四． 试用叠加原理求解图 13电路中电压u 。（10分） 
 
 
 
 
 
 
 
图 13 
 
 
7Ω  
I1 
7Ω  
11Ω  
3V 
＋ 
━ 
35V 
I2 I3 
＋ 
━ 
－ 
+ 
8Ω  
 
136V
VV 40Ω  u 
3A 
+ 
－ 
50V
VV 
10Ω  
 ② 
③ ① 
2Ω  
+ 
－ 
2Ω  
i 
u 
1Ω  
2i 
＋ 
━ 
10V 
5A 
＋ 
━ 
＋ 
━ 
 
第  6  页 
五．图 14 所示电路中，各参数均为已知，求电路的 ou 与 1su 、 2su 之间的关
系。（10 分） 




1su
2su
ou






1R 2R
3R 4R
 
图 14 
六． 图 15 所示电路中，开关 S 在 0t 时闭合，求 0t 时的电压  tu 。（10
分） 
S
80V




i
5i
2
1
1
5H
 u t
 
图 15 
七． 图 16 电路中开关 S 在 0t 时断开，试用拉普拉斯变换法求 0t 时的
电容电流  tiC 。（10 分） 
S
1H
*
*
1H
3H
3A
1
1
11F
 Ci t
 
图 16 
 
第  7  页 
八．图 17 所示电路中，已知电压源电压为    V 601000cos2200 o ttuS  ，
电压表 V1 和 V2 的读数都为 200V， H 4.01 L ， F 5C ，试求电流  ti 、
 ti1 、  ti2 ，电阻 R 、电感
2L 及电压源发出的平均功率 P 。（15 分） 
 su t
1V
2V
1L
2L
R
C
 1i t  2i t
 i t


 
图 17 
 
九． 线电压为 380V 的三相对称电源供电给两组对称负载，如图 18 所示，
已知 o380 30  VABU   ，  1 12 16Z j  ，  2 48 36Z j  ，线路阻抗
 1 2lZ j  。试求：（1）各负载的相电流 1AI 、 1BI 、 1CI 、 2AI 、 2BI 、 2CI ；
（2）线路中的电流 AI 、 BI 、 CI ；（3）两组负载分别消耗的功率 1P 、 2P ；
（4）三相电源发出的功率 P 。（15 分） 
AI
BI
CI
1AI
1BI
1CI
2AI
2BI
2CI
lZ
lZ
lZ
1Z
1Z
1Z
2Z 2Z
2Z
ABU


A
B
C
 
图 18