概要信息：

测题自 10（内 E） 
题  号 一 二 三 四 五 六 七 八 九 十 总     分 
得  分            
一、填空题（共 10 空，每空 2 分，共 20 分） 
答题须知：本题答案必须写在如下表格中，否则不给分。 
小题号 1 2 3 4 5 6 7 8 9 10 
答案           
1． 设 A 和 B 是两个随机事件。试表示以下事件：          
A 和 B 中至少有一个发生__________；A 发生但 B 不发生______________。 
2． 设 A 与 B 是互斥的两个随机事件，已知 P(A)=0.2，P(B)=0.7。则 
 P(A∪B)= _____________   ________；P(AB)=___________ _ __  _________。 
3． 设 A 和 B 相互独立的两个随机事件，已知 P(A)=0.4，P(B)=0.2，则 
P(A|B)=____________    __________；P(A－B)=___________   ___________。 
4． 设随机变量 X 的数学期望 E(X)=3，方差 D(X)=4。则   
E(2X+3)=__________ __     ________；D(2X－3)=____________ ___________。 
5． 设随机变量 X 服从标准正态分布，已知 P(X<0.5)=0.69。则 
P(|X|<0.5)=_________   ___________；P(X<−0.5)=_______ __   ___________。 
 
二、单选题（共 10 小题，每小题 2 分，共 20 分） 
答题须知：本题答案必须写在如下表格中，否则不给分。 
小题号 1 2 3 4 5 6 7 8 9 10 
第 1 页 共 7 页 
自测题 （内 ） 10 E
第 2 页 共 7 页 
答案           
1. A 与 B 是两个随机事件，若 AB=φ，则称这两个随机事件是（     ）。 
(A) 对立；   (B) 独立；   (C)互斥；   (D) 相容。 
2. 函数 sin x 在以下哪个区间上可以作为随机变量的密度函数？(       ) 
 (A) 0
2
π⎡ ⎤
⎢⎣ ⎦
, ⎥；  (B) [ ]0 π, ；   (C) 
30
2
π⎡ ⎤
⎢ ⎥⎣ ⎦
, ；  (D) [ ]0 2π, . 
3. 设 F(x)是随机变量 X 的分布函数，则 F(x)具有性质(       )。 
 x x x x
x x x x
A F x 1 F x 0 B F x 0 F x 1
C F x 0 F x 0 D F x F x
→−∞ →+∞ →−∞ →+∞
→−∞ →+∞ →−∞ →+∞
= = =
= = = −∞
( ) lim ( ) , lim ( ) , ( ) lim ( ) , lim ( ) ,
( ) lim ( ) , lim ( ) , ( ) lim ( ) , lim ( ) .
=
= +∞
 
4. 设随机变量 X 服从正态分布 N(4, 9)，则（    ）。 
(A) E(X)=3，D(X)=4；(B) E(X)=9，D(X)=4；(C) E(X)=4，D(X)=3；(D) E(X)=4，D(X)=9。 
5. 设 1 2 3 是总体 X 的随机样本，则下列那些样本函数不是统计量（     ）。 X ,X ,X
(A)
3
i
k 1
1 X
3 =
∑ ；  (B) ；  (C) 1X (
3
2
i
i 1
1 X
3 =
)− θ∑ ； (D)  1 2X Xmax{ , }
6. 设 是总体 N(2,25)的随机样本,则样本均值1 2 5X ,X ,...,X X 服从的分布是（    ）。 
(A) N(2, 5)；      (B) N(2, 25)；     (C) N(2/5,5)；     (D)N(2/5, 25) 
7. 设 是总体 N(μ,σ2)的随机样本,则服从 t(4)分布的样本函数是（    ） 1 2 5X ,X ,...,X
(A)
X
5
− μ
σ
( )
；  (B)
X
4
− μ
σ
( )
；  (C)
X
s 5
− μ( )
；  (D)
X
s 4
− μ( )
 
8. 概率论中论证大量测量值的算术平均值具有稳定性的定理被称为（   ）。 
 (A) 概率公理化定义；      (B)大数定律；  
 (C) 小概率事件实际不可能性原理；   (D)中心极限定理。 
9. 设 θ̂ 是总体参数θ 的点估计量。若E θ = θˆ( ) ，则称 θ̂ 是θ 的(        )估计量。 
 (A)相合；   (B)一致；   (C)有效；   (D)无偏 
10. 在假设检验中，原假设不成立但被接受，这种错误称为第(         )类错误。 
 (A) 一；    (B) 二；    (C) 三；    (D) 四 
三、计算题（共 8 小题，每小题 5 分，共 40 分） 
自测题 （内 ） 10 E
第 3 页 共 7 页 
1. 一箱中装有 4 个红球和 6 个黑球，随机取 3 个球，求其中（恰）有 1 个黑球的概率。 
 
2. 一条生产线次品率为 10%，求随机抽取 5 件中至多有 1 件次品的概率。 
 
3. 若鸡蛋的孵化率为 80%，则 10000 个鸡蛋中不足 7000 个孵化的概率是多少？. 
4. 已知随机变量 X 的密度函数为 ，求常数 a 和 EX. 
ax, 0
θ ⎨
⎩ 其它
, 其中θ>0. x1,x2,…,xn是 X 的一个随机样
本,求参数θ的最大似然估计。 
 
8.设(X,Y)是二维离散随机变量，其联合分布律如下表 
X             Y －1 0 1 
1 0.2 0.3 0.1 
2 0.1 0.1 0.2 
求 X 的边缘分布和当 Y=1 时 X 的条件分布，并判断 X 与 Y 是否相互独立。 
 
四、应用题(共 3 小题，每小题 5 分，共 15 分) 
 
1．商场销售的灯泡由由 A 与 B 两家工厂生产。A 厂的产品占总产量的 70%，B 厂的产品占总
产量的 30%。已知 A 厂产品的次品率为 5%，B 厂产品的次品率为 10%。已若随机抽取一个灯
泡是次品，求其是 A 厂生产的概率。 
 
2．面粉厂规定每袋面粉标准重量为 10kg。从已装好的面粉中随机抽查 9 袋，测得样本平均重
量为 10.5kg。假定袋装面粉重量服从正态分布 N(μ，0.25)。检验该厂面粉袋装重量是否符合标
准(显著水平α = 0.1，检验临界值查卷尾表 1 和表 2)。 
  
3.选取两个品牌灯泡各 9 只进行使用寿命测试。测试结果统计如下表  
指标 品牌 1 品牌 2 
样本均值(小时) 2000 1970 
标准差(小时) 100 80 
假设两品牌的灯泡寿命均服从正态分布且方差相同。试检验两品牌灯泡寿命有无显著差异？(显
著水平α = 0.01，检验临界值查卷尾表 1 和表 2) 
 
五、证明题(第 1 小题 3 分，第 2 小题 2 分，共 5 分)  
自测题 （内 ） 10 E
第 4 页 共 7 页 
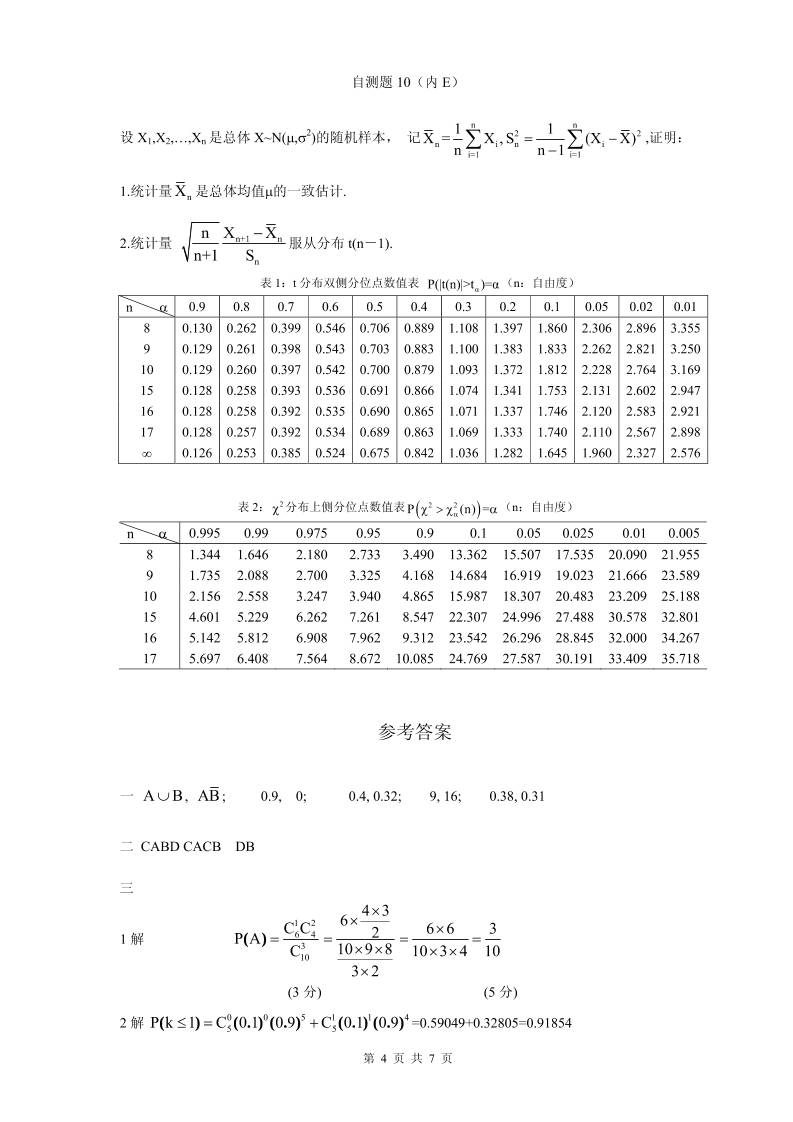
设 X1,X2,…,Xn 是总体 X~N(μ,σ2)的随机样本， 记
n n
2 2
n i n i
i=1 i=1
1 1X = X , S (X X)
n n 1
=
−∑ ∑ − ,证明： 
1.统计量 nX 是总体均值μ的一致估计. 
2.统计量 n+1 n
n
X Xn
n+1 S
−
服从分布 t(n－1). 
表 1：t 分布双侧分位点数值表 （n：自由度） αP(|t(n)|>t )=α
n    α 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0.05 0.02 0.01
8 0.130  0.262  0.399  0.546 0.706 0.889 1.108 1.397 1.860  2.306  2.896 3.355 
9 0.129  0.261  0.398  0.543 0.703 0.883 1.100 1.383 1.833  2.262  2.821 3.250 
10 0.129  0.260  0.397  0.542 0.700 0.879 1.093 1.372 1.812  2.228  2.764 3.169 
15 0.128  0.258  0.393  0.536 0.691 0.866 1.074 1.341 1.753  2.131  2.602 2.947 
16 0.128  0.258  0.392  0.535 0.690 0.865 1.071 1.337 1.746  2.120  2.583 2.921 
17 0.128  0.257  0.392  0.534 0.689 0.863 1.069 1.333 1.740  2.110  2.567 2.898 
∞ 0.126  0.253  0.385  0.524 0.675 0.842 1.036 1.282 1.645  1.960  2.327 2.576 
 
表 2： 分布上侧分位点数值表2χ ( )2 2P (n)α =χ > χ α （n：自由度） 
n       α  0.995 0.99 0.975 0.95 0.9 0.1 0.05 0.025 0.01 0.005
8 1.344  1.646  2.180 2.733 3.490 13.362 15.507 17.535  20.090  21.955 
9 1.735  2.088  2.700 3.325 4.168 14.684 16.919 19.023  21.666  23.589 
10 2.156  2.558  3.247 3.940 4.865 15.987 18.307 20.483  23.209  25.188 
15 4.601  5.229  6.262 7.261 8.547 22.307 24.996 27.488  30.578  32.801 
16 5.142  5.812  6.908 7.962 9.312 23.542 26.296 28.845  32.000  34.267 
17 5.697  6.408  7.564 8.672 10.085 24.769 27.587 30.191  33.409  35.718 
 
 
  参考答案 
 
一 , A B∪ AB ;     0.9,  0;      0.4, 0.32;    9, 16;    0.38, 0.31 
 
二 CABD CACB  DB 
 
三 
1 解    
1 2
6 4
3
10
C CP A
C
=( )
4 36
2
10 9 8
3 2
×
×
=
× ×
×
6 6 3
10 3 4 10
×
= =
× ×
 
      (3 分)      (5 分) 
2 解 =0.59049+0.32805=0.91854 0 0 5 1 1
5 5P k 1 C 0 1 0 9 C 0 1 0 9≤ = +( ) ( . ) ( . ) ( . ) ( . )4
自测题 （内 ） 10 E
第 5 页 共 7 页 
      (3 分)      (5 分) 
 
3 解： X~B(10000,0.8) 
X 10000 0 8 7000 10000 0 8P X 7000 P
10000 0 8 0 2 10000 0 8 0 2
− × − ×⎧ ⎫
≤ = ≤⎨ ⎬
× × × ×⎩ ⎭
. .{ }
. . . . 0 25 0= − ≈( )Φ    
        (3 分)      (5 分) 
4 解： 
2 22
00
a 11 f x dx axdx x a
2 2
∞
−∞
= = =∫ ∫( ) , =      (3 分)   
 
2 23
00
1 1EX xf x dx x xdx x
2 6 3
∞
−∞
= = ⋅ =∫ ∫( ) 4
=      (5 分) 
 
5 解：因为  (1 分)  262.6)15(,488.27)15(,131.2)15(t,05.0 2
975.0
2
025.005.0 ==== χχα
所以均值的置信区间为: 
0 1 0 11 2 131 1 2 131
16 16
⎡ ⎤
− +⎢
⎣ ⎦
. .. , . ⎥             (3 分)  
方差的置信区间为: 
2 215 0 1 15 0 1
27 488 6 262
⎡ ⎤× ×
⎢
⎣ ⎦
( . ) ( . ),
. . ⎥           (5 分) 
6  解：  3
YF y P Y y P 1 X y= ≤ = − ≤( ) { } { }        (1 分)  
3P X 1 y 1 F 1 y= ≥ − = − −{ ( ) } (( )3 )
2
     (3 分)  
3 3
Y Yf y F y 1 F 1 y f 1 y 3 1 y′ ′= = − − = − − − −( ) ( ) [ (( ) )] (( ) )[ ( ) ]    
2
6
3 1 y x
1 1 y
−
= −∞ <
π + −
( ) (
( ( ) )
< +∞)       (5 分) 
7 解：   (2 分) 
         (3 分) 
  
1n n
1 n n
1 2 n i i i
i 1 i 1
L x x x 3 x 3 x x 3
− θ+
θ − θ+ θ
= =
⎛ ⎞
θ = θ = θ >⎜ ⎟
⎝ ⎠
∏ ∏
( )
( )( , , ..., ; )
n
i
i 1
L n n 3 1 x
=
θ = θ + θ − θ + ∑ln ( ) ln ln ( ) ln
n
i
i 1
d L n n 3 x 0
d =
= + − =
θ θ ∑ln ln ln          (4 分) 
  n n
i i
i 1 i 1
n 1
1x n 3 x 3
n= =
θ = =
− −∑ ∑
ˆ
ln ln ln ln
        (5 分) 
8  解 
Y 1 2         (1 分) 
自测题 （内 ） 10 E
第 6 页 共 7 页 
PY 0.6 0.4 
 
X －1 0 1 
PX 0.3 0.4 0.3 
  (2 分) 
 
X －1 0 1 
PX|Y=1 1/3 1/2 1/6 
  (3 分) 
因为P X 1 P X 1 Y 1= ≠ = =( ) ( | ) ，所以 X 与 Y 不相互独立。     (5 分) 
 
四 
1 解：令 D 表示次品，A 表示产品由 A 生产，B 表示产品由 B 生产。 
  
P A P D AP A D
P D
=
( ) ( | )( | )
( )
 
0 7 0 05 0 035 7
0 7 0 05 0 3 0 1 0 065 13
×
= = =
× + ×
. . .
. . . . .
 
               (2 分)               (4 分)                (5 分) 
 
2. 解：假设  0 1H 10 H 10μ = μ: , : ≠          (1 分) 
检验统计量     0XU N
n
− μ
=
σ
~ ( , )
/
0 1         (2 分) 
检验临界值              (3 分) 0 1u u 1 645α = =. .
检验统计量样本值   0X 10 5 10U
n 0 5 9
− μ −
= =
σ
.
/ . /
3=
2
       (4 分) 
统计推断  因为 |U|=3>1.645，所以拒绝原假设，即在 0.1 显著水平上认为该面粉厂袋装面粉不
符合 10kg 的标准。              (5 分) 
3. 解：假设              (1 分) 0 1 2 1 1H Hμ = μ μ ≠ μ: , :
检验统计量     1 2
1 2
w
1 2
X XT t n
1 1S
n n
−
=
+
~ ( )n 2+ −
1.
         (2 分) 
检验临界值              (3 分) 1 2 0 01t n n 2 t 16 2 92α + − = =.( ) ( )
检验统计量样本值   1 2
2 2
w
1 2
X X 2000 1970T 0 703
1 1 8 100 8 80 1 1S
n n 16 9 9
− −
= = =
× + ×+ +
.  (4 分) 
统计推断  因为 |T|=0.707<2.921，所以接受原假设，即在 0.01 显著水平上认为两品牌灯泡寿命
无显著差异。                 (5 分) 
 
五 
自测题 10（内 E） 
第 7 页 共 7 页 
1 证：因为
2
nEX DX
n
σ
= μ =, ，由切比谢夫不等式有 { }
2
2P X 1
n
σ
− μ < ε > −
ε
| |   (1 分) 
所以  { }
2
2n n
1 P X 1
n→∞ →∞
⎛ ⎞σ
≥ − μ < ε > −⎜ ⎟ε⎝ ⎠
lim | | lim 1= ，即有  { }
n
P X 1
→∞
− μ < ε =lim | |   
由定义知X 是总体均值μ的无偏估计和一致估计。      (3 分) 
2. 证：因为 
2
2 n
n+1 n 2
(n 1)S1+nX X ~ (0, ), ~ (n 1
n σ
N − 2 )− σ χ −       (1 分) 
所以   
n+1 n
n+1 n
2
n n
2
n+1(X X )X Xn n ~ t(n 1)
n+1 S (n 1)S (n 1)
− σ−
= −
−
−
σ
       (1 分)