概要信息：

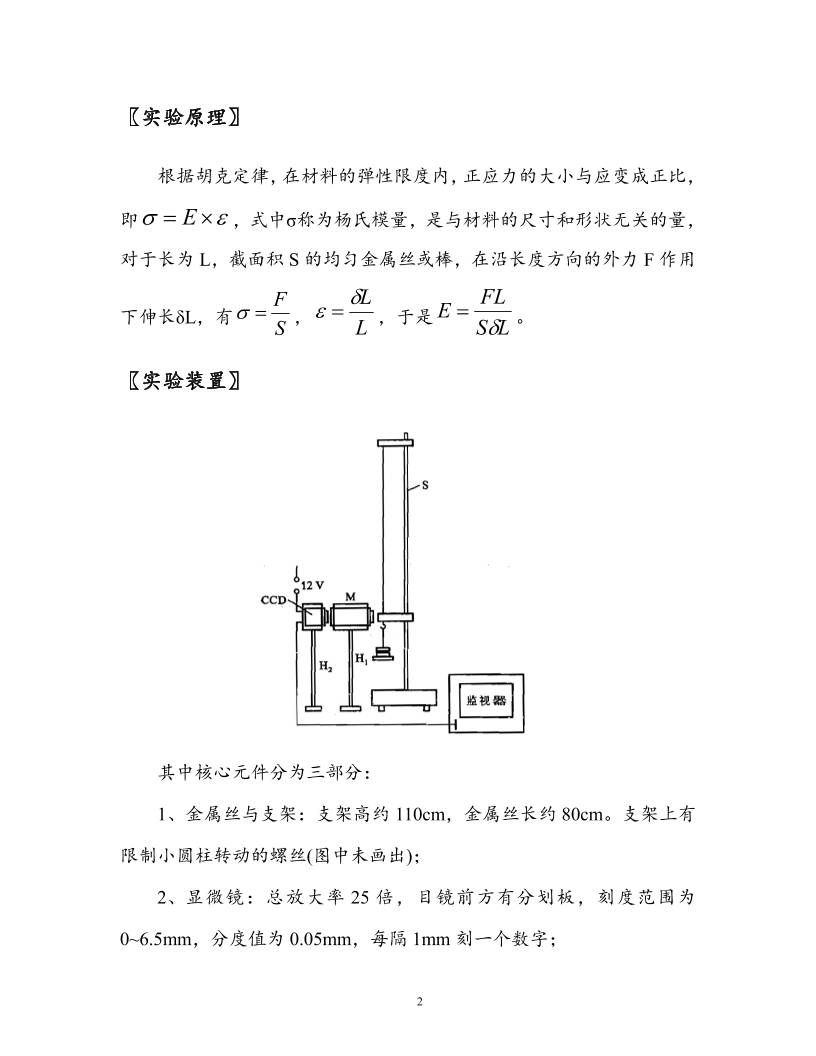
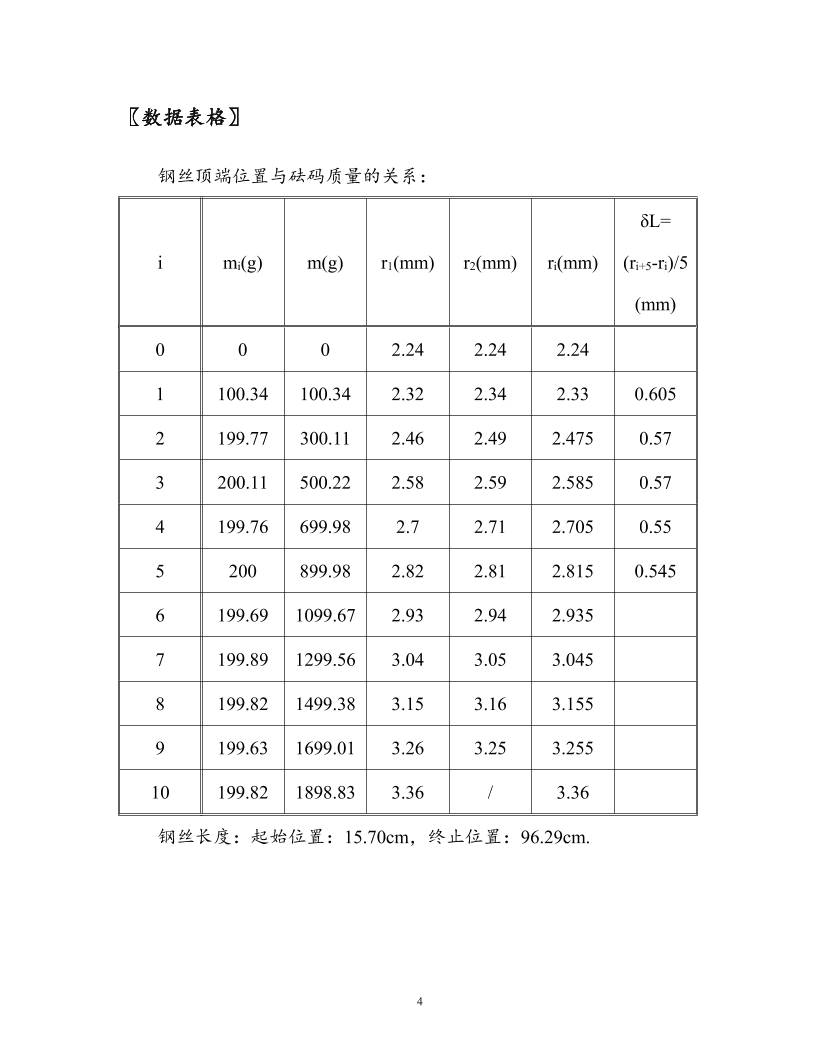
1
〖实验八〗
测定金属的杨氏模量
实验时间 2015年 3月 17日
报告时间 2015年 3月 18日
祁周 1300011454
周二下午第 2组 3号
一、CCD成像系统测定杨氏模量
〖目的要求〗
1、用金属丝的伸长测量杨氏模量；
2、用 CCD成像系统测量微小长度变化；
3、用逐差法，作图法和最小二乘法处理数据。
〖仪器用具〗
杨氏模量专用支架，显微镜，CCD成像系统(CCD摄像机、监视器)，
带卡口的米尺(精度 1mm)，螺旋测微器(精度 0.001mm)，电子天平
(JA21002，2100g，10mg)，砝码(约 200g/个)若干。
2
〖实验原理〗
根据胡克定律，在材料的弹性限度内，正应力的大小与应变成正比，
即   E ，式中σ称为杨氏模量，是与材料的尺寸和形状无关的量，
对于长为 L，截面积 S的均匀金属丝或棒，在沿长度方向的外力 F作用
下伸长δL，有 S
F
 ， L
L  ，于是 LS
FLE

 。
〖实验装置〗
其中核心元件分为三部分：
1、金属丝与支架：支架高约 110cm，金属丝长约 80cm。支架上有
限制小圆柱转动的螺丝(图中未画出)；
2、显微镜：总放大率 25 倍，目镜前方有分划板，刻度范围为
0~6.5mm，分度值为 0.05mm，每隔 1mm刻一个数字；
3
3、CCD成像显示系统。
〖实验内容〗
1、调节仪器
调节支架铅直，使金属丝下端的小圆柱与平台无摩擦移动。然后调
整显微镜目镜，分划板成像清晰。再调节物镜的位置，将小圆柱上的刻
线清晰无视差地成在分划板上。装好 CCD，将镜头对准目镜，调整光圈
直至监视器上看到清晰的图像。
2、观测金属丝受外力拉伸后的伸长变化
用电子天平校准砝码，记录好砝码顺序。依次加砝码，记录数据；
再将其逐个减去，记录对应数据。
3、测量金属丝长度与直径
金属丝长度用米尺测量一次，直径用螺旋测微器测量 10次。
4、注意事项
⑴CCD不可正对强光。不要使 CCD视频输出短路。前表面禁止用
手触摸。
⑵保持金属丝平直，测量时切勿扭折。
4
〖数据表格〗
钢丝顶端位置与砝码质量的关系：
i mi(g) m(g) r1(mm) r2(mm) ri(mm)
δL=
(ri+5-ri)/5
(mm)
0 0 0 2.24 2.24 2.24
1 100.34 100.34 2.32 2.34 2.33 0.605
2 199.77 300.11 2.46 2.49 2.475 0.57
3 200.11 500.22 2.58 2.59 2.585 0.57
4 199.76 699.98 2.7 2.71 2.705 0.55
5 200 899.98 2.82 2.81 2.815 0.545
6 199.69 1099.67 2.93 2.94 2.935
7 199.89 1299.56 3.04 3.05 3.045
8 199.82 1499.38 3.15 3.16 3.155
9 199.63 1699.01 3.26 3.25 3.255
10 199.82 1898.83 3.36 / 3.36
钢丝长度：起始位置：15.70cm，终止位置：96.29cm.
5
测量钢丝直径 D(mm)：千分尺零点读数：0.001mm
0.325 0.323 0.321 0.325 0.329 0.322
0.321 0.322 0.325 0.324 0.326 0.325
均值：0.324mm，D=0.324-0.001=0.323mm
〖数据处理及结果〗
1、逐差法处理数据
首先求出每增加 5个砝码的长度平均变化量：
δL=(ri+5-ri)/5(mm) 0.121 0.114 0.114 0.11 0.109
δL均值：0.1136mm，标准值的标准差σ：0.002mm，精度 e：0.01mm，
不确定度： mme 006.0
3
2
2 




 ，所以δL=(0.114±0.006)mm
钢丝直径 d：均值为 0.3230mm，标准值的标准差σ：0.00067mm，
精度 e： 0.004mm，不确定度： mme 002.0
3
2
2 




 ，所以
d=(0.323±0.002)mm
砝码质量 m：均值为 199.8322g，标准值的标准差σ：0.04988g，精
度 e：0.01g，不确定度： g05.0
3
2
2 





e ，所以 m=(199.83±0.05)g.
6
钢丝长度 L=96.29-15.70=80.59cm，e=0.1cm，所以 L=(80.59±0.06)cm
取 g=9.801m/s2.
2
11
2
11
2222
2
11
2
10)02.070.1(
1002.0
%387.12
1069566.14
m
NE
m
NE
L
L
d
d
L
L
m
m
E
E
m
N
Ld
mgLE




























2、作图法和最小二乘法处理数据
7
斜率
值 5.68×10-4
标准差 0.07×10-4
回归系数 值 0.9992
2
11
2
11
222
2
11
2
4-
2
10)03.070.1(
1003.0
%749.12
106971.1
d
4Lg
10×0.07)(5.68
d
4Lgk
m
NE
m
NE
k
k
d
d
L
L
E
E
m
N
k
E
E
























〖讨论及思考〗
我们采用了两种手段来进行数据处理，效果基本是相同的，它们的
不确定位是一样的，所以我们可以认为两种方法在这一问题中的精确程
度基本相同。
二、梁的弯曲测定杨氏模量
〖目的要求〗
1、用梁的弹性弯曲测定金属材料的杨氏模量；
2、用读数显微镜测量微小长度的变化；
8
〖仪器用具〗
可移动的平行刀口及基座，金属梁，砝码及悬砝码的框架，读数显
微镜，米尺，游标卡尺，螺旋测微器。
〖实验原理〗
在梁的弹性限度内，不计梁自身的重力，梁中点的挠度λ，在λ远小
于 l时，有 3
3
4 ah
GlE

 。
其中 l为两刀口距离，a为梁的宽度，h为梁的厚度，G=mg，m为
悬挂砝码的质量。
实验装置如图所示
9
〖实验内容〗—测定梁样品材料的杨氏模量
如图搭好设备，并调好读数显微镜使金属框刀口的像清晰，然后读
出梁边缘位置。在砝码盘上顺序地加砝码，每次下降显微镜读出梁原来
边缘的位置。注意螺距差的问题。然后再反向做一次。最后测出梁的有
效长度，宽度和厚度。用作图法和逐差法计算杨氏模量。
〖数据表格〗
刀口位置与砝码质量的关系：
i mi(g) m(g) r1(mm) r2(mm) ri(mm)
0 100.34 100.34 30.591 30.497 30.5440
1 199.77 300.11 29.472 29.372 29.4220
2 200.11 500.22 28.230 28.265 28.2475
3 199.76 699.98 27.136 27.114 27.1250
4 200.00 899.98 25.981 25.979 25.9800
5 199.69 1099.67 24.852 24.848 24.8500
6 199.89 1299.56 23.629 23.762 23.6955
梁的宽度 a(mm)：（使用千分尺测量）
9.909 9.870 9.860 9.860
9.829 9.828 9.841 9.822
10
刀口距离 L：起始位置 2.96cm，终止位置 28.70cm。
梁的厚度 h(mm)：（使用千分尺测量）
1.541 1.549 1.556
1.542 1.557 1.565
〖数据处理及结果〗
斜率
值 -0.00571
标准差 0.00001
回归系数 值 0.99999
梁的宽度 a：均值为 9.85238mm,标准值的标准差σ:0.01mm，精度 e：
0.004mm，不确定度： mme 01.0
3
2
2 




 ，所以 a=(9.85±0.01)mm.
11
梁的厚度 h：均值为 1.5517mm,标准值的标准差σ：0.004mm,精度
e:0.004mm,不确定度： mme 005.0
3
2
2 




 ,所以m=(1.552±0.005)mm.
刀口距离 L=28.70-2.96=25.74cm，e=0.1cm，所以 L=(25.74±0.06)cm.
取 g=9.801m/s2.
2
11
2
11
2222
2
11
3
3
3
3
10)02.099.1(
1002.0
%2100.133
10987011.1
4
00001.000571.0
4
m
NE
m
NE
h
h
a
a
k
k
L
L
E
E
m
N
kah
gLE
Eah
gLk



























〖讨论及思考〗
⑴支柱之间相距不能太近，砝码不能过重，金属框刀口要尽量位于
梁的中间；
⑵用叉丝的交点对准中间刀口的尖端比较好，这样可以保证每次测
量的都是同一位置的λ；
⑶测 a、h用螺旋测微器，测 l用米尺，这是在估计了被测长度的量
级以后，为了使相对不确定度大致在同一量级的考虑，因为合成后的相
12
对不确定度基本由具有最高量级不确定度的因子所决定。想测准 l，要
尽量保证端面与测量尺的端面对齐，此外可以多次测量减小误差。