概要信息：

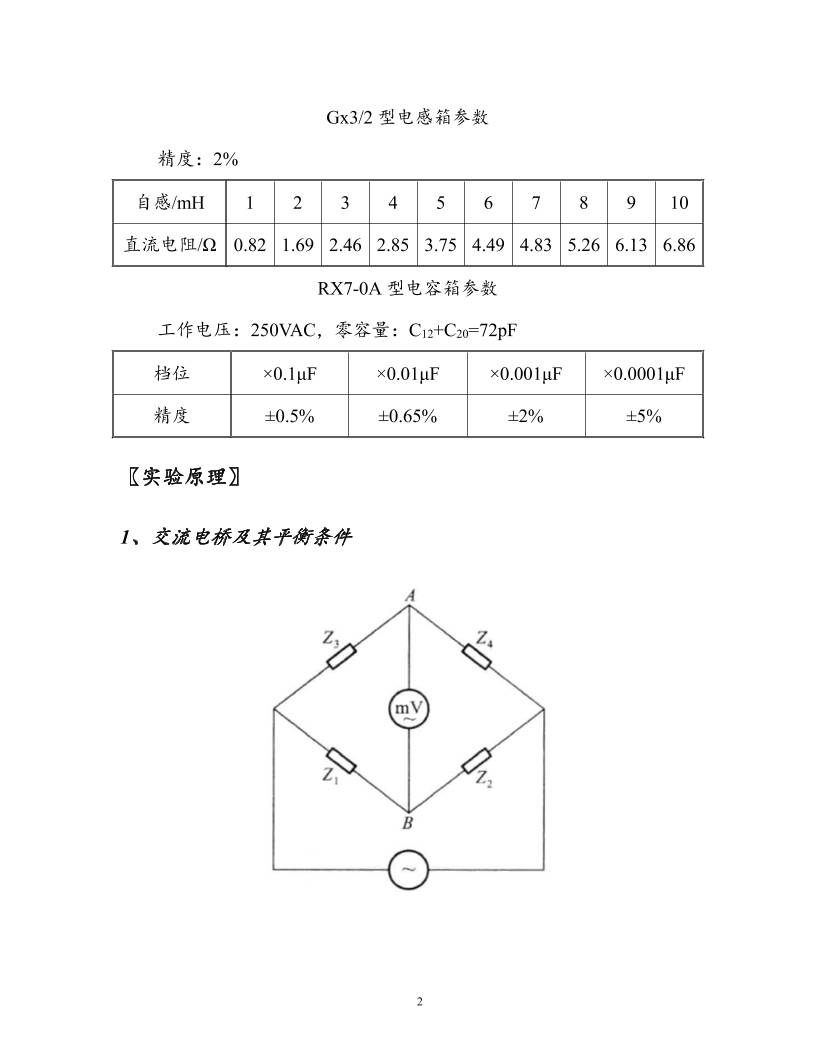
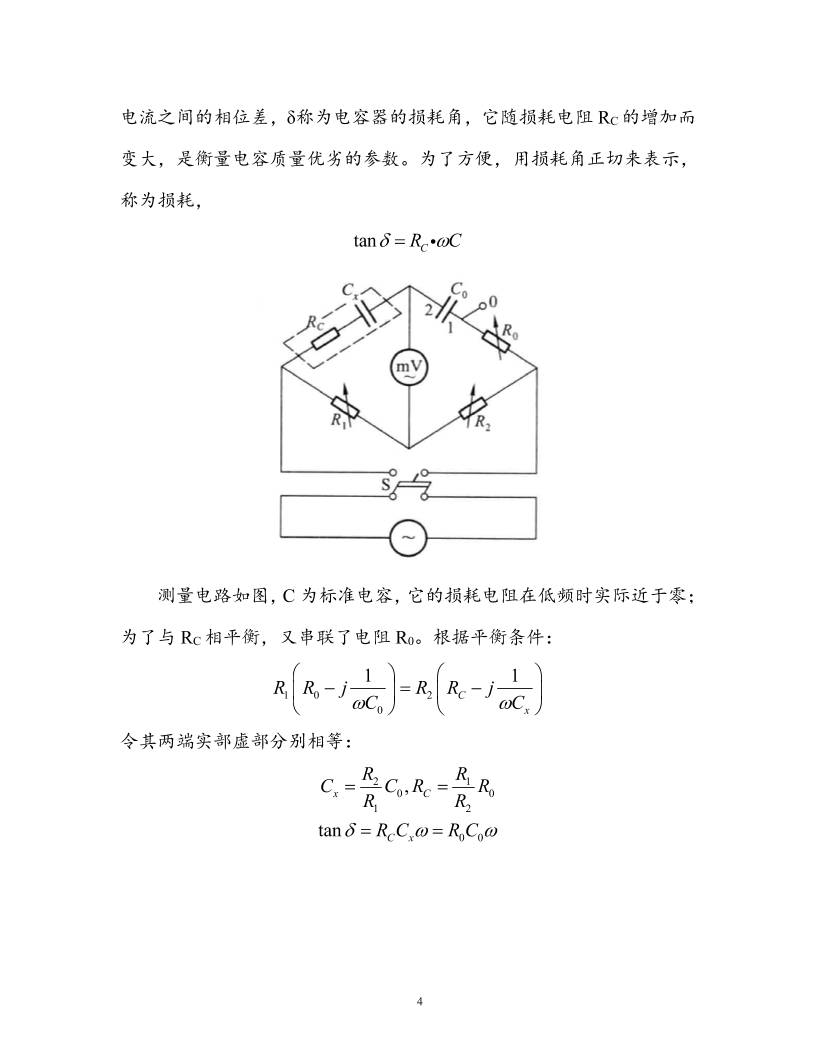
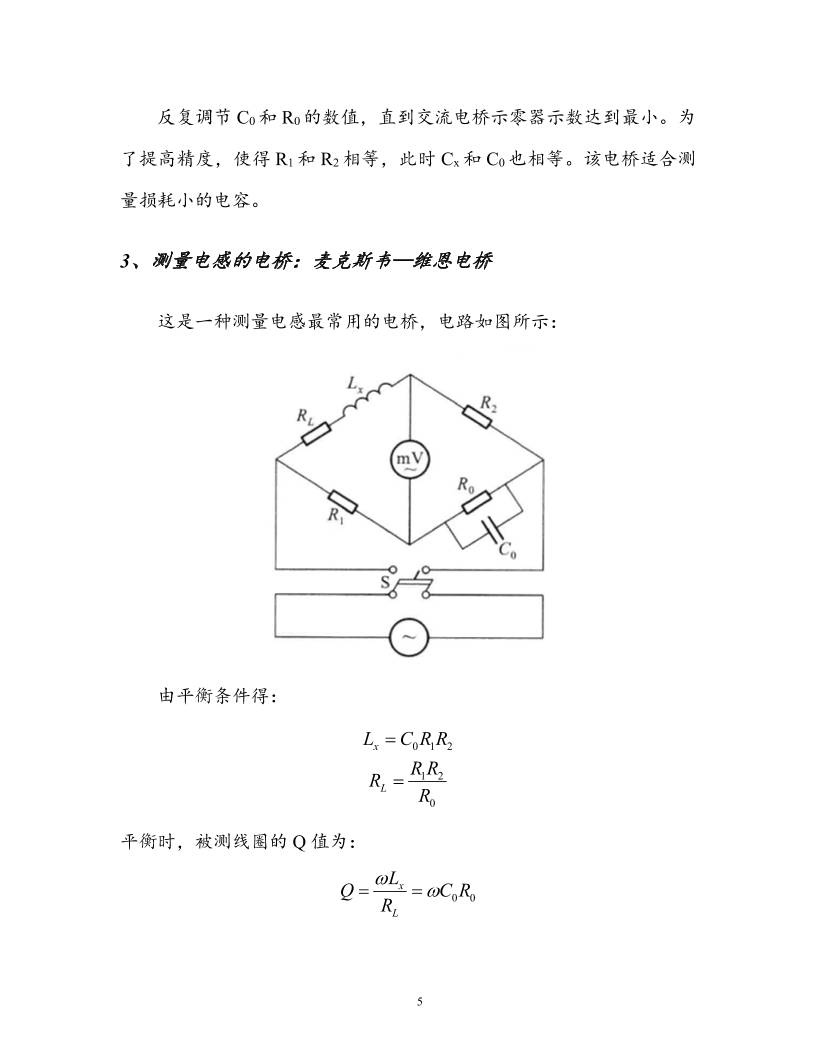
1
〖实验二十七〗
交 流 电 桥
实验时间 2015年 4月 14日
报告时间 2015年 4月 15日
祁周 1300011454
周二下午第 2组 3号
〖目的要求〗
1、学会使用交流电桥测量电容和电感及其损耗；
2、了解交流桥路的特点和调节平衡的方法。
〖仪器用具〗
函数信号发生器，ZX96型电阻箱 3个，RX7-0A型十进式电容箱，
Gx3/2型十进式电感箱，待测电容，待测电感，数字多用电表，开关，
导线若干。
ZX96型直流电阻箱参数
档位 ×10kΩ ×1kΩ ×100Ω ×10Ω ×1Ω ×0.1Ω
精度 ±0.1% ±0.1% ±0.1% ±0.1% ±0.5% ±2%
2
Gx3/2型电感箱参数
精度：2%
自感/mH 1 2 3 4 5 6 7 8 9 10
直流电阻/Ω 0.82 1.69 2.46 2.85 3.75 4.49 4.83 5.26 6.13 6.86
RX7-0A型电容箱参数
工作电压：250VAC，零容量：C12+C20=72pF
档位 ×0.1μF ×0.01μF ×0.001μF ×0.0001μF
精度 ±0.5% ±0.65% ±2% ±5%
〖实验原理〗
1、交流电桥及其平衡条件
3
交流电桥的原理电路如图所示，Z1、Z2、Z3、Z4、分别为 4个桥臂
的复阻抗。调节各臂阻抗，使电桥达到平衡，即 A和 B两点间的电位
差为零，此时有：
31
2 4
ZZ
Z Z


 
这就是交流电桥的平衡条件。将它用复指数形式表示，可化为：
31
2 4
1 2 3 4
ZZ
Z Z
   

  
由此可见，交流电桥平衡时，除了阻抗大小满足比例关系式外，阻抗的
相角还要满足一定关系，这是它和直流电桥的主要差别。
为了配置简单，很多交流电桥常用纯电阻作为其中的两个臂。由相
位关系，如果纯电阻作为相邻的两个臂，则其他两个臂必须都是电感性
的或都是电容性的阻抗。如果相对两个臂是纯电阻，则其他两个臂必须
一个是电感性的，另一个是电容性的阻抗。
2、测量实际电容的电桥
实际电容的介质不是理想的介质，在电路中要损耗一部分能量，故
其等效电路可看做是一个纯电容 Cx和损耗电阻 RC的串联或并联。实验
中是看成二者串联。
由于有损耗存在，所以正弦交流电通过它时，电容两端的电压与通
过的电流之间的相位差φ不是 90 而是 90   。φ是电容器端电压与
4
电流之间的相位差，δ称为电容器的损耗角，它随损耗电阻 RC的增加而
变大，是衡量电容质量优劣的参数。为了方便，用损耗角正切来表示，
称为损耗，
tan CR C  
测量电路如图，C为标准电容，它的损耗电阻在低频时实际近于零；
为了与 RC相平衡，又串联了电阻 R0。根据平衡条件：
1 0 2
0
1 1
C
x
R R j R R j
C C 
   
     
   
令其两端实部虚部分别相等：
2 1
0 0
1 2
0 0
,
tan
x C
C x
R RC C R R
R R
R C R C  
 
 
5
反复调节 C0和 R0的数值，直到交流电桥示零器示数达到最小。为
了提高精度，使得 R1和 R2相等，此时 Cx和 C0也相等。该电桥适合测
量损耗小的电容。
3、测量电感的电桥：麦克斯韦—维恩电桥
这是一种测量电感最常用的电桥，电路如图所示：
由平衡条件得：
0 1 2
1 2
0
x
L
L C R R
R RR
R


平衡时，被测线圈的 Q值为：
0 0
x
L
LQ C R
R
  
6
式中：C0和 R0为独立变量，反复调节可以使电桥很快达到平衡。此电
桥只适合测量低 Q值的线圈。
4、交流电桥的收敛性
要使交流电桥达到平衡，至少需要选择两个调节参量，经反复调节，
使电桥逐步趋于平衡。但是，不是任选两个参量调节都能使电桥达到平
衡；而选择的调节参量不同，使电桥趋于平衡的快慢也不一样。用电桥
收敛性来表示能否通过调节使电桥逐步达到平衡，而收敛性的好坏则反
映电桥达到平衡的快慢。
对测量电感 L的麦克斯韦桥，如上图，由平衡条件可得：
 0
1
0
2
1
0
2
x
L L
RL L
R
RR R R
R

 
7
这里可调参量较多，有 R1、R2、C0、L0和 R0，选择哪两个作为可
调参量，电桥的收敛性较好呢？将交流毫伏表的内阻近似为正无穷，可
得：
  
2 3 1 4
1 2 3 4
AB
Z Z Z Zu u
Z Z Z Z


 
当电桥接近平衡时，表达式的分子接近于 0，分母却比较大；此时
若微调各参量，分母的相对改变量很小，几乎不变，uAB的大小几乎正
比于表达式的分子的大小。如果在复数平面上以横坐标轴代表 Z的实部
Re Z，纵轴代表 Z的虚部 Im Z，令：
 
 0
2 3 2
1 4 1 0 0
L x
L
A Z Z R R j L
B Z Z R R R j L
N A B


  
   
 


 
在复数平面上作 A和 B，当所选的调节参量使 A和 B两个矢量之差 N
为零时，零示器指零，电桥达到平衡。
下面分析调节各个参量 A或 B矢端变化的轨迹，参见下图：
8
(1)调节 R1：调 R1使矢量 B的斜率不变，只是长度改变，B的矢端
轨迹为 Oa线[见图 a]；
(2)调节 R2：调 R2使矢量 A的斜率不变，只是长度改变，A的矢端
轨迹为 Ob线[见图 a]；
(3)调节 L0：调 L0使 B的实数部分不改变，只是虚数部分改变，B
的矢端轨迹为 cd线[见图 a]；
(4)调节 R0：调 R0使 B的虚数部分不变，只是实数部分改变，B的
矢端轨迹为 ef线[见图 a]。
由图 b可见，如果选择 L0和 R0为调节参量，只需调节 R0使 B到
g1点，再调节 L0，B与 A重合，电桥达到平衡。或先调节 L0到 g2点，
再调 R0，同样只经过两次调节，电桥就达到平衡。
在实验中，R0用六钮电阻箱，可认为数值是连续变化的，而 L0用
一钮十进式电感箱，不是连续可调，所以测电感时只能将 L0放在与 Lx
接近的数值后，调节 R0使 B沿 eb线移至"1"[见图 c]，再选择调 R2使 A
沿 Ob线移至"2"，每调节一次只能使 N在该情况下达到最小，如此反复
调节 R0和 R2，最后便 A和 B的矢端均达到 b点，此时 N=0，电桥调节
达到平衡。从平衡条件式中也能看出，两个平衡条件中都含有 R2，因此
R2的每一次改变对两个平衡条件都有影响，互相牵制，必须反复调节。
因此，在实际工作中很少选择 R2这样的参量来调节电桥平衡。而在上
9
文中所介绍的前两种电桥，由于两个互相独立的变量 C0和 R0均可视为
连续变化的，故收敛性均较好，是比较实用的电桥。
〖实验内容〗
用函数信号发生器提供频率约为 1kHz、电压为 4V的正弦交变电压。
用数字多用电表的交流毫伏挡作零示器。
1、测电容
测量一个纸质电容器及一个电解电容器的电容及损耗电阻，并计算
它的损耗，电路图实验原理中对应的图，其中 R1、R2、R0均用电阻箱，
R1和 R2选用几百欧姆为宜。标准电容 C0用十进式电容箱，它的损耗电
阻在低频时很小。
2、测电感
用麦克斯韦桥和麦克斯韦—维恩电桥分别测量同一无铁芯电感器
的电感 Lx和损耗电阻 RL并计算电感线圈的Q值，并比较两桥的收敛性。
〖数据记录〗
使用⑨号盒子中的元件进行测量。
10
1、纸质电容
R1=R2=500Ω；
C0=0.2353μF，R0=2.8Ω；
Umin=0.16mV，f=0.9991kHz。
2、电解电容
R1=1kΩ，R2=10kΩ；
C0=0.6576μF，R0=44.8Ω；
Umin=0.00mV，f=998.13Hz。
3、麦克斯韦—维恩桥测电感
取 R1=R2=150Ω，f=997.88Hz；先取 R0=2250Ω
i R0/Ω C0/μF Uab/mV
1 225 0.435 272
2 215.8 0.435 1.07
3 215.8 0.4363 0.00
4、麦克斯韦桥测电感
取 R1=2kΩ，首先调节 L0到 10mH，其直流电阻为 6.86Ω；先取
R0=100Ω。
11
i R0/Ω R2/Ω Uab/mV
1 100 2045.0 4.20
2 99.4 2045.0 2.25
3 99.4 2041.2 1.67
4 99.3 2041.2 1.45
5 99.3 2038.9 1.31
6 99.2 2038.9 1.01
7 99.2 2037.8 0.95
8 99.1 2037.8 0.76
9 99.1 2036.4 0.60
10 99.0 2035.2 0.23
11 99.0(98+0.1*10) 2034.9 0.22
12 99.0(98+0.1*10) 2034.8 0.18
〖数据处理及结果〗
（使用⑨号盒子中的元件）
1、纸质电容
   
   
1 2
0 0
500.0 0.6 , 500.0 0.6 ;
0.235 0.003 , 2.80 0.04 .
R R
C F R
     
    
12
 
 
01 2
01 2
2
0
1
22 2
1 2 0
1
0
2
22 2
1 2 0
0 0
0.235
1.483%
0.003
0.235 0.003
2.80
1.453%
0.04
2.80 0.04
tan 4.1
x
C
C
x
C CR R
x
C
x
C
R RR R
C
R
C
RC C F
R
C R R C
F
C F
RR R
R
R R R R
R
R C

  
 

  

 
 
    
       
     
 
  
  
    
       
     
  
   
 
 
0 0
3
2 2 2
tan
0 0
3
tan
3
306 10
2.06%
tan
0.085 10
tan 4.13 0.08 10
R C f
R C f


  







     
        
    
  
   
2、电解电容
   
   
 
1 2
0 0
1.000 0.006 , 10.000 0.006 ;
0.658 0.003 , 44.8 0.1 ;
998.13 0.01 .
R k R k
C F R
f Hz

     
    
 
13
 
 
01 2
01 2
2
0
1
22 2
1 2 0
1
0
2
22 2
1 2 0
0 0
6.58
0.7835%
0.05
6.58 0.05
4.48
0.6349%
0.0284
4.48 0.03
tan 0.1
x
C
C
x
C CR R
x
C
x
C
R RR R
C
R
C
RC C F
R
C R R C
F
C F
RR R
R
R R R R
R
R C

  
 

  

 
 
    
       
     
 
  
  
    
       
     
  
   
 
0 0
2 2 2
tan
0 0
3
tan
8487
0.5860%
tan
1.08 10
tan 0.185 0.001
R C f
R C f


  




     
        
    
  
  
3、麦克斯韦—维恩桥测电感
   
   
 
1 2
0 0
150.0 0.6 , 150.0 0.6 ;
0.436 0.003 , 215.8 0.6 ;
997.88 0.01 .
R R
C F R
f Hz

     
    
 
14
 
 
01 2
01 2
0 1 2
22 2
1 2 0
1 2
0
22 2
1 2 0
9.8100
0.963%
0.094
9.81 0.09
104.263
0.630%
0.657
104.3 0.7
x
x
L
C
x
L CR R
x
L
x
L
RR R R
L
R
C
x
L
L C R R mH
L R R C
F
L mH
R RR
R
R R R R
R
LQ C
R
  
 
  

 
 
    
       
     
 
  
  
    
       
     
  
   
 
0 0
0 0
2 2 2
0 0
0.58992
0.742%
0.0044
0.590 0.004
R CQ f
Q
R
Q R C f
Q
  


     
        
    
 
  
4、麦克斯韦桥测电感
   
 
   
0
1 2
0
0
2.000 0.006 , 2.035 0.006 ;
10.0 0.1 mH,R 6.86 ;
99.0 0.1 ; 997.88 0.01 .
L
R k R k
L
R f Hz
     
   
    
15
 
 
01 2
0
0 01 2
0
1
0
2
22 2
1 2 0
1
0
2
22 2
1 2 0
9.828
1.0849%
0.106
9.8 0.1
104.0393
0.4311%
0.4485
104.
x
x
LL
L
x
L LR R
x
L
x
L L
R RR R R
L L
R
C
RL L mH
R
L R R L
F
L mH
RR R R
R
R R R R R
R
  
 
   

 
    
       
     
 
  
   
    
              
  
   
0
00 0
0
0
0
22 2
0 0
0 0.4
0.592279
1.004%
0.005949
0.592 0.006
L
x
L L
R RLQ f
L
Q
L LQ
R R R
Q L R R f
Q
 
  

 
  

    
             
 
  
〖思考与讨论〗
1、麦克斯韦—维恩桥测电感时，电桥达到平衡的过程图
对麦克斯韦—维恩图，按实验原理中图，有：
16
     
1 1 2
0
0
3 4 2
1 21 2
1 2 4
00
00
1 2 3 4
1 2 3 4
1 2 4
0
1 2 0
3
1 2 4
1, ;1
, .
1
11
1
1
1 1 1
L x
L xL x
AB
L x
Z R Z
j C
R
Z R j L Z R
R j LR j L R RR R
Z Z Z j Cj C
RRu u u
Z Z Z Z Z Z Z Z
Z Z Z
R j L j C
R R R
u
Z
Z Z Z




 
 

  
 
   
   
    
   
 
  
  
  
   
  
快达到平衡时，分子趋于零；分母变化极小，而且它的值相对于分
子比较大。因此可近似认为 uAB与分子成正比，故此时电桥平衡的过程
大致与分子趋于零的过程相当。那么可以只讨论分子部分大小随参量的
变化过程：
1 2
0
0
1
0
L xR j LA
R R
B j C
R
N A B




 
  


 
所以，通过调节 R0和 C0的值，电桥达到平衡的过程可图示为：
17
2、麦克斯韦桥测电感时，uAB无法达到很小的解释
在这个实验中，uAB所能达到的最小值是 0.18mV，即电桥没能达到
完全理想的平衡。但是，在这个位置附近微调 R0和 R2的值，uAB都会
显著地增大，故当前的参数设置已经是所能达到的最接近平衡位置的参
数值了。对于 R0，我将 99.0Ω的阻值调为(98+0.1*10)Ω时，毫伏表的示
数仍有较大变化。这说明，电阻箱在 R0这个值附近可能存在着阻值制
作的不精确，以至于微小的调节会导致较大的阻值变化，因此电桥不能
够很好地达到平衡。
18
3、如何提高测量精度
使用电容箱、电感箱、电阻箱调节时应注意：所得元件数值的极限
误差应该用档位最高示值（10×）乘准确度等级。因此，如果使用了该
档位的小示数，即 1×或 2×，那么此时的相对不确定度就比较大，这也
会影响到间接测量量的的精度。
另外，应该利用不太准确的标称值，将所用到的桥臂电阻调为近似
相等。这是因为电阻箱的低档位精度较差，高档位精度较高，所以两个
电阻在相差较大时，其中阻值较小桥臂电阻的相对不确定度会比较大，
影响间接测量量的精度。
4、如何尽快达到电桥平衡
应该先根据不太精确的标称值将所用元件调至大致平衡。这样，在
uAB的表达式中，分子会很小，而每个元件的参数变化较小，因此，uAB
近似和分子成正比，可以利用过程图中所示路径很快调平。否则，在偏
离平衡较远的位置，元件参数需要变化很大，uAB不与分子近似成正比，
毫伏表的示数不能够很好地表示电桥平衡达到的程度，所以电桥平衡调
节较为缓慢。