概要信息：

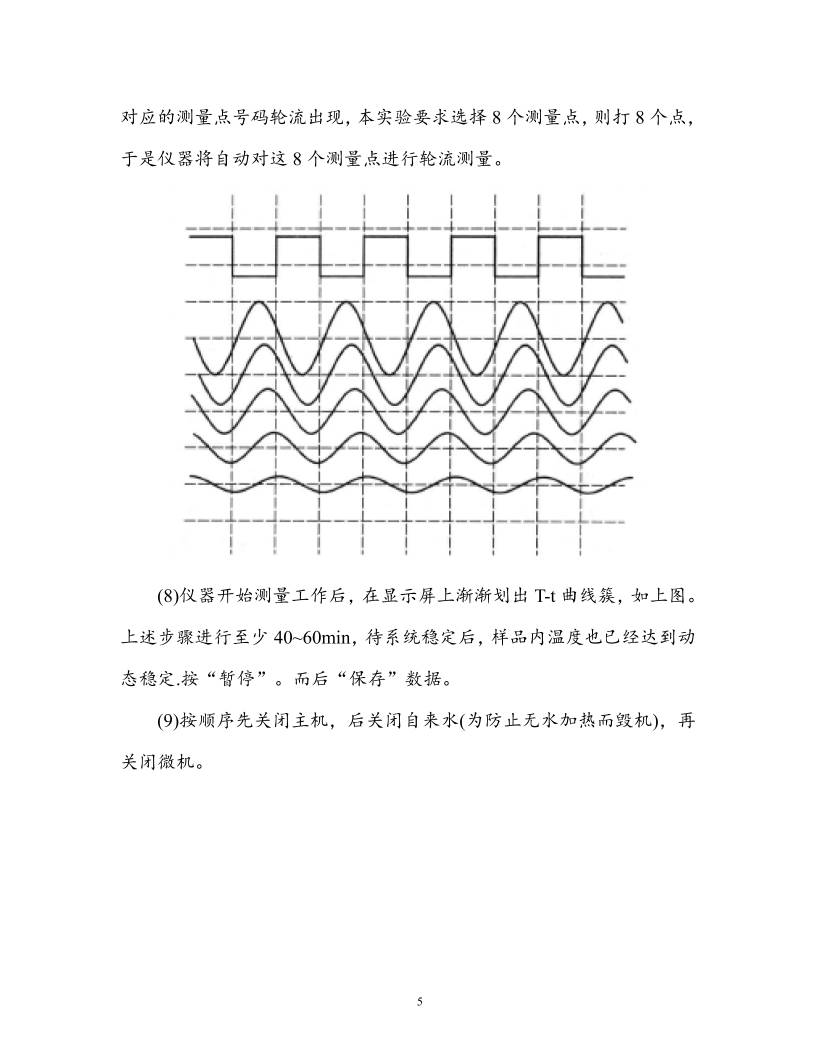
1
〖实验二十五〗
动态法测定良导体的热导率
实验时间 2015年 4月 28日
报告时间 2015年 4月 29日
祁周 1300011454
周二下午第 2组 3号
〖目的要求〗
1、测定良导体的热导率；
2、学习一种测定材料热导率的方法；
3、了解动态法测定良导体的特点和优越性；
4、认识热波，加强对波动理论的理解。
〖仪器用具〗
热导率动态测量仪，微机。
2
〖实验原理〗
1、热流方程
本实验采用非稳态法测定良导体的热导率。取棒状样品，假定热量
仅沿一维传播。取一小段棒元，根据傅里叶导热定律，单位时间内在单
位等温面上沿温度降低方向流过某垂直于传播方向的热流密度为：
q T
t t
 
 
 
式中：κ为待测材料的热导率。由导热定律可推得热流方程：
2
2 ,T T
t x c
 

 
 
 
式中：α称为热扩散率。
2、热波方程
热流方程的解将各点的温度随时间的变化表示出来，具体形式取决
于边界条件，若令热端的温度围绕 T0按简谐规律变化，即：
0 sinmT T T t 
式中：Tm为热端的最高温度；ω为热端温度变化的角频率。
假设另一端无反射并保持恒定温度为 T0，则式热流方程的解也就是
棒中各点的温度，即：
0 exp sin
2 2mT T kx T x t x 
 
   
          
   
3
式中的 T0是直流成分；k是线性成分的斜率。
从上式中可以看出：
(1)当热端（x=0）温度按简谐方式变化时，这种变化将以衰减波的
形式在棒内向冷端传播，称为热波，也就是温度波。
(2)热波波速
2v 
(3)热波波长
22  


因此在角频率。已知的情况下，只要测出波速或波长就可以计算出
α然后再由 c



计算出材料的热导率κ。由热波波速公式，可得：
2 2
2
4
2
4 period
cv v c T
c f
v   
  
   
式中：f，Tperiod分别为热端温度按简谐变化的频率和周期。
从上述原理可知实现热导率测量的关键是:
①实现热量的一维传播；
②实现热端温度随时间按简谐形式变化的边界条件。
本实验采取的热波法，特点是当热量在样品中传播时，样品中各点
的温度不像稳态法那样必须保持恒定，只要给定适当边界条件，可以做
到样品上各点的温度均可随时间进行简谐变化，利用这种变化可以很容
易测出热波波速，进而可计算出样品材料的热导率。
4
〖实验内容〗
1、认识和调节实验装置
(1)观察仪器面板，了解仪器的功能；
(2)观察并了解几个水龙头及进、出水管的功能；
(3)调节样品冷端的冷却水流量至 300mL/min，在开启微机后再调节
样品热端冷却水的流量小于 700mL/min(具体根据微机屏幕上显示的棒
上各点温度变化曲线来判断和调节)。
2、了解数据采集过程并测样品各点温度随时间的变化曲线
(1)按下“工作方式”开关，选择“程控”工作方式。
(2)打开微机，启动“热导率动态测量”程序。
(3)设置脉动热源周期为 180s。
(4)选择铜样品进行测量。
(5)设置 x，y轴的单位坐标，x方向为时间，单位为 s，y方向代表
信号强度，单位为 mV（每 mV约为 0.1℃）。
(6)在“测量状态显示”栏中，会自动显示测量位置、运行时间及信
号幅度。
(7)在“选择测量点”栏中选择几个测量点，单击鼠标，在“操作”
栏按“测量”。开始测量后，程序操作界面的“测量位置”所选的几个
5
对应的测量点号码轮流出现，本实验要求选择 8个测量点，则打 8个点，
于是仪器将自动对这 8个测量点进行轮流测量。
(8)仪器开始测量工作后，在显示屏上渐渐划出 T-t曲线簇，如上图。
上述步骤进行至少 40~60min，待系统稳定后，样品内温度也已经达到动
态稳定.按“暂停”。而后“保存”数据。
(9)按顺序先关闭主机，后关闭自来水(为防止无水加热而毁机)，再
关闭微机。
6
〖数据记录与处理〗
1、使用软件自动拟合正弦曲线处理
使用样品 铜
比热 c 385J/kg/K
密度ρ 8920kg/m3
相邻热电偶间距 L 2cm
起始时间/s 2100 终止时间/s 2800
输入波形序号 1 输出波形序号 2
平均峰-峰延迟时间/s 6.96
周期 T/s 174.4262
最终结果 热导率κ 393.6126 J/K/m/s
起始时间/s 2100 终止时间/s 2800
输入波形序号 4 输出波形序号 5
平均峰-峰延迟时间/s 6.96
周期 T/s 174.4262
最终结果 热导率κ 393.6126 J/K/m/s
起始时间/s 2100 终止时间/s 2800
输入波形序号 6 输出波形序号 7
7
平均峰-峰延迟时间/s 6.96
周期 T/s 174.4262
最终结果 热导率κ 393.6126 J/K/m/s
起始时间/s 3800 终止时间/s 5000
输入波形序号 4 输出波形序号 5
平均峰-峰延迟时间/s 6.555
周期 T/s 182.057
最终结果 热导率κ 463.1671 J/K/m/s
起始时间/s 3800 终止时间/s 5000
输入波形序号 6 输出波形序号 7
平均峰-峰延迟时间/s 6.555
周期 T/s 182.057
最终结果 热导率κ 463.1671 J/K/m/s
起始时间/s 3950 终止时间/s 5000
输入波形序号 2 输出波形序号 6
平均峰-峰延迟时间/s 6.96
周期 T/s 190.0725
最终结果 热导率κ 438.7936 J/K/m/s
将所得的六个测量值取算术平均得：κ=424.3276J/(K·m·s)
8
2、取一组数据拟合延迟时间
(1)取一组峰序列，记录峰对应的时间（单位：秒）
2636.18 2643.56 2650.55 2657.74
2665.12 2671.5 2678.49 2686.07
做线性拟合：
斜率
值 7.07274
标准差 0.0432
数据 线性回归系数 0.99987
 
 
2
393.34
4 period
l
t c
JT K m s



    
(2)取一组谷序列，记录谷对应的时间（单位：秒）
9
2553.55 2559.53 2566.72 2573.90
2579.89 2588.28 2594.29 2601.45
做线性拟合：
斜率
值 6.90202
标准差 0.07997
数据 线性回归系数 0.99953
 
 
2
413.04
4 period
l
t c
JT K m s



    
(3)再取一组谷序列，记录谷对应的时间（单位：秒）
4525.68 4532.86 4539.65 4546.64
10
4553.42 4561.02 4568.09 4575.08
做线性拟合：
斜率
值 7.05762
标准差 0.03344
数据 线性回归系数 0.99992
 
 
2
395.03
4 period
l
t c
JT K m s



    
取算数平均值，得：κ=400.47J/(K·m·s)