概要信息：

¢›˜ *	1 y–
Xhè 1300011329
±e5|11Ò
¢žm2014c1125F
wžm2014c1128F
1 8‡¦
(1) yÙVdA½Æ
(2) *	Vòy–
(3) )Ú*	1 
(4) 
))Úu 1‡Ú¤ì
(5) ݺ)Úu 1^‡Ú{
2 ¤ì^ä
 1º,  ¡, )œ¬, 1/2Å¡, 1/4Å¡, He-Ne -1ì, ?1, À¡æ, 1äŒ, 1
>+, 1>6w«ì
3 ¢n
3.1 ÙVdA
1lòǏn10Ÿ£~X˜í¤\òǏn20Ÿ£~XÀæ¤.¡, 
\q÷v
θB = arctan
n2
n1
ž, ‡1=¤ 1, ÙÄ¡R†u\¡. θB¡ÙVdA, þª=ÙVdA½Æ. Ø
J, en1L«´˜íòÇ, þªŒ¤
θB = arctann2
,	, XJg,1±ÙVdA\Àæ¡æþ, ²Lõg‡ßÑ51˜„´Ü
© 1. XJÀæ¡ê8éŒ, KÑ1Cq‚ 1.
1
3.2  ¡
g,1²L ¡¬C‚ 1.  ¡QŒ±Šå ì¦^, Œ±Šu ì¦
^.
3.3 Ŭ¡
e¦‚ 1R†\˜ß1¡²1u1¶, þݏd¬¡, K1¬©¤Ï~1Ú
š~1. \1̏A§Е†1¶Yθ,\¬¡o1Úe1Ì©OA sin θ
ÚA cos θ,у 
ϕ =
2π
λ0
(no − ne)d
ª¥λ0´13ý˜¥Å, noÚne©O´o1Úe1òÇ.
ù«U¦ƒpR†Ä²¡ 1)˜½ƒ ¬¡Ò‰Å¡.
XJ±²1uÅ¡1¶•x‹I, R†u1¶•y‹IÑo1Úe1Œ^ü‡{
ЧªL«:
x = Ae sinωt
y = Ao sin(ωt+ ϕ)
˜„`5, ù´˜‡ý 1. ´
ϕ = 2kπ
½
ϕ = (2k + 1)π
ž, ÜÄC¤ЕØÓ‚ 1.˜«œ¹§¬¡þÝ
d =
(2k + 1)
no − ne
λ
2
Œ¦o1Úe1) (2k+1)λ
2 1§, ù¬¡¡‰ŒÅ¡.

ϕ = (2k + 1)π2 (k = 1, 2, 3..)ž, ÜЧzý§ x2
A2
e
+ y2
A2
o
= 1 ùž¬¡þ
Ýd = (2k+1)
no−ne
λ
4 , ¡‰
1
4Å¡. §U¦‚ 1UC , C¤ý 1.
AO´\1Ä¡†Å¡1¶Yθ = 45◦ž, Ae = Ao, =¼ 1.
3.4  1¼

ý 1, ¦g,1ÏL˜‡å ìژ‡Å¡=Œ. då ìÑ 1\
Å¡¥ž, ‡ÙĐ•Ø†Å¡1¶²1½R†, Ò¬©)¤o1Úe1, BLÅ¡
ž3§‚ƒmÒk˜½N\ƒ δ. ÑÅ¡ƒ, §‚3˜å˜„´Ü¤ý 1.k
ùü¡å1ƒmƒ u±π/2…̃Ӟ, âkŒU 1.
2
4 ¢SN
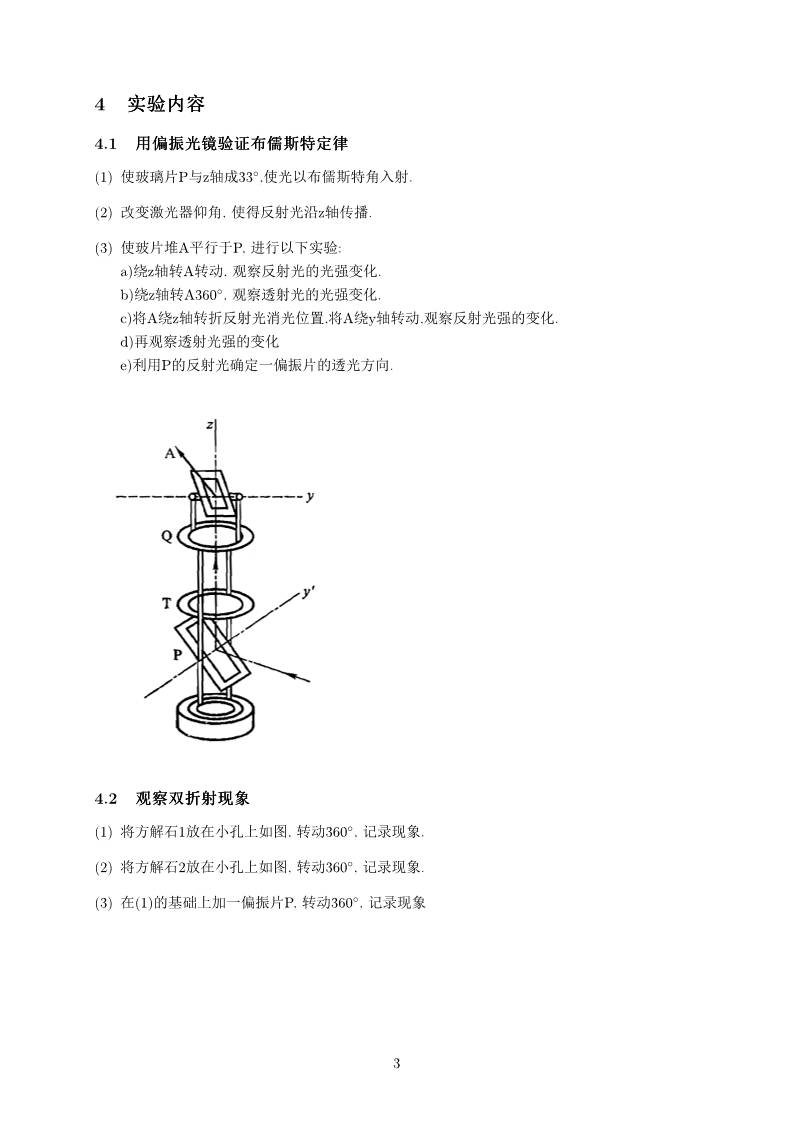
4.1 ^ 1ºyÙVdA½Æ
(1) ¦Àæ¡P†z¶¤33◦,¦1±ÙVdA\.
(2) UC-1ì, ¦‡1÷z¶DÂ.
(3) ¦À¡æA²1uP, ?1±e¢:
a)7z¶=A=Ä, *	‡11rCz.
b)7z¶=A360◦, *	ß11rCz.
c)òA7z¶=ò‡1ž1 ˜,òA7y¶=Ä,*	‡1rCz.
d)2*	ß1rCz
e)|^P‡1(½˜ ¡ß1•.
4.2 *	Vòy–
(1) ò)œ1˜3šþXã, =Ä360◦, P¹y–.
(2) ò)œ2˜3šþXã, =Ä360◦, P¹y–.
(3) 3(1)Ä:þ\˜ ¡P, =Ä360◦, P¹y–
3
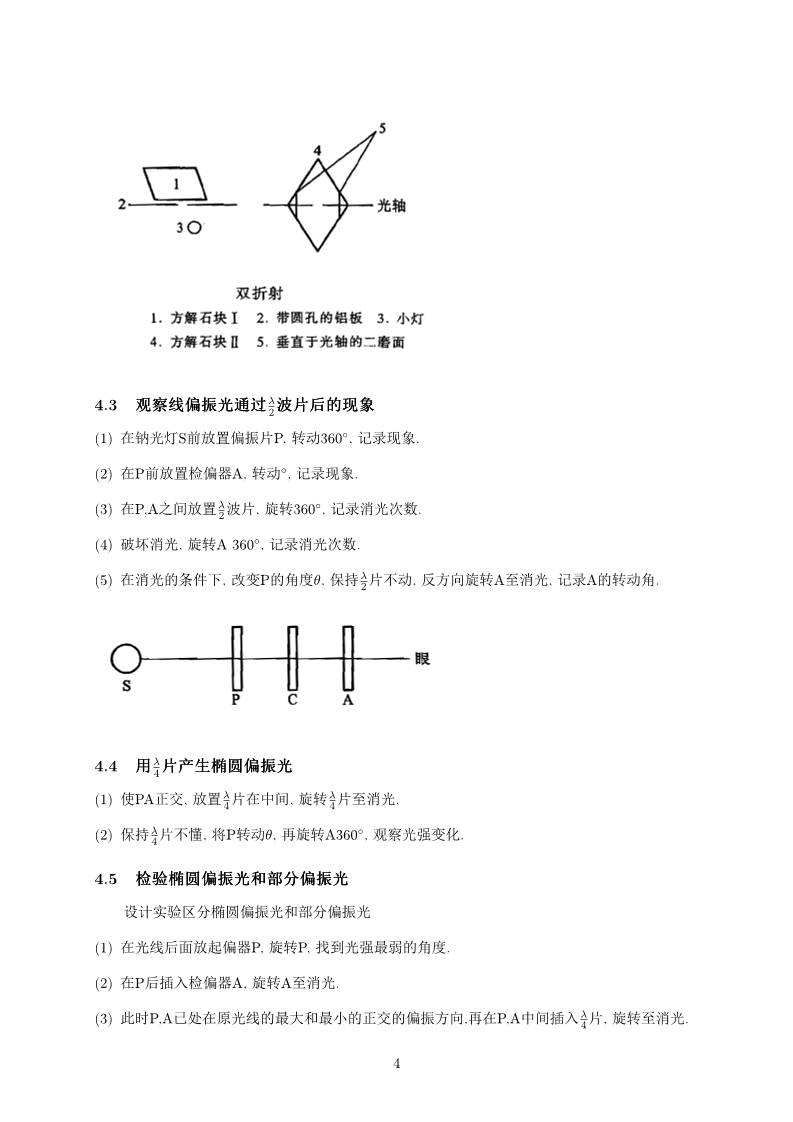
4.3 *	‚ 1ÏL λ
2
Å¡y–
(1) 3?1Sc˜˜ ¡P, =Ä360◦, P¹y–.
(2) 3Pc˜˜u ìA, =Ä◦, P¹y–.
(3) 3P,Aƒm˜˜λ
2Å¡, ^=360◦, P¹ž1gê.
(4) »€ž1, ^=A 360◦, P¹ž1gê.
(5) 3ž1^‡e, UCPÝθ, ±λ
2¡ØÄ, ‡•^=A–ž1, P¹A=Ä.
4.4 ^ λ
4
¡)ý 1
(1) ¦PA, ˜˜λ
4¡3¥m, ^=λ
4¡–ž1.
(2) ±λ
4¡ØÃ, òP=Äθ, 2^=A360◦, *	1rCz.
4.5 uý 1ÚÜ© 1
O¢«©ý 1ÚÜ© 1
(1) 31‚¡˜å ìP, ^=P, é1rfÝ.
(2) 3P\u ìA, ^=A–ž1.
(3) džP,A®?31‚ŒÚ •,23P,A¥m\λ
4¡, ^=–ž1.
4
(4) 3P,A¥m\λ
4¡, ^=–ž1.
(5) ’P, Nu ìA. XJŒ±ž1, Ò´ý 1. XJØUž1, Ò´Ü© 1.
5 y–£ã9êâL‚
5.1 ^ 1ºyÙVdA½Æ
a) ÄkN
A†P²1, òA7z¶^=L§¥,uy‡11r§ëY±Ï5Cz,A
O´3=L90◦ž‡1Cuž1(*	
˜ý, ˜ýduvkɶu´˜ï
),ù´
dul-1ìuÑ1±ÙVdA²LP‡,®²Cqs•‚ 1,ùžÓ±
ÙVdA\AžTЏp•,Ïdه11rA".í{1rßÿ´duÃ
{î‚N\ÙVdA¤—.
b) *	ß1uy3±Ï5Cz,´ÙCzéØ´	ú,
…Cz†‡1Ѓ‡,l
1ÏþÅðéN´n).
c) NA=þã‡1Až1 ˜,2¦Ù7y¶^=,uyT?‡1r4Š.
d) ӞT ˜´ß1r4ŒŠ,´3^=L§¥Czزw.
e) ò˜ ¡˜uQ?^=,uy¬k±Ï5ž1y–,l
y¢
T1‚kРÝ,
Až1••= ¡ •
5.2 *	Vòy–
(1) *	)œ˜,Œ±wü‡ß”,3^=L§¥,k˜‡”AØÄ, ˜‡¬‹X^=,Œ
±íÿcö´o1,öe1;AO/,k˜¬)œ„¬kÚÑy–,…ØØ´o1„´e1,ß
1ôÚѬ‘X^=
Cz;ßL ¡*	ž,¬uy‘X ¡^=,ü‡”:¬
OÑyž1,ƒ…Œ90◦.
(2) *	)œ,vU¤õ/Xýτé1¶,ÏdEU*	ü‡”:;uyßL ¡
*	ž,lØÓý¡ÝÑ1¿Ø¬Óžž1()o1Úe1),
´U옽^S,ùŒ±
)º3¬N¥÷ØӐ•DÂ, •ƒA¬ØÓ.
(3) ßL ¡*	ÃŶ4¬uy1rÚôÚ¬‘X^=ÝØÓ
Cz.
5.3 *	‚ 1ÏL λ
2
Å¡y–
(1) ^=P˜±1rvkCz,Œ1
Cqg,1.
(2) ^=A˜±¬kügž1,üg1r4Œy–.d‚ 15ŸéN´n).
(3) 3P,Aƒm\λ
2¡¿^=˜±,¬k4gž1y–.
(4) =Äλ
2¡»€ž1,2=ÄA˜±Ø¬Ñyž1y–,¬küg1r4ŒÚüg1r
4,dž²Lλ
2¡1®Ø´‚ 1,ÏÿؘÙ.
5
(5) êâL‚Xe.Ù¥Ø
0◦,75◦Ú90◦	þÃ{ž1
θ θ
′
k 1²Lλ
2Å¡Ä=LÝ
0.0◦ 0.0◦ 0.0◦
15.0◦ 16.8◦ 31.8◦
30.0◦ 29.8◦ 59.8◦
45.0◦ 45.8◦ 90.8◦
60.0◦ 60.0◦ 120.0◦
75.0◦ 74.8◦ 149.8◦
90.0◦ 89.8◦ 189.8◦
5.4 ^ λ
4
¡)ý 1
y–P¹Xe:
å ì=ÄÝ A=360◦*	y– 1ÏLÅ¡ 
0◦ ž1, lVV2 ‚ 
15◦  ÝC, lVV2 ý 
30◦  ݍ§lVV2 ý 
45◦  ÝC0§ÄÃCz  
60◦  ÝCŒ§lVV2 ý 
75◦  ݍŒ§lVV2 ý 
90◦ ž1§lVV2 ‚ 
5.5 uý 1ÚÜ© 1
(1) 31‚¡˜å ìP, ^=P, é1rfÝ.
(2) 3P\u ìA, ^=A–ž1.
(3) džP,A®?31‚ŒÚ •,23P,A¥m\λ
4¡, ^=–ž1.
(4) 3P,A¥m\λ
4¡, ^=–ž1.
(5) ’P, Nu ìA. XJŒ±ž1, Ò´ý 1. XJØUž1, Ò´Ü© 1.
6 g9a×
(1) 31˜‡¢N1²LP‡÷ꊐ•DÂk˜½(J,Œ±|^Q‡1´‡
1:Ú\1:­Ü5ˆJ.
(2) 'uVò¢¥Ÿo)œ˜¥k˜¬¬ÑyÚÑy–±9Û)œÃ{é
1¶–8™U)û,F"P“:.
6
(3) λ
2Å¡¢(4)(5)¥,¬ÑyÃ{ž1y–,Ïÿز,ßÿ´º¡g¯K,Ó
F"P“:.
(4) ¢Ož,˜m©ÒŽÐ
On,vkU
äNŽÑŒ1öŠÚ½('
XÄLӞ=Äλ
4¡ÚA,5éž1y–),l¥N¬
ÏL¢öŠ)û¯KÚnØ
ÆSO,38ÆS¥¬õ3¿Úg.
7