概要信息：

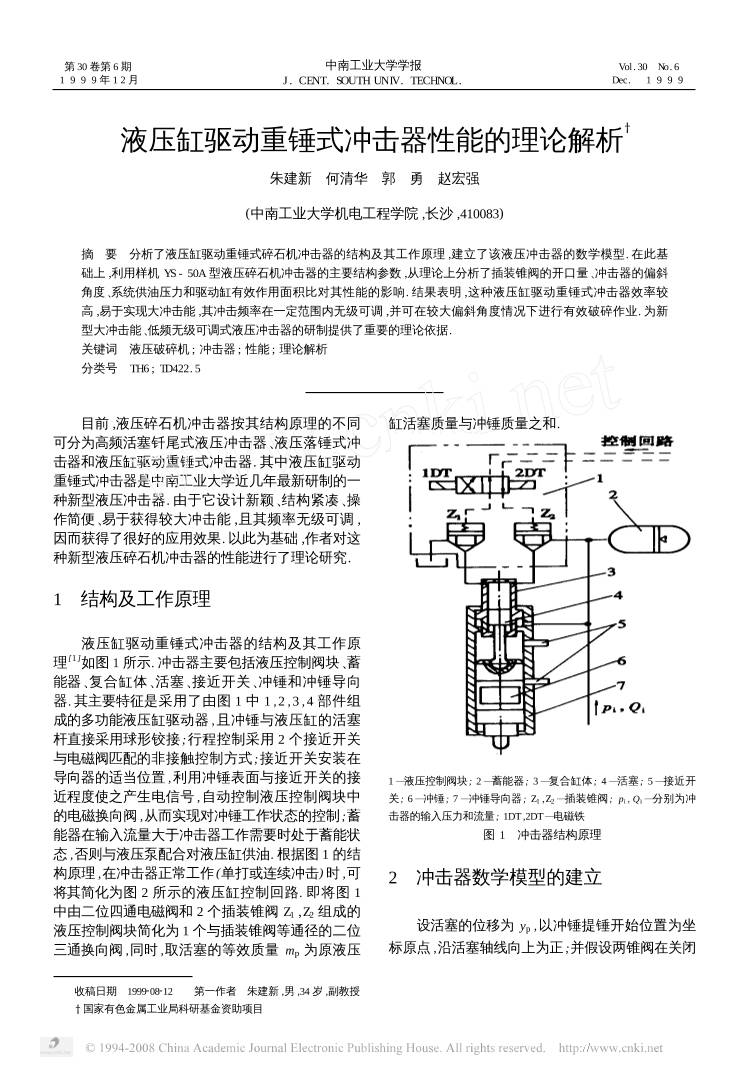
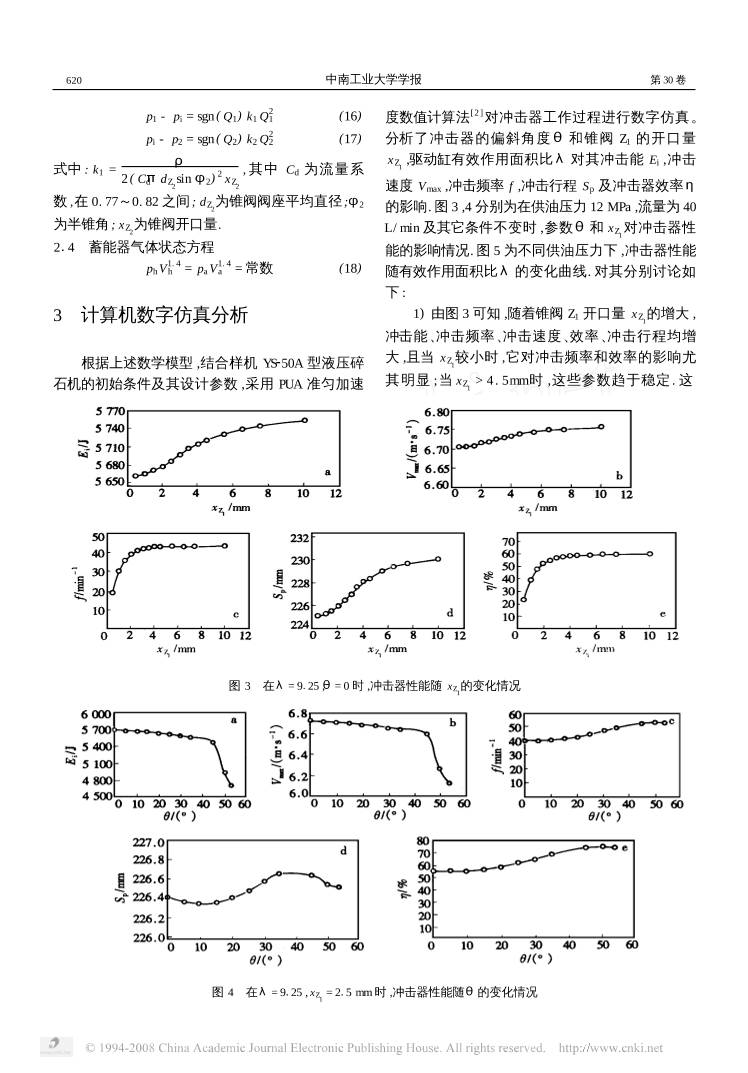
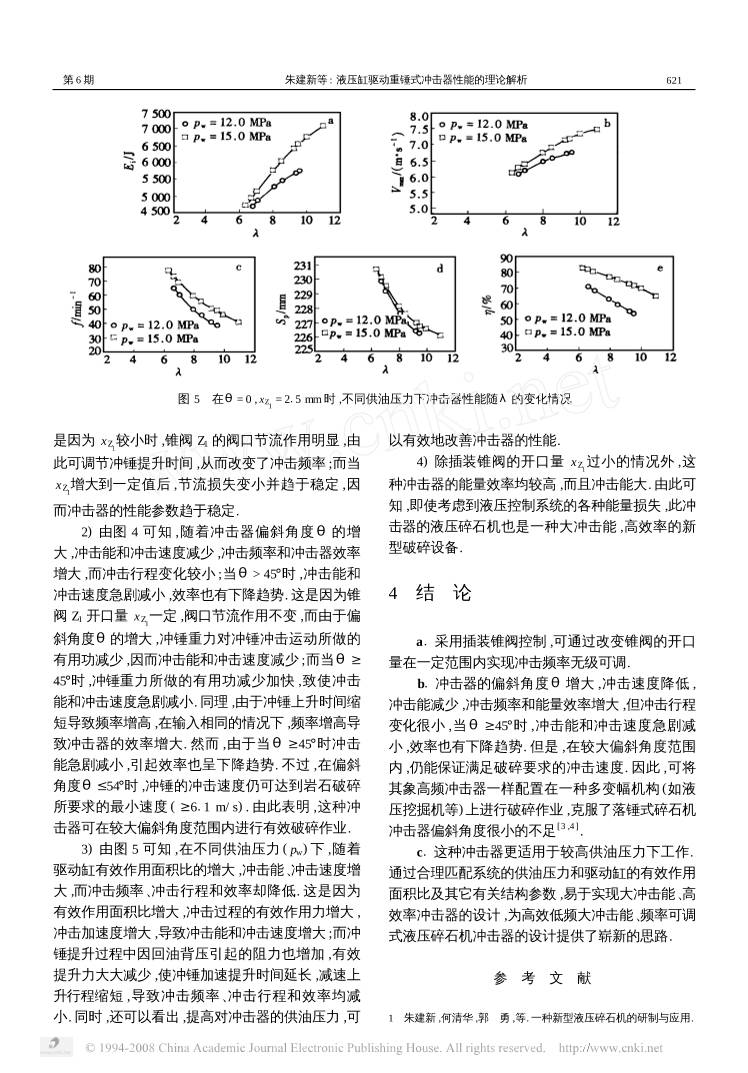
液压缸驱动重锤式冲击器性能的理论解析
­
朱建新 　何清华 　郭 　勇 　赵宏强
(中南工业大学机电工程学院 ,长沙 ,410083)
摘　要 　分析了液压缸驱动重锤式碎石机冲击器的结构及其工作原理 ,建立了该液压冲击器的数学模型. 在此基
础上 ,利用样机 YS - 50A 型液压碎石机冲击器的主要结构参数 ,从理论上分析了插装锥阀的开口量、冲击器的偏斜
角度、系统供油压力和驱动缸有效作用面积比对其性能的影响. 结果表明 ,这种液压缸驱动重锤式冲击器效率较
高 ,易于实现大冲击能 ,其冲击频率在一定范围内无级可调 ,并可在较大偏斜角度情况下进行有效破碎作业. 为新
型大冲击能、低频无级可调式液压冲击器的研制提供了重要的理论依据.
关键词 　液压破碎机 ; 冲击器 ; 性能 ; 理论解析
分类号 　TH6 ; TD422. 5
　　目前 ,液压碎石机冲击器按其结构原理的不同
可分为高频活塞钎尾式液压冲击器、液压落锤式冲
击器和液压缸驱动重锤式冲击器. 其中液压缸驱动
重锤式冲击器是中南工业大学近几年最新研制的一
种新型液压冲击器. 由于它设计新颖、结构紧凑、操
作简便、易于获得较大冲击能 ,且其频率无级可调 ,
因而获得了很好的应用效果. 以此为基础 ,作者对这
种新型液压碎石机冲击器的性能进行了理论研究.
1 　结构及工作原理
液压缸驱动重锤式冲击器的结构及其工作原
理[1 ]如图 1 所示. 冲击器主要包括液压控制阀块、蓄
能器、复合缸体、活塞、接近开关、冲锤和冲锤导向
器. 其主要特征是采用了由图 1 中 1 , 2 , 3 , 4 部件组
成的多功能液压缸驱动器 ,且冲锤与液压缸的活塞
杆直接采用球形铰接 ;行程控制采用 2 个接近开关
与电磁阀匹配的非接触控制方式 ;接近开关安装在
导向器的适当位置 ,利用冲锤表面与接近开关的接
近程度使之产生电信号 ,自动控制液压控制阀块中
的电磁换向阀 ,从而实现对冲锤工作状态的控制 ;蓄
能器在输入流量大于冲击器工作需要时处于蓄能状
态 ,否则与液压泵配合对液压缸供油. 根据图 1 的结
构原理 ,在冲击器正常工作 (单打或连续冲击) 时 ,可
将其简化为图 2 所示的液压缸控制回路. 即将图 1
中由二位四通电磁阀和 2 个插装锥阀 Z1 ,Z2 组成的
液压控制阀块简化为 1 个与插装锥阀等通径的二位
三通换向阀 ,同时 ,取活塞的等效质量 mp 为原液压
缸活塞质量与冲锤质量之和.
1 —液压控制阀块 ; 2 —蓄能器 ; 3 —复合缸体 ; 4 —活塞 ; 5 —接近开
关 ; 6 —冲锤 ; 7 —冲锤导向器 ; Z1 ,Z2 —插装锥阀 ; pi , Qi —分别为冲
击器的输入压力和流量 ; 1DT ,2DT—电磁铁
图 1 　冲击器结构原理
2 　冲击器数学模型的建立
设活塞的位移为 yp ,以冲锤提锤开始位置为坐
标原点 ,沿活塞轴线向上为正 ;并假设两锥阀在关闭
收稿日期　1999208212 　　第一作者　朱建新 ,男 ,34 岁 ,副教授
­国家有色金属工业局科研基金资助项目
第 30 卷第 6 期
1 9 9 9 年 1 2 月
　　　　　　　　　　　　
中南工业大学学报
J . CENT. SOUTH UNIV. TECHNOL.
　　　　　　　　　　　　　　
Vol . 30 　No. 6
Dec. 　1 9 9 9
状态时泄漏量为 0. 根据图 2 所示的冲击器简化模型
及其工作原理 ,在冲击器正常工作时 ,可建立如下的
数学模型.
　　p0 , p1 , p2 —分别为冲锤上升时的回油背压以及驱动缸大腔、小腔
的压力 ; A1 , A2 —分别为驱动缸大腔、小腔的有效作用面积 ; d1 , d2 —
分别为活塞和活塞杆直径 ; pa , V a —分别为蓄能器的充气压力和容
积 ; ph , V h —分别为蓄能器的工作压力和气体体积 ; θ—冲击器中心
线与垂直方向间的夹角 ; Q1 , Q4 —分别为流经锥阀 Z2 和 Z1 的流量 ,
设从驱动缸大腔流出为正 ; Q2 , Q3 —分别为流入驱动缸小腔和蓄能
器的流量 ; mp —活塞的等效质量 ; l1 —活塞与缸体圆柱面间的重叠
长度 ; S P —活塞的冲击行程 ; k1 , k4 —锥阀 Z2 , Z1 的压力损失系数 ;
k2 , k3 —相应管道的压力损失系数
图 2 　冲击器简化模型
211 　活塞 (冲锤) 动力学方程
mp
d2 yp
d t2 + B s
d yp
d t
+ sgn (
d yp
d t
) B l| p2 - p1| +
μ0 mp gsinθ= A2 p2 - A1 p1 - mp gcosθ (1)
式中 :μ0 为冲锤与导向器间的摩擦因数 ; B s =
πμl1 d1
h1 1 - ε2
+
πμl2 d2
h2 1 - ε2
, 为计算粘性摩擦阻尼系
数 ,其中μ为液压油的动力粘度 ,ε为活塞与缸体、
活塞杆与导向套间的偏心率 (设二者偏心率相同) ,
l2 为活塞杆与导向套圆柱面间的重叠长度 , h1 , h2
分别为活塞与缸体、活塞杆与导向套间的间隙高度 ;
B l =τ( l1 d1 + l2 d2 ) ±
π
2
( l1 d1 + l2 d2 ) =τ( l1 d1 +
l2 d2) +
π
2
( l1 d1 + l2 d2) sgn[
d yp
d t
( p2 - p1) ] ,为计算液
压卡紧阻尼系数. 其中τ为阻尼系数 , 是卡紧系数
与摩擦因数的乘积 ,一般为 0. 02～0. 025[2 ] .
212 　活塞加速上升阶段的其它方程 ( A2 通高压 , A1
通回油)
2. 2. 1 　流量平衡方程
Qi - Ql = A2
d yp
d t
-
dVh
d t
(2)
Q2 = Ql + A2
d yp
d t
(3)
Q3 = -
dVh
d t
(4)
Q4 = Ql + A1
d yp
d t
= Ql +λA2
d yp
d t
(5)
式中 : Ql 为驱动缸大腔与小腔间的泄漏流量 ;λ=
A1/ A2 ,为驱动缸大腔和小腔的有效作用面积之比.
2. 2. 2 　泄漏流量方程
Ql = R1 ( p2 - p1) + R2
d yp
d t
(6)
式中 : R1 =
πd1 h3
1
12μl1
(1 + 115ε2) , R2 =
πd1 h1
2
,为计算泄
漏流量的系数.
2. 2. 3 　压力2流量方程
ph - p2 = k2 Q2
2 - k3 Q2
3 (7)
pi - p2 = k2 Q2
2 (8)
p1 = p0 = k4 Q2
4 (9)
式中 : k2 =
ξ2ρ
2A2
G
2
,其中ξ2 为其集中化了的局部阻碍
系数 ,ρ为油液的密度 , A G2
为相应胶管的通流面积 ;
k3 =
ξ3ρ
2A2
G
3
,其中ξ3 为其集中化了的局部阻碍系数 ,
A G3
为相应胶管的通流面积 ;
k4 =
ρ
2 ( CdπdZ
1
sin φ1) 2 xZ
1
. 其中 dZ1
为该锥阀座平均
直径 ,φ1 为半锥角 , xZ
1
为该锥阀开口量.
213 　活塞减速上升及冲击时的其它方程 ( A1 , A2 同
时通高压油 ,驱动缸差动连接)
2. 3. 1 　流量平衡方程
Qi = ( A2 - A1)
d yp
d t
+
dVh
d t
= (1 - λ) A2
d yp
d t
+
dVh
d t
(10)
Q1 = A1
d yp
d t
+ Ql =λA2
d yp
d t
+ Ql (11)
Q2 = Ql + A2
d yp
d t
(12)
Q3 = -
dVh
d t
(13)
2. 3. 2 　泄漏流量方程
Ql = R1 ( p2 - p1) + R2
d yp
d t
(14)
2. 3. 3 　压力2流量方程
p1 - ph = sgn ( Q3) k3 Q2
3 + sgn ( Q1) k1 Q2
1 (15)
916第 6 期　　　　　　　　　　　　　　　　　　朱建新等 : 液压缸驱动重锤式冲击器性能的理论解析
p1 - pi = sgn ( Q1) k1 Q2
1 (16)
pi - p2 = sgn ( Q2) k2 Q2
2 (17)
式中 : k1 =
ρ
2 ( CdπdZ
2
sin φ2) 2 xZ
2
, 其中 Cd 为流量系
数 ,在 0. 77～0. 82 之间 ; dZ2
为锥阀阀座平均直径 ;φ2
为半锥角 ; xZ2
为锥阀开口量.
214 　蓄能器气体状态方程
ph V1. 4
h = pa V1. 4
a = 常数 (18)
3 　计算机数字仿真分析
根据上述数学模型 ,结合样机 YS250A 型液压碎
石机的初始条件及其设计参数 ,采用 PUA 准匀加速
度数值计算法[2 ]对冲击器工作过程进行数字仿真。
分析了冲击器的偏斜角度θ和锥阀 Z1 的开口量
xZ
1
,驱动缸有效作用面积比λ对其冲击能 Ei ,冲击
速度 Vmax ,冲击频率 f ,冲击行程 Sp 及冲击器效率η
的影响. 图 3 ,4 分别为在供油压力 12 MPa ,流量为 40
L/ min 及其它条件不变时 ,参数θ和 xZ1
对冲击器性
能的影响情况. 图 5 为不同供油压力下 ,冲击器性能
随有效作用面积比λ的变化曲线. 对其分别讨论如
下 :
1) 由图 3 可知 ,随着锥阀 Z1 开口量 xZ
1
的增大 ,
冲击能、冲击频率、冲击速度、效率、冲击行程均增
大 ,且当 xZ
1
较小时 ,它对冲击频率和效率的影响尤
其明显 ;当 xZ1
> 4 . 5mm时 ,这些参数趋于稳定 . 这
图 3 　在λ= 9125 ,θ= 0 时 ,冲击器性能随 xZ
1
的变化情况
图 4 　在λ= 9125 , xZ
1
= 215 mm时 ,冲击器性能随θ的变化情况
026 中南工业大学学报 　　　　　　　　　　　　　　　　　　　第 30 卷
图 5 　在θ= 0 , xZ
1
= 215 mm时 ,不同供油压力下冲击器性能随λ的变化情况
是因为 xZ
1
较小时 ,锥阀 Z1 的阀口节流作用明显 ,由
此可调节冲锤提升时间 ,从而改变了冲击频率 ;而当
xZ
1
增大到一定值后 ,节流损失变小并趋于稳定 ,因
而冲击器的性能参数趋于稳定.
2) 由图 4 可知 ,随着冲击器偏斜角度θ的增
大 ,冲击能和冲击速度减少 ,冲击频率和冲击器效率
增大 ,而冲击行程变化较小 ;当θ> 45°时 ,冲击能和
冲击速度急剧减小 ,效率也有下降趋势. 这是因为锥
阀 Z1 开口量 xZ1
一定 ,阀口节流作用不变 ,而由于偏
斜角度θ的增大 ,冲锤重力对冲锤冲击运动所做的
有用功减少 ,因而冲击能和冲击速度减少 ;而当θ≥
45°时 ,冲锤重力所做的有用功减少加快 ,致使冲击
能和冲击速度急剧减小. 同理 ,由于冲锤上升时间缩
短导致频率增高 ,在输入相同的情况下 ,频率增高导
致冲击器的效率增大. 然而 ,由于当θ≥45°时冲击
能急剧减小 ,引起效率也呈下降趋势. 不过 ,在偏斜
角度θ≤54°时 ,冲锤的冲击速度仍可达到岩石破碎
所要求的最小速度 ( ≥611 m/ s) . 由此表明 ,这种冲
击器可在较大偏斜角度范围内进行有效破碎作业.
3) 由图 5 可知 ,在不同供油压力 ( pw) 下 ,随着
驱动缸有效作用面积比的增大 ,冲击能、冲击速度增
大 ,而冲击频率、冲击行程和效率却降低. 这是因为
有效作用面积比增大 ,冲击过程的有效作用力增大 ,
冲击加速度增大 ,导致冲击能和冲击速度增大 ;而冲
锤提升过程中因回油背压引起的阻力也增加 ,有效
提升力大大减少 ,使冲锤加速提升时间延长 ,减速上
升行程缩短 ,导致冲击频率、冲击行程和效率均减
小. 同时 ,还可以看出 ,提高对冲击器的供油压力 ,可
以有效地改善冲击器的性能.
4) 除插装锥阀的开口量 xZ
1
过小的情况外 ,这
种冲击器的能量效率均较高 ,而且冲击能大. 由此可
知 ,即使考虑到液压控制系统的各种能量损失 ,此冲
击器的液压碎石机也是一种大冲击能 ,高效率的新
型破碎设备.
4 　结　论
a1 采用插装锥阀控制 ,可通过改变锥阀的开口
量在一定范围内实现冲击频率无级可调.
b1 冲击器的偏斜角度θ增大 ,冲击速度降低 ,
冲击能减少 ,冲击频率和能量效率增大 ,但冲击行程
变化很小 ,当θ≥45°时 ,冲击能和冲击速度急剧减
小 ,效率也有下降趋势. 但是 ,在较大偏斜角度范围
内 ,仍能保证满足破碎要求的冲击速度. 因此 ,可将
其象高频冲击器一样配置在一种多变幅机构 (如液
压挖掘机等)上进行破碎作业 ,克服了落锤式碎石机
冲击器偏斜角度很小的不足[3 ,4 ] .
c1 这种冲击器更适用于较高供油压力下工作.
通过合理匹配系统的供油压力和驱动缸的有效作用
面积比及其它有关结构参数 ,易于实现大冲击能、高
效率冲击器的设计 ,为高效低频大冲击能、频率可调
式液压碎石机冲击器的设计提供了崭新的思路.
参 　考 　文 　献
1 　朱建新 ,何清华 ,郭　勇 ,等. 一种新型液压碎石机的研制与应用.
126第 6 期　　　　　　　　　　　　　　　　　　朱建新等 : 液压缸驱动重锤式冲击器性能的理论解析
有色金属 (矿山部分) ,1998 (3) :28～31
2 　何清华 ,郭　勇 ,朱建新. 液压冲击机构研究·设计. 长沙 :中南工
业大学出版社 ,1995
3 　朱建新 ,曾桂英 ,何清华 ,等. 液压落锤式碎石机动力系统配置及
能量效率. 中南工业大学学报 ,1997 ,28 (6) :582～585
4 　朱建新 ,何清华 ,杨襄璧. 一种新型液压落锤式碎石机. 有色金属
(矿山部分) ,1993 (1) :22～25
THE THEORETICAL ANALYSIS OF HYDRO2CYLINDER2DRIVED
WEIGHT2HAMMER IMPACTOR′S PERFORMANCE
Zhu Jianxin 　He Qinghua 　Guo Yong 　Zhao Hongqiang
(College of Mechanical and Engineering , Central South University of Technology , Changsha , 410083 , China)
ABSTRACT
After analysis of the structure and work principle of hydro2cylinder2drived weight2hammer impactor , a mathematical
model was set up . In this paper , a YS250A hydraulic impactor was taken as an example. The displacement of cone insert
valve , the decline angle of impactor , the press of oil2supply system , and the valid action area ratio of drive cylinder were
utilized to analyze their effect on the performance of impactor theoretically. The result indicates that the efficiency of this
hydro2cylinder2drived weight2hammer impactor is relatively high , and it is prone to implement high impacting power , its
impacting frequency can be adjusted steplessly to a certain range. The impactor can work effectively under large decline
angle. It provides important theoretical basis for development of new type hydraulic impactor with high impacting power ,
low impacting frequency and stepless adjustment .
Key words 　hydraulic crusher ; impactor ; performance ; theoretical analysis
226 中南工业大学学报 　　　　　　　　　　　　　　　　　　　第 30 卷